Maxwellscher Dämon

Der maxwellsche Dämon oder Maxwell-Dämon ist ein vom schottischen Physiker James Clerk Maxwell 1871 veröffentlichtes Gedankenexperiment, mit dem er den Zweiten Hauptsatz der Thermodynamik in Frage stellt. Das Dilemma, das aus diesem Gedankenexperiment resultierte, wurde von vielen namhaften Physikern (z. B. Feynman) bearbeitet und führte mehrfach zu neuen Erkenntnissen. Es zeigte sich ein Zusammenhang zwischen Information und Energie, ähnlich der Beziehung zwischen Masse und Energie in Einsteins Formel $E=mc^{2}$ . Die Mindestenergie $E$ , um $n$ Bit Information zu verarbeiten, beträgt $E=nkT\ln 2$ ( $k$ ist die Boltzmann-Konstante und $T$ die absolute Temperatur des Systems). Auch heute noch inspiriert der maxwellsche Dämon die theoretische Physik. Außerhalb der Physik fand der maxwellsche Dämon aufgrund der Faszination, die dieses Dilemma auslöst, auch Eingang in die Kunst.[1]

Das Dilemma des maxwellschen Dämons

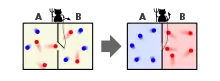
Der „Dämon“ öffnet und schließt die Klappe, um Teilchen größerer Geschwindigkeit (rot) von A nach B und solche kleinerer (blau) von B nach A durchzulassen.

Das ursprüngliche Gedankenexperiment beschreibt einen Behälter, der durch eine Trennwand geteilt wird, in der es eine kleine verschließbare Öffnung gibt. Beide Hälften enthalten Luftmoleküle; zunächst haben beide Hälften die gleiche Temperatur. Demzufolge befindet sich in beiden Hälften jeweils eine Mischung von schnellen und langsameren Molekülen, die aber beide in ihrer Verteilung derselben Temperatur entsprechen. Ein Wesen, das diese Moleküle „sehen“ kann – die Bezeichnung Dämon erhielt es erst später – öffnet und schließt die Verbindungsöffnung so, dass sich die langsamen Moleküle in der einen Hälfte des Behälters sammeln und die schnellen in der anderen. Die eine Hälfte wird damit immer kälter, die andere immer wärmer.

Unter idealen Bedingungen muss zum Öffnen und Schließen der Öffnung in der Trennwand keine Energie aufgewendet werden. Trotzdem könnte man mit der entstehenden Temperaturdifferenz, solange sie existiert, z. B. eine Wärmekraftmaschine betreiben. Man würde damit Arbeit verrichten und hätte gleichzeitig gegenüber dem Ausgangszustand im Behälter letztlich keine weitere Veränderung außer einer Abkühlung. Damit wäre der Zweite Hauptsatz der Thermodynamik verletzt („Es ist unmöglich, eine periodisch arbeitende Maschine zu konstruieren, die weiter nichts bewirkt als Hebung einer Last und Abkühlung eines Wärmereservoirs.“), und man hätte ein Perpetuum mobile zweiter Art gefunden.

Lösungsversuche

James Clerk Maxwell 1871

Maxwell selbst sah in dem von ihm geschaffenen Problem lediglich einen deutlichen Hinweis auf die Tatsache, dass der zweite Hauptsatz statistischer Natur ist, also nur im makroskopischen Bereich gilt. Wählt man die Gesamtzahl der Moleküle klein genug, wird es sogar wahrscheinlich, dass auch bei ständig geöffneter Verbindung zeitweilig deutliche Temperaturunterschiede zwischen den beiden Behälterhälften auftreten.

Lord Kelvin 1874

William Thomson, der spätere Lord Kelvin, führte die Bezeichnung „Maxwell’s demon“ ein und erkannte, dass das Kritische an dessen Beschäftigung im „Sortieren“ liegt, was sich auch auf andere Arten (vgl. Sedimentation) verwirklichen lässt. Er postulierte zusätzlich zum ursprünglichen „Temperaturdämon“ die Möglichkeit anderer Dämonen, die z. B. Wärmeenergie durch Sortieren nach der Bewegungsrichtung direkt in Bewegungsenergie verwandeln, Salzlösungen in konzentrierte Lösung und reines Wasser oder Gasgemische nach einzelnen Gasen separieren. Überall sah er in diesem Sortieren die Umkehrung des „natürlichen“ Vorganges der Dissipation.

Auch Max Planck und andere beschäftigten sich zu dieser Zeit mit dem maxwellschen Dämon. Im Allgemeinen hielt man ihn einfach für „unnatürlich“ und betrachtete das Problem damit als erledigt oder wenigstens rein akademisch. Immerhin hatte er in die gerade erst entstandene Thermodynamik noch einige Klarheit gebracht.

Aber Maxwell hatte ein tiefer greifendes Problem aufgeworfen, als man bis dahin erkannte. Mit der Dynamik der Moleküle und mit Hilfe der Statistik ließ sich zwar erklären, warum thermodynamische Prozesse spontan in ihrer „natürlichen“ Richtung ablaufen. Warum es aber nicht möglich sein sollte, solch einen Prozess mit geschicktem Einsatz technischer Mittel auch in umgekehrter Richtung zu erzwingen, war damit nicht zu erklären. Der zweite Hauptsatz, der nur ein Erfahrungssatz ist, verlangt aber genau diese Irreversibilität.

Leó Szilárd 1929

Szilárd legte 1929 eine Aufsehen erregende Habilitationsschrift Über die Entropieverminderung in einem thermodynamischen System bei Eingriffen intelligenter Wesen vor. Er vereinfachte das Modell zunächst radikal, indem er es auf ein einzelnes Molekül reduzierte. Das Wesen bringt in diesem Modell die Trennwand (die nun eher ein Kolben ist) ein, wenn das Molekül sich in einer vorher festgelegten Hälfte des Behälters befindet. Das Molekül drückt nun die Kolbentrennwand nach außen und verrichtet dabei Arbeit an einer Masse. Dabei wird Wärme aus der Umgebung aufgenommen, so dass die Temperatur gleich bleibt. Dann wiederholt sich der Zyklus. Mit jedem Zyklus verringert sich die Wärme der Umgebung, während die potenzielle Energie der Masse sich um denselben Betrag vergrößert. Andererseits muss für jeden Zyklus das Wesen zunächst eine Messung vornehmen, indem es eine Hälfte des Behälters beobachtet: Ist das Molekül darin oder nicht? Durch die Messung wird also eine binäre Information gewonnen. Diese Information muss zumindest kurzfristig in einem Gedächtnis festgehalten werden.

Die Angelegenheit war jetzt überschaubar. Die einzige Interaktion des Wesens mit dem Ein-Molekül-Gas ist die Messung. Die thermodynamische Entropieverringerung kann, damit der Zweite Hauptsatz nicht verletzt wird, also nur durch eine Entropieerzeugung von gleichem Betrag durch die Messung ausgeglichen werden. Den Betrag dieser Entropie $S$ berechnete Szilárd aus den thermodynamischen Vorgängen zu $S=k\cdot \ln 2$ , mit der Boltzmann-Konstante $k$ .

Das bedeutet, dass die mit der Messung gespeicherte Information in irgendeiner Form diese Entropie $S=k\cdot \ln 2$ beinhalten musste. Damit war zum ersten Mal, wenn auch noch recht unscharf, von einer Entropie der Information die Rede. Der maxwellsche Dämon hatte zur Grundlage der Informationstheorie beigetragen. Wo im System aus Messung, Information und Speicher die Entropie genau zu suchen ist, konnte Szilárd noch nicht festlegen.

Léon Brillouin 1951

Brillouin fragte 1951 genauer nach der Messung, dem „Sehen“ des Dämons. Sehen im wörtlichen Sinn bedeutet letztlich eine Abtastung der Moleküle mit Licht, auch wenn ganz andere Wellenlängen denkbar sind. Diese Abtastung bedeutet bei Berücksichtigung der Quantennatur des Lichts die Wechselwirkung zweier Teilchen, eines Moleküls und eines Photons, durch Stoß. Brillouin konnte nun relativ einfach zeigen, dass bei diesem Stoß immer genügend Entropie frei wird, um den Zweiten Hauptsatz einzuhalten, wenn vorausgesetzt wird, dass die Energie der Photonen groß genug sein muss, um dem Dämon überhaupt Information liefern zu können. Der Dämon schien erledigt, die bei Szilárd noch offene Frage nach dem genauen Ort der Entropieerzeugung auf unspektakuläre Weise geklärt.

Brillouin ging in seiner Interpretation aber weiter, er sah die Photonen als Übermittler von („gebundener“) Information und postulierte erstmals einen direkten Zusammenhang zwischen der 1948 von Shannon eingeführten Entropie der Information und thermodynamischer Entropie, wozu er Shannons Entropie mit einer Konstanten multiplizierte. Er formulierte dann das „Negentropie-Prinzip der Information“, das umstritten blieb: Die Information selbst ist negative Entropie (Negentropie) und bewirkt im Sinne einer Erhaltung eine entsprechende Entropieerhöhung im Gas. Der Dämon kann diese anschließend höchstens gerade wieder ausgleichen.

Allerdings erwies sich die Voraussetzung der Messung mit Photonen als zu starke Einschränkung, die auch umgangen werden konnte.

Rolf Landauer und Charles Bennett 1961/1982

Landauer beschäftigte sich nicht mit dem maxwellschen Dämon, sondern mit Informationsspeicherung. Er konnte 1961 am Modell eines Potenzialtopfs zeigen, dass das Löschen – im Sinne des Zurücksetzens in einen wiederbeschreibbaren Zustand – eines Bits physikalisch gespeicherter Information immer die bereits bekannte Entropie $k\,\ln 2$ freisetzen muss, heute als Landauer-Prinzip bekannt. Er stellte einen Zusammenhang zur logischen Irreversibilität der Löschoperation her. Logisch reversible Operationen wie Schreiben und Lesen bewirken dagegen keine Entropie- oder Energiefreisetzung. Damit war für das, was Brillouin physikalisch irrelevant „freie“ Information genannt hatte, ein physikalischer Zusammenhang nachgewiesen. Aber erst Charles Bennett zeigte 1982, dass mit der Anwendung des Landauer-Prinzips auf das Gedächtnis des maxwellschen Dämons dem Gas exakt die vermisste Entropie wieder zugeführt wird, um den Zweiten Hauptsatz zu erfüllen, während andererseits die Messung mit beliebig geringer Dissipation ausgeführt werden kann. Gemäß Bennett muss die Schwingtür des Maxwellschen Schwingtüren-Dämons zwangsweise schwingen, nachdem ein Gaspartikel die Tür passiert hat. So wie die geschlossene Tür den Durchtritt eines Gaspartikels in die augenscheinlich „richtige“ Richtung bewirkt, bewirkt die schwingende Tür den Durchtritt eines Gaspartikels in die Gegenrichtung. Die schwingende Tür stellt einen Zustand lokaler Überhitzung dar. Die überschüssige Energie gibt diese vorzugsweise durch Beschleunigung des Gaspartikels in die Gegenrichtung ab. Der Anteil geschlossener Türen zu schwingenden Türen ist unabhängig von der Gasdichte (Boltzmann-Statistik).

Orly R. Shenker sieht in einer detaillierten Analyse von Landauers Thesen aus dem Jahr 2000 diverse Fehler in der Argumentation Landauers, die sich insbesondere auf eine unzulässige Gleichsetzung der Dissipationsbegriffe der Informationstheorie und der Thermodynamik zurückführen ließen. Sie weist darauf hin, dass das Landauer-Prinzip auf dem Zweiten Hauptsatz der Thermodynamik aufbaut. Da durch die Lösung des Problems des maxwellschen Dämons die Gültigkeit des Zweiten Hauptsatzes bewiesen werden soll, entstehe ein unzulässiger Zirkelbezug. Bennett und Landauer widerlegen also den Maxwellschen Dämon nicht, in dem Sinne, dass sie die Gültigkeit des Zweiten Hauptsatzes auch für den Maxwellschen Dämon beweisen, sondern sie zeigen, wo genau der Maxwellsche Dämon gegen den Zweiten Hauptsatz verstößt.

Oliver Penrose 1970

Penrose beschäftigte sich im Jahr 1970 mit dem maxwellschen Dämon und kam, ohne Landauers Arbeit zu kennen, noch vor Bennett mit einer statistischen Argumentation zur Entropie zum gleichen Ergebnis: Wenn der Speicher des Dämons voll ist, kann er erst nach Zurücksetzung weiter benutzt werden. Dies verringert die möglichen Zustände des Gesamtsystems. Die Anwendung einer statistischen Entropiedefinition auf den Speicher führt dann ebenfalls zu Landauers Ergebnis.

Siehe auch

Literatur

Charles H. Bennett: Maxwells Dämon Spektrum der Wissenschaft, Januar 1988, S. 48.
James Clerk Maxwell: Theory of Heat. 1871
Harvey S. Leff (Hrsg.), Andrew F. Rex (Hrsg.): Maxwell’s Demon 2: Entropy, Classical and Quantum Information, Computing. Institute of Physics Publishing, Bristol 2003, ISBN 0-7503-0759-5

Weblinks

Commons: Maxwell's demon – Sammlung von Bildern, Videos und Audiodateien

Orly R. Shenker: Logic and Entropy. (2000)

Einzelnachweise

z. B. in den Roman Homo faber von Max Frisch

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] z. B. in den Roman Homo faber von Max Frisch