Phasenübergang
Ein Phasenübergang bzw. eine Phasenumwandlung oder Phasentransformation ist in der Thermodynamik die Umwandlung einer oder mehrerer Phasen eines Stoffes in andere Phasen. Eine grafische Darstellung der Stabilitätsbereiche der Phasen in Abhängigkeit von den Zustandsvariablen wie Druck, Temperatur, chemischer Zusammensetzung und magnetischer Feldstärke liefern Phasendiagramme. In diesen Diagrammen sind die Stabilitätsbereiche durch Phasengrenzlinien begrenzt, an denen die Phasenübergänge ablaufen.
Klassifikation
Phasenübergänge können u. a. zwischen festen, flüssigen und gasförmigen Phasen auftreten. Für Phasenübergänge zwischen bestimmten Aggregatzuständen (also sogenannten Aggregatzustandsänderungen) gibt es spezielle Bezeichnungen:[1]
- Schmelzen (Übergang von fest zu flüssig)
- Erstarren, auch Gefrieren oder Kristallisieren (Übergang von flüssig zu fest)
- Verdampfen (Übergang von flüssig zu gasförmig)
- Kondensieren (Übergang von gasförmig zu flüssig)
- Sublimieren (Übergang von fest zu gasförmig)
- Resublimation (Übergang von gasförmig zu fest), siehe dazu auch Resublimieren
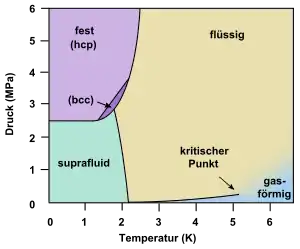
In einigen Stoffsystemen verschwinden oberhalb eines kritischen Punktes, der durch eine kritische Temperatur und einen kritischen Druck gekennzeichnet ist, die Phasengrenzflächen zwischen flüssiger und gasförmiger Phase. Damit sind Flüssigkeit und Gas unter diesen Bedingungen nur noch eine Phase, die „überkritisch“ genannt wird. Somit kann es dort auch kein Verdampfen und Kondensieren mehr geben.
Ebenso kann es in einigen Stoffsystemen einen Tripelpunkt geben, an dem sowohl eine feste als auch eine flüssige und eine gasförmige Phase im Gleichgewicht miteinander stehen und dementsprechend alle sechs erstgenannten Formen des Phasenübergangs gleichzeitig ablaufen.
Andere Typen von Phasenübergängen werden im Weiteren erwähnt.
Klassifikation nach Ehrenfest
Grundsätzlich werden Phasenübergänge nach der Ehrenfest-Klassifikation (nach Paul Ehrenfest) in unterschiedliche Ordnungen eingeteilt. Dazu betrachtet man thermodynamische Größen wie Volumen, Enthalpie oder Entropie in Abhängigkeit von einer (oder mehreren) Variablen, meist der Temperatur. Das System wird durch ein thermodynamisches Potential G (Gibbs-Energie, freie Enthalpie) beschrieben. Bei einem Phasenübergang n-ter Ordnung ist G als Funktion z. B. der Temperatur (oder des Drucks) betrachtet samt seinen ersten n-1 Ableitungen stetig, erst die n-te Ableitung ist unstetig.[2]
Genauer werden Phasenübergänge in der Landau-Theorie beschrieben, wo die Phasen als Folge von Symmetriebrüchen von ungeordneten Phasen zu geordneten Phasen mit gleichzeitiger Erscheinung eines neuen Ordnungsparameters übergehen. Diese sind von begleitenden Sprüngen makroskopischer Größen wie der Magnetisierung oder der Deformation eines Kristallgitters gekennzeichnet.
Von besonderer Bedeutung ist die Unterscheidung in Phasenübergänge erster Ordnung und solche höherer Ordnung (Kontinuierliche Phasenübergänge), speziell zweiter Ordnung. In der modernen Klassifikation wird in der Tat nur diese Unterscheidung vorgenommen:
- Ein Beispiel für einen Phasenübergang erster Ordnung ist der Übergang einer Flüssigkeit wie Wasser zu einem Feststoff am Gefrierpunkt. Zur Überführung vom festen in den flüssigen Zustand muss zusätzlich Wärmeenergie (in Form von latenter Wärme) zugeführt werden, ohne dass es zu einer tatsächlichen Temperaturerhöhung kommt. Da es dabei zu einer Unstetigkeit in der Entropie (der ersten Ableitung der freien Enthalpie G nach der Temperatur) kommt, ist das Schmelzen von Eis ein Phasenübergang erster Ordnung. Ebenso macht das Volumen (erste Ableitung von G nach dem Druck p) einen Sprung an der Phasengrenze; der resultierende Dichteunterschied der Phasen entspricht hier dem Ordnungsparameter in der Landautheorie. Ein Sprung im Ordnungsparameter ist typisch für Phasenübergänge erster Art.
- Ein Beispiel für einen Phasenübergang zweiter Ordnung oder auch kontinuierlichen Phasenübergang ist der Übergang von der ferromagnetischen zur paramagnetischen Phase bei der Curie-Temperatur in einem Ferromagneten. Der Ordnungsparameter ist die Magnetisierung, die am Phasenübergang stetig gegen Null geht, ohne dass dabei zusätzlich latente Wärme auftritt. Jedoch tritt in der zweiten Ableitung der freien Enthalpie nach der Temperatur ein Sprung auf (Wärmekapazität). Dieses Verhalten kennzeichnet einen Phasenübergang zweiter Ordnung. Typisch ist hier ein stetiger Übergang im Ordnungsparameter. Ein weiteres Beispiel für einen Phasenübergang zweiter Ordnung ist der Übergang von Normalmetall zu Supraleiter.
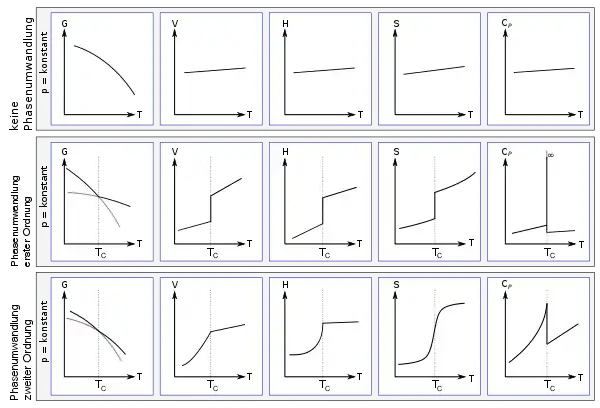
In der folgenden Abbildung sind die erwähnten Phasenübergänge erster und zweiter Ordnung nach Ehrenfest dargestellt. Die Abbildung zeigt bei konstantem Druck die freie Enthalpie G, das Volumen V, die Enthalpie H, die Entropie S und die Wärmekapazität CP, jeweils in Abhängigkeit von der Temperatur. In der obersten Reihe sind die Parameter ohne Phasenübergang gezeigt, in der Mitte ein Phasenübergang erster Ordnung und in der unteren Reihe ein Phasenübergang zweiter Ordnung. Die Phasenumwandlung findet jeweils bei der kritischen Temperatur TC statt. In der Abbildung sind die Kurven der freien Enthalpie der jeweiligen Phase eingezeichnet und grau in der jeweils anderen Phase fortgesetzt; sie können dort Unterkühlungseffekte oder Metastabilität vorhersagen.
Weitere Klassifikationen
Neben dieser grundsätzlichen Einteilung gibt es noch eine Reihe weiterer Unterscheidungen in speziellen Anwendungsgebieten.
Strukturelle Klassifikation
Nach der strukturellen Klassifikation unterscheidet man in der Mineralogie:
- diskontinuierliche Phasenübergänge, charakterisiert durch den Bruch chemischer Bindungen. Ein Beispiel ist die Umwandlung von Graphit in Diamant.
- martensitische Phasenübergänge, bei denen das Kristallgitter geschert wird. Ein Beispiel ist die Umwandlung von γ- zu α-Eisen.
Martensitische Phasenübergänge werden nochmals gegliedert in:- athermale Phasenübergänge (Umwandlungsgrad nicht zeitabhängig)
- isothermale Phasenübergänge (Umwandlungsgrad zeitabhängig).
- Kontinuierliche Phasenübergänge sind nur mit einer Ordnung der Kristallstruktur verbunden.
Man unterscheidet zwei Subtypen:- Displazive Phasenübergänge, bei denen es zu einer Verschiebung oder Rotation der Atompositionen kommt (z. B. bei der Umwandlung von Hochquarz in Tiefquarz).
- Ordnungs-Unordnungs-Phasenübergänge, bei denen es zu einer Ordnung mehrerer auf verschiedene Atompositionen statistisch verteilter Atome kommt, sodass jede Position nur noch mit einer Atomsorte besetzt ist.
- In beiden Fällen kann es zum Auftreten großräumiger Periodizitäten kommen, welche die Gitterstruktur überlagern. Man bezeichnet diese als inkommensurable Strukturen.
Kinetische Klassifikation
Die kinetische Klassifikation unterteilt Phasenübergänge nach ihrer Reaktionsgeschwindigkeit in:
- Phasenübergänge nullter Ordnung, bei denen die Reaktionsgeschwindigkeit konstant ist
- Phasenübergänge erster Ordnung, bei denen die Reaktionsgeschwindigkeit von der Konzentration einer Ausgangsphase abhängt
- Phasenübergänge zweiter Ordnung, bei denen die Reaktionsgeschwindigkeit von den Konzentrationen zweier Ausgangssubstanzen abhängt usw.
Strömungsdynamische Klassifikation
Strömungsdynamisch wird unterschieden bei Geschwindigkeits-Übergängen, wo sich Strömungseigenschaften schlagartig und massiv ändern, z. B. die Änderung wichtiger Werte wie Widerstand und Auftrieb bei Gasen und Flüssigkeiten. Ein wichtiger Bereich ist der kritische Übergang von unterkritisch zu überkritisch (siehe Reynoldszahl, laminare Strömung, turbulente Strömung).
Beispiele
Phasenübergänge sind oft mit der Änderung bestimmter Materialeigenschaften verbunden, zum Beispiel:
- Wechsel der Kristallstruktur (struktureller Phasenübergang) oder auch der Adsorbatstruktur.
- Wechsel zwischen ferro- und paramagnetischem Verhalten bei der kritischen oder Curie-Temperatur
- Wechsel zwischen verschiedenen magnetischen Ordnungen, z. B. von kommensurabler zu inkommensurabler Magnetstruktur
- Wechsel zwischen ferro- und dielektrischem Verhalten
- in der Hochenergiephysik: Entstehung von Quark-Gluon-Plasma bei hohen Temperaturen und Drücken
- Übergang zur Superfluidität
- Übergang zur Supraleitung
- Übergang von unterkritischer Strömung zu überkritisch (Strömungsdynamik).
- Übergang von einer glatten zu einer atomar aufgerauten Kristalloberfläche (Facettierung)[3]
Theorie
Die Theorie kontinuierlicher Phasenübergänge geht von einem Ordnungsparameter aus (z. B. der Magnetisierung bei der Umwandlung eines Ferromagneten in einen Paramagneten). Bei kontinuierlichen Phasenübergängen geht der Ordnungsparameter bei Annäherung an den Umwandlungspunkt kontinuierlich gegen Null (dagegen springt er an einem Phasenübergang erster Ordnung), und die Korrelationslänge divergiert (bei einer Umwandlung erster Ordnung bleibt sie endlich).
Sehr unterschiedliche Arten kontinuierlicher Phasenübergänge lassen sich in Universalitätsklassen zusammenfassen, was letztlich erneut auf die Divergenz der Korrelationslänge zurückzuführen ist. Diese Klassen können durch einige wenige Parameter charakterisiert werden, beispielsweise durch einen kritischen Exponenten. Dies ist der Exponent eines Potenzgesetzes, das beschreibt, wie ein Ordnungsparameter in der Nähe des kritischen Punktes verschwindet, z. B. als Funktion des Abstandes der Temperatur vom kritischen Punkt.
Der Zusammenhang zwischen grundlegenden Symmetrien der jeweiligen Phasen und den Werten dieser Parameter ist im Rahmen der Statistischen Physik in den letzten Dekaden ausführlich theoretisch untersucht und auch in einer Vielzahl von Experimenten sowie in Computersimulationen überprüft worden.
Bei theoretischen Beschreibungen von Phasenübergängen wird mitunter die Landau- oder Mean-Field-Theorie benutzt. Dabei werden jedoch kritische thermische Fluktuationen vernachlässigt, die in der Umgebung des Übergangs eine wesentliche Rolle spielen können (und beispielsweise in der kritischen Opaleszenz beobachtet werden). Die Landau-Theorie kann trotzdem als Ausgangspunkt genauerer Theorien (von der Skalentheorie von Pokrowski und Patashinski bis hin zur epsilon-Entwicklung von K.G. Wilson und M.E. Fisher) wertvolle erste Einsichten vermitteln.
Dies ist insbesondere von Kenneth G. Wilson erkannt worden, der 1982 den Nobelpreis für bahnbrechende Arbeiten über kontinuierliche Phasenübergänge erhielt. Wilson ist einer der entscheidenden Pioniere der Renormierungsgruppentheorie, die berücksichtigt, dass bei kontinuierlichen Phasenübergängen die kritischen Fluktuationen auf vielen Längenskalen in selbstähnlicher Form stattfinden. Analoge Theorien werden heute in vielen Bereichen der Physik und Mathematik angewendet.
Bedeutung für die Mineralogie
Das Wissen über die physikochemischen Bedingungen, bei denen Phasenübergänge ablaufen, erlaubt Mineralogen Rückschlüsse über die Entstehungsgeschichte von Gesteinen. Wenn ein Gestein unter hohe Drücke und Temperaturen gerät, kommt es in vielen Fällen zu einer Phasenumwandlung. Unter der Voraussetzung, dass die anschließende Abkühlung so rasch erfolgt, dass die Umkehrreaktion aufgrund der bei tiefen Temperaturen kaum noch möglichen Diffusion nicht mehr stattfindet, kann man davon ausgehen, dass die bei hohen Temperaturen und Drücken stabilen Minerale „eingefroren“ werden und so an der Erdoberfläche erhalten bleiben. So sind Aussagen darüber möglich, welche Temperaturen und Drücke ein Gestein im Laufe seiner Genese „gesehen“ hat. Beispiele hierfür sind die Phasenübergänge zwischen Andalusit, Sillimanit und Disthen im Bereich der Aluminosilikate, die Umwandlung von Graphit in Diamant und von Quarz in Coesit oder Stishovit. Das durch experimentelle Mineralogie erworbene Wissen über Phasenübergänge erklärt auch das rheologische Verhalten des Erdmantels: Das Eisen-Magnesiumsilikat Olivin wandelt sich in 410 km Tiefe in den in der β-Spinell-Struktur kristallisierenden Wadsleyit um, der sich seinerseits in 520 km Tiefe weiter in den in der γ-Spinell-Struktur auftretenden Ringwoodit umwandelt (siehe auch die Artikel 410-km-Diskontinuität und 520-km-Diskontinuität). Dabei kommt es zu keinerlei chemischen Veränderungen, sondern nur zu einer Änderung der Kristallstruktur. Am Beispiel der Umwandlung von Coesit in Stishovit kann man gut erklären, warum es zu einer Phasenumwandlung kommt: Unter normalen Bedingungen ist Silizium von vier Sauerstoffatomen umgeben, unter hohen Drücken rücken die Atome jedoch dichter zusammen, so dass die Koordination durch sechs Sauerstoffatome energetisch günstiger ist.
Bedeutung für technische Prozesse
Während des keramischen Brandes wandelt sich bei einer Temperatur von 573 °C Quarz in Hochquarz um. Dabei ändert sich das Volumen. Bei einer zu großen Heizrate kann dies zum Zerspringen der Keramik führen. Deshalb wird die Heizrate in diesem Temperaturbereich gedrosselt.
Im Bereich der Konservierung von Kunstobjekten werden die Gegenstände oft kühl und trocken gelagert und auch ausgestellt. Bei Objekten aus Zinn ist dies nicht richtig, weil dieses unterhalb von 15 °C in eine andere Modifikation übergeht, deren äußeres Erscheinungsbild wenig attraktiv ist und die als Zinnpest bezeichnet wird.
Für die Kunstgeschichte ist es interessant zu wissen, dass früher oft das Blaupigment Azurit für die Darstellung des Himmels verwendet wurde. Im Lauf der Jahrhunderte ist dieses jedoch in die thermodynamisch stabile Form Malachit umgewandelt worden, welche grün ist. Dadurch ist der Himmel auf alten Bildern manchmal grün.
Bei der Stahlerzeugung sind mit der Umwandlung der Eisenmodifikation von Austenit in Ferrit bzw. Martensit Veränderungen des Gefüges verbunden, die für die Eigenschaften des Stahls von großer Bedeutung sind.
In zweidimensionalen Materialien, z. B. in dünnen magnetischen Schichten, kann es nur unter eingeschränkten Bedingungen langreichweitige Ordnung und damit einen Phasenübergang geben. Dieser interessante Aspekt wird im Mermin-Wagner-Theorem (nach N. David Mermin und Herbert Wagner) behandelt und ist auch experimentell untersucht worden.
Paraffine besitzen eine besonders große Volumenänderung um etwa 30 % beim Phasenübergang von fest nach flüssig. Dieser Hub kann für die Konstruktion von Aktoren genutzt werden.
Messmethoden
Für die Messungen von Phasenübergangen werden eine Reihe von Methoden eingesetzt, wie z. B.:
- Dynamische Differenzkalorimetrie
- Dielektrische Spektroskopie
- Dynamisch-mechanische Analyse
- Polarisationsmikroskopie
- Röntgenbeugung, Neutronenbeugung (z. B. Hoch- und Tieftemperaturpulverdiffraktometrie)
- Raman-Spektroskopie
- UV/VIS-Spektroskopie
- SQUID (Messung von magnetischen Übergängen)
- Halleffekt (Messung von magnetischen Übergängen)
- Mößbauer-Spektroskopie (Gleichzeitige Messung von magnetischen und nicht-magnetischen Übergängen. Bis max. ca. 800–1000 °C)
- Gestörte Gamma-Gamma-Winkelkorrelation (Gleichzeitige Messung von magnetischen und nicht-magnetischen Übergängen. Unbegrenzter Temperaturbereich, bis über 2000 °C erprobt, theoretisch bis zum höchstschmelzenden Festkörper Tantalhafniumcarbid mit 4215 °C.)
Siehe auch
Literatur
- H. E. Stanley: Introduction to Phase Transitions and Critical Phenomena. Oxford University Press, 1971.
- W. Gebhard, U. Krey: Phasenübergänge und kritische Phänomene. Vieweg, 1980.
- C. Domb, M. S. Green, J. L. Lebowitz (Hrsg.): Phase Transitions and Critical Phenomena. Band 1–20 (1972–2001). Academic Press.
- M. E. Fisher: Renormalization Group in Theory of Critical Behavior. In: Reviews of Modern Physics. Band 46, 1974, S. 597–616.
- Mats Hillert: Phase equilibria, phase diagrams and phase transformations – their thermodynamic basis. Cambridge University Press, Cambridge 2008, ISBN 0-521-85351-6.
- Pierre Papon u. a.: The physics of phase transitions – concepts and applications. Springer, Berlin 2006, ISBN 3-540-33389-4.
- Vadim V. Brazhkin: New kinds of phase transitions – transformations in disordered substances. Kluwer Academic, Dordrecht 2002, ISBN 1-4020-0825-2.
Einzelnachweise
- Hans-Dieter Jakubke, Ruth Karcher (Koordinatoren): Lexikon der Chemie in drei Bänden, Spektrum Verlag, Heidelberg, Band 3, 1999, ISBN 3-8274-0381-2, S. 11–12.
- W. Dieterich: Theorie der Phasenübergänge. (PDF; 1,1 MB) Skript, Universität Konstanz, S. 5.
- Govindhan Dhanaraj, Kullaiah Byrappa, Vishwanath Prasad, Michael Dudley (Hrsg.): Springer Handbook of Crystal Growth. [Elektronische Ressource]. Springer, Heidelberg 2010, ISBN 978-3-540-74761-1, S. 191 (eingeschränkte Vorschau in der Google-Buchsuche).