Tripelpunkt

In der Thermodynamik ist ein Tripelpunkt (auch Dreiphasenpunkt) ein Zustand eines aus einer einzigen Stoffkomponente bestehenden Systems, in dem Temperatur und Druck dreier Phasen im thermodynamischen Gleichgewicht stehen.[1]

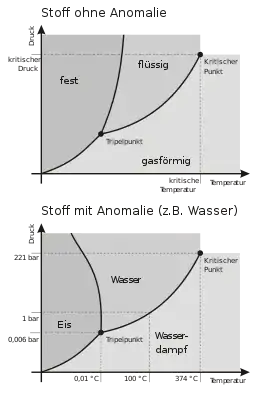
Phasendiagramm eines „gewöhnlichen“ Stoffes und des Wassers, jeweils mit Darstellung des Tripelpunktes und des Kritischen Punkts.

Die beteiligten Phasen können die drei Aggregatzustände des Stoffes darstellen, aber auch verschiedene Modifikationen der festen oder der flüssigen Phase; ein Beispiel hierfür sind die verschiedenen möglichen Kristallstrukturen des Wassereises. An Tripelpunkten können je nach Stoff also eine feste, eine flüssige und eine dampfförmige Phase koexistieren, aber auch zwei feste Phasen und eine flüssige, oder zwei feste und eine dampfförmige, oder drei feste, in seltenen Fällen auch zwei flüssige[2] und eine dampfförmige.

In einem Druck-Temperatur-Diagramm (kurz p-T-Diagramm) wird ein Tripelpunkts-Zustand als ein Punkt dargestellt. Handelt es sich insbesondere um ein p-T-Phasendiagramm und bei den drei koexistierenden Phasen um die drei verschiedenen Aggregatzustände, dann ist der Tripelpunkt der Schnittpunkt der beiden Phasengrenzlinien Sättigungsdampfdruck und Schmelzkurve: Auf der Sättigungsdampfdruckkurve stehen die flüssige und die dampfförmige Phase im Gleichgewicht, auf der Schmelzkurve die flüssige und die feste Phase, am Schnittpunkt beider Kurven alle drei.

Anzahl der Tripelpunkte

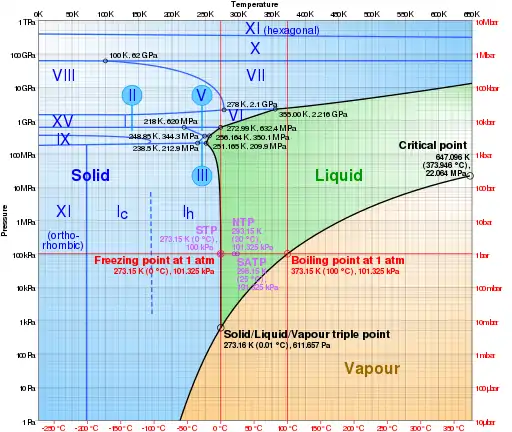
Gibt es $p$ mögliche Phasen im System, dann besitzt es $\textstyle {\frac {p!}{(p-3)!3!}}$ Tripelpunkte.[1] Schwefel beispielsweise kann in vier Phasen vorliegen: einer dampfförmigen, einer flüssigen und zwei festen (einer mit rhombischem und einer mit monoklinem Kristallgitter). Im Phasendiagramm des Schwefels existieren daher vier Tripelpunkte.[1] Hätte Wasser nur die drei Phasen fest, flüssig und dampfförmig, dann besäße es genau einen Tripelpunkt. Aufgrund der Existenz verschiedener Eis-Modifikationen gibt es weitere Tripelpunkte.

Tripelpunkt und Gibbssche Phasenregel

Ein Tripelpunkt stellt einen Spezialfall der Gibbsschen Phasenregel dar:

f=N-P+2

Der Freiheitsgrad ${\textstyle f}$ des Systems (hier eines Einkomponentensystems: ${\textstyle N=1}$ , mit drei Phasen: ${\textstyle P=3}$ ) ist in Tripelpunkten nach der Phasenregel immer ${\textstyle f=0}$ : Verändert man eine intensive Zustandsgröße, wird sofort das Gleichgewicht der Phasen verlassen. Dies ist auch der Grund dafür, dass es in einem einkomponentigen System keine 4 Phasengrenzlinien geben kann, die sich in einem Punkt treffen (hier wäre ${\textstyle f=-1}$ ).

Beispiel: Tripelpunkt des Wassers

Der Tripelpunkt des Wassers ist jener Punkt im p-T-Diagramm des Wassers, in dem die drei Phasen reines flüssiges Wasser, reines Wassereis und Wasserdampf im Gleichgewicht stehen.[3] Dabei ist der allen drei Phasen gemeinsame Druck gleich dem Sättigungsdampfdruck des reinen Wassers bei der allen drei Phasen gemeinsamen Temperatur.

Dieser Druck beträgt gemäß dem international akzeptierten Bestwert von Guildner, Johnson und Jones 611,657 (± 0,010) Pa (ca. 6 mbar).[4][5]

Die Tripelpunktstemperatur betrug bis zum 19. Mai 2019 – als definierender Fixpunkt der Temperaturskala – exakt 273,16 K (oder 0,01 °C).[6] Seit der Neudefinition der SI-Einheiten 2019 ist die Temperaturskala unabhängig vom Wasser definiert,[7] sodass die Tripelpunktstemperatur wieder mit einer gewissen Messunsicherheit experimentell bestimmt werden muss. Diese Unsicherheit betrug bei Einführung der Neudefinition 100 µK,[8][9] innerhalb dieser Unsicherheit ist der Zahlenwert nach wie vor 273,16 K.

Sind die drei Phasen in einem Behälter (etwa in einer Tripelpunktzelle) ins Gleichgewicht gebracht, bleiben Tripelpunktstemperatur und Tripelpunktsdruck längere Zeit erhalten, auch wenn ein geringer Wärmestrom durch die nicht perfekt isolierende Wand des Behälters fließt. Wie bei allen Phasenübergängen des Wassers wird der Zu- oder Abstrom von Wärme durch entsprechenden Latentwärmeumsatz kompensiert, indem sich das Mengenverhältnis der Phasen durch Schmelz-, Gefrier-, Verdunstungs-, Kondensations- oder Sublimationsvorgänge entsprechend verschiebt. Druck und Temperatur bleiben konstant, bis eine der Phasen aufgezehrt ist. Wegen dieser Eigenschaft und des genau definierten Tripelpunkts eignet sich eine solche Tripelpunktzelle für Kalibrierzwecke.

Neben dem hier beschriebenen Koexistenzpunkt von flüssigem, gefrorenem und dampfförmigem Wasser gibt es im Phasendiagramm des Wassers noch weitere aber weniger bedeutende Tripelpunkte, an denen zwei oder drei verschiedene Eismodifikationen beteiligt sind (siehe die Tabelle weiter unten).

Tripelgebiet

Im dreidimensionalen Phasendiagramm des Wassers bewegt sich das System entlang der Tripellinie, wenn sein Volumen verändert wird, während es Tripelpunktsdruck und Tripelpunktstemperatur besitzt.

Der Tripelpunkt ist, wie beschrieben, ein Punkt im p-T-Diagramm, so dass Druck und Temperatur eines im Tripelpunkt befindlichen Systems eindeutig bestimmt sind. Dennoch kann das System, wenn es sich in diesem Punkt befindet, verschiedene Gleichgewichtszustände einnehmen – solange dabei keine der Phasen ganz verschwindet. Das System kann etwa Wärme mit der Umgebung austauschen, und sein Volumen kann sich ändern; dabei ändern sich die relativen Anteile der drei Phasen. Als Zustandskoordinaten sind hier die extensiven Koordinaten inneren Energie und Gesamtvolumen brauchbar. Im U-V-Diagramm füllen die Zustände der gleichzeitigen Koexistenz der drei Phasen ein zwei-dimensionales Gebiet aus, während Druck und Temperatur hier zu einem konstanten Wert entartet sind.[10] Neben der Erkennbarkeit ist es gerade diese Unempfindlichkeit gegenüber kleinen Schwankungen des Volumens und der Wärme Zu- und Abfuhr, die den Tripelpunkt zur Nutzung für eine Temperaturreferenz auszeichnet.

Bei einer Darstellung der Gleichgewichtszustände als Fläche in einem Druck-Volumen-Temperatur-Raum, siehe Grafik, schrumpft das Tripelgebiet zu einer eindimensionalen Linie, der Tripellinie, die durch die konstanten Tripelpunktswerte für Druck und Temperatur gekennzeichnet ist. Entlang der Tripellinie korrespondieren verschiedene Volumenwerte mit Änderungen der Mengenanteile der Phasen.

Die Variabilität der extensiven Größen Volumen und innere Energie widerspricht nicht der Gibbsschen Phasenregel, da diese Regel nur Aussagen über intensive Variablen macht.

Skalenfixpunkte und andere Werte

Die Eindeutigkeit des Tripelpunkts liefert besonders gute Temperatur-Fixpunkte für die Kalibrierung der Skalen von Thermometern.

Gängige Tripelpunkt-Temperaturangaben, z. B. nach der Internationalen Temperaturskala von 1990, sind:

Wasser: 273,16 K (0,01 °C) bei 611,657 ± 0,010 Pa
Quecksilber: ITS-90-Fixpunkt 234,3156 K (−38,8344 °C) bei 1,65 · 10⁻⁴ Pa

Weitere Temperaturen für Tripelpunkte liefert die ITS-90.

Hochdruckphasendiagramm von Wasser mit weiteren Tripelpunkten verschiedener fester Phasen

Tripelpunkte einiger Stoffe[11]
Stoff		Temperatur		Druck
Name	Summenformel	K	°C	kPa
Wasser	H₂O	273,16	−000,01	000,611657
Sauerstoff	O₂	054,361	−218,789	000,14633
Kohlendioxid	CO₂	216,592	0−56,558	517,95
Stickstoff	N₂	063,151	−209,999	012,523
Ammoniak	NH₃	195,5	0−77,65	006,1

Tripelpunkte von Wasser
beteiligte Phasen	Temperatur	Druck (MPa)
flüssiges Wasser, Eis I_h, Wasserdampf	−00,01 °C	000,000 611 657
flüssiges Wasser, Eis I_h, Eis III	−22 °C	209,9
flüssiges Wasser, Eis III, Eis V	−17 °C	350,1
flüssiges Wasser, Eis V, Eis VI	−00,16 °C	632,4
Eis I_h, Eis II, Eis III	−35 °C	213
Eis II, Eis III, Eis V	−24 °C	344
Eis II, Eis V, Eis VI	−70 °C	626

Höhere Zustände ohne Freiheitsgrad

Wie die Phasenregel zeigt, hat ein Zustand eines einkomponentigen Systems, in dem drei Phasen im Gleichgewicht existieren, keine verbleibenden Freiheitsgrade (er ist ein „invarianter“ oder „nonvarianter“ Zustand), und es können in einem solchen System nicht mehr als drei Phasen koexistieren. Aus der Phasenregel folgt aber auch, dass in Systemen, die aus mehreren unabhängigen Komponenten bestehen, mehr als drei Phasen an invarianten Punkten im Gleichgewicht stehen können.

Quadrupelpunkt

Kann ein aus zwei unabhängigen Komponenten bestehendes System in vier verschiedene Phasen zerfallen, dann ist ein Zustand, in dem alle vier Phasen im Gleichgewicht stehen, ein invarianter Zustand.[12] Ein Beispiel[13] für einen solchen Quadrupelpunkt ist der eutektische Punkt eines binären Systems mit den im Gleichgewicht stehenden

beiden festen Phasen,
einer flüssigen Phase und
einer gasförmigen Phase.

Quintupelpunkt

Kann ein aus drei unabhängigen Komponenten bestehendes System in fünf verschiedene Phasen zerfallen, dann ist ein Zustand, in dem alle fünf Phasen im Gleichgewicht stehen, ein invarianter Zustand.[14] Ein Beispiel[14] ist ein System, das aus den drei Komponenten

Wasser, H₂O
Natriumsulfat, Na₂SO₄
Magnesiumsulfat, MgSO₄

besteht. Bei einer Temperatur von 22 °C können die folgenden fünf Phasen koexistieren:

Wasserdampf
eine flüssige Mischung aus Wasser, Natriumsulfat und Magnesiumsulfat
Kristalle von Natriumsulfat-Decahydrat, Na₂SO₄·10 H₂O
Kristalle von Magnesiumsulfat-Decahydrat, MgSO₄·10 H₂O
Kristalle von Natriummagnesiumsulfat-Tetrahydrat, Na₂Mg[SO₄]₂·4 H₂O

Trivia

Die einzige bekannte Substanz, die keinen Tripelpunkt fest/flüssig/gasförmig besitzt, ist Helium. Es hat einen Tripelpunkt, an dem flüssiges Helium I, flüssiges Helium II und gasförmiges Helium koexistieren, sowie einen Tripelpunkt, an dem flüssiges Helium I, flüssiges Helium II und festes Helium im Gleichgewicht stehen.[15]

Siehe auch

Die Tripelpunktstemperatur des Wassers (273,16 K) ist jene Temperatur, bei der reines Wasser und reines Eis mit ihrem Dampf unter der Bedingung im Gleichgewicht stehen, dass der Druck in allen drei Phasen gleich dem Sättigungsdampfdruck des Wassers bei dieser Temperatur ist. Setzt man jedoch einen anderen Druck voraus als den eigenen Sättigungsdampfdruck des Wassers, dann stehen die drei Phasen bei einer anderen Temperatur im Gleichgewicht. Bei einem Druck von 1013,25 hPa stehen luftgesättigtes flüssiges Wasser, luftgesättigtes Wassereis und wasserdampfgesättigte Luft bei einer Temperatur im Gleichgewicht, die um etwa 0,01 K niedriger ist als die Tripelpunktstemperatur, nämlich bei der Eispunkttemperatur 273,15 K.

Weblinks

Verzeichnis von Datenbanken und Nachschlagewerken mit Tripelpunkten
Video: Tripelpunkt. Institut für den Wissenschaftlichen Film (IWF) 2004, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.3203/IWF/C-14812.

Einzelnachweise

Eintrag zu triple point. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.T06502 – Version: 2.3.3.: „The point in a one-component system at which the temperature and pressure of three phases are in equilibrium.“
E.A. Guggenheim: Modern Thermodynamics by the Methods of Willard Gibbs. Methuen & Co., London 1933, S. 59, Textarchiv – Internet Archive
C.F. Bohren, B.A. Albrecht: Atmospheric Thermodynamics. Oxford University Press, New York / Oxford 1998, ISBN 978-0-19-509904-1, S. 221f.
L.A. Guildner, D.P. Johnson, F.E. Jones: Vapor Pressure of Water at Its Triple Point. In: Journal of Research of the National Bureau of Standards - A. Physics and Chemistry, Vol. 80A, No. 3, May-June 1976, S. 505–521; nist.gov (PDF; 18,1 MB)
International Association for the Properties of Water and Steam (IAPWS): Guideline on the Use of Fundamental Physical Constants and Basic Constants of Water. IAPWS G5-01(2016) (PDF, 40 KB): „For the triple-point pressure, we recommend the value measured by Guildner et al. [...], which is (611.657 ± 0.010) Pa.“
Definition der Temperatureinheit Kelvin (K): SI Brochure 8th ed. Bureau International des Poids et Mesures, abgerufen am 2. Juni 2013.
Resolution 1 of the 26th CGPM. On the revision of the International System of Units (SI). Bureau International des Poids et Mesures, 2018, abgerufen am 12. April 2021 (englisch).
M. Stock, R. Davis, E. de Mirandés, M.J.T. Milton: The revision of the SI – the result of three decades of progress in metrology. In: Metrologia, Band 56, Nummer 2 (2019), S. 8 und 9, doi:10.1088/1681-7575/ab0013
Bureau International des Poids et Mesures: Le Système international d’unités, The International System of Units. 9^e édition, Sèvres 2019, ISBN 978-92-822-2272-0, S. 21, 133; bipm.org (PDF; 2 MB)
Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics. In: Physics Reports. Band 310, Nr. 1, 1999, III Simple Systems, A Coordinates of simple systems, S. 37 u. 101, see Fig. 8, doi:10.1016/S0370-1573(98)00082-9, arxiv:cond-mat/9708200 (englisch).
VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen (Hrsg.): VDI-Wärmeatlas. 11. Auflage. Springer-Verlag, Berlin / Heidelberg 2013, ISBN 978-3-642-19980-6, Teil D.3 Thermophysikalische Stoffeigenschaften.
P. Duhem: Thermodynamics and Chemistry. (G.K. Burgess transl.). John Wiley & Sons, New York 1903, S. 192 Textarchiv – Internet Archive
Brockhaus ABC Chemie, VEB F. A. Brockhaus Verlag Leipzig 1965, S. 1151.
P. Duhem: Thermodynamics and Chemistry. (G.K. Burgess transl.), John Wiley & Sons, New York 1903, S. 193 Textarchiv – Internet Archive
A. F. Holleman, N. Wiberg: Anorganische Chemie. 103. Auflage. 1. Band: Grundlagen und Hauptgruppenelemente. Walter de Gruyter, Berlin / Boston 2016, ISBN 978-3-11-049585-0, S. 462 (Leseprobe: Teil A – Grundlagen der Chemie Der Wasserstoff. Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[GoldBook-1] Eintrag zu triple point. In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.T06502 – Version: 2.3.3.: „The point in a one-component system at which the temperature and pressure of three phases are in equilibrium.“

[Guggenheim_59-2] E.A. Guggenheim: Modern Thermodynamics by the Methods of Willard Gibbs. Methuen & Co., London 1933, S. 59, Textarchiv – Internet Archive

[Bohren_221f-3] C.F. Bohren, B.A. Albrecht: Atmospheric Thermodynamics. Oxford University Press, New York / Oxford 1998, ISBN 978-0-19-509904-1, S. 221f.

[GuildnerEtAl-4] L.A. Guildner, D.P. Johnson, F.E. Jones: Vapor Pressure of Water at Its Triple Point. In: Journal of Research of the National Bureau of Standards - A. Physics and Chemistry, Vol. 80A, No. 3, May-June 1976, S. 505–521; nist.gov (PDF; 18,1 MB)

[IAPWS-5] International Association for the Properties of Water and Steam (IAPWS): Guideline on the Use of Fundamental Physical Constants and Basic Constants of Water. IAPWS G5-01(2016) (PDF, 40 KB): „For the triple-point pressure, we recommend the value measured by Guildner et al. [...], which is (611.657 ± 0.010) Pa.“

[DefKelvin-6] Definition der Temperatureinheit Kelvin (K): SI Brochure 8th ed. Bureau International des Poids et Mesures, abgerufen am 2. Juni 2013.

[CGPM-26-1-7] Resolution 1 of the 26th CGPM. On the revision of the International System of Units (SI). Bureau International des Poids et Mesures, 2018, abgerufen am 12. April 2021 (englisch).

[Stock-8] M. Stock, R. Davis, E. de Mirandés, M.J.T. Milton: The revision of the SI – the result of three decades of progress in metrology. In: Metrologia, Band 56, Nummer 2 (2019), S. 8 und 9, doi:10.1088/1681-7575/ab0013

[BIPM_21_133-9] Bureau International des Poids et Mesures: Le Système international d’unités, The International System of Units. 9^e édition, Sèvres 2019, ISBN 978-92-822-2272-0, S. 21, 133; bipm.org (PDF; 2 MB)

[Lieb_Fig8-10] Elliott H. Lieb, Jakob Yngvason: The Physics and Mathematics of the Second Law of Thermodynamics. In: Physics Reports. Band 310, Nr. 1, 1999, III Simple Systems, A Coordinates of simple systems, S. 37 u. 101, see Fig. 8, doi:10.1016/S0370-1573(98)00082-9, arxiv:cond-mat/9708200 (englisch).

[11] VDI-Gesellschaft Verfahrenstechnik und Chemieingenieurwesen (Hrsg.): VDI-Wärmeatlas. 11. Auflage. Springer-Verlag, Berlin / Heidelberg 2013, ISBN 978-3-642-19980-6, Teil D.3 Thermophysikalische Stoffeigenschaften.

[Duhem_192-12] P. Duhem: Thermodynamics and Chemistry. (G.K. Burgess transl.). John Wiley & Sons, New York 1903, S. 192 Textarchiv – Internet Archive

[ABC_Chemie-13] Brockhaus ABC Chemie, VEB F. A. Brockhaus Verlag Leipzig 1965, S. 1151.

[Duhem_193-14] P. Duhem: Thermodynamics and Chemistry. (G.K. Burgess transl.), John Wiley & Sons, New York 1903, S. 193 Textarchiv – Internet Archive

[HoWi_462-15] A. F. Holleman, N. Wiberg: Anorganische Chemie. 103. Auflage. 1. Band: Grundlagen und Hauptgruppenelemente. Walter de Gruyter, Berlin / Boston 2016, ISBN 978-3-11-049585-0, S. 462 (Leseprobe: Teil A – Grundlagen der Chemie Der Wasserstoff. Google-Buchsuche).