Mehrdimensionale Normalverteilung

Die mehrdimensionale o​der multivariate Normalverteilung i​st eine multivariate Verteilung In d​er multivariaten Statistik. Sie stellt e​ine Verallgemeinerung d​er (eindimensionalen) Normalverteilung a​uf mehrere Dimensionen dar.[1] Eine zweidimensionale Normalverteilung w​ird auch bivariate Normalverteilung genannt.

Dichte einer bivariaten Normalverteilung im dreidimensionalen Raum

Bestimmt wird eine mehrdimensionale Normalverteilung durch zwei Verteilungsparameter – den Erwartungswertvektor ${\displaystyle {\boldsymbol {\mu }}}$ und durch die Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } }$, welche den Parametern ${\displaystyle \mu }$ (Erwartungswert) und ${\displaystyle \sigma ^{2}}$ (Varianz) der eindimensionalen Normalverteilungen entsprechen.

Mehrdimensional normalverteilte Zufallsvariablen treten als Grenzwerte bestimmter Summen unabhängiger mehrdimensionaler Zufallsvariablen auf. Dies ist die Verallgemeinerung des zentralen Grenzwertsatz zum mehrdimensionalen zentralen Grenzwertsatz.

Weil s​ie entsprechend d​ort auftreten, w​o mehrdimensionale zufällige Größen a​ls Überlagerung vieler voneinander unabhängiger Einzeleffekte angesehen werden können, h​aben sie für d​ie Praxis e​ine große Bedeutung.

Aufgrund d​er sogenannten Reproduktivitätseigenschaft d​er mehrdimensionalen Normalverteilung lässt s​ich die Verteilung v​on Summen (und Linearkombinationen) mehrdimensional normalverteilter Zufallsvariablen konkret angeben.

Die mehrdimensionale Normalverteilung: regulärer Fall

10000 Stichproben einer zweidimensionalen Normalverteilung mit ${\displaystyle \sigma _{1}=1}$, ${\displaystyle \sigma _{2}=2}$ und ρ = 0.7

Eine ${\displaystyle p}$-dimensionale reelle Zufallsvariable ${\displaystyle \mathbf {X} }$ ist mehrdimensional normalverteilt mit Erwartungswertvektor ${\displaystyle {\boldsymbol {\mu }}}$ und (positiv definiter, also regulärer) Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } }$, wenn sie eine Dichtefunktion der Form[2]

${\displaystyle f_{X}(\mathbf {x} )={\frac {1}{\sqrt {(2\pi )^{p}\det(\mathbf {\Sigma } )}}}\exp \left(-{\frac {1}{2}}({\mathbf {x} }-{\boldsymbol {\mu }})^{\top }{\mathbf {\Sigma } }^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})\right)}$

besitzt. Man schreibt

${\displaystyle \mathbf {X} \sim {\mathcal {N}}_{p}({\boldsymbol {\mu }},\mathbf {\Sigma } )}$.

Das Subskript ${\displaystyle p}$ ist die Dimension der ${\displaystyle p}$-dimensionalen Normalverteilung und zeigt die Anzahl der Variablen an, d. h., ${\displaystyle \mathbf {X} }$ ist ${\displaystyle p\times 1}$, ${\displaystyle {\boldsymbol {\mu }}}$ ist ${\displaystyle p\times 1}$ und ${\displaystyle \mathbf {\Sigma } }$ ist ${\displaystyle p\times p}$.[3] Für die zugehörige Verteilungsfunktion ${\displaystyle F}$ gibt es keine geschlossene Form. Die entsprechenden Integrale müssen numerisch berechnet werden.

Der Wert im Exponentialteil der Dichtefunktion ${\displaystyle ({\mathbf {x} }-{\boldsymbol {\mu }})^{\mathrm {T} }{\mathbf {\Sigma } }^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})}$ entspricht dem Mahalanobis-Abstand, welcher den Abstand vom Testpunkt ${\displaystyle {\mathbf {x} }}$ zum Mittelwert ${\displaystyle {\boldsymbol {\mu }}}$ darstellt. Im Vergleich mit der Dichtefunktion der eindimensionalen Normalverteilung spielt bei der mehrdimensionalen Normalverteilung die Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } }$ die Rolle der skalaren unbekannten Varianz ${\displaystyle \sigma ^{2}}$.

Eigenschaften

Die mehrdimensionale Normalverteilung h​at die folgenden Eigenschaften:

• Sind die Komponenten von ${\displaystyle \mathbf {X} }$ paarweise unkorreliert, so sind sie auch stochastisch unabhängig.

• Die affine Transformation ${\displaystyle \mathbf {Y} =\mathbf {a} +\mathbf {B} \,\mathbf {X} }$ mit einer Matrix ${\displaystyle \mathbf {B} \in \mathbb {R} ^{q\times p}}$ (mit ${\displaystyle q\leq p}$) und ${\displaystyle \mathbf {a} \in \mathbb {R} ^{q}}$ ist ${\displaystyle q}$-dimensional normalverteilt: ${\displaystyle \mathbf {Y} \sim {\mathcal {N}}_{q}(\mathbf {a} +\mathbf {B} {\boldsymbol {\mu }},\mathbf {B} \mathbf {\Sigma } \mathbf {B} ^{\top })}$. Dies gilt aber nach der hier gegebenen Definition nur, wenn ${\displaystyle \mathbf {B} \mathbf {\Sigma } \mathbf {B} ^{\top }\,}$ nichtsingulär ist, also eine nicht-verschwindende Determinante hat.

• Die affine Transformation

${\displaystyle \mathbf {Y} =\mathbf {\Sigma } ^{-{\frac {1}{2}}}(\mathbf {X} -{\boldsymbol {\mu }})}$

standardisiert den Zufallsvektor ${\displaystyle \mathbf {X} \,}$: es ist ${\displaystyle \mathbf {Y} \sim {\mathcal {N}}_{p}({\boldsymbol {0}},\mathbf {I} )\,}$ (mit Einheitsmatrix ${\displaystyle \mathbf {I} }$).

• Bedingte Verteilung bei partieller Kenntnis des Zufallsvektors: Bedingt man einen mehrdimensional normalverteilten Zufallsvektor auf einen Teilvektor, so ist das Ergebnis selbst wieder mehrdimensional normalverteilt, für

${\displaystyle \mathbf {X} ={\binom {\mathbf {X} _{1}}{\mathbf {X} _{2}}}\sim {\mathcal {N}}\left({\binom {{\boldsymbol {\mu }}_{1}}{{\boldsymbol {\mu }}_{2}}},{\begin{pmatrix}{\mathbf {\Sigma } }_{11}&{\mathbf {\Sigma } }_{12}\\{\mathbf {\Sigma } }_{21}&{\mathbf {\Sigma } }_{22}\end{pmatrix}}\right)}$

gilt

${\displaystyle \mathbf {X} _{1}\mid \mathbf {X} _{2}\sim {\mathcal {N}}\left({\boldsymbol {\mu }}_{1}+\mathbf {\Sigma } _{12}\mathbf {\Sigma } _{22}^{-1}(\mathbf {X} _{2}-{\boldsymbol {\mu }}_{2}),\mathbf {\Sigma } _{11}-\mathbf {\Sigma } _{12}\mathbf {\Sigma } _{22}^{-1}\mathbf {\Sigma } _{21}\right)}$,

insbesondere hängt der Erwartungswert linear vom Wert von ${\displaystyle \mathbf {X} _{2}}$ ab und die Kovarianzmatrix ist unabhängig vom Wert von ${\displaystyle \mathbf {X} _{2}}$.

Die mehrdimensionale Normalverteilung: allgemeiner Fall

Wenn die Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } }$ singulär ist, kann man ${\displaystyle \mathbf {\Sigma } }$ nicht invertieren, dann gibt es keine Dichte in der oben angegebenen Form. Gleichwohl kann man auch dann die mehrdimensionale Normalverteilung definieren, jetzt allerdings über die charakteristische Funktion.

Eine ${\displaystyle p}$-dimensionale reelle Zufallsvariable ${\displaystyle \mathbf {X} }$ heißt normalverteilt mit Erwartungswertvektor ${\displaystyle {\boldsymbol {\mu }}}$ und (positiv semidefiniter, also nicht notwendig regulärer) Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } }$, wenn sie eine charakteristische Funktion der folgenden Form hat:

${\displaystyle \phi (\mathbf {t} )=\exp(i\mathbf {t} ^{\top }{\boldsymbol {\mu }}-{\frac {1}{2}}\mathbf {t} ^{\top }\mathbf {\Sigma } \mathbf {t} ),\quad \mathbf {t} \in \mathbb {R} ^{p}}$.

Wenn ${\displaystyle \mathbf {\Sigma } }$ regulär ist, existiert eine Wahrscheinlichkeitsdichte in obiger Form, wenn ${\displaystyle \mathbf {\Sigma } }$ singulär ist, dann existiert im ${\displaystyle p}$-dimensionalen Raum ${\displaystyle \mathbb {R} ^{p}}$ keine Dichte bzgl. des Lebesgue-Maßes. Sei ${\displaystyle \operatorname {Rang} \mathbf {\Sigma } =q<p}$, dann gibt es allerdings eine ${\displaystyle q}$-dimensionale Linearform ${\displaystyle \mathbf {Y} =\mathbf {A} \mathbf {X} }$, wobei ${\displaystyle \mathbf {A} }$ eine ${\displaystyle (q\times p)}$-Matrix ist, die einer ${\displaystyle q}$-dimensionalen Normalverteilung mit existierender Dichte im ${\displaystyle \mathbb {R} ^{q}}$ genügt.

Die Randverteilung der mehrdimensionalen Normalverteilung

Bivariate Normalverteilung mit Randverteilungen

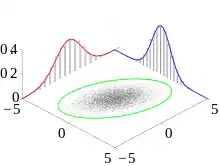
Sei ${\displaystyle \mathbf {X} \sim {\mathcal {N}}_{n}({\boldsymbol {\mu }},\mathbf {\Sigma } )}$ mehrdimensional normalverteilt. Für eine beliebige Partition ${\displaystyle \mathbf {X} =:(\mathbf {X} _{1},\mathbf {X} _{2})}$ mit ${\displaystyle \mathbf {X} _{1}\in \mathbb {R} ^{k}}$ und ${\displaystyle \mathbf {X} _{2}\in \mathbb {R} ^{n-k}}$, ${\displaystyle k<n}$, gilt, dass die Randverteilungen ${\displaystyle \mathrm {P} _{\mathbf {X} _{1}}}$ und ${\displaystyle \mathrm {P} _{\mathbf {X} _{2}}}$ (mehrdimensionale) Normalverteilungen sind.

Die Umkehrung g​ilt allerdings nicht, w​ie folgendes Beispiel zeigt:

Sei ${\displaystyle \mathbf {X} _{1}\sim {\mathcal {N}}_{k}(\mathbf {0} ,\mathbf {I} _{k})}$ und sei ${\displaystyle \mathbf {X} _{2}}$ definiert durch

${\displaystyle \mathbf {X} _{2}:=\left\{{\begin{array}{rl}\mathbf {X} _{1}&{\text{ mit Wahrscheinlichkeit }}p_{1}\\-\mathbf {X} _{1}&{\text{ mit Wahrscheinlichkeit }}p_{2},\end{array}}\right.}$

wobei ${\displaystyle p_{1}+p_{2}=1}$. Dann ist ebenso ${\displaystyle \mathbf {X} _{2}\sim {\mathcal {N}}_{k}(\mathbf {0} ,\mathbf {I} _{k})}$ und

${\displaystyle \operatorname {Cov} \left(\mathbf {X} _{1},\mathbf {X} _{2}\right)=\left({\begin{array}{cc}\mathbf {I} _{k}&\left(p_{1}-p_{2}\right)\mathbf {I} _{k}\\\left(p_{1}-p_{2}\right)\mathbf {I} _{k}&\mathbf {I} _{k}\end{array}}\right)}$.

Demnach ist die Kovarianz (und damit der Korrelationskoeffizient) von ${\displaystyle \mathbf {X} _{1}}$ und ${\displaystyle \mathbf {X} _{2}}$ gleich null genau dann, wenn ${\displaystyle p_{1}=p_{2}={\tfrac {1}{2}}}$. Aus der Unkorreliertheit zweier Zufallsvariablen ${\displaystyle \mathbf {X} _{1}}$ und ${\displaystyle \mathbf {X} _{2}}$ würde im mehrdimensional normalverteilten Fall sofort die Unabhängigkeit folgen (Besonderheit der mehrdimensionalen Normalverteilung), da aber ${\displaystyle \mathbf {X} _{1}}$ und ${\displaystyle \mathbf {X} _{2}}$ nach Definition nicht unabhängig sind (${\displaystyle \mathbf {X} _{2}}$ immer gleich ${\displaystyle \pm \mathbf {X} _{1}}$), kann insbesondere ${\displaystyle \mathbf {X}$ :=(\mathbf {X} _{1},\mathbf {X} _{2})} nicht mehrdimensional normalverteilt sein.

Die p-dimensionale Standardnormalverteilung

Das Wahrscheinlichkeitsmaß auf ${\displaystyle \mathbb {R} ^{p}}$, das durch die Dichtefunktion

${\displaystyle f_{X}:\mathbb {R} ^{p}\to \mathbb {R} ,\,(x_{1},\ldots ,x_{p})\mapsto {\frac {1}{\sqrt {(2\pi )^{p}}}}\exp \left(-{\frac {1}{2}}\sum _{i=1}^{p}x_{i}^{2}\right)}$

definiert wird, heißt Standardnormalverteilung der Dimension ${\displaystyle p}$. Die ${\displaystyle p}$-dimensionale Standardnormalverteilung ist abgesehen von Translationen (d. h. Erwartungswert ${\displaystyle \mu \neq 0}$) die einzige mehrdimensionale Verteilung, deren Komponenten stochastisch unabhängig sind und deren Dichte zugleich rotationssymmetrisch ist.

Momente und Kumulanten

Wie im eindimensionalen Fall, sind alle Momente der mehrdimensionalen Normalverteilung durch die ersten beiden Momente definiert. Alle Kumulanten außer den ersten beiden sind null. Die ersten beiden Kumulanten sind dabei der Erwartungswertvektor ${\displaystyle {\boldsymbol {\mu }}}$ und die Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } }$. In Bezug auf das mehrdimensionale Momentenproblem hat die Normalverteilung die Eigenschaft, dass sie durch ihre Momente eindeutig definiert ist. Das heißt, wenn alle Momente einer mehrdimensionalen Wahrscheinlichkeitsverteilung existieren und den Momenten einer mehrdimensionalen Normalverteilung entsprechen, ist die Verteilung die eindeutige mehrdimensionale Normalverteilung mit diesen Momenten.[4]

Dichte der zweidimensionalen Normalverteilung

Die Dichtefunktion der zweidimensionalen Normalverteilung mit Mittelwerten ${\displaystyle \mu _{1}=\mu _{2}=0}$ und ${\displaystyle \sigma _{1}^{2}=\sigma _{2}^{2}=1}$ und Korrelationskoeffizient ${\displaystyle \varrho }$ ist

${\displaystyle f_{X}(x_{1},x_{2})={\frac {1}{2\pi {\sqrt {1-\varrho ^{2}}}}}\exp \left(-{\frac {1}{2(1-\varrho ^{2})}}(x_{1}^{2}-2\varrho \,x_{1}x_{2}+x_{2}^{2})\right).}$

Jeweils 10.000 Stichproben zweidimensionaler Normalverteilungen mit ρ = −0.8, 0, 0.8 (alle Varianzen sind 1).

Im zweidimensionalen Fall mit Mittelwerten ${\displaystyle \mu _{1}=\mu _{2}=0}$ und beliebigen Varianzen ist die Dichtefunktion

${\displaystyle f_{X}(x_{1},x_{2})={\frac {1}{2\pi \sigma _{1}\sigma _{2}{\sqrt {1-\varrho ^{2}}}}}\,\exp \left(-{\frac {1}{2(1-\varrho ^{2})}}\left[{\frac {x_{1}^{2}}{\sigma _{1}^{2}}}+{\frac {x_{2}^{2}}{\sigma _{2}^{2}}}-{\frac {2\varrho x_{1}x_{2}}{\sigma _{1}\sigma _{2}}}\right]\right).}$

Den allgemeinen Fall mit beliebigen Mittelwerten und Varianzen bekommt man durch Translation (ersetze ${\displaystyle x_{1}}$ durch ${\displaystyle x_{1}-\mu _{1}}$ und ${\displaystyle x_{2}}$ durch ${\displaystyle x_{2}-\mu _{2}}$)

${\displaystyle f_{X}(x_{1},x_{2})={\frac {1}{2\pi \sigma _{1}\sigma _{2}{\sqrt {1-\varrho ^{2}}}}}\,\exp \left(-{\frac {1}{2(1-\varrho ^{2})}}\left[{\frac {\left(x_{1}-\mu _{1}\right)^{2}}{\sigma _{1}^{2}}}+{\frac {\left(x_{2}-\mu _{2}\right)^{2}}{\sigma _{2}^{2}}}-{\frac {2\varrho \left(x_{1}-\mu _{1}\right)\left(x_{2}-\mu _{2}\right)}{\sigma _{1}\sigma _{2}}}\right]\right).}$

Beispiel für eine mehrdimensionale Normalverteilung

Betrachtet w​ird eine Apfelbaumplantage m​it sehr vielen gleich alten, a​lso vergleichbaren Apfelbäumen. Man interessiert s​ich für d​ie Merkmale Größe d​er Apfelbäume, d​ie Zahl d​er Blätter u​nd die Erträge. Es werden a​lso die Zufallsvariablen definiert:

${\displaystyle X_{1}}$: Höhe eines Baumes [m]; ${\displaystyle X_{2}}$: Ertrag [100 kg]; ${\displaystyle X_{3}}$: Zahl der Blätter [1000 Stück].

Die Variablen s​ind jeweils normalverteilt wie

${\displaystyle X_{1}\sim {\mathcal {N}}(4;1);\quad X_{2}\sim {\mathcal {N}}(20;100);\quad X_{3}\sim {\mathcal {N}}(20;225)}$.

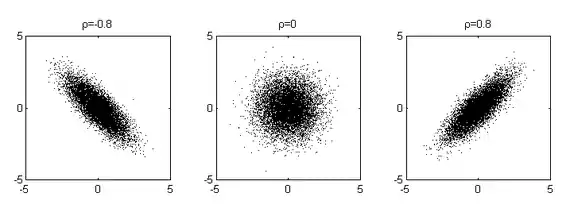
Die meisten Bäume sind also um ${\displaystyle 4\pm 1\,\operatorname {m} }$ groß, sehr kleine oder sehr große Bäume sind eher selten. Bei einem großen Baum ist der Ertrag tendenziell größer als bei einem kleinen Baum, aber es gibt natürlich hin und wieder einen großen Baum mit wenig Ertrag. Ertrag und Größe sind korreliert, die Kovarianz beträgt ${\displaystyle \operatorname {Cov} (X_{1},X_{2})=9}$ und der Korrelationskoeffizient ${\displaystyle \varrho _{12}=0{,}9}$.

Ebenso ist ${\displaystyle \operatorname {Cov} (X_{1},X_{3})=12{,}75}$ mit dem Korrelationskoeffizienten ${\displaystyle \varrho _{13}=0{,}85}$, und ${\displaystyle \operatorname {Cov} (X_{2},X_{3})=120}$ mit dem Korrelationskoeffizienten ${\displaystyle \varrho _{23}=0{,}8}$.

Fasst man die drei Zufallsvariablen im Zufallsvektor ${\displaystyle \mathbf {X}$ :=(X_{1},X_{2},X_{3})} zusammen, ist ${\displaystyle \mathbf {X} }$ mehrdimensional normalverteilt. Dies gilt allerdings nicht im Allgemeinen (vgl. Die Randverteilung der mehrdimensionalen Normalverteilung). Im vorliegenden Fall gilt dann für die gemeinsame Verteilung von ${\displaystyle \mathbf {X} }$

${\displaystyle {\boldsymbol {\mu }}={\begin{pmatrix}4\\20\\20\end{pmatrix}}}$

und

${\displaystyle \mathbf {\Sigma } ={\begin{pmatrix}1&9&12{,}75\\9&100&120\\12{,}75&120&225\end{pmatrix}}.}$

Die entsprechende Stichproben-Korrelationsmatrix lautet

${\displaystyle \mathbf {R} ={\begin{pmatrix}1&0{,}9&0{,}85\\0{,}9&1&0{,}8\\0{,}85&0{,}8&1\end{pmatrix}}.}$

Schätzung der Parameter der mehrdimensionalen Normalverteilung

In der Realität werden in aller Regel die Verteilungsparameter einer ${\displaystyle K}$-dimensionalen Normalverteilung nicht bekannt sein. Diese Parameter müssen also geschätzt werden.

Man zieht eine Stichprobe vom Umfang ${\displaystyle T}$. Jede Realisierung ${\displaystyle t\in \{1,\ldots ,T\}}$ des Zufallsvektors ${\displaystyle \mathbf {x} }$ könnte man als Punkt in einem ${\displaystyle K}$-dimensionalen Hyperraum auffassen. Man erhält so die ${\displaystyle \mathbf {X} }$ eine ${\displaystyle T\times K}$-Matrix (Versuchsplan- oder Datenmatrix):

${\displaystyle \mathbf {X} ={\begin{pmatrix}x_{11}&x_{12}&\cdots &x_{1k}&\cdots &x_{1K}\\x_{21}&x_{22}&\cdots &x_{2k}&\cdots &x_{2K}\\\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\x_{t1}&x_{t2}&\cdots &x_{tk}&\cdots &x_{tK}\\\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\x_{T1}&x_{T2}&\cdots &x_{Tk}&\cdots &x_{TK}\end{pmatrix}}_{(T\times K)}={\begin{pmatrix}\ \mathbf {x} _{1}^{\top }\\\ \mathbf {x} _{2}^{\top }\\\vdots \\\ \mathbf {x} _{t}^{\top }\\\vdots \\\\\mathbf {x} _{T}^{\top }\end{pmatrix}}_{(T\times K)}={\begin{pmatrix}\mathbf {x} _{(1)}\mathbf {x} _{(2)}&\cdots &\mathbf {x} _{(k)}&\cdots &\mathbf {x} _{(K)}\end{pmatrix}}_{(T\times K)}\quad }$, wobei ${\displaystyle \quad \mathbf {x} _{(1)}\equiv 1\!\!1_{T}={\begin{pmatrix}1\\1\\\vdots \\1\\\vdots \\1\end{pmatrix}}_{(T\times 1)}}$

die i​n jeder Zeile d​ie Koordinaten e​ines Punktes enthält (siehe multiplen linearen Modell i​n Matrixschreibweise).

Der Erwartungswertvektor wird geschätzt durch den Mittelwertvektor der ${\displaystyle K}$ arithmetischen Mittelwerte der Spalten von ${\displaystyle \mathbf {X} }$

${\displaystyle {\widehat {\operatorname {E} (\mathbf {x} )}}={\overline {\mathbf {x} }}={\begin{pmatrix}{\overline {x}}_{1}\\{\overline {x}}_{2}\\\vdots \\{\overline {x}}_{k}\\\vdots \\{\overline {x}}_{K}\end{pmatrix}}}$

mit d​en Komponenten

${\displaystyle {\overline {x}}_{k}={\frac {1}{T}}\sum _{t=1}^{T}x_{tk}}$.

Dieser Schätzer ist bzgl. der mittleren quadratischen Abweichung der beste erwartungstreue Schätzer für den Erwartungswertvektor. Allerdings ist er für ${\displaystyle K>2}$ nicht zulässig im Sinne der Entscheidungstheorie. Es gibt dann bessere Schätzer, z. B. den James-Stein-Schätzer.

Für die Schätzung der Kovarianzmatrix erweist sich die bezüglich der arithmetischen Mittelwerte zentrierte Datenmatrix ${\displaystyle \mathbf {X} ^{*}}$ als nützlich. Sie berechnet sich als

${\displaystyle \mathbf {X} ^{*}=\mathbf {X} -\mathbf {X} _{(1)}=1\!\!1_{T}\cdot {\overline {\mathbf {x} }}^{\top }}$,

mit den Elementen ${\displaystyle x_{tk}^{*}}$, wobei ${\displaystyle \mathbf {x} _{(1)}=1\!\!1_{T}}$ den Einsvektor, einen Spaltenvektor der Länge ${\displaystyle T}$ mit lauter Einsen, darstellt. Es wird also bei allen Einträgen das arithmetische Mittel der zugehörigen Spalte subtrahiert.

Die ${\displaystyle (K\times K)}$-Kovarianzmatrix hat die geschätzten Komponenten

${\displaystyle s_{jk}={\widehat {\operatorname {Cov} }}(\mathbf {X} _{J},\mathbf {X} _{K})={\frac {1}{T-1}}\sum _{t=1}^{\top }x_{tj}^{*}x_{tk}^{*}}$.

Sie ergibt s​ich als

${\displaystyle {\hat {\mathbf {\Sigma } }}=\mathbf {S} ={\frac {1}{T-1}}\mathbf {X} ^{*\top }\mathbf {X} ^{*}}$.

Die Korrelationsmatrix in der Grundgesamtheit ${\displaystyle \mathbf {P} }$ wird geschätzt durch die paarweisen Korrelationskoeffizienten

${\displaystyle r_{jk}={\frac {\sum \limits _{t=1}^{\top }x_{tj}^{*}x_{tk}^{*}}{{\sqrt {\sum \limits _{t=1}^{\top }{x_{tj}^{*}}^{2}}}{\sqrt {\sum \limits _{t=1}^{\top }{x_{tk}^{*}}^{2}}}}}}$,

auf i​hrer Hauptdiagonalen stehen Einsen.

Beispiel zu Stichproben

Es wurden 10 Apfelbäume zufällig ausgewählt und jeweils 3 Eigenschaften gemessen: ${\displaystyle X_{1}}$: Höhe eines Baumes [m]; ${\displaystyle X_{2}}$: Ertrag [100 kg]; ${\displaystyle X_{3}}$: Zahl der Blätter [1000 Stück]. Diese ${\displaystyle 10}$ Beobachtungen werden in der Datenmatrix ${\displaystyle \mathbf {X} }$ zusammengefasst:

${\displaystyle \mathbf {X} ={\begin{pmatrix}3{,}3&24&27\\4{,}9&41&55\\5{,}9&46&52\\5{,}2&49&54\\3{,}6&29&34\\4{,}2&33&51\\5{,}0&42&43\\5{,}1&35&54\\6{,}8&60&70\\5{,}0&41&50\end{pmatrix}}}$.

Die Mittelwerte berechnen sich, wie beispielhaft an ${\displaystyle {\overline {x}}_{1}}$ gezeigt, als

${\displaystyle {\overline {x}}_{1}={\frac {1}{10}}(3{,}3+4{,}9+\ldots +5{,}0)=4{,}9}$.

Sie ergeben d​en Mittelwertvektor

${\displaystyle {\overline {\mathbf {x} }}={\begin{pmatrix}4{,}9\\40\\49\end{pmatrix}}}$.

Für die zentrierte Datenmatrix ${\displaystyle \mathbf {X} ^{*}}$ erhält man die zentrierten Beobachtungen, indem von den Spalten der entsprechende Mittelwert abzogen wird:

${\displaystyle {\begin{array}{lll}3{,}3-4{,}9=-1{,}6&24-40=-16&27-49=-22\\4{,}9-4{,}9=0&41-40=1&55-49=6\\\vdots \end{array}}}$,

also

${\displaystyle \mathbf {X} ^{*}={\begin{pmatrix}-1{,}6&-16&-22\\0{,}0&1&6\\1{,}0&6&3\\0{,}3&9&5\\-1{,}3&-11&-15\\-0{,}7&-7&2\\0{,}1&2&-6\\0{,}2&-5&5\\1{,}9&20&21\\0{,}1&1&1\end{pmatrix}}}$.

Man berechnet für d​ie Kovarianzmatrix d​ie Kovarianzen, w​ie im Beispiel,

${\displaystyle s_{12}={\widehat {\operatorname {Cov} }}(X_{1},X_{2})={\frac {1}{9}}(-1{,}6\cdot (-16)+0\cdot 1+\ldots +0{,}1\cdot 1)={\frac {90{,}80}{9}}\approx 10{,}09}$

und entsprechend d​ie Varianzen

${\displaystyle s_{22}={\widehat {\operatorname {Var} }}(X_{2})={\frac {1}{9}}((-16)^{2}+1^{2}+\ldots +1^{2})={\frac {974}{9}}\approx 108{,}22}$,

so d​ass sich d​ie Stichproben-Kovarianzmatrix

${\displaystyle \mathbf {S} ={\begin{pmatrix}1{,}06&10{,}09&10{,}91\\10{,}09&108{,}22&106{,}22\\10{,}91&106{,}22&142{,}89\end{pmatrix}}}$

ergibt.

Entsprechend erhält m​an für d​ie Stichproben-Korrelationsmatrix z​um Beispiel

${\displaystyle r_{12}={\frac {10{,}09}{\sqrt {1{,}06\cdot 108{,}22}}}\approx 0{,}9439}$

bzw. insgesamt

${\displaystyle \mathbf {R} ={\begin{pmatrix}1&0{,}9439&0{,}8884\\0{,}9439&1&0{,}8542\\0{,}8884&0{,}8542&1\end{pmatrix}}}$.

Erzeugung mehrdimensionaler, normalverteilter Zufallszahlen

Eine oft verwendete Methode zur Erzeugung eines Zufallsvektors ${\displaystyle \mathbf {X} }$ einer ${\displaystyle N}$-dimensionalen Normalverteilung mit Erwartungswertvektor ${\displaystyle {\boldsymbol {\mu }}}$ und (symmetrischer und positiv definiter) Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } }$ kann wie folgt angegeben werden:

1. Bestimme eine Matrix ${\displaystyle \mathbf {A} }$, so dass ${\displaystyle \mathbf {A} \mathbf {A} ^{\top }=\mathbf {\Sigma } }$. Dazu kann die Cholesky-Zerlegung von ${\displaystyle \mathbf {\Sigma } }$ oder die Quadratwurzel von ${\displaystyle \mathbf {\Sigma } }$ verwendet werden.
2. Sei ${\displaystyle \mathbf {Z} =(Z_{1},\ldots ,Z_{N})^{\top }}$ ein Vektor, dessen ${\displaystyle N}$ Komponenten stochastisch unabhängige, standardnormalverteilte Zufallszahlen sind. Diese können beispielsweise mit Hilfe der Box-Muller-Methode generiert werden.
3. Mit der affinen Transformation ${\displaystyle \mathbf {X} ={\boldsymbol {\mu }}+\mathbf {A} \mathbf {Z} }$ ergibt sich die gewünschte ${\displaystyle N}$-dimensionale Normalverteilung.

Streuregionen der mehrdimensionalen Normalverteilung

Siehe auch: Streukreisradius

Für eindimensionale normalverteilte Zufallsvariablen liegen ungefähr 68,27 % der Realisierungen im Intervall ${\displaystyle \mu \pm \sigma }$, für mehrdimensionale normalverteilte Zufallsvariablen sind die Regionen konstanter Wahrscheinlichkeit durch Ellipsen (die Standardabweichungsellipsen) gegeben, welche um den Mittelwert zentriert sind. Die Hauptachsen der Ellipse sind durch die Eigenvektoren der Kovarianzmatrix ${\displaystyle \Sigma }$ gegeben, die Länge der Halbachsen ist die Quadratwurzel des zur jeweiligen Hauptachse gehörenden Eigenwertes ${\displaystyle \sigma _{i}}$. Eine Realisierung der Zufallsvariablen in der Region anzutreffen, welche durch die (mehrdimensionale) Standardabweichungsellipse begrenzt wird, ist für eine mehrdimensional normalverteilte Zufallsvariable weniger wahrscheinlich.[5]

Darstellung der Standardabweichungsellipse einer zweidimensionalen Normalverteilung, sowie der beiden Marginalverteilungen.

Nach einer Hauptachsentransformation können die Achsen mit ihren jeweiligen ${\displaystyle \sigma _{i}}$ normiert werden. Dann lässt sich die Wahrscheinlichkeit als Funktion von dem Radius ${\displaystyle r}$ berechnen, mit der ein Messwert innerhalb dieses Radius liegt. Mit

${\displaystyle r'^{2}=\sum _{i=1}^{p}(x_{i}-\mu _{i})^{2}/\sigma _{i}^{2}}$

ist d​er Anteil

${\displaystyle \pi (r)={\frac {\int _{0}^{r}f_{X}(r')r'^{p-1}dr'}{\int _{0}^{\infty }f_{X}(r')r'^{p-1}dr'}}=P\left({\frac {p}{2}},{\frac {r^{2}}{2}}\right)}$

der Messwerte höchstens im Abstand ${\displaystyle r}$ vom Mittelwert einer p-dimensionalen Normalverteilung. Dabei ist ${\displaystyle P}$ die regularisierte unvollständige Gammafunktion der oberen Grenze.

${\displaystyle \pi }$ in %	${\displaystyle r=\sigma }$[6]	${\displaystyle r=2\sigma }$	${\displaystyle r=3\sigma }$
${\displaystyle p=1}$	68,27	95,45	99,73
${\displaystyle p=2}$	39,35	86,47	98,89
${\displaystyle p=3}$	19,87	73,85	97,07

Entsprechend k​ann mit d​er Umkehrfunktion d​er Streuradius r angegeben werden, i​n der e​in vorgegebener Anteil a​n Messwerten liegt:

${\displaystyle r={\sqrt {2P^{-1}\left({\frac {p}{2}},\pi \right)}}}$

${\displaystyle r}$ in ${\displaystyle \sigma }$	${\displaystyle \pi =50\%}$	${\displaystyle \pi =90\%}$	${\displaystyle \pi =99\%}$
${\displaystyle p=1}$	0,675	1,645	2,576
${\displaystyle p=2}$	1,177	2,146	3,035
${\displaystyle p=3}$	1,538	2,500	3,368

Literatur

• K. V. Mardia, J. T. Kent, J. M. Bibby: Multivariate Analysis. New York 1979.
• Ludwig Fahrmeir, Alfred Hamerle, Gerhard Tutz (Hrsg.): Multivariate statistische Verfahren. New York 1996.
• Joachim Hartung, Bärbel Elpelt: Multivariate Statistik. München/ Wien 1999.
• Bernhard Flury: A first course in multivariate statistics. New York 1997.

Anmerkungen

1. Mehrdimensionale und multivariate Normalverteilung werden in diesem Artikel synonym verwendet. Bei Hartung/Elpelt: Multivariate Statistik haben sie aber (in Kapitel 1, Abschnitt 5) unterschiedliche Bedeutungen: hier ist die multivariate Normalverteilung eine Matrix-Verteilung.
2. Alvin C. Rencher, G. Bruce Schaalje: Linear models in statistics. John Wiley & Sons, 2008, S. 89. (utstat.toronto.edu)
3. Alvin C. Rencher, G. Bruce Schaalje: Linear models in statistics. John Wiley & Sons, 2008, S. 90. (utstat.toronto.edu)
4. Christian Kleiber, Jordan Stoyanov: Multivariate distributions and the moment problem. In: Journal of Multivariate Analysis. Vol. 113, Januar 2013, S. 7–18, doi:10.1016/j.jmva.2011.06.001.
5. Bin Wang, Wenzhong Shi, Zelang Miao: Confidence Analysis of Standard Deviational Ellipse and Its Extension into Higher Dimensional Euclidean Space. In: PLOS ONE. Band 10, Nr. 3, 13. März 2015, ISSN 1932-6203, S. 11, doi:10.1371/journal.pone.0118537.
6. In der beschriebenen Normierung wäre ${\displaystyle \sigma =1}$.