Extremwertverteilung

Die verallgemeinerte Extremwertverteilung[1][2] ist eine stetige Wahrscheinlichkeitsverteilung. Sie spielt eine herausragende Rolle in der Extremwerttheorie, da sie alle möglichen asymptotischen Verteilungen des Maximums einer einfachen Zufallsstichprobe in einer Darstellung zusammenfasst. Die verallgemeinerte Extremwertverteilung fasst die Weibull-Verteilung, die Fréchet-Verteilung und die Gumbel-Verteilung zusammen.

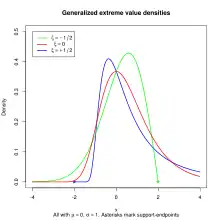
Beispiele der Wahrscheinlichkeitsdichtefunktionen der Extremwertverteilungsfamilie.

Definition

Eine stetige Zufallsgröße ${\displaystyle X}$ genügt einer verallgemeinerten Extremwertverteilung mit den Parametern ${\displaystyle \mu \in \mathbb {R} }$, ${\displaystyle \sigma >0}$ und ${\displaystyle \xi \in \mathbb {R} }$, wenn sie die Wahrscheinlichkeitsdichte

${\displaystyle f(x)={\begin{cases}{\frac {1}{\sigma }}\,t(x)^{\xi +1}e^{-t(x)}&{\text{falls }}1+\xi ({\tfrac {x-\mu }{\sigma }})>0\\0&{\text{sonst}}\end{cases}}}$

mit

${\displaystyle t(x)={\begin{cases}{\big (}1+\xi ({\tfrac {x-\mu }{\sigma }}){\big )}^{-1/\xi }&{\textrm {falls}}\ \xi \neq 0\\e^{-(x-\mu )/\sigma }&{\textrm {falls}}\ \xi =0\end{cases}}}$

besitzt. Für ${\displaystyle \xi =0}$ liegt eine Gumbel-Verteilung, für ${\displaystyle \xi >0}$ eine Fréchet-Verteilung und für ${\displaystyle \xi <0}$ eine Weibull-Verteilung vor.

Einzelnachweise

1. Paul Embrechts, Claudia Klüppelberg, Thomas Mikosch: Modelling Extremal Events for Insurance and Finance. Springer, Berlin 1997, ISBN 3-540-60931-8, S. 152–168.
2. Eric W. Weisstein: Extreme Value Distribution. Abgerufen am 6. August 2021 (englisch).