Benfordsches Gesetz

Das Benfordsche Gesetz, auch Newcomb-Benford’s Law (NBL), beschreibt eine Gesetzmäßigkeit in der Verteilung der führenden Ziffern von ganzen Zahlen in empirischen Datensätzen, wenn die zugrunde liegenden Werte eine ausreichend große Streubreite aufweisen.

Das Gesetz lässt sich etwa in Datensätzen über Einwohnerzahlen von Städten, Geldbeträge in der Buchhaltung, Naturkonstanten etc. beobachten. Kurzgefasst besagt es:

Je niedriger der zahlenmäßige Wert einer Ziffernsequenz bestimmter Länge an einer bestimmten Stelle einer Zahl ist, desto wahrscheinlicher ist ihr Auftreten. Für die Anfangsziffern in Zahlen des Zehnersystems gilt zum Beispiel: Zahlen mit der Anfangsziffer 1 treten etwa 6,6-mal so häufig auf wie Zahlen mit der Anfangsziffer 9.

Entdeckung

1881 wurde diese Gesetzmäßigkeit von dem Astronomen und Mathematiker Simon Newcomb entdeckt und im American Journal of Mathematics publiziert. Er hatte bemerkt, dass in den benutzten Büchern mit Logarithmentafeln die Seiten mit Tabellen mit Eins als erster Ziffer deutlich schmutziger waren als die anderen Seiten, weil sie offenbar öfter benutzt worden waren. Die Abhandlung Newcombs blieb unbeachtet und war schon in Vergessenheit geraten, als der Physiker Frank Benford (1883–1948) dieselbe Gesetzmäßigkeit wiederentdeckte und sie 1938 erneut publizierte. Seither war sie nach ihm benannt, in neuerer Zeit wird aber durch die Bezeichnung „Newcomb-Benford’s Law“ (NBL) der ursprüngliche Entdecker ebenfalls bedacht. Die Existenz einer solchen Gesetzmäßigkeit war selbst unter Statistikern nicht vielen bewusst, bis der US-amerikanische Mathematiker Theodore Hill versuchte, die Benford-Verteilung zur Lösung praktischer Probleme nutzbar zu machen, und sie dadurch wesentlich bekannter machte.

Benfordsche Verteilung

Benfordsches Gesetz

Das Benfordsche Gesetz besagt, dass für empirisch gegebene Zahlen die Ziffer $d$ mit Wahrscheinlichkeit

p(d)=\log _{10}\left(1+{\frac {1}{d}}\right)=\log _{10}\left(d+1\right)-\log _{10}\left(d\right)

als erste (von Null verschiedene) Ziffer in der Dezimaldarstellung der Zahlen vorkommen wird.

Grafische Darstellung

Benfords Gesetz besagt in seiner einfachsten Konsequenz, dass die führenden Ziffern $d$ $(d=1,\ldots ,9)$ mit folgenden Wahrscheinlichkeiten erscheinen: $\log _{10}(d+1)-\log _{10}(d)$ , oder

Grafische Darstellung der Tabelle

Führende Ziffer	Wahrscheinlichkeit
1	30,1 %
2	17,6 %
3	12,5 %
4	9,7 %
5	7,9 %
6	6,7 %
7	5,8 %
8	5,1 %
9	4,6 %

Verallgemeinerung

Gegeben sei eine Menge von Zahlen, die dem Benfordschen Gesetz gehorcht. Dann ist die Wahrscheinlichkeit des Auftretens der Ziffer $d$ zur Basis $B$ an der $n$ -ten Stelle (gezählt von vorne, startend mit 0):

p_{n}(d)=\sum _{k=\lfloor B^{n-1}\rfloor }^{B^{n}-1}\log _{B}\left(1+{\frac {1}{k\cdot B+d}}\right)

wobei $\lfloor \cdot \rfloor$ die Gaußklammer bezeichnet.

Speziell für die erste Ziffer vereinfacht sich die Formel zu

p(d)=p_{0}(d)=\log _{B}\left(1+{\frac {1}{d}}\right)=\log _{B}\left(d+1\right)-\log _{B}\left(d\right)

Leicht nachprüfbar ist, dass die Summe der Wahrscheinlichkeiten aller verschiedenen Ziffern an einer bestimmten Stelle 1 ergibt, da die Summe nach Anwendung des oben schon für die erste Stelle verwendeten Logarithmengesetzes eine Teleskopsumme ergibt.

Gültigkeit des NBL

Ein Datensatz ist eine Benford-Variable (das heißt, das Benfordsche Gesetz gilt für diesen Datensatz), wenn die Mantissen der Logarithmen des Datensatzes in den Grenzen von 0 bis 1 gleichverteilt sind; dies ist im Allgemeinen dann der Fall, wenn die Varianz innerhalb des Datensatzes einen bestimmten, von der Klasse der Verteilung, nach welcher die Logarithmen des Datensatzes verteilt sind, abhängigen Mindestwert nicht unterschreitet.

Bei den Fibonacci-Zahlen (jede Fibonacci-Zahl ist die Summe ihrer beiden Vorgänger) ergeben schon die Anfangsziffern der ersten 30 Zahlen eine Verteilung, die verblüffend nahe an einer Benford-Verteilung liegt. Dies gilt auch für ähnliche Folgen mit geänderten Anfangszahlen (z. B. die Lucas-Folgen). Viele Zahlenfolgen gehorchen dem Benfordschen Gesetz, viele andere gehorchen ihm aber nicht, sind also keine Benford-Variablen.

Warum viele Datensätze dem NBL folgen

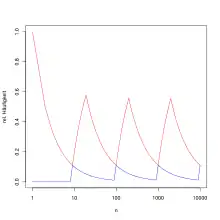
Relative Häufigkeiten der Anfangsziffern 1 (rot) und 9 (blau) unter den Zahlen von 1 bis n: Nur für n = 10^k − 1 stimmen beide überein.

Das NBL gilt für reale Datensätze (damit sind hier solche gemeint, die keinen Manipulationen unterlagen), die genügend umfangreich sind und Zahlen in der Größenordnung von $x$ bis mindestens $10000x$ aufweisen, Daten also, die einigermaßen weit verteilt (dispergiert) sind. Es besagt, dass die Auftretenswahrscheinlichkeit der Ziffernsequenzen in den Zahlen nicht gleichverteilt ist, sondern logarithmischen Gesetzen folgt. Das bedeutet, dass die Auftretenswahrscheinlichkeit einer Ziffernsequenz umso höher ist, je kleiner sie wertmäßig ist und je weiter links sie in der Zahl beginnt. Am häufigsten ist die Anfangssequenz „1“ mit theoretisch 30,103 %. Das NBL beruht auf der Gleichverteilung der Mantissen der Logarithmen der Zahlenwerte des Datensatzes. Der Grund für die erstaunlich weite Gültigkeit des NBL liegt an dem Umstand, dass viele reale Datensätze log-normalverteilt sind, also nicht die Häufigkeiten der Daten selbst, sondern die Größenordnungen dieser Daten einer Normalverteilung folgen. Bei genügend breiter Dispersion der normalverteilten Logarithmen (wenn die Standardabweichung mindestens etwa gleich 0,74 ist) kommt es dazu, dass die Mantissen der Logarithmen stabil einer Gleichverteilung folgen. Ist die Standardabweichung allerdings kleiner, sind auch die Mantissen normalverteilt, und das NBL gilt nicht mehr, zumindest nicht mehr in der dargestellten einfachen Form. Ist die Standardabweichung kleiner als 0,74, kommt es zu dem in der Statistik nicht allzu häufigen Effekt, dass sogar der jeweilige Mittelwert der Normalverteilung der Logarithmen die Auftretenshäufigkeit der Ziffernsequenzen beeinflusst.

Geht man einerseits vom NBL in der heutigen Form aus, so existieren zahlreiche Datensätze, die dem NBL nicht genügen. Andererseits gibt es bereits eine Formulierung des NBL in der Form, dass ihm sämtliche Datensätze genügen.

Das Benfordsche Gesetz gilt insbesondere für Zahlenmaterial, das natürlichen Wachstumsprozessen unterliegt. Dann nämlich verändern sich die Zahlen im Laufe der Zeit und vervielfachen sich. Die erste Position der Mantisse verharrt für ca. 30 % der Zeit auf der 1, 18 % der Zeit auf der 2 usw.: Das entspricht der logarithmischen Verteilung, die das Benfordsche Gesetz vorhersagt, und ist unabhängig von der Zeit, in der eine Vervielfachung erfolgt. Dann beginnt der Zyklus von Neuem bei der 1. Bei einer Momentaufnahme der Preise eines Supermarktes wird man genau diese Verteilung finden, egal wann die Erhebung durchgeführt wird.

Skaleninvarianz

Mit einer Konstanten multiplizierte Datensätze mit Newcomb-Benford-verteilten Anfangsziffern sind wiederum Benford-verteilt. Eine Multiplikation der Daten mit einer Konstanten entspricht der Addition einer Konstanten zu den Logarithmen. Sofern die Daten hinreichend weit verteilt sind, ändert sich dadurch die Verteilung der Mantissen nicht.

Diese Eigenschaft erklärt unmittelbar, warum in Steuererklärungen, Bilanzen etc., oder allgemein bei Datensätzen, deren Zahlen Geldbeträge darstellen, das Newcomb-Benfordsche Gesetz gilt. Wenn es überhaupt eine universell gültige Verteilung der Anfangsziffern in solchen Datensätzen gibt, dann muss diese Verteilung unabhängig davon sein, in welcher Währung die Daten angegeben werden, und die universelle Verteilung darf sich auch durch Inflation nicht verändern. Beides bedeutet, dass die Verteilung skaleninvariant sein muss. Da die Newcomb-Benfordsche Verteilung die einzige ist, die diese Bedingung erfüllt, muss es sich folglich um diese handeln.

Baseninvarianz

Ein Datensatz, der zu einer Basis B₁ dem Benfordschen Gesetz genügt, genügt diesem auch zur Basis B₂. Konkreter gesagt, ein dekadischer Datensatz, der das Benfordsche Gesetz erfüllt, erfüllt das Benfordsche Gesetz auch dann, wenn die dekadischen Zahlen in ein anderes Zahlensystem (z. B. ins binäre, ins oktale oder ins hexadezimale) umgerechnet werden.

Anwendungen

Entsprechen reale Datensätze trotz Erfüllung der parametrischen Anforderungen dem Benfordschen Gesetz insofern nicht, als die Anzahl des Auftretens einer bestimmten Ziffer signifikant von der durch das Benfordsche Gesetz angegebenen Erwartung abweicht, dann wird ein Prüfer jene Datensätze, die mit dieser Ziffer beginnen, einer tiefergehenden Analyse unterziehen, um die Ursache(n) für diese Abweichungen zu finden. Dieses Schnellverfahren kann zu tieferen Erkenntnissen über Besonderheiten des untersuchten Datensatzes bzw. zur Aufdeckung von Manipulationen bei der Datenerstellung führen.

Beispiel

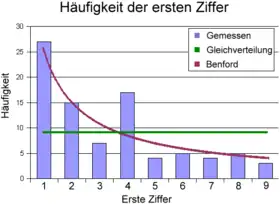
Verteilung der Anfangsziffern einer Tabelle mit 87 Zahlen (siehe Text)

Eine Tabelle berichtet über die Ernteergebnisse aus dem Jahre 2002. Im Diagramm geben die blauen Balken die Häufigkeit der Anfangsziffern der 87 erfassten Zahlen an. Die Benford-Verteilung ist als rote Linie eingezeichnet. Sie spiegelt die Verteilung deutlich besser wider als eine Gleichverteilung (grüne Linie). Trotz der kleinen Stichprobe ist die Bevorzugung kleiner Werte bei der ersten Ziffer erkennbar, ebenso als Tendenz bei der zweiten Ziffer.

Die Tabelle fasst die Ergebnisse zusammen. In der Spalte 1. Ziffer steht, wie oft die Ziffer an erster Stelle auftritt, in der Spalte Benford, wie oft sie nach der Benford-Verteilung dort erwartet wird. Gleiches gilt für die Anzahl der Zahlen mit der Ziffer an zweiter Stelle in der Spalte 2. Ziffer. Die Ziffer 1 tritt danach 27-mal an erster Stelle auf, erwartet war 26,19-mal. Die Ziffer 4 steht 17-mal an erster Stelle, nach Benford sollte sie im Mittel 8,43-mal auftreten.

Mit abnehmendem Stellenwert der Ziffer nähert sich die oben angegebene Benford-Verteilung immer mehr der Gleichverteilung der Ziffern.

Ziffer	1. Ziffer	Benford	2. Ziffer	Benford
0	—	—	9	10,41
1	27	26,19	17	9,91
2	15	15,32	9	9,47
3	7	10,87	11	9,08
4	17	8,43	5	8,73
5	4	6,89	9	8,41
6	5	5,82	7	8,12
7	4	5,05	8	7,86
8	5	4,45	7	7,62
9	3	3,98	5	7,39
Summe	87		87

In der Wirtschaft

Das Benfordsche Gesetz findet Anwendung bei der Aufdeckung von Betrug bei der Bilanzerstellung, der Fälschung in Abrechnungen und generell zum raschen Auffinden eklatanter Unregelmäßigkeiten im Rechnungswesen. Mit Hilfe des Benfordschen Gesetzes wurde das bemerkenswert „kreative“ Rechnungswesen bei Enron und Worldcom aufgedeckt, durch welches das Management die Anleger um ihre Einlagen betrogen hatte (→ Wirtschaftskriminalität). Heute benutzen Wirtschaftsprüfer und Steuerfahnder Methoden, die auf dem Benfordschen Gesetz beruhen. Diese Methoden stellen einen wichtigen Teil der mathematisch-statistischen Methoden dar, die seit mehreren Jahren zur Aufdeckung von Bilanzfälschung, Steuer- und Investorenbetrug und allgemein Datenbetrug in Verwendung sind. Es konnte weiter gezeigt werden, dass auch die führenden Ziffern der Marktpreise dem Benfordschen Gesetz folgen.[1] Auch die Manipulation der Wirtschaftsdaten Griechenlands ließ sich mit dem Benfordschen Gesetz nachweisen.[2]

In der Forschung

Das Benfordsche Gesetz kann auch bei der Aufdeckung von Datenfälschung in der Wissenschaft helfen. Es waren Datensätze aus den Naturwissenschaften, die zum Benfordschen Gesetz führten. Karl-Heinz Tödter vom Forschungszentrum der Deutschen Bundesbank hat dasselbe Gesetz benutzt, um in einem Beitrag zum German Economic Review die Ergebnisse von 117 volkswirtschaftlichen Arbeiten zu überprüfen.[3]

Wahlen

Politikwissenschaftler untersuchten mit Hilfe des Benfordschen Gesetzes Wahlergebnisse mehrerer Bundestagswahlen (der Jahre 1990–2005) auf Wahlkreisebene und stießen vereinzelt (4 Fälle in 1500 Tests) auf signifikante Unregelmäßigkeiten die Erststimme betreffend. Bei der Betrachtung der Zweitstimme, also der direkten Parteiwahl, wurden jedoch in 51 von 190 Tests Unregelmäßigkeiten beobachtet.[4] Laut dem Studienautor Achim Goerres ist dieses Ergebnis kein Hinweis auf Manipulationen.[5]

Es konnten auch Hinweise auf mögliche Fälschungen im Rahmen der Präsidentschaftswahlen 2009 im Iran gefunden werden.[6]

Andere Experten halten das Benfordsche Gesetz für nur beschränkt geeignet zur Untersuchung von Wahlen.[7][8][9]

Größe der Städte in Deutschland

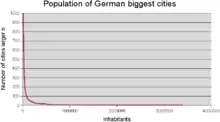
Verteilung der Größe deutscher Großstädte

Die rechte Abbildung zeigt die Größenverteilung deutscher Städte. Der Grafik hinterlegt sind die Einwohnerzahlen der 998 größten Städte.[10] Eine Benford-Analyse liefert folgende Häufigkeiten der Anfangsziffern:

Ziffer	Gemessen	Erwartet
1	340	300,4
2	320	175,7
3	133	124,7
4	87	96,7
5	50	79,0
6	24	66,8
7	20	57,9
8	12	51,1
9	12	45,7

Die Häufigkeit der Ziffern 3 und 4 entsprechen der Erwartung. Hingegen tritt die Zahl 1 vermehrt auf. Besonders ausgeprägt ist die Abweichung der Ziffer 2 auf Kosten der nur selten an erster Stelle beobachteten Ziffern 7, 8 und 9.

Dieses Beispiel zeigt wiederum, dass Datensätze bestimmte Voraussetzungen erfüllen müssen, um dem NBL zu genügen; der vorliegende Datensatz tut dies nicht. Grund hierfür ist die Beschränkung auf Städte, die Verteilung aller Gemeinden dürfte eine genauere Übereinstimmung ergeben. Zudem gibt es eine natürliche Mindestsiedlungsgröße, ebenso haben Gemeindezusammenlegungen Einfluss auf die Verteilung. Kurioserweise gehören sogar etwa 50 % der Beispiele, die Benford in seiner Publikation als Belege für das NBL anführte, zu der Klasse von Datensätzen, die keine Benford-verteilten Anfangsziffern, sondern eine höchstens im Groben ähnliche Verteilung der Anfangsziffern aufweisen.

Signifikanz

Wie groß die Abweichungen der beobachteten Verteilung von der theoretisch zu erwartenden Verteilung mindestens sein müssen, damit ein begründeter Verdacht auf Manipulation als erhärtet angesehen werden kann, wird mit Hilfe mathematisch-statistischer Methoden (z. B. dem Chi-Quadrat-Test oder dem Kolmogorow-Smirnow-Test, „KS-Test“) bestimmt. Für den $\chi ^{2}$ -Test sollte beim Test von überzufälligen Abweichungen bei der Anfangsziffer eine Stichprobe ab 109 Zahlen genügen ( $n\cdot 0{,}046\geq 5$ ist erfüllt für alle $n\geq 109$ ). Sind die Stichproben viel kleiner, sind die Ergebnisse des Chi-Quadrat-Tests anfechtbar und der KS-Test gegebenenfalls zu tolerant. In einem solchen Fall kann z. B. auf einen sehr aufwändigen, aber exakten Test auf Basis der Multinomialverteilung zurückgegriffen werden. Außerdem müssen die Daten des Datensatzes voneinander statistisch unabhängig sein. (Daher können Zahlen z. B. der Fibonacci-Folge nicht mit dem Chi-Quadrat-Anpassungs-Test auf Signifikanz getestet werden, da das sich ergebende Resultat unzuverlässig wird.)

Dass sich gerade Saldenlisten, Rechnungslisten und ähnliche Aufstellungen gemäß dem Benfordschen Gesetz verhalten, liegt an dem Umstand, dass es sich bei der Mehrzahl solcher Zahlenreihen um Sammlungen von Zahlen handelt, die die unterschiedlichsten arithmetischen Prozesse durchlaufen haben und sich daher wie Quasi-Zufallszahlen verhalten. Lässt man den geschäftlichen und buchungstechnischen Prozessen freien Lauf, dann wirken ab einer gewissen Geschäftsgröße die Gesetze des Zufalls und es gilt mithin auch das Benfordsche Gesetz. Wird allerdings im Verlauf einer Rechnungsperiode konsequent Einfluss auf diese Zahlen genommen, indem man häufig welche schönt, bestimmte Zahlen verschwinden lässt oder welche hinzu erfindet oder wegen gegebener Kompetenzbeschränkungen sogar Prozesse manipuliert, dann wird der Zufall merklich gestört. Diese Störungen manifestieren sich in signifikanten Abweichungen von der theoretisch zu erwartenden Ziffernverteilung.

In der Praxis wird häufig festgestellt, dass die herkömmlichen Signifikanztests bei Benford-Analysen nicht ganz zuverlässig sind. Zudem sind bisweilen die Daten eines Datensatzes nicht völlig unabhängig voneinander, weshalb man für solche Datensätze z. B. den Chi-Quadrat-Test nicht verwenden darf. An der Entwicklung von an das NBL besser angepassten Signifikanztests wird gearbeitet.

Beispiel: Wenn ein Angestellter Bestellungen bis zu 1000 EUR ohne Genehmigung der Geschäftsleitung durchführen darf und er bei Vorliegen von Angeboten höher als 1000 EUR die Bestellungen häufig auf mehrere kleinere Posten aufteilt, um sich die Mühen der Genehmigung zu ersparen, dann finden sich in der Benford-Verteilung der Bestellbeträge signifikante Abweichungen von der theoretischen Erwartung.

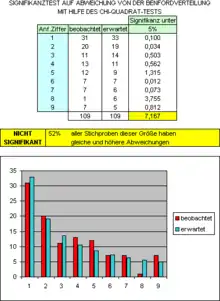
Signifikanztest auf Abweichung von der Benford-Verteilung mit Hilfe des Chi-Quadrat-Tests

Dieses Beispiel zeigt aber auch, dass statistische Methoden einzelne Unregelmäßigkeiten nicht aufdecken können. Eine gewisse Konsequenz der Manipulationen ist erforderlich. Je größer die Stichprobe ist, umso empfindlicher reagiert ein Signifikanztest im Allgemeinen auf Manipulationen.

Test auf signifikante Abweichungen

Benford-Analysen werden für die einfachsten Analysen der mathematischen Statistik gehalten. Das nachstehende Beispiel ist das Ergebnis der Auszählung der Anfangsziffern einer Stichprobe von 109 Summen aus einer Aufstellung. Die realen (beobachteten) Auszählungsergebnisse werden mit den bei 109 Anfangsziffern zu erwartenden Auszählungsergebnissen verglichen und mittels Chi-Quadrat-Test dahingehend untersucht, ob die gefundenen Abweichungen zufällig sein können oder durch Zufall allein nicht mehr zu erklären sind. Als Entscheidungskriterium wird in diesem Beispiel angenommen, dass von Überzufälligkeit auszugehen ist, wenn die Wahrscheinlichkeit für das zufällige Auftreten der beobachteten Verteilung oder einer mindestens genauso unwahrscheinlichen kleiner oder gleich 5 % ist (statistischer Test). Da in unserem Beispiel 52 % aller Verteilungen diese oder höhere Abweichungen aufweisen, wird ein Prüfer die Hypothese, dass die Abweichungen durch Zufall entstanden sind, nicht verwerfen.

Tiefergehende Benford-Analysen

Liegen sehr lange Listen mit mehreren tausend Zahlen vor, ist ein Benford-Test nicht nur mit der Anfangsziffer durchführbar. Eine solche Datenfülle erlaubt es, auch die 2., die 3., die Summe 1. + 2., eventuell sogar die Summe 1. + 2. + 3. Ziffer simultan zu überprüfen (für diese sollte man allerdings mindestens 11.500 Zahlen haben, da anderenfalls der Chi-Quadrat-Test unsichere Ergebnisse bringen könnte). Für diese Prüfungen existieren ebenfalls Benford-Verteilungen, wenngleich sie auch etwas umfangreicher sind. So z. B. beträgt die theoretische Erwartung für das Erscheinen der Anfangsziffern 123… 0,35166 %, wohingegen nur noch 0,13508 % aller Zahlen die Anfangsziffern 321… aufweisen.

Stets gilt die Regel, dass die Ziffern umso mehr einer Gleichverteilung folgen, je kleiner ihr Stellenwert ist. Cent-Beträge folgen nahezu exakt einer Gleichverteilung, wodurch sich bei Cent-Beträgen der logarithmische Ansatz im Allgemeinen erübrigt. Bei sehr kleinen Währungen werden Tests auf Gleichverteilung der Scheidemünzenbeträge (z. B. Kopeke-RUS, Heller-CZ, Fillér-H, Lipa-HR) unscharf, da in der Praxis sehr häufig gerundet wird. Große Währungen (US-Dollar, Pfund-Sterling, Euro) erlauben solche Tests aber zumeist schon.

Schätzung und Planung von Unternehmensumsätzen

Das Benfordsche Gesetz lässt sich auch zur Schätzung von Umsatzziffern von Unternehmen heranziehen. Für die Logarithmen aller Fakturenbeträge eines Unternehmens wird angenommen, dass sie annähernd einer Normalverteilung folgen. Die Anfangsziffern der Fakturenbeträge folgen somit der Benford-Verteilung mit Erwartungswert von etwa 3,91. Der Abstand zwischen dem Logarithmus des kleinsten und dem Logarithmus des größten Fakturenbetrages repräsentiert annähernd die 6-fache Standardabweichung der Normalverteilung der Logarithmen. Mit der Kenntnis des höchsten Fakturenbetrages und der Anzahl der gültigen Fakturen, aus welchen sich der zu schätzende Umsatz zusammensetzt, ist eine brauchbare Schätzung des Umsatzes möglich, wie nachstehendes Beispiel aus der Praxis zeigt. Der Stellenwert in der Tabelle bezeichnet die Ziffer vor dem Komma des Logarithmus. Der tatsächliche Umsatz lag bei 3,2 Mio. Währungseinheiten. So nahe am tatsächlichen Ergebnis liegt man bei Umsatzschätzungen allerdings nicht immer. Wenn die Annahme der Normalverteilung für die Größenordnungen nicht zutrifft, muss man eine Schätzverteilung wählen, die der realen eher gleicht. Zumeist folgen die Größenordnungen der Fakturenbeträge dann einer Logarithmischen Normalverteilung.

Schätzung Gesamtumsatz

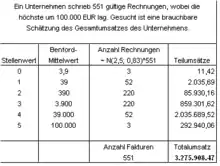
Zwar wird die tatsächliche Verteilung der Fakturenbeträge immer nur zufällig mit jener der Schätzung übereinstimmen, die Summe aller Schätzfehler je Stellenwert kompensiert sich jedoch fast immer auf einen eher kleinen Betrag.

Auch im Rahmen der Planung von Unternehmensumsätzen kann dieses Verfahren zur Überprüfung der Plausibilität von Planumsätzen, die zumeist als Ergebnis von Schätzungen und Hochrechnungen von Erfahrungswerten verkaufsorientierter Abteilungen entstanden sind, eingesetzt werden, indem man eruiert, wie viele Fakturen zur Erreichung des angegebenen Umsatzes erwartet werden und wie hoch der höchste Fakturenbetrag sein wird. Oft zeigt diese Analyse, dass auf solche Schätzwerte, die der Planung zugrunde gelegt werden, kein allzu großer Verlass ist. Die Benfordanalyse gibt der Verkaufsabteilung dann das Feedback zur realitätsbezogenen Korrektur ihrer Erwartungen.

Unterstellt man, dass die Logarithmen der einzelnen Umsätze gleichverteilt sind, so sind die Umsätze quasi „logarithmisch gleichverteilt“. Die Dichtefunktion der Umsätze hat dann ein Histogramm, das bei geeigneter Klasseneinteilung der Verteilung der Ziffernsequenzen (z. B. neun Klassen, verglichen mit First Digit) der Benford-Verteilung sehr ähnlich sieht.

Erzeugung Benford-verteilter Anfangsziffern

Die Erzeugung von praktisch zufälligen Zahlen mit Benford-verteilten Anfangsziffern ist mit dem PC recht einfach möglich.

Gleichverteilte Zahlen

Die Funktion $y=10^{k}$ erzeugt Zahlen mit Benford-verteilten Anfangsziffern für $k=r+s$ . Dabei ist $r$ eine zufällige gleichverteilte positive ganze Zahl aus einem festen Intervall, und $s$ ist eine gleichverteilte Zufallszahl zwischen 0 und 1. Anstelle von $10$ kann aufgrund der Baseninvarianz auch jede andere positive Zahl verwendet werden.

Normalverteilte Zahlen

Die Funktion $y=r^{2}\cdot \tan ^{2}(t)$ erzeugt für $0\leq t<{\tfrac {1}{2}}\pi$ , mit $t$ als gleichverteilter Zufallsvariablen, Zahlen mit etwa normalverteilten Größenordnungen von $y$ und Benford-verteilten Anfangsziffern. Für praktische Zwecke sollte $r$ relativ hoch gewählt werden $(r>1000)$ . Ist $r<1000$ , erkennt man mit sinkendem $r$ , dass die Verteilung der Zahlen der Form einer Lognormalverteilung ähnelt. Ist $r<50$ , sind die erzeugten Anfangsziffern der Zahlen im Allgemeinen nicht mehr Benford-verteilt. Für Anwendungen in der Praxis ist die breite Streuung der Größenordnungen von $y$ , die das Quadrat der Tangensfunktion – noch dazu bei großen $r$ – erzeugt, in vielen Fällen nicht optimal.

Literatur

F. Benford: The Law of Anomalous Numbers. In: Proceedings of the American Philosophical Society (Proc. Amer. Phil. Soc.). Philadelphia 78.1938, S. 551–572. ISSN 0003-049X
Simon Newcomb: Note on the Frequency of the Use of different Digits in Natural Numbers. In: American journal of mathematics (Amer. J. Math.). Baltimore 4.1881, S. 39–40, ISSN 0002-9327.
Mark J. Nigrini: The Detection of Income Tax Evasion Through an Analysis of Digital Frequencies. Dissertation. University of Cincinnati. UMI, Ann Arbor Mich 1992. (Mikrofiche).
Ian Stewart: Das Gesetz der ersten Ziffer. In: Spektrum der Wissenschaft, Heidelberg 1994,4 (Apr.), S. 16 ff., ISSN 0170-2971.
H. Rafeld: Digitale Ziffernanalyse mit Benford’s Law zur Deliktrevision doloser Handlungen. Diplomarbeit. Berufsakademie Ravensburg, Ravensburg 2003.
Peter N. Posch: Ziffernanalyse in Theorie und Praxis – Testverfahren zur Fälschungsaufspürung mit Benfords Gesetz. 2. Auflage. Europäische Wirtschaft, Berlin 2005, ISBN 3-8322-4492-1.
Tarek el Sehity, Erik Hoelzl, Erich Kirchler: Price developments after a nominal shock, Benford’s Law and psychological pricing after the euro introduction. In: International Journal of Research in Marketing. 22 Amsterdam 2005, Nr. 4, Dezember 2005, S. 471–480, doi:10.1016/j.ijresmar.2005.09.002, ISSN 0167-8116.
S. Günnel, K.-H. Tödter: Does Benford’s law hold in economic research and forecasting? (Memento vom 17. Oktober 2010 im Internet Archive). (PDF) In: Deutsche Bundesbank Discussion Paper. Series 1. Economic Studies. Frankfurt am Main 32/2007.
H. Rafeld, F. Then Bergh: Digitale Ziffernanalyse in deutschen Rechnungslegungsdaten. In: Zeitschrift Interne Revision, Berlin 42.2007,1, S. 26–33, ISSN 0044-3816.
Arno Berger, Theodore Hill: Benford’s law strikes back: no simple explanation in sight for mathematical gem. In: Mathematical Intelligencer. 2011, Nr. 1, S. 85–91.
Arno Berger, Theodore Hill: What is Benfords Law? (PDF; 126 kB) Notices AMS, Februar 2017 (PDF; 126 kB).
Ehrhard Behrends: Das Benfordsche Gesetz oder warum die Ziffer 1 häufiger am Anfang steht. In: Die Welt. 4. April 2005.
Zhaodong Cai, Matthew Faust, A. J. Hildebrand, Junxian Li, Yuan Z: The surprising accuracy of Benford's law in Mathematics, American Mathematical Monthly, Band 127, 2020, S. 217–237 (erhielt den Lester Randolph Ford Award 2021)

Weblinks

Überblick über Benfords Gesetz und weiterführende Linksammlung
Ein didaktisch aufbereiteter Artikel zu Benfords Gesetz. (Memento vom 1. November 2012 im Internet Archive).
Eric W. Weisstein: Benford’s Law. In: MathWorld (englisch).
Adrian Lobe: Mit Mathematik gegen Schwindler. In: Die Presse. 9. September 2011.
Brigitte Röthlein: Alle Welt liebt die Eins. (Memento vom 25. November 2015 im Internet Archive). In: Berliner-Zeitung.de. 15. Juni 2007.
The Benford Online Bibliography (englisch).
Peter N. Posch: Gesetz der ungewöhnlichen Zahlen. In: FiFo Ost, 25. August 2010.
Testing Benford’s Law in OLAP Cubes. Kalkulation für Microsoft Analysis Services (englisch).
Chapter 34: Explaining Benford's Law in The Scientist and Engineer's Guide to Digital Signal Processing, Steven Smith, ISBN 978-0966017632

Einzelnachweise

Tarek el Sehity, Erik Hoelzl, Erich Kirchler: Price developments after a nominal shock, Benford’s Law and psychological pricing after the euro introduction. In: International Journal of Research in Marketing, 22, Amsterdam 2005, Nr. 4, Dezember 2005, S. 471–480, doi:10.1016/j.ijresmar.2005.09.002
Griechenland hat nachweislich geschummelt - Wissenschaftler der TU Ilmenau weist Zahlenschummelei Griechenlands nach. Bereits die Aufnahme Griechenlands in den Euro-Raum erfolgte mit gefälschten Bilanzen. The Epoch Times vom 31. Oktober 2011
Hans Christian Müller: Auf der Jagd nach Zahlen-Fälschern. In: Handelsblatt, 30. November 2009.
Christian Breunig, Achim Goerres: Searching for electoral irregularities in an established democracy: Applying Benford’s Law tests to Bundestag elections in Unified Germany. In: Electoral Studies (= Special Symposium on the Politics of Economic Crisis). Band 30, Nr. 3, 1. September 2011, S. 534–545, doi:10.1016/j.electstud.2011.03.005 (mpg.de [PDF; abgerufen am 10. September 2021]).
Doku im Ersten, Erstsendung im ARD-Hauptprogramm am 6. September 2021: Wie wir im Wahlkampf manipuliert werden, Zeitindex 15:27 bis 16:01, erhältlich in der ARD Mediathek.
Boudewijn F. Roukema: Benford’s Law anomalies in the 2009 Iranian presidential election. arxiv:0906.2789v1.
Joseph Deckert, Mikhail Myagkov und Peter C. Ordeshook: The Irrelevance of Benford’s Law for Detecting Fraud in Elections. (PDF) Caltech/MIT Voting Technology Project Working Paper No. 9, 2010 (bei archive.org (Memento vom 17. Mai 2014 im Internet Archive)).
Charles R. Tolle, Joanne L. Budzien, Randall A. LaViolette: Do dynamical systems follow Benford’s Law? In: Chaos, 10, 2, 2000, S. 331–336, doi:10.1063/1.166498.
Joseph Deckert, Mikhail Myagkov, and Peter C. Ordeshook: Benford’s Law and the Detection of Election Fraud. University of Oregon 97403 and California Institute of Technology 91124, 2011, abgerufen am 7. November 2020 (englisch): „With respect to Benford’s Law, we know some of the conditions that, if satisfied, yield numbers in accordance with it, but just as there is no basis for supposing that the Ijiri-Simon model of firm size or an empirical relationship that holds for insects and city sizes applies to parties, candidates or anything else political, there is no reason to suppose a priori that the conditions sufficient to occasion digits matching 2BL necessarily hold any meaning for elections.“
[https://de.wikipedia.org/w/index.php?title=Wikipedia:Defekte_Weblinks&dwl=http://bevoelkerungsstatistik.de/ Seite nicht mehr abrufbar], Suche in Webarchiven: @1@2[http://timetravel.mementoweb.org/list/2010/http://bevoelkerungsstatistik.de/ ]

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Tarek el Sehity, Erik Hoelzl, Erich Kirchler: Price developments after a nominal shock, Benford’s Law and psychological pricing after the euro introduction. In: International Journal of Research in Marketing, 22, Amsterdam 2005, Nr. 4, Dezember 2005, S. 471–480, doi:10.1016/j.ijresmar.2005.09.002

[2] Griechenland hat nachweislich geschummelt - Wissenschaftler der TU Ilmenau weist Zahlenschummelei Griechenlands nach. Bereits die Aufnahme Griechenlands in den Euro-Raum erfolgte mit gefälschten Bilanzen. The Epoch Times vom 31. Oktober 2011

[3] Hans Christian Müller: Auf der Jagd nach Zahlen-Fälschern. In: Handelsblatt, 30. November 2009.

[4] Christian Breunig, Achim Goerres: Searching for electoral irregularities in an established democracy: Applying Benford’s Law tests to Bundestag elections in Unified Germany. In: Electoral Studies (= Special Symposium on the Politics of Economic Crisis). Band 30, Nr. 3, 1. September 2011, S. 534–545, doi:10.1016/j.electstud.2011.03.005 (mpg.de [PDF; abgerufen am 10. September 2021]).

[5] Doku im Ersten, Erstsendung im ARD-Hauptprogramm am 6. September 2021: Wie wir im Wahlkampf manipuliert werden, Zeitindex 15:27 bis 16:01, erhältlich in der ARD Mediathek.

[6] Boudewijn F. Roukema: Benford’s Law anomalies in the 2009 Iranian presidential election. arxiv:0906.2789v1.

[7] Joseph Deckert, Mikhail Myagkov und Peter C. Ordeshook: The Irrelevance of Benford’s Law for Detecting Fraud in Elections. (PDF) Caltech/MIT Voting Technology Project Working Paper No. 9, 2010 (bei archive.org (Memento vom 17. Mai 2014 im Internet Archive)).

[8] Charles R. Tolle, Joanne L. Budzien, Randall A. LaViolette: Do dynamical systems follow Benford’s Law? In: Chaos, 10, 2, 2000, S. 331–336, doi:10.1063/1.166498.

[9] Joseph Deckert, Mikhail Myagkov, and Peter C. Ordeshook: Benford’s Law and the Detection of Election Fraud. University of Oregon 97403 and California Institute of Technology 91124, 2011, abgerufen am 7. November 2020 (englisch): „With respect to Benford’s Law, we know some of the conditions that, if satisfied, yield numbers in accordance with it, but just as there is no basis for supposing that the Ijiri-Simon model of firm size or an empirical relationship that holds for insects and city sizes applies to parties, candidates or anything else political, there is no reason to suppose a priori that the conditions sufficient to occasion digits matching 2BL necessarily hold any meaning for elections.“

[10] [https://de.wikipedia.org/w/index.php?title=Wikipedia:Defekte_Weblinks&dwl=http://bevoelkerungsstatistik.de/ Seite nicht mehr abrufbar], Suche in Webarchiven: @1@2[http://timetravel.mementoweb.org/list/2010/http://bevoelkerungsstatistik.de/ ]