Kovarianzmatrix

In der Stochastik ist die Kovarianzmatrix die Verallgemeinerung der Varianz einer eindimensionalen Zufallsvariable auf eine mehrdimensionale Zufallsvariable, d. h. auf einen Zufallsvektor. Die Elemente auf der Hauptdiagonalen der Kovarianzmatrix stellen die jeweiligen Varianzen dar, und alle übrigen Elemente Kovarianzen. Die Kovarianzmatrix wird auch Varianz-Kovarianzmatrix oder selten Streuungsmatrix bzw. Dispersionsmatrix (lateinisch dispersio „Zerstreuung“, von dispergere „verteilen, ausbreiten, zerstreuen“) genannt und ist eine positiv semidefinite Matrix. Sind alle Komponenten des Zufallsvektors ${\displaystyle \mathbf {X} }$ linear unabhängig, so ist die Kovarianzmatrix positiv definit.

Eine um ${\displaystyle (0;0)}$ zentrierte zweidimensionale Gauß-Verteilung, mit der Kovarianzmatrix ${\displaystyle \mathbf {\Sigma } ={\begin{pmatrix}1&0{,}5\\0{,}5&1\end{pmatrix}}}$

Definition

Sei ${\displaystyle \mathbf {X} }$ ein Zufallsvektor

${\displaystyle \mathbf {X} ={\begin{pmatrix}X_{1}\\X_{2}\\\vdots \\X_{n}\end{pmatrix}}}$,

wobei ${\displaystyle \operatorname {E} (X_{i})=\mu _{i}}$ den Erwartungswert von ${\displaystyle X_{i}}$, ${\displaystyle \operatorname {Var} (X_{i})=\sigma _{i}^{2}}$ die Varianz von ${\displaystyle X_{i}}$ und ${\displaystyle \operatorname {Cov} (X_{i},X_{j})=\sigma _{ij}\;,i\neq j}$ die Kovarianz der reellen Zufallsvariablen ${\displaystyle X_{i}}$ und ${\displaystyle X_{j}}$ darstellt. Der Erwartungswertvektor von ${\displaystyle \mathbf {X} }$ ist dann gegeben durch (siehe Erwartungswert von Matrizen und Vektoren)

${\displaystyle \operatorname {E} (\mathbf {X} )=\operatorname {E} {\begin{pmatrix}X_{1}\\X_{2}\\\vdots \\X_{n}\end{pmatrix}}={\begin{pmatrix}\mu _{1}\\\mu _{2}\\\vdots \\\mu _{n}\end{pmatrix}}={\boldsymbol {\mu }}}$,

d. h. der Erwartungswert des Zufallsvektors ist der Vektor der Erwartungswerte. Eine Kovarianzmatrix für den Zufallsvektor ${\displaystyle \mathbf {X} }$ lässt sich wie folgt definieren:[1]

${\displaystyle {\begin{aligned}\operatorname {Cov} (\mathbf {X} )&=\operatorname {E} \left((\mathbf {X} -{\boldsymbol {\mu }})(\mathbf {X} -{\boldsymbol {\mu }})^{\top }\right)\\\\&=\operatorname {E} {\begin{pmatrix}(X_{1}-\mu _{1})^{2}&(X_{1}-\mu _{1})(X_{2}-\mu _{2})&\cdots &(X_{1}-\mu _{1})(X_{n}-\mu _{n})\\\\(X_{2}-\mu _{2})(X_{1}-\mu _{1})&(X_{2}-\mu _{2})^{2}&\cdots &(X_{2}-\mu _{2})(X_{n}-\mu _{n})\\\\\vdots &\vdots &\ddots &\vdots \\\\(X_{n}-\mu _{n})(X_{1}-\mu _{1})&(X_{n}-\mu _{n})(X_{2}-\mu _{2})&\cdots &(X_{n}-\mu _{n})^{2}\end{pmatrix}}\\\\&={\begin{pmatrix}\operatorname {Var} (X_{1})&\operatorname {Cov} (X_{1},X_{2})&\cdots &\operatorname {Cov} (X_{1},X_{n})\\\\\operatorname {Cov} (X_{2},X_{1})&\operatorname {Var} (X_{2})&\cdots &\operatorname {Cov} (X_{2},X_{n})\\\\\vdots &\vdots &\ddots &\vdots \\\\\operatorname {Cov} (X_{n},X_{1})&\operatorname {Cov} (X_{n},X_{2})&\cdots &\operatorname {Var} (X_{n})\end{pmatrix}}\\\\&={\begin{pmatrix}\sigma _{1}^{2}&\sigma _{12}&\cdots &\sigma _{1n}\\\\\sigma _{21}&\sigma _{2}^{2}&\cdots &\sigma _{2n}\\\\\vdots &\vdots &\ddots &\vdots \\\\\sigma _{n1}&\sigma _{n2}&\cdots &\sigma _{n}^{2}\end{pmatrix}}\\\\&=\mathbf {\Sigma } \end{aligned}}}$

Die Kovarianzmatrix wird mit ${\displaystyle \operatorname {Cov} (\mathbf {X} )}$, oder ${\displaystyle \mathbf {\Sigma } _{X}}$ notiert und die Kovarianzmatrix der asymptotischen Verteilung einer Zufallsvariablen mit ${\displaystyle {\boldsymbol {\operatorname {V} }}}$ oder ${\displaystyle {\overline {\boldsymbol {\operatorname {V} }}}}$. Die Kovarianzmatrix und der Erwartungswertvektor sind die wichtigsten Kenngrößen einer Wahrscheinlichkeitsverteilung. Sie werden bei einer Zufallsvariablen als Zusatzinformationen wie folgt angegeben: ${\displaystyle X\;\sim \;({\boldsymbol {\mu }},\mathbf {\Sigma } )}$. Die Kovarianzmatrix als Matrix aller paarweisen Kovarianzen der Elemente des Zufallsvektors enthält Informationen über seine Streuung und über Korrelationen zwischen seinen Komponenten. Wenn keine der Zufallsvariablen ${\displaystyle X_{1},\ldots ,X_{n}}$ degeneriert ist (d. h. wenn keine von ihnen eine Varianz von Null aufweist) und kein exakter linearer Zusammenhang zwischen den ${\displaystyle X_{i}}$ vorliegt, dann ist die Kovarianzmatrix positiv definit.[2] Man spricht außerdem von einer skalaren Kovarianzmatrix, wenn alle Außerdiagonaleinträge der Matrix Null sind und die Diagonalelemente dieselbe positive Konstante darstellen.[3]

Eigenschaften

Grundlegende Eigenschaften

• Für ${\displaystyle i=j}$ gilt: ${\displaystyle \operatorname {Cov} (X_{i},X_{j})=\operatorname {Var} (X_{i})}$. Somit enthält die Kovarianzmatrix auf der Hauptdiagonalen die Varianzen der einzelnen Komponenten des Zufallsvektors. Alle Elemente auf der Hauptdiagonalen sind daher nichtnegativ.
• Eine reelle Kovarianzmatrix ist symmetrisch, da die Kovarianz zweier Zufallsvariablen symmetrisch ist.
• Die Kovarianzmatrix ist positiv semidefinit: Aufgrund der Symmetrie ist jede Kovarianzmatrix mittels Hauptachsentransformation diagonalisierbar, wobei die Diagonalmatrix wieder eine Kovarianzmatrix ist. Da auf der Diagonale nur Varianzen stehen, ist die Diagonalmatrix folglich positiv semidefinit und somit auch die ursprüngliche Kovarianzmatrix.
• Umgekehrt kann jede symmetrische positiv semidefinite ${\displaystyle d\times d}$-Matrix als Kovarianzmatrix eines ${\displaystyle d}$-dimensionalen Zufallsvektors aufgefasst werden.
• Aufgrund der Diagonalisierbarkeit, wobei die Eigenwerte (auf der Diagonale) wegen der positiven Semidefinitheit nicht-negativ sind, können Kovarianzmatrizen als Ellipsoide dargestellt werden.
• Für alle Matrizen ${\displaystyle \mathbf {A} \in \mathbb {R} ^{m\times n}}$ gilt ${\displaystyle \operatorname {Cov} (\mathbf {A} \mathbf {X} )=\operatorname {E} {\Big (}\mathbf {A} (\mathbf {X} -\operatorname {E} (\mathbf {X} ))(\mathbf {X} -\operatorname {E} (\mathbf {X} ))^{\top }\mathbf {A} ^{\top }{\Big )}=\mathbf {A} \operatorname {Cov} (\mathbf {X} )\ \mathbf {A} ^{\top }}$.
• Für alle Vektoren ${\displaystyle \mathbf {b} \in \mathbb {R} ^{n}}$ gilt ${\displaystyle \operatorname {Cov} (\mathbf {X} +\mathbf {b} )=\operatorname {Cov} (\mathbf {X} )}$.
• Sind ${\displaystyle \mathbf {X} }$ und ${\displaystyle \mathbf {Y} }$ unkorrelierte Zufallsvektoren, dann gilt ${\displaystyle \operatorname {Cov} (\mathbf {X} +\mathbf {Y} )=\operatorname {Cov} (\mathbf {X} )+\operatorname {Cov} (\mathbf {Y} )}$.
• Man erhält mit der Diagonalmatrix ${\displaystyle \mathbf {D} =\left(\operatorname {diag} ({\boldsymbol {\Sigma }})\right)^{1/2}=\operatorname {diag} (\sigma _{1},\sigma _{2},\dotsc ,\sigma _{n})}$ die Kovarianzmatrix durch die Beziehung ${\displaystyle {\boldsymbol {\Sigma }}=\mathbf {D} \,\mathbf {P} \,\mathbf {D} }$, wobei ${\displaystyle \mathbf {P} }$ die Korrelationsmatrix in der Grundgesamtheit darstellt
• Sind die Zufallsvariablen standardisiert, so enthält die Kovarianzmatrix gerade die Korrelationskoeffizienten und man erhält die Korrelationsmatrix
• Die Inverse der Kovarianzmatrix ${\displaystyle \mathbf {P} =\mathbf {\Sigma } ^{-1}}$ heißt Präzisions­matrix oder Konzentrationsmatrix
• Die Determinante der Kovarianzmatrix ${\displaystyle {\begin{vmatrix}\mathbf {\Sigma } \end{vmatrix}}}$ wird verallgemeinerte Varianz genannt und ist ein Maß für die Gesamtstreuung eines multivariaten Datensatzes
• Für die Spur der Kovarianzmatrix gilt ${\displaystyle \operatorname {Spur} (\mathbf {\Sigma } )=\sum \nolimits _{i=1}^{n}\sigma _{i}^{2}}$
• ${\displaystyle \operatorname {Cov} (\mathbf {X} +\mathbf {Y} ,\mathbf {Z} )=\operatorname {Cov} (\mathbf {X} ,\mathbf {Z} )+\operatorname {Cov} (\mathbf {Y} ,\mathbf {Z} )}$

Beziehung zum Erwartungswert des Zufallsvektors

Ist ${\displaystyle {\boldsymbol {\mu }}=\operatorname {E} (\mathbf {X} )}$ der Erwartungswertvektor, so lässt sich mit dem Verschiebungssatz von Steiner angewandt auf mehrdimensionale Zufallsvariablen zeigen, dass

${\displaystyle {\begin{aligned}\operatorname {Cov} (\mathbf {X} )&=\operatorname {E} {\bigl (}(\mathbf {X} -{\boldsymbol {\mu }})(\mathbf {X} -{\boldsymbol {\mu }})^{\top }{\bigr )}\\&=\operatorname {E} (\mathbf {X} \mathbf {X} ^{\top })-{\boldsymbol {\mu }}{\boldsymbol {\boldsymbol {\mu }}}^{\top }\end{aligned}}}$.

Hierbei s​ind Erwartungswerte v​on Vektoren u​nd Matrizen komponentenweise z​u verstehen.

Ein Zufallsvektor, der einer gegebenen Kovarianzmatrix gehorchen und den Erwartungswert ${\displaystyle {\boldsymbol {\mu }}}$ haben soll, kann wie folgt simuliert werden:
zunächst ist die Kovarianzmatrix zu zerlegen (z. B. mit der Cholesky-Zerlegung):

${\displaystyle \operatorname {Cov} (\mathbf {X} )=\mathbf {D} \mathbf {D} ^{\top }}$.

Anschließend lässt s​ich der Zufallsvektor berechnen zu

${\displaystyle \mathbf {X} =\mathbf {D} \mathbf {\xi } +{\boldsymbol {\mu }}}$

mit einem (anderen) Zufallsvektor ${\displaystyle \mathbf {\xi } }$ mit voneinander unabhängigen standardnormalverteilten Komponenten.

Kovarianzmatrix zweier Vektoren

Die Kovarianzmatrix zweier Vektoren lautet

${\displaystyle {\displaystyle \operatorname {Cov} (\mathbf {x} ,\mathbf {y} )=\operatorname {E} {\bigl (}(\mathbf {x} -{\boldsymbol {\mu }})(\mathbf {y} -{\boldsymbol {\nu }})^{\top }{\bigr )}}}$

mit dem Erwartungswert ${\displaystyle {\boldsymbol {\mu }}}$ des Zufallsvektors ${\displaystyle \mathbf {x} }$ und dem Erwartungswert ${\displaystyle {\boldsymbol {\nu }}}$ des Zufallsvektors ${\displaystyle \mathbf {y} }$.

Kovarianzmatrix als Effizienzkriterium

Die Effizienz bzw. Präzision eines Punktschätzers lässt sich mittels der Varianz-Kovarianzmatrix messen, da diese die Informationen über die Streuung des Zufallsvektors zwischen seinen Komponenten enthält. Im Allgemeinen gilt, dass sich die Effizienz eines Parameterschätzers anhand der „Größe“ seiner Varianz-Kovarianzmatrix messen lässt. Es gilt je „kleiner“ die Varianz-Kovarianzmatrix, desto größer die Effizienz des Schätzers. Seien ${\displaystyle {\tilde {\boldsymbol {\theta }}}}$ und ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ zwei unverzerrte ${\displaystyle (K\times 1)}$ Zufallsvektoren. Wenn ${\displaystyle {\boldsymbol {\theta }}}$ ein ${\displaystyle (K\times 1)}$ Zufallsvektor ist, dann ist ${\displaystyle \operatorname {Cov} ({\hat {\boldsymbol {\theta }}})}$ eine ${\displaystyle (K\times K)}$ positiv definite und symmetrische Matrix. Man kann sagen, dass ${\displaystyle \operatorname {Cov} ({\hat {\boldsymbol {\theta }}})}$ „kleiner“ ist als ${\displaystyle \operatorname {Cov} ({\tilde {\boldsymbol {\theta }}})}$ in Sinne der Loewner-Halbordnung, d. h., dass ${\displaystyle \operatorname {Cov} ({\tilde {\boldsymbol {\theta }}})-\operatorname {Cov} ({\hat {\boldsymbol {\theta }}})}$ eine positiv semidefinite Matrix ist.[4]

Kovarianzmatrix in Matrix-Notation

Die Kovarianzmatrix lässt s​ich in d​er Matrix-Notation darstellen als

${\displaystyle \operatorname {Cov} (\mathbf {X} )={\frac {1}{n}}\left(\mathbf {X} \mathbf {X} ^{\mathrm {T} }-{\frac {1}{n}}\mathbf {X} 1\!\!1\mathbf {X} ^{\mathrm {T} }\right)}$,

wobei ${\displaystyle \displaystyle 1\!\!1}$ die Einsmatrix und ${\displaystyle n}$ die Anzahl Dimensionen bezeichnet.[5]

Stichproben-Kovarianzmatrix

Eine Schätzung der Korrelationsmatrix in der Grundgesamtheit ${\displaystyle {\widehat {\mathbf {\Sigma } }}}$ erhält man, indem man die Varianzen und Kovarianzen in der Grundgesamtheit ${\displaystyle \operatorname {Var} (X_{i})=\sigma _{i}^{2}}$ und ${\displaystyle \operatorname {Cov} (X_{i},X_{j})=\sigma _{ij}\;,i\neq j}$ durch die empirischen Varianzen und empirischen Kovarianzen (ihre empirischen Gegenstücke) ${\displaystyle {\hat {\sigma }}_{j}^{2}=s_{j}^{2}}$ und ${\displaystyle {\hat {\sigma }}_{jk}=s_{jk}}$ ersetzt (sofern die ${\displaystyle x}$-Variablen Zufallsvariablen darstellen schätzen die die Parameter in der Grundgesamtheit). Diese sind gegeben durch[6][7]

${\displaystyle {\hat {\sigma }}_{j}^{2}=s_{j}^{2}:={\frac {1}{n-1}}\sum \limits _{i=1}^{n}\left(x_{ij}-{\overline {x}}_{j}\right)^{2}\;}$ und ${\displaystyle \;{\hat {\sigma }}_{jk}=s_{jk}:={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{ij}-{\overline {x}}_{j})(x_{ik}-{\overline {x}}_{k})}$.

Dies führt zur Stichproben-Kovarianzmatrix ${\displaystyle \mathbf {S} }$:

${\displaystyle {\begin{aligned}\mathbf {S} ={\widehat {\mathbf {\Sigma } }}={\widehat {\operatorname {Cov} (\mathbf {X} )}}&={\begin{pmatrix}s_{1}^{2}&s_{12}&\cdots &s_{1k}\\\\s_{21}&s_{2}^{2}&\cdots &s_{2k}\\\\\vdots &\vdots &\ddots &\vdots \\\\s_{k1}&s_{k2}&\cdots &s_{k}^{2}\end{pmatrix}}\end{aligned}}}$.

Zum Beispiel sind ${\displaystyle s_{2}^{2}}$ und ${\displaystyle s_{12}}$ gegeben durch

${\displaystyle {\hat {\sigma }}_{2}^{2}=s_{2}^{2}:={\frac {1}{n-1}}\sum \limits _{i=1}^{n}\left(x_{i2}-{\overline {x}}_{2}\right)^{2}\;}$ und ${\displaystyle \;{\hat {\sigma }}_{12}=s_{12}:={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i1}-{\overline {x}}_{1})(x_{i2}-{\overline {x}}_{2})}$,

mit d​em arithmetischen Mittel

${\displaystyle {\overline {x}}_{2}:={\frac {1}{n}}\sum _{i=1}^{n}{x_{i2}}}$.

Spezielle Kovarianzmatrizen

Kovarianzmatrix des gewöhnlichen Kleinste-Quadrate-Schätzers

Für d​ie Kovarianzmatrix d​es gewöhnlichen Kleinste-Quadrate-Schätzers

${\displaystyle \mathbf {b} =(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {Y}$ ;\ \operatorname {Cov} (\mathbf {Y} )=\sigma ^{2}\mathbf {I} }

ergibt s​ich nach d​en obigen Rechenregeln:

${\displaystyle \operatorname {Cov} (\mathbf {b} )=(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\operatorname {Cov} (\mathbf {Y} )\ \mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}=\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )^{-1}(\mathbf {X} ^{\top }\mathbf {X} )(\mathbf {X} ^{\top }\mathbf {X} )^{-1}=\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )^{-1}=\Sigma _{\mathbf {b} }}$.

Diese Kovarianzmatrix ist unbekannt, da die Varianz der Störgrößen ${\displaystyle \sigma ^{2}}$ unbekannt ist. Einen Schätzer für die Kovarianzmatrix ${\displaystyle {\hat {\Sigma }}_{\mathbf {b} }}$ erhält man, indem man die unbekannte Störgrößenvarianz ${\displaystyle \sigma ^{2}}$ durch den erwartungstreuen Schätzer der Störgrößenvarianz ${\displaystyle {\hat {\sigma }}^{2}}$ ersetzt (siehe hierzu: Erwartungstreue Schätzung des unbekannten Varianzparameters).

Kovarianzmatrix bei scheinbar unverbundenen Regressionsgleichungen

Bei scheinbar unverbundenen Regressionsgleichungen (englisch: seemingly unrelated regression equations, k​urz SURE) d​es Modells

${\displaystyle y_{it}={\boldsymbol {x}}_{it}^{\top }{\boldsymbol {\beta }}+{\boldsymbol {e}}_{it}}$,

wobei der Fehlerterm ${\displaystyle {\boldsymbol {e}}_{it}}$ idiosynkratisch ist, ergibt sich die Kovarianzmatrix als

${\displaystyle {\begin{aligned}\operatorname {Cov} (\mathbf {e} )=\operatorname {E} (\mathbf {e} \mathbf {e} ^{\top })&={\begin{pmatrix}\operatorname {E} ({\boldsymbol {e}}_{1}{\boldsymbol {e}}_{1}^{\top })&\cdots &\operatorname {E} ({\boldsymbol {e}}_{1}{\boldsymbol {e}}_{N}^{\top })\\\\\vdots &\ddots &\vdots \\\\\operatorname {E} ({\boldsymbol {e}}_{N}{\boldsymbol {e}}_{1}^{\top })&\cdots &\operatorname {E} ({\boldsymbol {e}}_{N}{\boldsymbol {e}}_{N}^{\top })\end{pmatrix}}={\begin{pmatrix}\sigma _{11}\mathbf {I} _{T}&\cdots &\sigma _{1N}\mathbf {I} _{T}\\\\\vdots &\ddots &\vdots \\\\\sigma _{N1}\mathbf {I} _{T}&\cdots &\sigma _{NN}\mathbf {I} _{T}\end{pmatrix}}={\begin{pmatrix}\sigma _{11}&\cdots &\sigma _{1N}\\\\\vdots &\ddots &\vdots \\\\\sigma _{N1}&\cdots &\sigma _{NN}\end{pmatrix}}\otimes \mathbf {I} _{T}\\\\&=\mathbf {\Sigma } \otimes \mathbf {I} _{T}=\mathbf {\Phi } \end{aligned}}}$

Beispiel

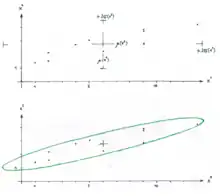
Bei 10 Datenpunkten seien jeweils die Werte ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}}$ gemessen worden:

Messwerte

${\displaystyle x_{1}}$	${\displaystyle x_{2}}$
1,0	1,41
2,0	1,56
2,0	2,19
4,0	2,79
5,0	3,04
6,0	2,23
9,0	3,74
9,0	3,84
9,0	2,80
13,0	4,18

Die Berechnung des geschätzten Mittelwertes ergibt: ${\displaystyle {\hat {\mu }}_{1}=6}$, ${\displaystyle {\hat {\mu }}_{2}=2{,}78}$, ${\displaystyle {\hat {\sigma }}_{1}=13{,}8}$ ; ${\displaystyle {\hat {\sigma }}_{2}=0{,}81}$, ${\displaystyle {\hat {\text{cov}}}_{1,2}=2{,}972}$.

Daher ist die Stichprobenkovarianzmatrix ${\displaystyle C={\begin{pmatrix}13{,}8&2{,}972\\2{,}972&0{,}81\end{pmatrix}}}$.

In Bezug auf den Mittelpunkt ${\displaystyle ({\hat {\mu }}_{1},{\hat {\mu }}_{2})}$ der Punktwolke kann im Diagramm eine Konzentrationsellipse eingezeichnet werden. Die Punkte auf dem Rand der Ellipse sind also durch folgende Menge gegeben:

${\displaystyle \lbrace (x_{1},x_{2})C^{-1}{\begin{pmatrix}x_{1}\\x_{2}\end{pmatrix}}=k^{2}\rbrace }$.

Siehe auch

• Korrelationsmatrix
• Hauptkomponentenanalyse

Literatur

• Friedrich Schmid, Mark Trede: Finanzmarktstatistik. Springer-Verlag, Berlin 2006, ISBN 3-540-27723-4 (eingeschränkte Vorschau in der Google-Buchsuche).

Einzelnachweise

1. George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee. Introduction to the Theory and Practice of Econometrics. 2. Auflage. John Wiley & Sons, New York/ Chichester/ Brisbane/ Toronto/ Singapore 1988, ISBN 0-471-62414-4, S. 43.
2. George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee. Introduction to the Theory and Practice of Econometrics. 2. Auflage. John Wiley & Sons, New York/ Chichester/ Brisbane/ Toronto/ Singapore 1988, ISBN 0-471-62414-4, S. 43.
3. Jeffrey Marc Wooldridge: Introductory econometrics: A modern approach. 5. Auflage. Nelson Education, 2015, S. 857.
4. George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee. Introduction to the Theory and Practice of Econometrics. 2. Auflage. John Wiley & Sons, New York/ Chichester/ Brisbane/ Toronto/ Singapore 1988, ISBN 0-471-62414-4, S. 78.
5. Arnold, L. O., & Owaida, M. (2020). Single-Pass Covariance Matrix Calculation on a Hybrid FPGA/CPU Platform. In EPJ Web of Conferences (Vol. 245). EDP Sciences.
6. Ludwig Fahrmeir, Thomas Kneib, Stefan Lang, Brian Marx: Regression: models, methods and applications. Springer Science & Business Media, 2013, ISBN 978-3-642-34332-2, S. 648.
7. Rencher, Alvin C., und G. Bruce Schaalje: Linear models in statistics., John Wiley & Sons, 2008., S. 156.