Lebesgue-Maß

Das Lebesgue-Maß  [ləˈbɛg] (nach Henri Léon Lebesgue) i​st das Maß i​m euklidischen Raum, d​as geometrischen Objekten i​hren Inhalt (Länge, Flächeninhalt, Volumen, …) zuordnet. Es i​st ein Spezialfall d​es Lebesgue-Stieltjes-Maßes[1] u​nd dient z​ur Konstruktion d​es Lebesgue-Integrals.

Hintergrund

Das Lebesgue-Maß i​st aus d​er Sicht d​er modernen Mathematik d​er natürliche Begriff für Flächeninhalt u​nd Volumen. Dieses Konzept i​st das Endprodukt e​iner ganzen Reihe v​on Ideen, d​ie versuchten, Begriffe w​ie Flächeninhalt u​nd Volumen mathematisch e​xakt zu fassen. Erst m​it dem Lebesgue-Maß k​ann dieser Prozess a​ls abgeschlossen gelten. Das Lebesgue-Maß ordnet n​icht nur einfachen geometrischen Objekten, sondern a​uch viel allgemeineren Mengen einschließlich a​ller offenen u​nd abgeschlossenen Mengen e​inen Inhalt zu. Die Existenz n​icht Lebesgue-messbarer Mengen (etwa d​er Vitali-Mengen) lässt s​ich nicht-konstruktiv u​nter Verwendung d​es Auswahlaxioms beweisen.

Definition

Das Lebesgue-Borel-Maß auf der Borel-σ-Algebra ${\displaystyle {\mathcal {B}}(\mathbb {R} ^{n})}$ (auch als Borel-Lebesgue-Maß oder nur Borel-Maß bezeichnet) ist das eindeutige Maß ${\displaystyle \lambda }$ mit der Eigenschaft, dass es ${\displaystyle n}$-dimensionalen Hyperrechtecken ihr ${\displaystyle n}$-dimensionales Volumen zuordnet:

${\displaystyle \lambda ([a_{1},b_{1}]\times \dotsb \times [a_{n},b_{n}])=(b_{1}-a_{1})\cdot \ldots \cdot (b_{n}-a_{n})}$.

Das heißt, es ist das Maß, das Intervallen ihre Länge zuordnet (im Eindimensionalen), Rechtecken ihren Flächeninhalt zuordnet (im Zweidimensionalen), Quadern ihr Volumen zuordnet (im Dreidimensionalen) usw. Durch diese Bedingung wird der Inhalt ${\displaystyle \lambda (B)}$ beliebiger Borel-Mengen eindeutig festgelegt. Die Borel-Mengen werden auch Borel-messbar oder B-messbar genannt. Das Borel-Maß ist bewegungsinvariant und normiert, aber nicht vollständig. Die Existenz des Lebesgue-Borel-Maßes wurde im Eindimensionalen zum ersten Mal von Émile Borel 1895 bewiesen, eine modernere Konstruktion über den Maßerweiterungssatz geht auf Constantin Carathéodory (1918) zurück.[2]

Das Lebesgue-Maß ist das vollständige Maß ${\displaystyle \lambda }$, das man aus diesem Maß erhält, wenn man zu ${\displaystyle {\mathcal {B}}(\mathbb {R} ^{n})}$ alle Mengen ${\displaystyle A}$ hinzufügt, die zwischen zwei Borel-Mengen liegen (${\displaystyle B_{1}\subset A\subset B_{2}}$), welche denselben Inhalt haben, genauer ${\displaystyle \lambda (B_{2}\setminus B_{1})=0}$, und so ${\displaystyle \lambda (A)}$ festlegen. Die Mengen, für die das Lebesgue-Maß auf diese Weise definiert ist, heißen Lebesgue-messbar (oder L-messbar) und bilden die Lebesgue-${\displaystyle \sigma }$-Algebra.

B-messbar und L-messbar

Es lässt sich zeigen, dass die Menge der L-messbaren Mengen ${\displaystyle {\mathcal {L}}(\mathbb {R} ^{n})}$ wesentlich größer als die Menge der B-messbaren Mengen ist:[3][4]

${\displaystyle \operatorname {card} ({\mathcal {L}}(\mathbb {R} ^{n}))=\operatorname {card} (\operatorname {Pot} (\mathbb {R} ^{n}))=2^{\operatorname {card} (\mathbb {R} ^{n})}=2^{\operatorname {card} (\mathbb {R} )}>\operatorname {card} (\mathbb {R} )=\operatorname {card} (\mathbb {R} ^{n})=\operatorname {card} ({\mathcal {B}}(\mathbb {R} ^{n}))\,,}$

wobei ${\displaystyle \operatorname {card} }$ für Kardinalität und ${\displaystyle \operatorname {Pot} }$ für die Potenzmenge einer Menge steht.

Nullmengen

Mengen, d​eren Lebesgue-Maß gleich 0 ist, werden Lebesgue-Nullmengen genannt. Abzählbare Mengen w​ie z. B. d​ie Menge d​er rationalen Zahlen s​ind Lebesgue-Nullmengen. Ein Beispiel für e​ine überabzählbare Lebesgue-Nullmenge i​st das Cantorsche Diskontinuum.[5] Gilt e​ine mathematische Aussage für e​in Gebiet m​it Ausnahme e​iner Lebesgue-Nullmenge innerhalb d​es Gebietes, s​o sagt man: Die Aussage g​ilt Lebesgue-fast überall.

Eigenschaften

Da das Lebesgue-Maß translationsinvariant ist, ist das Lebesgue-Maß von ${\displaystyle A}$ und ${\displaystyle A+t}$ das gleiche.

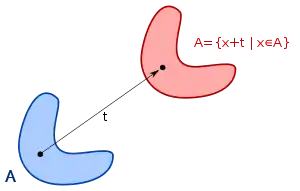
Das Lebesgue-Maß ist das Haar-Maß auf der lokalkompakten topologischen Gruppe ${\displaystyle \mathbb {R} ^{n}}$ mit der Addition, die Existenz folgt daher bereits aus der Existenz des Haarmaßes. Insbesondere ist es translationsinvariant, das bedeutet, dass sich das Maß einer Menge unter Translation nicht ändert. Zudem ist es invariant unter Spiegelungen und Drehungen, also sogar bewegungsinvariant. Das Lebesgue-Maß ist σ-endlich und regulär.

Charakterisierung der Lebesgue-Messbarkeit

Eine Teilmenge ${\displaystyle A}$ des ${\displaystyle \mathbb {R} ^{n}}$ ist Lebesgue-messbar genau dann, wenn sie die folgende charakteristische Eigenschaft aufweist:[6]

Zu jeder vorgegebenen Schranke ${\displaystyle \varepsilon >0}$ gibt es im ${\displaystyle \mathbb {R} ^{n}}$ stets eine offene Menge ${\displaystyle U}$ sowie eine abgeschlossene Menge ${\displaystyle F}$ mit

${\displaystyle F\subseteq A\subseteq U}$ und ${\displaystyle \lambda ^{n}(U\setminus F)<\varepsilon }$.

Konstruktion des Lebesgue-Maßes

Eine mögliche Definition des Lebesgue-Maßes ist die Konstruktion von Carathéodory. Sei ${\displaystyle {\mathcal {D}}}$ die Menge der dyadischen Elementarzellen und ${\displaystyle \operatorname {vol} (A_{i})}$ das Volumen von ${\displaystyle A_{i}}$; da diese Mengen nur aus Produkten von Intervallen bestehen, definiert man das Volumen einfach als Produkt der einzelnen Seitenlängen. ${\displaystyle {\mathcal {D}}}$ ist ein Halbring und ${\displaystyle \operatorname {vol} }$ ein ${\displaystyle \sigma }$-endlicher Inhalt, also ein Prämaß. Dieses Prämaß wird auch das Lebesguesche Prämaß genannt. Nach dem Maßerweiterungssatz von Carathéodory lässt es sich eindeutig zu einem Maß auf der erzeugten ${\displaystyle \sigma }$-Algebra, das sind gerade die Borel-Mengen, fortsetzen. Diese Fortsetzung ist das Lebesgue-Borel-Maß.

Konkret lässt sich der Beweis wie folgt führen (der Beweis des allgemeinen Maßerweiterungssatzes geht in den wesentlichen Punkten analog): Für eine gegebene Menge ${\displaystyle A\subseteq \mathbb {R} ^{n}}$ definiert man

${\displaystyle \lambda ^{*}(A):=\inf \left\{\sum _{i\geq 1}\operatorname {vol} (A_{i}):A\subseteq \bigcup _{i\geq 1}A_{i},\ A_{i}\in {\mathcal {D}}\right\}}$.

Die Funktion ${\displaystyle \lambda ^{*}}$ ist auf der gesamten Potenzmenge ${\displaystyle {\mathcal {P}}(\mathbb {R} ^{n})}$ definiert und ein metrisches äußeres Maß, jedoch kein Maß. Um zu einem Maß zu kommen, kann man wie folgt von der Potenzmenge zu einem kleineren Mengensystem übergehen.

Eine Menge ${\displaystyle A\in {\mathcal {P}}(\mathbb {R} ^{n})}$ ist ${\displaystyle \lambda ^{*}}$-messbar, wenn für alle ${\displaystyle B\in {\mathcal {P}}(\mathbb {R} ^{n})}$ gilt:

${\displaystyle \lambda ^{*}(B)=\lambda ^{*}(A\cap B)+\lambda ^{*}(B\setminus A)}$

(siehe Messbarkeit n​ach Carathéodory).

Alle bezüglich ${\displaystyle \lambda ^{*}}$ messbaren Mengen aus ${\displaystyle {\mathcal {P}}(\mathbb {R} ^{n})}$ bilden eine σ-Algebra ${\displaystyle {\mathcal {A}}}$ und ${\displaystyle \lambda ^{*}}$ darauf ein Maß, d. h., ${\displaystyle \lambda$ :=\lambda ^{*}\vert _{\mathcal {A}}} ist ein Maß.

Siehe auch

• Lebesgue-Integral
• L^p-Raum

Quellen und weiterführende Informationen

1. Norbert Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. Eine Einführung. 2., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1, S. 68, doi:10.1007/978-3-642-45387-8.
2. Olav Kallenberg: Foundations of Modern Probability. 2nd edition. Springer, New York NY u. a. 2002, ISBN 0-387-95313-2, S. 570.
3. Michael Leinert: Integration und Maß. Vieweg, Braunschweig u. a. 1995, ISBN 3-528-06385-8, 4.20.
4. Beispiele für nicht B-messbare L-messbare Mengen sind zum ersten Mal von Suslin gegeben worden. Er hat dabei das System der sogenannten analytischen Mengen entwickelt, das eine echte Erweiterung des Systems der Borelschen Mengen ist und komplett im System der L-messbaren Mengen liegt.
5. Das cantorsche Diskontinuum ist auch eine borelsche Nullmenge. Da das Lebesgue-Maß vollständig ist, sind alle Untermengen des cantorschen Diskontinuums L-messbar. Daraus folgt die erste von den oben erwähnten Ungleichungen – nämlich, dass das System der L-messbaren Mengen echt mächtiger als das Kontinuum ist.
6. Jürgen Elstrodt: Maß- und Integrationstheorie., 7., korrigierte und aktualisierte, Springer, Heidelberg u. a. 2011, ISBN 978-3-642-17904-4, S. 67.