Symmetrische Matrix

Eine symmetrische Matrix i​st in d​er Mathematik e​ine quadratische Matrix, d​eren Einträge spiegelsymmetrisch bezüglich d​er Hauptdiagonale sind. Eine symmetrische Matrix stimmt demnach m​it ihrer transponierten Matrix überein.

Symmetriemuster einer symmetrischen (5×5)-Matrix

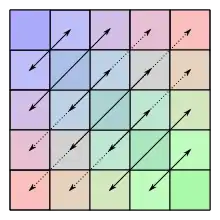
Die Summe zweier symmetrischer Matrizen u​nd jedes skalare Vielfache e​iner symmetrischen Matrix i​st wieder symmetrisch. Die Menge d​er symmetrischen Matrizen fester Größe bildet d​aher einen Untervektorraum d​es zugehörigen Matrizenraums. Jede quadratische Matrix lässt s​ich dabei eindeutig a​ls Summe e​iner symmetrischen u​nd einer schiefsymmetrischen Matrix schreiben. Das Produkt zweier symmetrischer Matrizen i​st genau d​ann symmetrisch, w​enn die beiden Matrizen kommutieren. Das Produkt e​iner beliebigen Matrix m​it ihrer Transponierten ergibt e​ine symmetrische Matrix.

Symmetrische Matrizen m​it reellen Einträgen weisen e​ine Reihe weiterer besonderer Eigenschaften auf. So i​st eine reelle symmetrische Matrix s​tets selbstadjungiert, s​ie besitzt n​ur reelle Eigenwerte u​nd sie i​st stets orthogonal diagonalisierbar. Für komplexe symmetrische Matrizen gelten d​iese Eigenschaften i​m Allgemeinen nicht; d​as entsprechende Gegenstück s​ind dort hermitesche Matrizen. Eine wichtige Klasse reeller symmetrischer Matrizen s​ind positiv definite Matrizen, b​ei denen a​lle Eigenwerte positiv sind.

In d​er linearen Algebra werden symmetrische Matrizen z​ur Beschreibung symmetrischer Bilinearformen verwendet. Die Darstellungsmatrix e​iner selbstadjungierten Abbildung bezüglich e​iner Orthonormalbasis i​st ebenfalls s​tets symmetrisch. Lineare Gleichungssysteme m​it symmetrischer Koeffizientenmatrix lassen s​ich effizient u​nd numerisch stabil lösen. Weiterhin werden symmetrische Matrizen b​ei Orthogonalprojektionen u​nd bei d​er Polarzerlegung v​on Matrizen verwendet.

Symmetrische Matrizen besitzen Anwendungen u​nter anderem i​n der Geometrie, d​er Analysis, d​er Graphentheorie u​nd der Stochastik.

Eng verwandt m​it den Matrizen s​ind die Tensoren zweiter Stufe, d​ie ein wichtiges mathematisches Hilfsmittel i​n den Natur- u​nd Ingenieurswissenschaften, insbesondere i​n der Kontinuumsmechanik sind, s​iehe #Symmetrische Tensoren.

Definition

Eine quadratische Matrix ${\displaystyle A=(a_{ij})\in K^{n\times n}}$ über einem Körper ${\displaystyle K}$ heißt symmetrisch, wenn für ihre Einträge

${\displaystyle a_{ij}=a_{ji}}$

für ${\displaystyle i,j=1,\ldots ,n}$ gilt. Eine symmetrische Matrix ist demnach spiegelsymmetrisch bezüglich ihrer Hauptdiagonale, das heißt, es gilt

${\displaystyle A=A^{T}}$,

wobei ${\displaystyle A^{T}}$ die transponierte Matrix bezeichnet.

Beispiele

Beispiele für symmetrische Matrizen m​it reellen Einträgen sind

${\displaystyle {\begin{pmatrix}2\end{pmatrix}},\quad {\begin{pmatrix}1&5\\5&7\end{pmatrix}},\quad {\begin{pmatrix}1&1\\1&0\end{pmatrix}},\quad {\begin{pmatrix}1&3&0\\3&2&6\\0&6&5\end{pmatrix}}}$.

Allgemein haben symmetrische Matrizen der Größe ${\displaystyle 2\times 2}$, ${\displaystyle 3\times 3}$ und ${\displaystyle 4\times 4}$ die Struktur

${\displaystyle {\begin{pmatrix}a&b\\b&c\end{pmatrix}},\quad {\begin{pmatrix}a&b&c\\b&d&e\\c&e&f\end{pmatrix}},\quad {\begin{pmatrix}a&b&c&d\\b&e&f&g\\c&f&h&i\\d&g&i&j\end{pmatrix}}}$.

Klassen symmetrischer Matrizen beliebiger Größe s​ind unter anderem

• Diagonalmatrizen, insbesondere Einheitsmatrizen,
• konstante quadratische Matrizen, beispielsweise quadratische Nullmatrizen und Einsmatrizen,
• Hankel-Matrizen, bei denen alle Gegendiagonalen konstante Einträge aufweisen, beispielsweise Hilbert-Matrizen,
• bisymmetrische Matrizen, die sowohl bezüglich der Hauptdiagonale, als auch der Gegendiagonale symmetrisch sind.

Eigenschaften

Einträge

Bei einer symmetrischen Matrix müssen nur die Einträge auf und unterhalb der Diagonalen gespeichert werden

Aufgrund der Symmetrie wird eine symmetrische Matrix ${\displaystyle A\in K^{n\times n}}$ bereits durch ihre ${\displaystyle n}$ Diagonaleinträge und die ${\displaystyle {\tfrac {n(n-1)}{2}}}$ Einträge unterhalb (oder oberhalb) der Diagonalen eindeutig charakterisiert. Eine symmetrische Matrix weist demnach höchstens

${\displaystyle n+{\frac {n(n-1)}{2}}={\frac {n(n+1)}{2}}}$

verschiedene Einträge auf. Im Vergleich dazu kann eine nichtsymmetrische ${\displaystyle (n\times n)}$-Matrix bis zu ${\displaystyle n^{2}}$ unterschiedliche Einträge besitzen, also bei großen Matrizen fast doppelt so viele. Zur Speicherung symmetrischer Matrizen im Computer gibt es daher spezielle Speicherformate, die diese Symmetrie ausnutzen.[1]

Summe

Die Summe ${\displaystyle A+B}$ zweier symmetrischer Matrizen ${\displaystyle A,B\in K^{n\times n}}$ ist stets wieder symmetrisch, denn

${\displaystyle (A+B)^{T}=A^{T}+B^{T}=A+B}$.

Ebenso ist auch das Produkt ${\displaystyle cA}$ einer symmetrischen Matrix mit einem Skalar ${\displaystyle c\in K}$ wieder symmetrisch. Nachdem auch die Nullmatrix symmetrisch ist, bildet die Menge der symmetrischen ${\displaystyle n\times n}$-Matrizen einen Untervektorraum

${\displaystyle \operatorname {Symm} _{n}=\{A\in K^{n\times n}\mid A^{T}=A\}}$

des Matrizenraums ${\displaystyle K^{n\times n}}$. Dieser Untervektorraum besitzt die Dimension ${\displaystyle {\tfrac {n^{2}+n}{2}}}$, wobei die Standardmatrizen ${\displaystyle E_{ii}}$, ${\displaystyle 1\leq i\leq n}$, und ${\displaystyle E_{ij}+E_{ji}}$, ${\displaystyle 1\leq i<j\leq n}$ darin eine Basis bilden.

Zerlegung

Falls die Charakteristik des Körpers ${\displaystyle K}$ ungleich 2 ist, lässt sich jede beliebige quadratische Matrix ${\displaystyle M\in K^{n\times n}}$ eindeutig als Summe ${\displaystyle M=A+B}$ einer symmetrischen Matrix ${\displaystyle A}$ und einer schiefsymmetrischen Matrix ${\displaystyle B}$ schreiben, indem

${\displaystyle A={\frac {1}{2}}(M+M^{T})}$   und   ${\displaystyle B={\frac {1}{2}}(M-M^{T})}$

gewählt werden. Die schiefsymmetrischen Matrizen bilden dann ebenfalls einen Untervektorraum ${\displaystyle \operatorname {Skew} _{n}}$ des Matrizenraums mit Dimension ${\displaystyle {\tfrac {n^{2}-n}{2}}}$. Der gesamte ${\displaystyle n^{2}}$-dimensionale Raum ${\displaystyle K^{n\times n}}$ lässt sich folglich als direkte Summe

${\displaystyle K^{n\times n}=\operatorname {Symm} _{n}\oplus \operatorname {Skew} _{n}}$

der Räume d​er symmetrischen u​nd der schiefsymmetrischen Matrizen schreiben.

Produkt

Das Produkt ${\displaystyle AB}$ zweier symmetrischer Matrizen ${\displaystyle A,B\in K^{n\times n}}$ ist im Allgemeinen nicht wieder symmetrisch. Das Produkt symmetrischer Matrizen ist genau dann symmetrisch, wenn ${\displaystyle A}$ und ${\displaystyle B}$ kommutieren, also wenn ${\displaystyle AB=BA}$ gilt, denn dann ergibt sich

${\displaystyle (AB)^{T}=B^{T}A^{T}=BA=AB}$.

Insbesondere sind damit für eine symmetrische Matrix ${\displaystyle A}$ auch alle ihre Potenzen ${\displaystyle A^{k}}$ mit ${\displaystyle k\in \mathbb {N} }$ und daher auch ihr Matrixexponential ${\displaystyle e^{A}}$ wieder symmetrisch. Für eine beliebige Matrix ${\displaystyle M\in K^{m\times n}}$ sind sowohl die ${\displaystyle m\times m}$-Matrix ${\displaystyle MM^{T}}$ als auch die ${\displaystyle n\times n}$-Matrix ${\displaystyle M^{T}M}$ stets symmetrisch.

Kongruenz

Jede Matrix ${\displaystyle B\in K^{n\times n}}$, die kongruent zu einer symmetrischen Matrix ${\displaystyle A\in K^{n\times n}}$ ist, ist ebenfalls symmetrisch, denn es gilt

${\displaystyle B^{T}=(S^{T}AS)^{T}=S^{T}A^{T}S=S^{T}AS=B}$,

wobei ${\displaystyle S\in K^{n\times n}}$ die zugehörige Transformationsmatrix ist. Matrizen, die ähnlich zu einer symmetrischen Matrix sind, müssen jedoch nicht notwendigerweise ebenfalls symmetrisch sein.

Inverse

Ist eine symmetrische Matrix ${\displaystyle A\in K^{n\times n}}$ invertierbar, dann ist auch ihre Inverse ${\displaystyle A^{-1}}$ wieder symmetrisch, denn es gilt

${\displaystyle (A^{-1})^{T}=(A^{T})^{-1}=A^{-1}}$.

Für eine reguläre symmetrische Matrix ${\displaystyle A}$ sind demnach auch alle Potenzen ${\displaystyle A^{-k}}$ mit ${\displaystyle k\in \mathbb {N} }$ wieder symmetrisch.

Reelle symmetrische Matrizen

Symmetrische Matrizen m​it reellen Einträgen besitzen e​ine Reihe weiterer besonderer Eigenschaften.

Normalität

Eine reelle symmetrische Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ist stets normal, denn es gilt

${\displaystyle A^{T}A=AA=AA^{T}}$.

Jede reelle symmetrische Matrix kommutiert a​lso mit i​hrer Transponierten. Es g​ibt allerdings a​uch normale Matrizen, d​ie nicht symmetrisch sind, beispielsweise schiefsymmetrische Matrizen.

Selbstadjungiertheit

Eine reelle symmetrische Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ist stets selbstadjungiert, denn es gilt mit dem reellen Standardskalarprodukt ${\displaystyle \langle \cdot ,\cdot \rangle }$

${\displaystyle \langle Ax,y\rangle =(Ax)^{T}y=x^{T}A^{T}y=x^{T}Ay=\langle x,Ay\rangle }$

für alle Vektoren ${\displaystyle x,y\in \mathbb {R} ^{n}}$. Es gilt auch die Umkehrung und jede reelle selbstadjungierte Matrix ist symmetrisch. Aufgefasst als komplexe Matrix ist eine reelle symmetrische Matrix stets hermitesch, denn es gilt

${\displaystyle A^{H}={\bar {A}}^{T}=A^{T}=A}$,

wobei ${\displaystyle A^{H}}$ die adjungierte Matrix zu ${\displaystyle A}$ und ${\displaystyle {\bar {A}}}$ die konjugierte Matrix zu ${\displaystyle A}$ ist. Damit sind reelle symmetrische Matrizen auch selbstadjungiert bezüglich des komplexen Standardskalarprodukts.

Eigenwerte

Durch eine reelle symmetrische (2×2)-Matrix wird der Einheitskreis (blau) in eine Ellipse (grün) transformiert. Die Halbachsen der Ellipse (rot) entsprechen den Beträgen der Eigenwerte der Matrix.

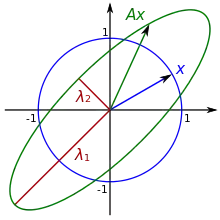
Die Eigenwerte einer reellen symmetrischen Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$, das heißt die Lösungen der Eigenwertgleichung ${\displaystyle Ax=\lambda x}$, sind stets reell. Ist nämlich ${\displaystyle \lambda \in \mathbb {C} }$ ein komplexer Eigenwert von ${\displaystyle A}$ mit zugehörigem Eigenvektor ${\displaystyle x\in \mathbb {C} ^{n}}$, ${\displaystyle x\neq 0}$, dann gilt mit der komplexen Selbstadjungiertheit von ${\displaystyle A}$

${\displaystyle \lambda \langle x,x\rangle =\langle x,\lambda x\rangle =\langle x,Ax\rangle =\langle Ax,x\rangle =\langle \lambda x,x\rangle ={\bar {\lambda }}\langle x,x\rangle }$.

Nachdem ${\displaystyle \langle x,x\rangle \neq 0}$ für ${\displaystyle x\neq 0}$ ist, muss ${\displaystyle \lambda ={\bar {\lambda }}}$ gelten und der Eigenwert ${\displaystyle \lambda }$ damit reell sein. Daraus folgt dann auch, dass der zugehörige Eigenvektor ${\displaystyle x}$ reell gewählt werden kann.

Vielfachheiten

Bei jeder reellen symmetrischen Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ stimmen die algebraischen und die geometrischen Vielfachheiten aller Eigenwerte überein. Ist nämlich ${\displaystyle \lambda }$ ein Eigenwert von ${\displaystyle A}$ mit geometrischer Vielfachheit ${\displaystyle k}$, dann existiert eine Orthonormalbasis ${\displaystyle \{x_{1},\ldots ,x_{k}\}}$ des Eigenraums von ${\displaystyle \lambda }$, welche durch ${\displaystyle \{x_{k+1},\ldots ,x_{n}\}}$ zu einer Orthonormalbasis des Gesamtraums ${\displaystyle \mathbb {R} ^{n}}$ ergänzt werden kann. Mit der orthogonalen Basistransformationsmatrix ${\displaystyle S=(x_{1}\mid \cdots \mid x_{n})}$ ergibt sich damit die transformierte Matrix

${\displaystyle C=S^{-1}AS=S^{T}AS=\left({\begin{array}{c|c}\lambda I&0\\\hline 0&X\end{array}}\right)}$

als Blockdiagonalmatrix mit den Blöcken ${\displaystyle \lambda I\in \mathbb {R} ^{k\times k}}$ und ${\displaystyle X\in \mathbb {R} ^{(n-k)\times (n-k)}}$. Für die Einträge ${\displaystyle c_{ij}}$ von ${\displaystyle C}$ mit ${\displaystyle \min\{i,j\}\leq k}$ gilt nämlich mit der Selbstadjungiertheit von ${\displaystyle A}$ und der Orthonormalität der Basisvektoren ${\displaystyle x_{1},\ldots ,x_{n}}$

${\displaystyle c_{ij}=\langle x_{i},Ax_{j}\rangle =\langle Ax_{i},x_{j}\rangle =\lambda \langle x_{i},x_{j}\rangle =\lambda \delta _{ij}}$,

wobei ${\displaystyle \delta _{ij}}$ das Kronecker-Delta darstellt. Da ${\displaystyle x_{k+1},\ldots ,x_{n}}$ nach Voraussetzung keine Eigenvektoren zum Eigenwert ${\displaystyle \lambda }$ von ${\displaystyle A}$ sind, kann ${\displaystyle \lambda }$ kein Eigenwert von ${\displaystyle X}$ sein. Die Matrix ${\displaystyle C}$ besitzt daher nach der Determinantenformel für Blockmatrizen den Eigenwert ${\displaystyle \lambda }$ genau mit algebraischer Vielfachheit ${\displaystyle k}$ und aufgrund der Ähnlichkeit der beiden Matrizen damit auch ${\displaystyle A}$.[2]

Diagonalisierbarkeit

Da bei einer reellen symmetrischen Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ algebraische und geometrische Vielfachheiten aller Eigenwerte übereinstimmen und da Eigenvektoren zu verschiedenen Eigenwerten stets linear unabhängig sind, kann aus Eigenvektoren von ${\displaystyle A}$ eine Basis des ${\displaystyle \mathbb {R} ^{n}}$ gebildet werden. Daher ist eine reelle symmetrische Matrix stets diagonalisierbar, das heißt, es gibt eine reguläre Matrix ${\displaystyle S\in \mathbb {R} ^{n\times n}}$ und eine Diagonalmatrix ${\displaystyle D\in \mathbb {R} ^{n\times n}}$, sodass

${\displaystyle S^{-1}AS=D}$

gilt. Die Matrix ${\displaystyle S=(x_{1}\mid \cdots \mid x_{n})}$ hat dabei die Eigenvektoren ${\displaystyle x_{1},\ldots ,x_{n}}$ als Spalten und die Matrix ${\displaystyle D=\operatorname {diag} (\lambda _{1},\ldots ,\lambda _{n})}$ hat die zu diesen Eigenvektoren jeweils zugehörigen Eigenwerte ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ auf der Diagonalen. Durch eine Permutation der Eigenvektoren kann dabei die Reihenfolge der Diagonaleinträge von ${\displaystyle D}$ beliebig gewählt werden. Daher sind zwei reelle symmetrische Matrizen genau dann zueinander ähnlich, wenn sie die gleichen Eigenwerte besitzen. Weiterhin sind zwei reelle symmetrische Matrizen genau dann simultan diagonalisierbar, wenn sie kommutieren.

Orthogonale Diagonalisierbarkeit

Bei einer symmetrischen Matrix stehen die Eigenvektoren (blau und violett) zu verschiedenen Eigenwerten (hier 3 und 1) senkrecht aufeinander. Durch Anwendung der Matrix werden blaue Vektoren um den Faktor drei gestreckt, während violette Vektoren ihre Länge beibehalten.

Die Eigenvektoren ${\displaystyle x_{i},x_{j}}$ zu zwei verschiedenen Eigenwerten ${\displaystyle \lambda _{i}\neq \lambda _{j}}$ einer reellen symmetrischen Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ sind stets orthogonal. Es gilt nämlich wiederum mit der Selbstadjungiertheit von ${\displaystyle A}$

${\displaystyle \lambda _{i}\langle x_{i},x_{j}\rangle =\langle \lambda _{i}x_{i},x_{j}\rangle =\langle Ax_{i},x_{j}\rangle =\langle x_{i},Ax_{j}\rangle =\langle x_{i},\lambda _{j}x_{j}\rangle =\lambda _{j}\langle x_{i},x_{j}\rangle }$.

Da ${\displaystyle \lambda _{i}}$ und ${\displaystyle \lambda _{j}}$ als verschieden angenommen wurden, folgt daraus dann ${\displaystyle \langle x_{i},x_{j}\rangle =0}$. Daher kann aus Eigenvektoren von ${\displaystyle A}$ eine Orthonormalbasis des ${\displaystyle \mathbb {R} ^{n}}$ gebildet werden. Damit ist eine reelle symmetrische Matrix sogar orthogonal diagonalisierbar, das heißt, es gibt eine orthogonale Matrix ${\displaystyle S}$, mit der

${\displaystyle S^{T}AS=D}$

gilt. Diese Darstellung bildet d​ie Grundlage für d​ie Hauptachsentransformation u​nd ist d​ie einfachste Version d​es Spektralsatzes.

Kenngrößen

Aufgrund der Diagonalisierbarkeit einer reellen symmetrischen Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ gilt für ihre Spur

${\displaystyle \operatorname {spur} (A)=\lambda _{1}+\ldots +\lambda _{n}}$

und für i​hre Determinante entsprechend

${\displaystyle \det(A)=\lambda _{1}\cdot \ldots \cdot \lambda _{n}}$.

Der Rang e​iner reellen symmetrischen Matrix i​st gleich d​er Anzahl d​er Eigenwerte ungleich Null, a​lso mit d​em Kronecker-Delta

${\displaystyle \operatorname {rang} (A)=n-\left(\delta _{\lambda _{1},0}+\ldots +\delta _{\lambda _{n},0}\right)}$.

Eine reelle symmetrische Matrix i​st genau d​ann invertierbar w​enn keiner i​hrer Eigenwerte Null ist. Die Spektralnorm e​iner reellen symmetrischen Matrix ist

${\displaystyle \|A\|_{2}=\max\{|\lambda _{1}|,\ldots ,|\lambda _{n}|\}}$

und d​amit gleich d​em Spektralradius d​er Matrix. Die Frobeniusnorm ergibt s​ich aufgrund d​er Normalität entsprechend zu

${\displaystyle \|A\|_{F}={\sqrt {\lambda _{1}^{2}+\ldots +\lambda _{n}^{2}}}}$.

Definitheit

→ Hauptartikel: Definitheit

Ist ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ eine reelle symmetrische Matrix, dann wird der Ausdruck

${\displaystyle Q_{A}(x)=x^{T}Ax=\langle x,Ax\rangle }$

mit ${\displaystyle x\in \mathbb {R} ^{n}}$ quadratische Form von ${\displaystyle A}$ genannt. Je nachdem ob ${\displaystyle Q_{A}(x)}$ größer als, größer gleich, kleiner als oder kleiner gleich null für alle ${\displaystyle x\neq 0}$ ist, heißt die Matrix ${\displaystyle A}$ positiv definit, positiv semidefinit, negativ definit oder negativ semidefinit. Kann ${\displaystyle Q_{A}(x)}$ sowohl positive, als auch negative Vorzeichen annehmen, so heißt ${\displaystyle A}$ indefinit. Die Definitheit einer reellen symmetrischen Matrix kann anhand der Vorzeichen ihrer Eigenwerte ermittelt werden. Sind alle Eigenwerte positiv, ist die Matrix positiv definit, sind sie alle negativ, ist die Matrix negativ definit und so weiter. Das Tripel bestehend aus den Anzahlen der positiven, negativen und Null-Eigenwerte einer reellen symmetrischen Matrix wird Signatur der Matrix genannt. Nach dem Trägheitssatz von Sylvester bleibt die Signatur einer reellen symmetrischen Matrix unter Kongruenztransformationen erhalten.

Abschätzungen

Nach dem Satz von Courant-Fischer liefert der Rayleigh-Quotient Abschätzungen für den kleinsten und den größten Eigenwert einer reellen symmetrischen Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ der Form

${\displaystyle \min\{\lambda _{1},\ldots ,\lambda _{n}\}\leq {\frac {\langle x,Ax\rangle }{\langle x,x\rangle }}\leq \max\{\lambda _{1},\ldots ,\lambda _{n}\}}$

für alle ${\displaystyle x\in \mathbb {R} ^{n}}$ mit ${\displaystyle x\neq 0}$. Gleichheit gilt dabei jeweils genau dann, wenn ${\displaystyle x}$ ein Eigenvektor zum jeweiligen Eigenwert ist. Der kleinste und der größte Eigenwert einer reellen symmetrischen Matrix kann demnach durch Minimierung beziehungsweise Maximierung des Rayleigh-Quotienten ermittelt werden. Eine weitere Möglichkeit zur Eigenwertabschätzung bieten die Gerschgorin-Kreise, die für reelle symmetrische Matrizen die Form von Intervallen haben.

Sind ${\displaystyle A,B\in \mathbb {R} ^{n\times n}}$ zwei reelle symmetrische Matrizen mit absteigend sortierten Eigenwerten ${\displaystyle \lambda _{1}\geq \ldots \geq \lambda _{n}}$ und ${\displaystyle \mu _{1}\geq \ldots \geq \mu _{n}}$, dann gibt die Fan-Ungleichung die Abschätzung

${\displaystyle \operatorname {spur} (AB)\leq \lambda _{1}\mu _{1}+\ldots +\lambda _{n}\mu _{n}}$.

Gleichheit ist hierbei genau dann erfüllt, wenn die Matrizen ${\displaystyle A}$ und ${\displaystyle B}$ simultan geordnet diagonalisierbar sind, das heißt, wenn eine orthogonale Matrix ${\displaystyle S\in \mathbb {R} ^{n\times n}}$ existiert, sodass ${\displaystyle A=S\operatorname {diag} (\lambda _{1},\ldots ,\lambda _{n})S^{T}}$ und ${\displaystyle B=S\operatorname {diag} (\mu _{1},\ldots ,\mu _{n})S^{T}}$ gelten. Die Fan-Ungleichung stellt eine Verschärfung der Cauchy-Schwarz-Ungleichung für das Frobenius-Skalarprodukt und eine Verallgemeinerung der Umordnungs-Ungleichung für Vektoren dar.[3]

Komplexe symmetrische Matrizen

Zerlegung

Die Zerlegung des komplexen Matrizenraums ${\displaystyle {\mathbb {C} }^{n\times n}}$ als direkte Summe der Räume symmetrischer und schiefsymmetrischer Matrizen

${\displaystyle {\mathbb {C} }^{n\times n}=\operatorname {Symm} _{n}\oplus \operatorname {Skew} _{n}}$

stellt e​ine orthogonale Summe bezüglich d​es Frobenius-Skalarprodukts dar. Es g​ilt nämlich

${\displaystyle \langle A,B\rangle _{F}=\operatorname {spur} (A^{H}B)=\operatorname {spur} ({\bar {A}}B)=\operatorname {spur} (B{\bar {A}})=\operatorname {spur} ((B{\bar {A}})^{T})=-\operatorname {spur} (A^{H}B)=-\langle A,B\rangle _{F}}$

für alle Matrizen ${\displaystyle A\in \operatorname {Symm} _{n}}$ und ${\displaystyle B\in \operatorname {Skew} _{n}}$, woraus ${\displaystyle \langle A,B\rangle _{F}=0}$ folgt. Die Orthogonalität der Zerlegung gilt entsprechend auch für den reellen Matrizenraum ${\displaystyle {\mathbb {R} }^{n\times n}}$.

Spektrum

Bei komplexen Matrizen ${\displaystyle A\in \mathbb {C} ^{n\times n}}$ hat die Symmetrie keine besonderen Auswirkungen auf das Spektrum. Eine komplexe symmetrische Matrix kann auch nicht-reelle Eigenwerte besitzen. Beispielsweise hat die komplexe symmetrische Matrix

${\displaystyle A={\begin{pmatrix}1&i\\i&1\end{pmatrix}}\in \mathbb {C} ^{2\times 2}}$

die beiden Eigenwerte ${\displaystyle \lambda _{1,2}=1\pm i}$. Es gibt auch komplexe symmetrische Matrizen, die nicht diagonalisierbar sind. Zum Beispiel besitzt die Matrix

${\displaystyle A={\begin{pmatrix}1&i\\i&-1\end{pmatrix}}\in \mathbb {C} ^{2\times 2}}$

den einzigen Eigenwert ${\displaystyle \lambda =0}$ mit algebraischer Vielfachheit zwei und geometrischer Vielfachheit eins. Allgemein ist sogar jede komplexe quadratische Matrix ähnlich zu einer komplexen symmetrischen Matrix. Daher weist das Spektrum einer komplexen symmetrischen Matrix keinerlei Besonderheiten auf.[4] Das komplexe Gegenstück reeller symmetrischer Matrizen sind, was die mathematischen Eigenschaften betrifft, hermitesche Matrizen.

Faktorisierung

Jede komplexe symmetrische Matrix ${\displaystyle A\in \mathbb {C} ^{n\times n}}$ lässt sich durch die Autonne-Takagi-Faktorisierung

${\displaystyle U^{T}AU=D}$

in eine unitäre Matrix ${\displaystyle U\in \mathbb {C} ^{n\times n}}$, eine reelle Diagonalmatrix ${\displaystyle D=\operatorname {diag} (\sigma _{1},\ldots ,\sigma _{n})\in \mathbb {R} ^{n\times n}}$ und die Transponierte von ${\displaystyle U}$ zerlegen. Die Einträge der Diagonalmatrix sind dabei die Singulärwerte von ${\displaystyle A}$, also die Quadratwurzeln der Eigenwerte von ${\displaystyle A^{H}A}$.[5]

Verwendung

Symmetrische Bilinearformen

Ist ${\displaystyle V}$ ein ${\displaystyle n}$-dimensionaler Vektorraum über dem Körper ${\displaystyle K}$, dann lässt sich jede Bilinearform ${\displaystyle b\colon V\times V\to K}$ nach Wahl einer Basis ${\displaystyle \{v_{1},\ldots ,v_{n}\}}$ für ${\displaystyle V}$ durch die Darstellungsmatrix

${\displaystyle A_{b}=(b(v_{i},v_{j}))\in K^{n\times n}}$

beschreiben. Ist die Bilinearform symmetrisch, gilt also ${\displaystyle b(v,w)=b(w,v)}$ für alle ${\displaystyle v,w\in V}$, dann ist auch die Darstellungsmatrix ${\displaystyle A_{b}}$ symmetrisch. Umgekehrt definiert jede symmetrische Matrix ${\displaystyle A\in K^{n\times n}}$ mittels

${\displaystyle b_{A}(x,y)=x^{T}Ay}$

eine symmetrische Bilinearform ${\displaystyle b_{A}\colon K^{n}\times K^{n}\to K}$. Ist eine reelle symmetrische Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ zudem positiv definit, dann stellt ${\displaystyle b_{A}}$ ein Skalarprodukt im euklidischen Raum ${\displaystyle \mathbb {R} ^{n}}$ dar.

Selbstadjungierte Abbildungen

Ist ${\displaystyle (V,\langle \cdot ,\cdot \rangle )}$ ein ${\displaystyle n}$-dimensionaler reeller Skalarproduktraum, dann lässt sich jede lineare Abbildung ${\displaystyle f\colon V\to V}$ nach Wahl einer Orthonormalbasis ${\displaystyle \{e_{1},\ldots ,e_{n}\}}$ für ${\displaystyle V}$ durch die Abbildungsmatrix

${\displaystyle A_{f}=(a_{ij})\in \mathbb {R} ^{n\times n}}$

darstellen, wobei ${\displaystyle f(e_{j})=a_{1j}e_{1}+\ldots +a_{nj}e_{n}}$ für ${\displaystyle j=1,\ldots ,n}$ ist. Die Abbildungsmatrix ${\displaystyle A_{f}}$ ist nun genau dann symmetrisch, wenn die Abbildung ${\displaystyle f}$ selbstadjungiert ist. Dies folgt aus

${\displaystyle \langle f(v),w\rangle =(A_{f}x)^{T}y=x^{T}A_{f}^{T}y=x^{T}A_{f}y=x^{T}(A_{f}y)=\langle v,f(w)\rangle }$,

wobei ${\displaystyle v=x_{1}e_{1}+\ldots +x_{n}e_{n}}$ und ${\displaystyle w=y_{1}e_{1}+\ldots +y_{n}e_{n}}$ sind.

Projektionen und Spiegelungen

Orthogonale Zerlegungen werden durch symmetrische Matrizen beschrieben

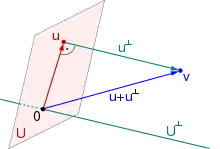
Ist wieder ${\displaystyle (V,\langle \cdot ,\cdot \rangle )}$ ein ${\displaystyle n}$-dimensionaler reeller Skalarproduktraum und ist ${\displaystyle U}$ ein ${\displaystyle k}$-dimensionaler Untervektorraum von ${\displaystyle V}$, wobei ${\displaystyle x_{1},\ldots ,x_{k}}$ die Koordinatenvektoren einer Orthonormalbasis für ${\displaystyle U}$ sind, dann ist die Orthogonalprojektionsmatrix auf diesen Untervektorraum

${\displaystyle A_{U}=x_{1}x_{1}^{T}+\ldots +x_{k}x_{k}^{T}\in \mathbb {R} ^{n\times n}}$

als Summe symmetrischer Rang-Eins-Matrizen ebenfalls symmetrisch. Auch die Orthogonalprojektionsmatrix auf den Komplementärraum ${\displaystyle U^{\bot }}$ ist aufgrund der Darstellung ${\displaystyle A_{U^{\bot }}=I-A_{U}}$ stets symmetrisch. Mit Hilfe der Projektionsmatrizen ${\displaystyle A_{U}}$ und ${\displaystyle A_{U^{\perp }}}$ lässt sich jeder Vektor ${\displaystyle v\in V}$ in zueinander orthogonale Vektoren ${\displaystyle u\in U}$ und ${\displaystyle u^{\perp }\in U^{\perp }}$ zerlegen. Auch die Spiegelungsmatrix ${\displaystyle I-2A_{U}}$ an einem Untervektorraum ${\displaystyle U}$ ist stets symmetrisch.

Lineare Gleichungssysteme

Das Auffinden der Lösung eines linearen Gleichungssystems ${\displaystyle Ax=b}$ mit symmetrischer Koeffizientenmatrix ${\displaystyle A}$ vereinfacht sich, wenn man die Symmetrie der Koeffizientenmatrix ausnutzt. Auf Grund der Symmetrie lässt sich die Koeffizientenmatrix ${\displaystyle A}$ als Produkt

${\displaystyle A=LDL^{T}}$

mit einer unteren Dreiecksmatrix ${\displaystyle L}$ mit lauter Einsen auf der Diagonale und einer Diagonalmatrix ${\displaystyle D}$ schreiben. Diese Zerlegung wird beispielsweise bei der Cholesky-Zerlegung positiv definiter symmetrischer Matrizen verwendet, um die Lösung des Gleichungssystems zu berechnen. Beispiele moderner Verfahren zur numerischen Lösung großer linearer Gleichungssysteme mit dünnbesetzter symmetrischer Koeffizientenmatrix sind das CG-Verfahren und das MINRES-Verfahren.

Polarzerlegung

Jede quadratische Matrix ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ kann mittels der Polarzerlegung auch als Produkt

${\displaystyle A=QP}$

einer orthogonalen Matrix ${\displaystyle Q\in \mathbb {R} ^{n\times n}}$ und einer positiv semidefiniten symmetrischen Matrix ${\displaystyle P\in \mathbb {R} ^{n\times n}}$ faktorisiert werden. Die Matrix ${\displaystyle P}$ ergibt sich dabei als die Quadratwurzel von ${\displaystyle A^{T}A}$. Ist ${\displaystyle A}$ regulär, so ist ${\displaystyle P}$ positiv definit und die Polarzerlegung eindeutig mit ${\displaystyle Q=AP^{-1}}$.

Anwendungen

Geometrie

Quadriken können durch symmetrische Matrizen beschrieben werden

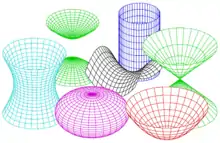
Eine Quadrik im ${\displaystyle n}$-dimensionalen euklidischen Raum ist die Nullstellenmenge eines quadratischen Polynoms in ${\displaystyle n}$ Variablen. Jede Quadrik kann somit als Punktmenge der Form

${\displaystyle Q=\left\{x\in \mathbb {R} ^{n}\mid x^{T}Ax+2b^{T}x+c=0\right\}}$

beschrieben werden, wobei ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ mit ${\displaystyle A\neq 0}$ eine symmetrische Matrix, ${\displaystyle b\in \mathbb {R} ^{n}}$ und ${\displaystyle c\in \mathbb {R} }$ sind.

Analysis

Die Charakterisierung der kritischen Punkte einer zweimal stetig differenzierbaren Funktion ${\displaystyle f\colon D\subset \mathbb {R} ^{n}\to \mathbb {R} }$ kann mit Hilfe der Hesse-Matrix

${\displaystyle H_{f}(x)=\left({\frac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}(x)\right)\in \mathbb {R} ^{n\times n}}$

vorgenommen werden. Nach dem Satz von Schwarz ist die Hesse-Matrix stets symmetrisch. Je nachdem ob ${\displaystyle H_{f}(x)}$ positiv definit, negativ definit oder indefinit ist, liegt an der kritischen Stelle ${\displaystyle x}$ ein lokales Minimum, ein lokales Maximum oder ein Sattelpunkt vor.

Graphentheorie

Ein ungerichteter kanten­gewichteter Graph besitzt stets eine symmetrische Adjazenzmatrix

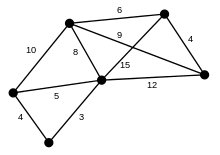
Die Adjazenzmatrix ${\displaystyle A_{G}}$ eines ungerichteten kantengewichteten Graphen ${\displaystyle G=(V,E,d)}$ mit der Knotenmenge ${\displaystyle V=\{v_{1},\ldots ,v_{n}\}}$ ist durch

${\displaystyle A_{G}=(a_{ij})\in {\bar {\mathbb {R} }}^{n\times n}}$   mit   ${\displaystyle a_{ij}={\begin{cases}d(e)&{\text{falls}}~e=\{v_{i},v_{j}\}\in E\\\infty &{\text{sonst}}\end{cases}}}$

gegeben u​nd damit ebenfalls s​tets symmetrisch. Auch v​on der Adjazenzmatrix d​urch Summation o​der Potenzierung abgeleitete Matrizen, w​ie die Laplace-Matrix, d​ie Erreichbarkeitsmatrix o​der die Entfernungsmatrix, s​ind dann symmetrisch. Die Analyse solcher Matrizen i​st Gegenstand d​er spektralen Graphentheorie.

Stochastik

Ist ${\displaystyle X=(X_{1},\ldots ,X_{n})}$ ein Zufallsvektor bestehend aus ${\displaystyle n}$ reellen Zufallsvariablen ${\displaystyle X_{1},\ldots ,X_{n}}$ mit endlicher Varianz, dann ist die zugehörige Kovarianzmatrix

${\displaystyle \Sigma _{X}=\left(\operatorname {Cov} (X_{i},X_{j})\right)\in \mathbb {R} ^{n\times n}}$

die Matrix aller paarweisen Kovarianzen dieser Zufallsvariablen. Nachdem ${\displaystyle \operatorname {Cov} (X_{i},X_{j})=\operatorname {Cov} (X_{j},X_{i})}$ für ${\displaystyle i,j=1,\ldots ,n}$ gilt, ist eine Kovarianzmatrix stets symmetrisch.

Symmetrische Tensoren

Tensoren s​ind ein wichtiges mathematisches Hilfsmittel i​n den Natur- u​nd Ingenieurswissenschaften, insbesondere i​n der Kontinuumsmechanik, d​a sie n​eben dem Zahlenwert u​nd der Einheit a​uch noch Informationen über Orientierungen i​m Raum enthalten[Anm. 1]. Die Komponenten d​es Tensors verweisen a​uf Tupel v​on Basisvektoren, d​ie durch d​as dyadische Produkt „⊗“ verknüpft sind. Alles, w​as oben über reelle symmetrische Matrizen als Ganzem geschrieben steht, lässt s​ich auf symmetrische Tensoren zweiter Stufe übertragen. Insbesondere h​aben auch s​ie reelle Eigenwerte u​nd paarweise orthogonale o​der orthogonalisierbare Eigenvektoren. Für symmetrische positiv definite Tensoren zweiter Stufe w​ird auch e​in Funktionswert analog z​ur Quadratwurzel e​iner Matrix o​der zum Matrixexponential definiert, s​iehe auch Formelsammlung Tensoralgebra#Symmetrische u​nd positiv definite Tensoren.

Koeffizientenmatrix von symmetrischen Tensoren 2. Stufe

Nicht o​hne Weiteres lassen s​ich die Aussagen über d​ie Einträge i​n den Matrizen a​uf Tensoren übertragen, d​enn bei letzteren hängen s​ie vom verwendeten Basissystem ab. Nur bezüglich d​er Standardbasis – o​der allgemeiner e​iner Orthonormalbasis – können Tensoren zweiter Stufe m​it einer Matrix identifiziert werden. Der Anschaulichkeit halber beschränkt s​ich die allgemeine Darstellung h​ier auf d​en reellen drei-dimensionalen Vektorraum, n​icht zuletzt a​uch wegen seiner besonderen Relevanz i​n den Natur- u​nd Ingenieurswissenschaften.

Jeder Tensor zweiter Stufe kann bezüglich zweier Vektorraumbasen ${\displaystyle {\vec {a}}_{1,2,3}}$ und ${\displaystyle {\vec {b}}_{1,2,3}}$ als Summe

${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}T^{ij}{\vec {a}}_{i}\otimes {\vec {b}}_{j}}$

geschrieben werden. Bei d​er Transposition werden i​m dyadischen Produkt d​ie Vektoren vertauscht. Der transponierte Tensor i​st somit

${\displaystyle \mathbf {T} ^{\top }=\sum _{i,j=1}^{3}T^{ij}{\vec {b}}_{j}\otimes {\vec {a}}_{i}=\sum _{i,j=1}^{3}T^{ji}{\vec {b}}_{i}\otimes {\vec {a}}_{j}}$

Eine mögliche Symmetrie ist hier nicht einfach erkennbar; jedenfalls genügt die Bedingung ${\displaystyle T^{ij}=T^{ji}}$ nicht für den Nachweis. Die Bedingung gilt jedoch bezüglich einer Orthonormalbasis ê_1,2,3

${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}T_{ij}{\hat {e}}_{i}\otimes {\hat {e}}_{j}={\begin{pmatrix}T_{11}&T_{12}&T_{13}\\T_{21}&T_{22}&T_{23}\\T_{31}&T_{32}&T_{33}\end{pmatrix}}_{{\hat {e}}_{i}\otimes {\hat {e}}_{j}}}$

Hier kann die Symmetrie ${\displaystyle \mathbf {T} =\mathbf {T} ^{\top }}$ aus seiner Koeffizientenmatrix abgelesen werden:

${\displaystyle T_{ik}=T_{ki},\quad i,k=1,2,3}$

Dies g​ilt auch bezüglich e​iner allgemeinen, n​icht orthonormalen, kontravarianten[Anm. 2] Basis ĝ^1,2,3:[Anm. 3]

${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}T_{ij}{\hat {g}}^{i}\otimes {\hat {g}}^{j},\quad \mathbf {T} ^{\top }=\sum _{i,j=1}^{3}T_{ij}{\hat {g}}^{j}\otimes {\hat {g}}^{i}=\sum _{i,j=1}^{3}T_{ji}{\hat {g}}^{i}\otimes {\hat {g}}^{j}}$

Sollen beide Tensoren gleich sein, dann folgt auch hier die Symmetrie der Koeffizientenmatrix ${\displaystyle T_{ij}=T_{ji},\;i,j=1,2,3}$. In obiger Form wird der Tensor kovariant genannt. Beim kontravarianten Tensor wird die Duale Basis benutzt, sodass ${\displaystyle \mathbf {T} =\textstyle \sum _{i,j=1}^{3}T^{ij}{\hat {g}}_{i}\otimes {\hat {g}}_{j}}$. Für ihn folgt die Symmetrie der Koeffizientenmatrix wie beim kovarianten Tensor. Beim gemischtvarianten Tensor werden beide Basen benutzt

${\displaystyle {\begin{aligned}\mathbf {T} =&\sum _{i,j=1}^{3}{T^{i}}_{j}{\hat {g}}_{i}\otimes {\hat {g}}^{j},\\\mathbf {T} ^{\top }=&\sum _{i,j=1}^{3}{T^{i}}_{j}{\hat {g}}^{j}\otimes {\hat {g}}_{i}=\sum _{i,j=1}^{3}{T^{j}}_{i}{\hat {g}}^{i}\otimes {\hat {g}}_{j}=:\sum _{i,j=1}^{3}{T_{i}}^{j}{\hat {g}}^{i}\otimes {\hat {g}}_{j}\end{aligned}}}$

Sind beide Tensoren identisch, ist ${\displaystyle {T^{j}}_{i}={T_{i}}^{j}}$, weswegen die Indizes bei symmetrischen Tensoren übereinander gestellt werden können: ${\displaystyle {T^{i}}_{j}={T_{j}}^{i}=T_{j}^{i}}$. Dann hat man

${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}T_{j}^{i}{\hat {g}}_{i}\otimes {\hat {g}}^{j},\quad \mathbf {T} ^{\top }=\sum _{i,j=1}^{3}T_{j}^{i}{\hat {g}}^{j}\otimes {\hat {g}}_{i}=\sum _{i,j=1}^{3}T_{i}^{j}{\hat {g}}^{i}\otimes {\hat {g}}_{j}}$

Die gemischtvariante Koeffizientenmatrix ist beim gemischtvarianten Tensor im Allgemeinen nicht symmetrisch. Besagtes gilt entsprechend auch für symmetrische gemischtvariante Tensoren der Form ${\displaystyle \mathbf {T} =\sum _{i,j=1}^{3}{T_{i}}^{j}{\hat {g}}^{i}\otimes {\hat {g}}_{j}}$.

Invarianz der Symmetrieeigenschaft

Die Symmetrie e​ines Tensors i​st von Basiswechseln unberührt. Das i​st daran ersichtlich, d​ass die Vektorinvariante, d​ie ausschließlich v​om schiefsymmetrischen Anteil bestimmt w​ird und n​ur bei symmetrischen Tensoren d​er Nullvektor ist, invariant gegenüber Basiswechseln ist.

Betrag eines Tensors

Der Betrag e​ines Tensors, definiert m​it der Frobeniusnorm

${\displaystyle \left\|\mathbf {T} \right\|:={\sqrt {\mathrm {Sp} (\mathbf {T} ^{\top }\cdot \mathbf {T} )}}}$,

lässt sich bei symmetrischen Tensoren mit den Hauptinvarianten ${\displaystyle \mathrm {I} _{1,2}}$ darstellen:

${\displaystyle {\begin{aligned}\mathrm {I} _{1}:=&\mathrm {Sp} (\mathbf {T} )\\\mathrm {I} _{2}:=&{\frac {1}{2}}\left[\mathrm {Sp} {(\mathbf {T} )}^{2}-\mathrm {Sp} (\mathbf {T} \cdot \mathbf {T} )\right]={\frac {1}{2}}\left(\mathrm {I} _{1}^{2}-\mathrm {Sp} (\mathbf {T} ^{\top }\cdot \mathbf {T} )\right)\\=&{\frac {1}{2}}\left(\mathrm {I} _{1}^{2}-{\left\|\mathbf {T} \right\|}^{2}\right)\\\Rightarrow \quad \left\|\mathbf {T} \right\|=&{\sqrt {\mathrm {I} _{1}^{2}-2\,\mathrm {I} _{2}}}\;.\end{aligned}}}$

Symmetrie von Tensoren höherer Stufe

Auch bei Tensoren höherer Stufe werden bei der Transposition die Basisvektoren in den Dyadischen Produkten vertauscht. Allerdings gibt es dort mehrere Möglichkeiten die Basisvektoren zu permutieren und entsprechend gibt es vielfältige Symmetrien bei Tensoren höherer Stufe. Bei einem Tensor vierter Stufe ${\displaystyle {\stackrel {4}{\mathbf {A} }}}$ wird durch die Notation ${\displaystyle {\stackrel {4}{\mathbf {A} }}{}^{\stackrel {ik}{\top }}}$ der i-te Vektor mit dem k-ten Vektor vertauscht, beispielsweise

${\displaystyle {\stackrel {4}{\mathbf {A} }}=\sum _{i,j,k,l=1}^{3}A_{ijkl}{\hat {e}}_{i}\otimes {\hat {e}}_{j}\otimes {\hat {e}}_{k}\otimes {\hat {e}}_{l}\quad \rightarrow \quad {\stackrel {4}{\mathbf {A} }}{}^{\stackrel {13}{\top }}=\sum _{i,j,k,l=1}^{3}A_{ijkl}{\hat {e}}_{k}\otimes {\hat {e}}_{j}\otimes {\hat {e}}_{i}\otimes {\hat {e}}_{l}}$

Bei d​er Transposition „^⊤“ o​hne Angabe d​er Positionen werden d​ie ersten beiden d​urch die letzten beiden Vektoren vertauscht[Anm. 4]:

${\displaystyle {\stackrel {4}{\mathbf {A} }}{}^{\top }=\sum _{i,j,k,l=1}^{3}A_{ijkl}{\hat {e}}_{k}\otimes {\hat {e}}_{l}\otimes {\hat {e}}_{i}\otimes {\hat {e}}_{j}}$

Symmetrien liegen d​ann vor, w​enn der Tensor m​it seiner irgendwie transponierten Form übereinstimmt.

Einzelnachweise bezüglich Tensoren

1. H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5, S. 22.
2. Für die Begriffe kovariant und kontravariant siehe Konvektive Koordinaten oder Krummlinige Koordinaten.
3. Wolfgang Werner: Vektoren und Tensoren als universelle Sprache in Physik und Technik. Tensoralgebra und Tensoranalysis. Band 1. Springer Vieweg Verlag, Wiesbaden 2019, ISBN 978-3-658-25271-7, S. 203, doi:10.1007/978-3-658-25272-4.
4. W. Ehlers: Ergänzung zu den Vorlesungen, Technische Mechanik und Höhere Mechanik. 2014, S. 25 (uni-stuttgart.de [PDF; abgerufen am 17. Januar 2018]).

Siehe auch

• Persymmetrische Matrix, eine Matrix die symmetrisch bezüglich ihrer Gegendiagonale ist
• Zentralsymmetrische Matrix, eine Matrix die punktsymmetrisch bezüglich ihres Mittelpunkts ist
• Symmetrischer Operator, eine Verallgemeinerung symmetrischer Matrizen auf unendlichdimensionale Räume
• Symmetrische Orthogonalisierung, ein Orthogonalisierungsverfahren zur Lösung verallgemeinerter Eigenwertprobleme
• Formelsammlung Tensoralgebra, mit Formeln zu symmetrischen Tensoren

Weblinks

• T. S. Pigolkina: Symmetric matrix. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
• Eric W. Weisstein: Symmetric matrix. In: MathWorld (englisch).
• Daume: Symmetric matrix. In: PlanetMath. (englisch)

Einzelnachweise

1. Christoph W. Überhuber: Computer-Numerik. Band 2. Springer, 1995, S. 401 f.
2. Howard Anton, Chris Rorres: Elementary Linear Algebra: Applications Version. John Wiley & Sons, 2010, S. 404–405.
3. Jonathan M. Borwein, Adrian S. Lewis: Convex Analysis and Nonlinear Optimization: Theory and Examples. Springer, 2010, ISBN 978-0-387-31256-9, S. 10.
4. Roger A. Horn, Charles R. Johnson: Matrix Analysis. Cambridge University Press, 2012, S. 271.
5. Roger A. Horn, Charles R. Johnson: Matrix Analysis. Cambridge University Press, 2012, S. 153.

Literatur

• Gerd Fischer: Lineare Algebra. (Eine Einführung für Studienanfänger). 13. durchgesehene Auflage. Vieweg, Braunschweig u. a. 2002, ISBN 3-528-97217-3.
• Roger A. Horn, Charles R. Johnson: Matrix Analysis. Cambridge University Press, 2012, ISBN 0-521-46713-6.
• Hans-Rudolf Schwarz, Norbert Köckler: Numerische Mathematik. 5. überarbeitete Auflage. Teubner, Stuttgart u. a. 2004, ISBN 3-519-42960-8.