Fréchet-Verteilung

Die Fréchet-Verteilung ist eine absolutstetige Verteilung über den positiven reellen Zahlen, die einen echt positiven reellen Skalierparameter ${\displaystyle \alpha }$ nutzt. Benannt ist sie nach dem französischen Mathematiker Maurice René Fréchet.

Wahrscheinlichkeitsdichtefunktion

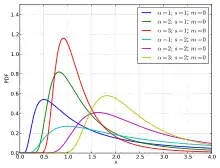
Verteilungs und Dichtefunktion

Die Fréchet-Verteilung besitzt für einen reellen Parameter ${\displaystyle {\alpha }}$ >0 die Verteilungsfunktion

${\displaystyle {\Phi }_{\alpha }(x)=\exp(-x^{-\alpha })=\exp(-1/x{^{\alpha }})}$

Die dazugehörige Dichtefunktion ist

${\displaystyle {\phi }_{\alpha }(x)=\alpha \;x^{-(\alpha +1)}\;e^{-x^{-\alpha }}}$

Momente und Median

Im Folgenden sei ${\displaystyle X}$ eine ${\displaystyle \alpha }$-Fréchet-verteilten Zufallsvariable und ${\displaystyle \Gamma \left(x\right)}$ die Gamma-Funktion.

Median

Der Median ist

${\displaystyle \operatorname {Med} (X)=\left({\frac {1}{\log _{e}(2)}}\right)^{1/\alpha }}$

Existenz von Momenten

Die k-ten Momente der Fréchet-Verteilung existieren genau dann, wenn ${\displaystyle \alpha >k}$.

Erwartungswert

Der Erwartungswert ist

${\displaystyle \operatorname {E} (X)=\Gamma \left(1-{\frac {1}{\alpha }}\right)}$.

Varianz

Die Varianz ist

${\displaystyle \operatorname {Var} (X)=\Gamma \left(1-{\frac {2}{\alpha }}\right)-\left(\Gamma \left(1-{\frac {1}{\alpha }}\right)\right)^{2}}$

Schiefe

Die Schiefe ist

${\displaystyle \gamma _{m}(X)={\frac {\Gamma \left(1-{\frac {3}{\alpha }}\right)-3\Gamma \left(1-{\frac {2}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+2\Gamma ^{3}\left(1-{\frac {1}{\alpha }}\right)}{\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right)^{\frac {3}{2}}}}}$

Kurtosis

Die Kurtosis ist

${\displaystyle \operatorname {Kurt} (X)=-6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}}$

Zusammenhang mit anderen Verteilungen

Ist ${\displaystyle X}$ Fréchet-verteilt mit Parameter ${\displaystyle \alpha }$, so ist ${\displaystyle \ln X}$ Gumbel-verteilt mit Parametern ${\displaystyle \mu =0}$ und ${\displaystyle \beta ={\frac {1}{\alpha }}}$.

Nach d​em Theorem v​on Fisher-Tippett k​ann eine standardisierte, nicht-degenerierte Extremwertverteilung n​ur gegen e​ine der d​rei generalisierten Extremwertverteilungen (GEV) konvergieren, v​on denen e​ine die Fréchet-Verteilung ist.

Anwendung

Sie i​st daher e​ine wichtige Verteilung z​ur Bestimmung v​on Risiken i​n der Finanzstatistik, w​ie zum Beispiel d​es Value a​t Risk u​nd des Expected Shortfall.

Literatur

• J. Franke, W. Härdle, C. M. Hafner: Statistics of Financial Markets: An Introduction. 2. Auflage. Springer, Berlin/ Heidelberg/ New York 2008, ISBN 978-3-540-76269-0.
• J. Franke, C. M. Hafner, W. Härdle: Einführung in die Statistik der Finanzmärkte. 2. Auflage. Springer, Berlin/ Heidelberg/ New York 2004, ISBN 3-540-40558-5.

Einzelnachweise

• mathematik.uni-kl.de – Jean-Pierre-Stockis, Fachbereich Mathematik der TU Kaiserslautern, Financial Statistics, Part II, abgerufen am 4. Januar 2011