Voigt-Profil

Unter dem Voigt-Profil oder auch der Voigtfunktion (nach Woldemar Voigt) versteht man die Faltung einer Gauß-Kurve ${\displaystyle G(x)}$ mit einer Lorentz-Kurve ${\displaystyle L(x)}$.

Verschiedene Voigt-Profile jeweils mit Halbwertsbreite 2. Spezialfälle sind die Lorentz-Kurve (blau) und die Gauß-Kurve (grün).

Mathematische Beschreibung

${\displaystyle V(x;\sigma ,\gamma )=(G*L)(x)=\int G(\tau )L(x-\tau )d\tau }$

${\displaystyle G(x;\sigma )={\frac {e^{-x^{2}/(2\sigma ^{2})}}{\sigma {\sqrt {2\pi }}}}}$

${\displaystyle L(x;\gamma )={\frac {\gamma }{\pi (x^{2}+\gamma ^{2})}}.}$

${\displaystyle \sigma }$ entspricht der Standardabweichung einer Gauß-Verteilung. In der Spektroskopie wird sie als Dopplerbreite bezeichnet. ${\displaystyle \gamma }$ ist die halbe Halbwertsbreite der Lorentzverteilung, in der Spektroskopie als Druckverbreitung bekannt. Das Voigt-Profil entsteht aus der Faltung des Gauß-Profils mit dem Lorentz-Profil. Das Voigt-Profil ist wie jeweils das Gauß- und Lorentz-Profil auf 1 normiert (Fläche unter den Profilen).

Numerische Darstellung

Für das Faltungsintegral ${\displaystyle V(x)}$ existiert keine analytische Lösung, doch kann es als Realteil der Faddeeva-Funktion ${\displaystyle w(z)}$ (skalierte komplexe Fehlerfunktion, Plasma-Dispersionsfunktion) ausgedrückt werden, für die hinreichend gute Näherungen verfügbar sind:

${\displaystyle V(x;\sigma ,\gamma )={\frac {\operatorname {Re} \left[w(z)\right]}{\sigma {\sqrt {2\pi }}}}.}$

${\displaystyle z}$ ist hier definiert als

${\displaystyle z={\frac {x+i\gamma }{\sigma {\sqrt {2}}}}.}$

Die Breite des Voigt-Profils

Die Halbwertsbreite d​es Voigt-Profils lässt s​ich aus d​en Breiten d​er beteiligten Lorentz- u​nd Gauß-Kurven bestimmen. Bekannt s​ind die Breiten d​es Gauß-Profils (fwhm: v​olle Breite b​ei halbem Maximum),

${\displaystyle f_{\mathrm {G} }={\sqrt {8\ln(2)}}\sigma ,}$

und d​es Lorentz-Profils,

${\displaystyle f_{\mathrm {L} }=2\gamma .}$

Die Breite des Voigt-Profils ${\displaystyle f_{\mathrm {V} }}$ ist eine Funktion von ${\displaystyle f_{\mathrm {G} }}$ und ${\displaystyle f_{\mathrm {L} }}$.

Die einfachste Näherung i​st die symmetrische Interpolationsformel[1]

${\displaystyle f_{\mathrm {V} }\approx {\sqrt {f_{\mathrm {G} }^{2}+f_{\mathrm {L} }^{2}}},}$

die jedoch ${\displaystyle f_{\mathrm {V} }}$ um bis zu 16 % unterschätzt.[2]

Eine bessere Näherung i​st nach Olivero a​nd Longbothum[3]

${\displaystyle f_{\mathrm {V} }\approx 0{,}5346f_{\mathrm {L} }+{\sqrt {0{,}2166f_{\mathrm {L} }^{2}+f_{\mathrm {G} }^{2}}}}$

mit e​iner maximalen Abweichung v​on 0,023%.

Eigenschaften

Die Voigt-Funktion i​st invariant gegenüber Faltung, d. h., d​ie Faltung e​iner Voigt-Funktion m​it einer weiteren Voigt-Funktion ergibt wieder e​ine Voigt-Funktion. Die Linienbreiten d​es Gauß- bzw. Lorentz-Anteils ergeben s​ich dabei zu:

${\displaystyle f_{\mathrm {G} }^{2}=\sum _{i}{(f_{\mathrm {G} }^{2})_{i}}}$

und

${\displaystyle f_{\mathrm {L} }=\sum _{i}{(f_{\mathrm {L} })_{i}}}$.

Näherung durch Pseudo-Voigt-Profil

Beim Vergleich zwischen Voigt-Profil (blau) und Pseudo-Voigt-Profil (magenta) sind kaum Unterschiede erkennbar.

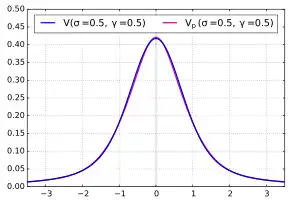
Das Pseudo-Voigt-Profil (oder die Pseudo-Voigt-Funktion) ist eine Näherungsfunktion für das Voigt-Profil, bei der die Faltung durch eine Linearkombination aus Gauß- und Lorentzkurve ersetzt wird. Es wird traditionell zur Ausgleichsrechnung von Röntgendiffraktometrie-Profilen verwendet. Seit eine effiziente und sehr genaue Implementierung der eigentlichen Voigt-Funktion zur Verfügung steht, gibt es keinen guten Grund mehr für die Verwendung dieser Näherung.

Mathematische Definition:

${\displaystyle V_{p}(x)=\eta \cdot L(x)+(1-\eta )\cdot G(x)\;}$   mit   ${\displaystyle 0<\eta <1}$

${\displaystyle G(x)=\exp {\left[-\ln(2)\cdot \left({\frac {x-x_{0}}{w}}\right)^{2}\right]}\;}$

${\displaystyle L(x)={\frac {1}{1+({\frac {x-x_{0}}{w}})^{2}}}}$

Dabei ist ${\displaystyle 2w}$ die Halbwertsbreite der Pseudo-Voigt-Funktion.

Beispiele

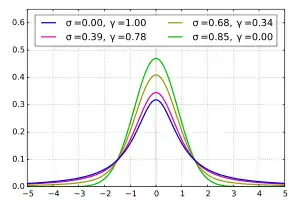
Bei einem großen Verhältnis zwischen Druck- und Dopplerverbreiterung ${\displaystyle \gamma /\sigma \gg 1}$ ist das Voigt-Profil mit dem Lorentz-Profil fast identisch. Nur unmittelbar an der Linienmitte tritt eine geringe Abrundung durch die Faltung mit der Gaußkurve auf. Liegt ${\displaystyle \gamma /\sigma }$ bei 1, wird der zentrale Teil der Linie durch das Gauß-Profil dominiert, man spricht dann vom Dopplerkern. Außen setzt sich jedoch das viel langsamer abfallende Lorentz-Profil durch, man bezeichnet diesen Bereich als Dämpfungsflügel. Im Falle ${\displaystyle \gamma /\sigma \ll 1}$ wird aus dem Voigt-Profil nahezu ein Gauß-Profil. Die logarithmische Darstellung (die Gaußkurve erscheint dann als Parabel) lässt jedoch erkennen, dass sehr weit von der Linienmitte entfernt immer noch das Lorentz-Profil hervortritt, allerdings dann auf sehr niedrigem Niveau.

Der Fall ${\displaystyle \gamma /\sigma \gg 1}$ entspricht durchwegs irdischen Bedingungen, denen etwa die Spektrallinien der in der Erdatmosphäre vorhandenen Moleküle unterworfen sind. Der Fall ${\displaystyle \gamma /\sigma =1}$ oder gar ${\displaystyle \gamma /\sigma \ll 1}$ setzt niedrige Drücke und hohe Temperaturen voraus, wie sie zumeist für Sternatmosphären charakteristisch sind.

Literatur

• Woldemar Voigt: Das Gesetz der Intensitätsverteilung innerhalb der Linien eines Gasspektrums. Sitzungsbericht der Bayerischen Akademie der Wissenschaften, Band 25, 1912, S. 603–620, (online).
• Z. Shippony, W. G. Read, A Highly Accurate Voigt Function Algorithm. In: Journal of Quantitative Spectroscopy & Radiative Transfer. Bd. 50, Nr. 6, 1993, ISSN 0022-4073, S. 635–645, doi:10.1016/0022-4073(93)90031-C; Erratum: A Correction to a Highly Accurate Voigt Function Algorithm. ebenda Bd. 78, Nr. 2, 2003, S. 255, doi:10.1016/S0022-4073(02)00169-3.

Einzelnachweise

1. Danos & Geshwind, Phys Rev91, 1159 (1953).
2. Ablesbar aus Fig. 1 in Olivero & Longbothom (1977)
3. J. J. Olivero, R. L. Longbothum: Empirical fits to the Voigt line width: A brief review. In: Journal of Quantitative Spectroscopy & Radiative Transfer. Bd. 17, Nr. 2, 1977, S. 233–236, doi:10.1016/0022-4073(77)90161-3.

Weblinks

• https://jugit.fz-juelich.de/mlz/libcerf, numerische C-Bibliothek für komplexe Fehlerfunktionen von Steven G. Johnson und Joachim Wuttke, enthält eine Funktion voigt (x, sigma, gamma) mit ungefähr 13-stelliger Genauigkeit.