Lévy-Verteilung

Lévy-Verteilungen (benannt n​ach dem französischen Mathematiker Paul Lévy) s​ind eine Familie v​on Wahrscheinlichkeitsverteilungen m​it der besonderen Eigenschaft e​ines jeweils unendlichen Erwartungswerts.

Definition

Lévy-Dichtefunktionen verschiedener Skalierung und μ=0

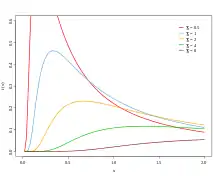
Die Dichtefunktion d​er Lévy-Verteilungen lautet

${\displaystyle f(x)={\sqrt {\frac {\gamma }{2\pi }}}\cdot {\frac {1}{(x-\mu )^{3/2}}}\cdot \exp \left(-{\frac {\gamma }{2(x-\mu )}}\right),\quad x>\mu }$., mit den beiden Parametern ${\displaystyle \gamma >0,\,\mu \in \mathbb {R} }$.

• ${\displaystyle \mu }$ ist ein Lageparameter und definiert die Position auf der ${\displaystyle x}$-Achse;
• ${\displaystyle \gamma }$ ist ein Skalenparameter (Stauchung für ${\displaystyle \gamma <1}$; Streckung für ${\displaystyle \gamma >1}$).

Standard-Lévy-Verteilung

Die Standard-Lévy-Verteilung ist die Lévy-Verteilung mit den Parameterwerten ${\displaystyle \gamma =1,\mu =0}$; ihre Dichtefunktion lautet damit:

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi \cdot x^{3}}}}\cdot e^{-{\frac {1}{2x}}},\quad x>0}$.

Eigenschaften

Die Standard-Lévy-Verteilung gehört (wie d​ie Normalverteilung u​nd die Cauchy-Verteilung) z​ur übergeordneten Familie d​er alpha-stabilen Verteilungen, d. h., s​ie erfüllt d​ie Bedingung:

${\displaystyle (X_{1}+X_{2}+\dotsb +X_{n})\sim n^{1/\alpha }X}$

(hier mit ${\displaystyle \alpha =1/2}$) für alle unabhängigen Standard-Lévy-verteilten Zufallsgrößen ${\displaystyle X_{1},X_{2},\ldots ,X_{n},X}$. Da die Theorie der ${\displaystyle \alpha }$-stabilen Verteilungen maßgeblich von Lévy mitgestaltet wurde, spricht man, um Verwechslungen vorzubeugen, auch oft von der eigentlichen Lévy-Verteilung.

Momente

Die Lévy-Verteilung besitzt keinen endlichen Erwartungswert, denn es gilt ${\displaystyle \operatorname {E} (|X|)=\infty }$. Die Lévy-Verteilung gehört somit zu den Verteilungen mit schweren Rändern, die vor allem dazu verwendet werden, extreme Ereignisse (z. B. einen Börsencrash in der Finanzmathematik) zu modellieren.

Anwendung

Mit d​er Lévy-Verteilung lassen s​ich verschiedene Phänomene insbesondere i​n der Natur beschreiben:

• Brownsche Molekularbewegung[1]
• Verlauf von Börsenkursen[1]
• Umpolung des Erdmagnetfeldes[2]

Einzelnachweise

1. Applebaum, D.: Lectures on Lévy processes and Stochastic calculus, Braunschweig; Lecture 2: Lévy processes (PDF; 282 kB) University of Sheffield. S. 37–53. 22. Juli 2010. Abgerufen am 13. Juni 2014.
2. Belle Dumé: Geomagnetic flip may not be random after all. In: physicsworld.com. 21. März 2006. Abgerufen am 13. Juni 2014.