Quaternion

Die Quaternionen (Singular: die Quaternion, von lateinisch quaternio, -ionis f. „Vierheit“) sind ein Zahlenbereich, der den Zahlenbereich der reellen Zahlen erweitert – ähnlich den komplexen Zahlen und über diese hinaus. Beschrieben (und systematisch fortentwickelt) wurden sie ab 1843 von Sir William Rowan Hamilton;[1] sie werden deshalb auch hamiltonsche Quaternionen oder Hamilton-Zahlen genannt. Olinde Rodrigues entdeckte sie bereits 1840 unabhängig von Hamilton.[2] Trotzdem wird die Menge der Quaternionen meistens mit ${\displaystyle \mathbb {H} }$ bezeichnet.

ℍ

Die Quaternionen bilden einen Schiefkörper (oder Divisionsring), bei dem die Multiplikation auch von der Reihenfolge der Faktoren abhängt, also nicht kommutativ ist. Das heißt, es gibt Quaternionen ${\displaystyle x}$ und ${\displaystyle y}$, bei denen

${\displaystyle xy\;\;\neq \;\;yx}$

ist. Einige aus dem Reellen bekannte Rechenregeln gelten deshalb für Quaternionen nicht, jedoch gelten Assoziativ- und Distributivgesetz sowie multiplikative Invertierbarkeit, d. h. die Existenz des Inversen ${\displaystyle x^{-1}}$ zu jedem ${\displaystyle x\neq 0}$.

Die Quaternionen w​aren der e​rste derartige Gegenstand i​n der Geschichte d​er Mathematik.[3]

Quaternionen erlauben i​n vielen Fällen e​ine rechnerisch elegante Beschreibung d​es dreidimensionalen euklidischen Raumes u​nd anderer Räume, insbesondere i​m Kontext v​on Drehungen. Daher verwendet m​an sie u​nter anderem i​n Berechnungs- u​nd Darstellungsalgorithmen für Simulationen s​owie zur Auswertung kristallographischer Texturen.[4] Sie s​ind aber a​uch als eigenständiges mathematisches Objekt v​on Interesse u​nd dienen s​o zum Beispiel i​m Beweis d​es Vier-Quadrate-Satzes.

Konstruktion

Die Quaternionen entstehen aus den reellen Zahlen durch Hinzufügen (Adjunktion) dreier neuer Zahlen, denen in Anlehnung an die komplex-imaginäre Einheit die Namen ${\displaystyle \mathrm {i} }$, ${\displaystyle \mathrm {j} }$ und ${\displaystyle \mathrm {k} }$ gegeben werden. So ergibt sich ein vierdimensionales Zahlensystem (mathematisch: ein Vektorraum) mit einem Realteil, der aus einer reellen Komponente besteht, und einem Imaginärteil aus drei Komponenten, der auch Vektorteil genannt wird.

Jede Quaternion lässt s​ich eindeutig i​n der Form

${\displaystyle x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$

mit reellen Zahlen ${\displaystyle x_{0}}$, ${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$, ${\displaystyle x_{3}}$ schreiben. Damit bilden die Elemente ${\displaystyle 1,\mathrm {i} ,\mathrm {j} ,\mathrm {k} }$ eine Basis, die Standardbasis der Quaternionen über ${\displaystyle \mathbb {R} }$. Die Addition ist komponentenweise und wird vom Vektorraum geerbt. Multiplikativ werden die neuen Zahlen ${\displaystyle \mathrm {i} }$, ${\displaystyle \mathrm {j} }$, ${\displaystyle \mathrm {k} }$ gemäß den Hamilton-Regeln

${\displaystyle \mathrm {i} ^{2}=\mathrm {j} ^{2}=\mathrm {k} ^{2}=\mathrm {i} \mathrm {j} \mathrm {k} =-1}$

verknüpft. Die Skalarmultiplikation ${\displaystyle \mathbb {R} \times \mathbb {H} \to \mathbb {H} \,}$, die ebenfalls vom Vektorraum geerbt wird[5] und bei der die Skalare als mit jedem Element vertauschbar angesehen werden, zusammen mit der Addition, dem Rechtsdistributivgesetz und den Hamilton-Regeln erlauben es, die Multiplikation von der Basis auf alle Quaternionen zu erweitern. Da so auch jeder Skalar ${\displaystyle \lambda \in \mathbb {R} }$ als ${\displaystyle \lambda +0\mathrm {i} +0\mathrm {j} +0\mathrm {k} }$ in ${\displaystyle \mathbb {H} }$ eingebettet wird, kann ${\displaystyle \mathbb {R} }$ als Unterring von ${\displaystyle \mathbb {H} }$ aufgefasst werden.

Die so definierte Multiplikation ist assoziativ, erfüllt die beiden Distributivgesetze[6] und macht so die Quaternionen zu einem Ring. Sie ist allerdings nicht kommutativ, d. h. für zwei Quaternionen ${\displaystyle x}$ und ${\displaystyle y}$ sind die beiden Produkte ${\displaystyle xy}$ und ${\displaystyle yx}$ im Allgemeinen verschieden (s. u.). Das Zentrum von ${\displaystyle \mathbb {H} ^{\times }}$, also die Menge derjenigen Elemente der multiplikativen Gruppe von ${\displaystyle \mathbb {H} }$, die mit allen Elementen kommutieren, ist ${\displaystyle \mathbb {R} ^{\times }}$.

Die Quaternionen bilden einen Schiefkörper (Divisionsring), da es zu jeder Quaternion ${\displaystyle x\neq 0}$ eine inverse Quaternion ${\displaystyle x^{-1}}$ gibt mit

${\displaystyle xx^{-1}=x^{-1}x=1}$ .

Wegen der fehlenden Kommutativität werden Notationen mit Bruchstrich, wie z. B. ${\displaystyle {\tfrac {y}{x}}}$, vermieden.

Des Weiteren sind die Quaternionen eine vierdimensionale Divisionsalgebra über ${\displaystyle \mathbb {R} }$ – und bis auf Isomorphie die einzige.

Schreibweise

Im weiteren Text werden folgende Schreibweisen benutzt:

Ist ${\displaystyle x}$ eine Quaternion, dann werden ihre reellen Komponenten mit ${\displaystyle x_{0},x_{1},x_{2},x_{3}}$ bezeichnet, und diese sind der Basis ${\displaystyle 1,\mathrm {i} ,\mathrm {j} ,\mathrm {k} }$ folgendermaßen zugeordnet

${\displaystyle x=x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} .}$

Gelegentlich wird eine vektorielle Schreibweise benötigt. Dabei werden bspw. die Komponenten ${\displaystyle (x_{1},x_{2},x_{3})}$ zu einem 3-dimensionalen Vektor ${\displaystyle {\vec {x}}}$ zusammengefasst, so dass man ${\displaystyle x}$ mit dem 4-dimensionalen Vektor ${\displaystyle (x_{0},{\vec {x}})=(x_{0},x_{1},x_{2},x_{3})}$ identifizieren kann.[7]

Analoge Abmachungen sollen für andere Buchstaben wie ${\displaystyle y}$ etc. gelten.

In mancher älteren Literatur wurden Quaternionen mit großen Frakturbuchstaben und die imaginären Einheiten als Einheitsvektoren mit kleinen ${\displaystyle {\mathfrak {e}}_{n}}$ in Fraktur bezeichnet, z. B. so:

${\displaystyle {\mathfrak {X}}=x_{0}+{\mathfrak {e}}_{1}x_{1}+{\mathfrak {e}}_{2}x_{2}+{\mathfrak {e}}_{3}x_{3}=\sum _{j=0}^{3}{\mathfrak {e}}_{j}x_{j}}$

mit ${\displaystyle {\mathfrak {e}}_{0}=1}$ .

Komplexe Zahlen tragen meist den Namen ${\displaystyle z}$ und haben die reellen Komponenten ${\displaystyle \xi ,\eta }$.

Grundrechenarten

Die Konstruktion der Quaternionen ist der der komplexen Zahlen analog, allerdings wird nicht nur eine neue Zahl hinzugefügt, sondern derer drei, die mit ${\displaystyle \mathrm {i} }$, ${\displaystyle \mathrm {j} }$ und ${\displaystyle \mathrm {k} }$ bezeichnet werden.

Die Linearkombinationen

${\displaystyle x_{0}\mathrm {1} +x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$

über der Basis ${\displaystyle \{\mathrm {1} ,\mathrm {i} ,\mathrm {j} ,\mathrm {k} \}}$ spannen mit reellen Komponenten ${\displaystyle x_{i}}$ den 4-dimensionalen Vektorraum der Quaternionen ${\displaystyle \mathbb {H} }$ auf. Als Vektorraum ist ${\displaystyle \mathbb {H} }$ isomorph zu ${\displaystyle \mathbb {R} ^{4}}$. Das Basiselement ${\displaystyle \mathrm {1} }$, das die reellen Zahlen injektiv einbettet (und zugleich das neutrale Element der Multiplikation darstellt), wird in der Linearkombination meist weggelassen. Die Addition und Subtraktion geschieht komponentenweise wie in jedem Vektorraum.

Vom Vektorraum wird auch die Skalarmultiplikation übernommen, also die linke und rechte Multiplikation mit einer reellen Zahl, die distributiv zu jeder Komponente multipliziert wird. Diese Skalarmultiplikation ist eine Einschränkung der Hamilton-Multiplikation, die auf ganz ${\displaystyle \mathbb {H} }$ definiert ist. Die Hamilton-Multiplikation der Basiselemente untereinander oder etwas umfassender innerhalb der Menge

${\displaystyle \mathrm {Q} _{8}:=\{\mathrm {1} ,\mathrm {i} ,\mathrm {j} ,\mathrm {k} ,-\mathrm {1} ,-\mathrm {i} ,-\mathrm {j} ,-\mathrm {k} \}}$

geschieht n​ach den Hamilton-Regeln

${\displaystyle \mathrm {i} ^{2}=\mathrm {j} ^{2}=\mathrm {k} ^{2}=-1}$	${\displaystyle (1)}$
${\displaystyle \mathrm {i} \mathrm {j} =+\mathrm {k} ,\quad \mathrm {j} \mathrm {k} =+\mathrm {i} ,\quad \mathrm {k} \mathrm {i} =+\mathrm {j} }$	${\displaystyle (2)}$
${\displaystyle \mathrm {j} \mathrm {i} =-\mathrm {k} ,\quad \mathrm {k} \mathrm {j} =-\mathrm {i} ,\quad \mathrm {i} \mathrm {k} =-\mathrm {j} }$	${\displaystyle ({\bar {2}})}$.

Diese Regeln zusammen mit der Vertauschbarkeit von ${\displaystyle \pm 1}$ mit jedem anderen Element geben eine vollständige Tafel für eine Verknüpfung vor, die sich als assoziativ erweist und ${\displaystyle \mathrm {Q} _{8}}$ zu einer Gruppe macht – der Quaternionengruppe.

Unter Voraussetzung der Regel ${\displaystyle (1)}$ (und der Gruppenaxiome) ist die Kombination aus ${\displaystyle (2)}$ und ${\displaystyle ({\bar {2}})}$, in der das zyklische und antizyklische Verhalten der drei nicht-reellen Quaternionen-Einheiten zum Ausdruck kommt, ersetzbar durch die Einzelregel

${\displaystyle \mathrm {i} \mathrm {j} \mathrm {k} =-1}$

${\displaystyle (3)}$.

Diese Einzelregel ${\displaystyle (3)}$ könnte auch durch jede der fünf alternativen Einzelregeln ${\displaystyle \mathrm {j} \mathrm {k} \mathrm {i} =-1}$, ${\displaystyle \mathrm {k} \mathrm {i} \mathrm {j} =-1}$, ${\displaystyle \mathrm {k} \mathrm {j} \mathrm {i} =1}$, ${\displaystyle \mathrm {j} \mathrm {i} \mathrm {k} =1}$ oder ${\displaystyle \mathrm {i} \mathrm {k} \mathrm {j} =1}$ ersetzt werden.

Mithilfe dieser Ersetzungsregeln, dem Assoziativgesetz und (linkem wie rechtem) Distributivgesetz lässt sich die Multiplikation auf ganz ${\displaystyle \mathbb {H} }$ fortsetzen. Die ${\displaystyle \mathrm {i} ,\mathrm {j} ,\mathrm {k} }$ kann man wie anti-kommutierende Variablen behandeln. Treten Produkte von zweien von ihnen auf, so darf man sie nach den Hamilton-Regeln ersetzen.

Die ausgearbeiteten Formeln für d​ie 2 Verknüpfungen v​on zwei Quaternionen

${\displaystyle x=x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$   und   ${\displaystyle y=y_{0}+y_{1}\mathrm {i} +y_{2}\mathrm {j} +y_{3}\mathrm {k} }$

lauten

${\displaystyle x+y}$	${\displaystyle =(x_{0}+y_{0})+(x_{1}+y_{1})\mathrm {i} +(x_{2}+y_{2})\mathrm {j} +(x_{3}+y_{3})\mathrm {k} }$		(Addition)
${\displaystyle x\;y}$	${\displaystyle =(x_{0}y_{0}-x_{1}y_{1}-x_{2}y_{2}-x_{3}y_{3})}$
	${\displaystyle {}+(x_{0}y_{1}+x_{1}y_{0}{\color {Red}\;+\;x_{2}y_{3}}{\color {red}\;-\;x_{3}y_{2}})\mathrm {i} }$
	${\displaystyle {}+(x_{0}y_{2}{\color {red}\;-\;x_{1}y_{3}}+x_{2}y_{0}{\color {Red}\;+\;x_{3}y_{1}})\mathrm {j} }$
	${\displaystyle {}+(x_{0}y_{3}{\color {Red}\;+\;x_{1}y_{2}}{\color {red}\;-\;x_{2}y_{1}}+x_{3}y_{0})\mathrm {k} }$		(Multiplikation)

Hiermit s​ind die für e​inen Ring erforderlichen 2 Verknüpfungen definiert. Es i​st leicht nachgerechnet, d​ass alle Ring-Axiome erfüllt sind.

Das additive Inverse i​st (wie i​n jedem Vektorraum) d​as Produkt m​it dem Skalar −1. Die Subtraktion i​st die Addition dieses Inversen.

Die für e​inen Schiefkörper erforderliche Division m​uss wegen d​er fehlenden Kommutativität d​urch eine Multiplikation m​it dem (multiplikativen) Inversen ersetzt werden (siehe Inverses u​nd Division).[8]

Gegenring

Ist ${\displaystyle \mathbb {H} }$ ein nicht-kommutativer Ring, dann lässt sich mit der Multiplikation

${\displaystyle x\circ y\;:=y\cdot x}$

ein anderer Ring, der Gegenring genannte Ring ${\displaystyle \mathbb {H} ^{op}:=(\mathbb {R} ^{4},+,\circ )}$, erzeugen. Man überlegt leicht, dass alle Ringgesetze, das heißt Assoziativgesetz sowie beide Distributivgesetze, aus den ursprünglichen Gesetzen folgen. In diesem Ring gelten (fast) alle im § Grundrechenarten aufgeschriebenen Rechenregeln bis auf die Multiplikation, bei der die Vorzeichen der dort in roter Schrift gehaltenen Terme (welches genau diejenigen sind, in denen eine Komponente mit Index 0 nicht vorkommt) invertiert sind. Ferner gilt die Kurzform

${\displaystyle \mathrm {i} \circ \mathrm {j} \circ \mathrm {k} =+1}$ .

Übrigens h​at Gauß l​aut Lam^{:Eq. (1.4)} d​ie Quaternionenmultiplikation i​m Jahr 1819 g​enau so definiert.

Des Weiteren ist die Orientierung des Dreibeins ${\displaystyle (\mathrm {i} ,\mathrm {j} ,\mathrm {k} )}$ in ${\displaystyle \mathbb {H} ^{op}}$ gespiegelt. Die Identität auf der Grundmenge ${\displaystyle \mathbb {R} ^{4}}$ ist ein Antiisomorphismus und die Konjugation ein Isomorphismus

${\displaystyle \mathbb {H}$ :=(\mathbb {R} ^{4},+,\cdot )\quad \to \quad \mathbb {H} ^{op}:=(\mathbb {R} ^{4},+,\circ )} .

Die Nichtkommutativität ist gleichbedeutend mit der Verschiedenheit von ${\displaystyle \mathbb {H} }$ und ${\displaystyle \mathbb {H} ^{op}}$. Da beide Ringe die Ringaxiome der Quaternionen erfüllen, muss dieses Axiomensystem „unvollständig“ sein im Sinne Hölders. In diesem Sinn vollständig sind die Axiomensysteme der rationalen, reellen oder komplexen Zahlen.

Grundlegende Begriffe

Skalarteil und Vektorteil

Aufgrund der besonderen Stellung der Komponente ${\displaystyle x_{0}}$ einer Quaternion

${\displaystyle x=x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$

bezeichnet m​an sie – w​ie bei d​en komplexen Zahlen – a​ls Realteil o​der Skalarteil

${\displaystyle \operatorname {Re} \,x:=x_{0}}$ ,

während die Komponenten ${\displaystyle x_{1},x_{2},x_{3}}$ zusammen den Imaginärteil oder Vektorteil

${\displaystyle \operatorname {Im} \,x:=x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$

bilden. Häufig identifiziert man den Vektorteil auch mit dem Vektor ${\displaystyle {\vec {x}}:=(x_{1},x_{2},x_{3})\in \mathbb {R} ^{3}}$.

Konjugation

Zu j​eder Quaternion

${\displaystyle x=x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$

ist d​ie konjugierte Quaternion definiert als

${\displaystyle {\bar {x}}:=x_{0}-x_{1}\mathrm {i} -x_{2}\mathrm {j} -x_{3}\mathrm {k} }$ .

Da h​ier der Imaginärteil m​it seinen Einheitsvektoren verknüpft bleibt u​nd der Realteil a​ls reelle Zahl eindeutig i​n die Quaternionen einzubetten ist, ergeben s​ich die einfachen Beziehungen

${\displaystyle x=\operatorname {Re} \,x+\operatorname {Im} \,x}$

und

${\displaystyle {\bar {x}}=\operatorname {Re} \,x-\operatorname {Im} \,x}$ ,

aus d​enen sich unmittelbar

${\displaystyle \operatorname {Re} \,x={\frac {1}{2}}(x+{\bar {x}})}$

und

${\displaystyle \operatorname {Im} \,x={\frac {1}{2}}(x-{\bar {x}})}$

ausrechnet.[9]

Ist e​ine Quaternion gleich i​hrer Konjugierten, s​o ist s​ie reell, d. h. d​er Vektorteil i​st null. Ist e​ine Quaternion gleich d​em Negativen i​hrer Konjugierten, s​o ist s​ie eine reine Quaternion, d. h. d​er Skalarteil i​st null.

Weitere wichtige Eigenschaften d​er Konjugation sind:

${\displaystyle {\overline {({\bar {x}})}}=x}$	Die Konjugation i​st eine Involution.
${\displaystyle {\overline {x+y}}={\bar {x}}+{\bar {y}}}$ und ${\displaystyle {\overline {\lambda x}}=\lambda {\bar {x}}}$ für reelle Zahlen ${\displaystyle \lambda }$	Die Konjugation ist ${\displaystyle \mathbb {R} }$-linear.
${\displaystyle {\overline {xy}}={\bar {y}}{\bar {x}}}$	Die Konjugation i​st ein involutiver Antiautomorphismus.
${\displaystyle {\overline {x}}=-{\tfrac {1}{2}}(x+\mathrm {i} \,x\,\mathrm {i} +\mathrm {j} \,x\,\mathrm {j} +\mathrm {k} x\mathrm {k} )}$	Die Konjugation lässt s​ich „mit arithmetischen Mitteln“ darstellen.[10]

Skalarprodukt

Das Skalarprodukt ${\displaystyle \langle {\cdot },{\cdot }\rangle \colon \mathbb {H} \times \mathbb {H} \to \mathbb {R} }$ zweier Quaternionen, aufgefasst als Vektoren im ${\displaystyle \mathbb {R} ^{4}}$, ist definiert durch

${\displaystyle \langle x,y\rangle$ :=x_{0}y_{0}+x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}}  .

Es gilt

${\displaystyle \langle x,y\rangle =\operatorname {Re} ({\bar {x}}y)=\operatorname {Re} (x{\bar {y}})={\frac {1}{2}}(x{\bar {y}}+y{\bar {x}})}$ .

Es i​st eine positiv definite symmetrische Bilinearform, über d​ie sich Norm u​nd Betrag definieren lassen u​nd mit d​er Winkel u​nd Orthogonalität bestimmt werden können.

Ferner k​ann man d​amit die einzelnen Komponenten e​iner Quaternion isolieren:

${\displaystyle x_{0}=\langle \mathrm {1} ,x\rangle ,\quad x_{1}=\langle \mathrm {i} ,x\rangle ,\quad x_{2}=\langle \mathrm {j} ,x\rangle ,\quad x_{3}=\langle \mathrm {k} ,x\rangle }$ .

Das aus der Physik weit verbreitete Vorgehen, das Skalarprodukt abkürzend wie eine Multiplikation mit dem Mittepunkt „${\displaystyle \cdot }$“ zu notieren, wird auch bei den Quaternionen häufig angewandt, wobei hier die Verwechslungsgefahr zwischen Quaternionenmultiplikation und Skalarprodukt hoch ist.

Im Folgenden verwenden w​ir folgende Konvention:

• Das Quaternionenprodukt wird stets ohne Benutzung des Mittepunkts durch Aneinanderreihung der Faktoren notiert.
• Das Skalarprodukt, und zwar sowohl das 4- wie das 3-dimensionale, wird in Multiplikationsschreibweise mit dem Mittepunkt „${\displaystyle \cdot }$“ notiert.

Kreuzprodukt

Das Kreuzprodukt zweier Quaternionen ${\displaystyle x,y}$ ist das Kreuzprodukt (Vektorprodukt) ihrer Vektorteile und bis auf den Faktor 2 ihr Kommutator. Ist ${\displaystyle x=:(x_{0},{\vec {x}})}$ und ${\displaystyle y=:(y_{0},{\vec {y}})}$, so ist

${\displaystyle {\begin{aligned}x\times y&:={\vec {x}}\times {\vec {y}}\\&\;={\tfrac {1}{2}}(xy-yx)\\&\;=(x_{2}y_{3}-x_{3}y_{2})\mathrm {i} +(x_{3}y_{1}-x_{1}y_{3})\mathrm {j} +(x_{1}y_{2}-x_{2}y_{1})\mathrm {k} \;.\end{aligned}}}$

Quaternionenmultiplikation als Skalar- und Kreuzprodukt

Identifiziert m​an Quaternionen

${\displaystyle x=x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$

und

${\displaystyle y=y_{0}+y_{1}\mathrm {i} +y_{2}\mathrm {j} +y_{3}\mathrm {k} }$

mit Paaren aus einem Skalar ${\displaystyle \in \mathbb {R} }$ und einem Vektor ${\displaystyle \in \mathbb {R} ^{3}}$

${\displaystyle x=(x_{0},{\vec {x}})}$   mit   ${\displaystyle {\vec {x}}:=(x_{1},x_{2},x_{3})}$

bzw.

${\displaystyle y=(y_{0},{\vec {y}})}$   mit   ${\displaystyle {\vec {y}}:=(y_{1},y_{2},y_{3})}$ ,

so lässt s​ich die Multiplikation mithilfe d​es (dreidimensionalen) Skalarprodukts u​nd Kreuzprodukts beschreiben:

${\displaystyle xy=(x_{0},{\vec {x}})(y_{0},{\vec {y}})={\Big (}x_{0}y_{0}-{\vec {x}}\cdot {\vec {y}},\quad x_{0}{\vec {y}}+{\vec {x}}y_{0}+{\vec {x}}\times {\vec {y}}{\Big )}}$ .

Zwei Quaternionen sind demnach genau dann miteinander vertauschbar, wenn ihr Kreuzprodukt 0 ist, wenn also ihre Vektorteile als reelle Vektoren linear abhängig sind (s. a. Einbettung der komplexen Zahlen).

Norm und Betrag

Das Skalarprodukt einer Quaternion ${\displaystyle x}$ mit sich selbst, welches gleich dem Quaternionenprodukt mit der Konjugierten ist, wird Norm genannt:

${\displaystyle \operatorname {Norm} (x):=x\cdot x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=x{\bar {x}}={\bar {x}}x}$ [11]

Insbesondere i​st dieser Wert r​eell und nichtnegativ.

Die Quadratwurzel hieraus

${\displaystyle {\sqrt {{x_{0}}^{2}+{x_{1}}^{2}+{x_{2}}^{2}+{x_{3}}^{2}}}=:|x|}$

wird Betrag oder Länge der Quaternion ${\displaystyle x}$ genannt und stimmt überein mit Betrag oder euklidischer Länge des Vektors ${\displaystyle (x_{0},x_{1},x_{2},x_{3})}$. Er erfüllt die wichtige Eigenschaft

${\displaystyle |xy|=|x|\;|y|}$ ,

die Multiplikativität des Betrags. Mit dem Betrag werden die Quaternionen zu einer reellen Banachalgebra.

Inverses und Division

Bei e​iner nicht-kommutativen Multiplikation m​uss man d​ie Gleichungen

${\displaystyle xb=a}$

und

${\displaystyle by=a}$

unterscheiden. Wenn das Inverse ${\displaystyle b^{-1}}$ existiert, dann sind

${\displaystyle x=ab^{-1}}$

bzw.

${\displaystyle y=b^{-1}a}$

respektive Lösungen, die nur dann übereinstimmen, wenn ${\displaystyle b}$ und ${\displaystyle a}$ kommutieren, insbesondere wenn der Divisor ${\displaystyle b}$ reell ist. In solch einem Fall kann die Schreibweise ${\displaystyle {\tfrac {a}{b}}}$ verwendet werden – bei allgemeinen Divisionen wäre sie nicht eindeutig.

Wenn zusätzlich ${\displaystyle c^{-1}}$ existiert, gilt die Formel

${\displaystyle b^{-1}c^{-1}=(cb)^{-1}}$,

denn

${\displaystyle b^{-1}c^{-1}cb=1}$      und     ${\displaystyle (cb)^{-1}cb=1}$ .

Für

${\displaystyle x=x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} \neq 0}$

ist d​ie Norm

${\displaystyle \operatorname {Norm} (x)=x{\bar {x}}={\bar {x}}x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}>0}$

reell u​nd positiv. Die Quaternion

${\displaystyle x^{-1}:={\frac {\bar {x}}{x{\bar {x}}}}}$

erfüllt d​ann die Bedingungen d​es Rechts-

${\displaystyle xx^{-1}=x{\frac {\bar {x}}{x{\bar {x}}}}=1}$

und d​es Links-Inversen

${\displaystyle x^{-1}x={\frac {\bar {x}}{{\bar {x}}x}}x=1}$

und kann deshalb als das Inverse schlechthin von ${\displaystyle x}$ bezeichnet werden.

Reine Quaternion

Eine Quaternion, d​eren Vektorteil 0 ist, w​ird mit d​er ihrem Skalarteil entsprechenden reellen Zahl identifiziert.

Eine Quaternion, deren Realteil 0 ist (äquivalent: deren Quadrat reell und nichtpositiv ist), nennt man rein, rein imaginär oder vektoriell. Die Menge der reinen Quaternionen wird als ${\displaystyle \mathbb {H} _{\text{pure}}}$ oder ${\displaystyle \operatorname {Im} \,\mathbb {H} }$ notiert. Sie ist ein dreidimensionaler reeller Vektorraum mit Basis ${\displaystyle \{\mathrm {i} ,\mathrm {j} ,\mathrm {k} \}}$. Für reine Quaternionen nimmt die Multiplikation eine besonders einfache Form an:

${\displaystyle (0,{\vec {x}})(0,{\vec {y}})\;=\;{\Big (}{-{\vec {x}}\cdot {\vec {y}}},\,{\vec {x}}\times {\vec {y}}{\Big )}}$ .

Einheitsquaternion

Eine Einheitsquaternion (auch: normierte Quaternion, Quaternion der Länge 1) i​st eine Quaternion, d​eren Betrag gleich 1 ist. Für s​ie gilt (analog z​u den komplexen Zahlen)

${\displaystyle |x|=1\iff x{\bar {x}}=1\iff {\bar {x}}=x^{-1}}$.

Für eine beliebige Quaternion ${\displaystyle x\neq 0}$ ist

${\displaystyle {\frac {x}{|x|}}={\frac {x_{0}}{|x|}}+{\frac {x_{1}}{|x|}}\mathrm {i} +{\frac {x_{2}}{|x|}}\mathrm {j} +{\frac {x_{3}}{|x|}}\mathrm {k} }$

eine Einheitsquaternion, die man manchmal auch als das Signum oder den Versor von ${\displaystyle x}$ bezeichnet.

Das Produkt zweier Einheitsquaternionen u​nd die Inverse e​iner Einheitsquaternion s​ind wieder Einheitsquaternionen. Die Einheitsquaternionen bilden a​lso eine Gruppe.

Geometrisch kann man die Menge der Einheitsquaternionen als die Einheits-3-Sphäre ${\displaystyle \mathbb {S} ^{3}}$ im vierdimensionalen euklidischen Raum und damit als Lie-Gruppe interpretieren, mit dem Raum der reinen Quaternionen als zugehöriger Lie-Algebra. Die Darstellung als komplexe Matrizen verdeutlicht die umkehrbar eindeutige Entsprechung der Einheitsquaternionen mit der speziellen unitären Gruppe ${\displaystyle \mathrm {SU} (2)}$.

Die einzigen reellen Einheitsquaternionen sind ${\displaystyle \pm 1}$. Sie machen auch das Zentrum von ${\displaystyle \mathbb {S} ^{3}}$ aus.

Reine Einheitsquaternion

Einheitsquaternionen, die auch reine Quaternionen sind, lassen sich als diejenigen Quaternionen charakterisieren, deren Quadrate ${\displaystyle -1}$ ergeben:

${\displaystyle \epsilon _{0}=0\;\land \;{\epsilon _{1}}^{2}+{\epsilon _{2}}^{2}+{\epsilon _{3}}^{2}=1\qquad \iff \qquad \epsilon ^{2}=-1}$.[12]

Sie liegen in der Äquatorhyperebene der 3-Sphäre ${\displaystyle \mathbb {S} ^{3}}$ und machen die Einheits-2-Sphäre ${\displaystyle \mathbb {S} ^{2}}$ des dreidimensionalen Raums ${\displaystyle \operatorname {Im} \,\mathbb {H} }$ aus.

Einbettung der komplexen Zahlen

Jede Quaternion ${\displaystyle \epsilon }$ mit Quadrat ${\displaystyle -1}$ definiert einen Einbettungsisomorphismus ${\displaystyle \iota _{\epsilon }}$ der komplexen Zahlen in die Quaternionen

${\displaystyle {\begin{array}{rccc}\iota _{\epsilon }\colon &\mathbb {C} &\to &\mathbb {H} \\&u+v\mathrm {i} _{\mathbb {C} }&\mapsto &u+v\epsilon \end{array}}}$

mit ${\displaystyle u,v\in \mathbb {R} }$ und ${\displaystyle \mathrm {i} _{\mathbb {C} }}$ als imaginärer Einheit der komplexen Zahlen. Dabei sind die Bildmengen der ${\displaystyle \epsilon }$ und ${\displaystyle {\bar {\epsilon }}}$ entsprechenden Einbettungen identisch: ${\displaystyle \iota _{\epsilon }(\mathbb {C} )=\iota _{\overline {\epsilon }}(\mathbb {C} )}$.

Eine jede solche Quaternion darf ${\displaystyle \mathrm {i} }$ genannt werden, eine senkrechte dazu ${\displaystyle \mathrm {j} }$ und ihr Produkt ${\displaystyle \mathrm {k} }$.[13]^{:Seite 40.} [14] Jede nicht-reelle Quaternion liegt in genau einer solchen Einbettung von ${\displaystyle \mathbb {C} }$ . Zwei Quaternionen sind genau dann vertauschbar, wenn es eine gemeinsame Einbettung gibt.

Zwei verschiedene Bilder h​aben die reelle Achse z​um Durchschnitt.

So betrachtet, s​ind die Quaternionen e​ine Vereinigung komplexer Ebenen.

Polardarstellung

Jede Einheitsquaternion ${\displaystyle x^{\circ }=x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} \;\neq \;\pm 1}$ kann auf eindeutige Weise in der Form

${\displaystyle x^{\circ }=\cos \phi +\epsilon \,\sin \phi }$

mit dem Polarwinkel[15] von ${\displaystyle x^{\circ }}$

${\displaystyle \phi$ :=\arccos(x_{0})=\arccos(\operatorname {Re} x^{\circ })\in {]0,\pi [}}

und der reinen Einheitsquaternion

${\displaystyle \epsilon$ :={\frac {x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }{\sqrt {1-x_{0}^{2}}}}={\frac {x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }{\sin \phi }}={\frac {\operatorname {Im} x^{\circ }}{|\operatorname {Im} x^{\circ }|}}={\frac {{\vec {x}}^{\circ }}{|{\vec {x}}^{\circ }|}}}

dargestellt werden.

Mit der verallgemeinerten Exponentialfunktion lässt sich dies wegen ${\displaystyle \epsilon ^{2}=-1\ }$ auch schreiben als

${\displaystyle x^{\circ }=\exp(\epsilon \phi )}$

mit der reinen Quaternion ${\displaystyle \epsilon \phi =:x^{\prime }\in \operatorname {Im} \,\mathbb {H} }$. Will man also eine reine Quaternion ${\displaystyle x^{\prime }\neq 0}$ exponentiieren, so ist ihr Betrag ${\displaystyle \phi =|x^{\prime }|}$ und die reine Einheitsquaternion ${\displaystyle \epsilon =x^{\prime }/\phi }$ zu bilden, und es ergibt sich die Einheitsquaternion

${\displaystyle \exp x^{\prime }=\cos \phi +\epsilon \,\sin \phi }$.

Der Fall   ${\displaystyle \exp 0=1}$   lässt sich stetig ergänzen. Damit ist die Exponentialabbildung ${\displaystyle \exp \colon \operatorname {Im} \,\mathbb {H} \to \mathbb {S} ^{3}}$ surjektiv. Nun ist ${\displaystyle \exp x^{\prime }=-1}$ für alle ${\displaystyle x^{\prime }\in \operatorname {Im} \,\mathbb {H} }$ mit ${\displaystyle |x^{\prime }|=\pi }$, und das sind unendlich viele. Gleichwohl ist die Einschränkung ${\displaystyle \exp \colon \{x^{\prime }\in \operatorname {Im} \,\mathbb {H} \land |x^{\prime }|<\pi \}\;\to \;\mathbb {S} ^{3}\setminus \{-1\}}$ bijektiv. Sie ist stetig, wegen der Nicht-Kommutativität der Multiplikation aber kein Homomorphismus[16].

Allgemein lässt sich jede nicht-reelle Quaternion eindeutig in der Form

${\displaystyle x=|x|\;(\cos \phi +\epsilon \,\sin \phi )}$

mit dem Polarwinkel von ${\displaystyle x}$

${\displaystyle \phi =\arccos \left({\frac {\operatorname {Re} x}{|x|}}\right)\in {]0,\pi [}}$

und der reinen Einheitsquaternion (der reinen und normierten Quaternion von ${\displaystyle x}$)

${\displaystyle \epsilon ={\frac {\operatorname {Im} x}{\sqrt {|x|^{2}-(\operatorname {Re} x)^{2}}}}={\frac {\operatorname {Im} x}{|x|\,\sin \phi }}={\frac {\vec {x}}{|{\vec {x}}|}}}$

schreiben. Durch die Festlegung ${\displaystyle \phi \in {]0,\pi [}}$ ist ${\displaystyle \sin \phi >0}$, so dass ${\displaystyle \epsilon }$ in dieselbe Richtung wie der Vektorteil ${\displaystyle \operatorname {Im} x}$ zeigt.

Jede n​icht reell-negative Quaternion schreibt s​ich eindeutig als

${\displaystyle x=|x|\exp x^{\prime }}$

mit einer reinen Quaternion ${\displaystyle x^{\prime }}$ mit   ${\displaystyle |x^{\prime }|<\pi }$.

Diese Darstellungen s​ind der Polarform komplexer Zahlen

${\displaystyle z=|z|(\cos \phi +\mathrm {i} _{\mathbb {C} }\sin \phi )=|z|\exp(\mathrm {i} _{\mathbb {C} }\phi )}$

(mit ${\displaystyle \mathrm {i} _{\mathbb {C} }}$ als imaginärer Einheit) analog. Für die Funktionalgleichung

${\displaystyle xy=|x|\;|y|\;\exp(x^{\prime }+y^{\prime })}$

müssen ${\displaystyle x,y}$ allerdings kommutieren.[16][17]

Funktionentheorie

Exponentialfunktion, Logarithmus

Das Exponential einer nicht-reellen Quaternion ${\displaystyle x}$ ist:

${\displaystyle \exp(x)=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}=\exp(\operatorname {Re} x)\left(\cos |{\vec {x}}|+{\frac {\vec {x}}{|{\vec {x}}|}}\sin |{\vec {x}}|\right)}$

mit ${\displaystyle {\vec {x}}:=\operatorname {Im} x}$ .

Der (natürliche) Logarithmus einer nicht-reellen Quaternion ${\displaystyle x}$ ist:

${\displaystyle \ln(x)=\ln |x|+{\frac {\vec {x}}{|{\vec {x}}|}}\arccos \left({\frac {\operatorname {Re} x}{|x|}}\right)}$ [18]

Für nicht-reelles ${\displaystyle x}$ sind sie Umkehrfunktionen voneinander

${\displaystyle \exp(\ln(x))=x}$

und, falls ${\displaystyle |{\vec {x}}|<\pi }$,

${\displaystyle \ln(\exp(x))=x}$ .

Für nicht-reelles, mit ${\displaystyle x}$ kommutierendes ${\displaystyle y}$ gelten die Funktionalgleichungen

${\displaystyle \exp(x+y)=\exp(x)\exp(y)}$

und

${\displaystyle \ln(x)+\ln(y)=\ln(xy)}$ ,

letzteres für ${\displaystyle x,y}$ mit hinreichend kleinem Imaginärteil.

Fortsetzungen komplexer Funktionen

Im kommutativen Diagramm müssen sich ${\displaystyle g_{\epsilon }}$ und ${\displaystyle g_{\zeta }}$ auf ${\displaystyle \iota _{\epsilon }\mathbb {C} \;\cap \;\iota _{\zeta }\mathbb {C} \;\subset \;\mathbb {H} }$ vertragen.

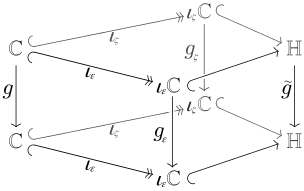
Da ${\displaystyle \mathbb {H} }$ als eine Vereinigung von Einbettungen komplexer Ebenen aufgefasst werden kann (s. Abschnitt #Einbettung der komplexen Zahlen), kann man versuchen, Funktionen ${\displaystyle g\colon \mathbb {C} \to \mathbb {C} }$[19] mithilfe der genannten Einbettungsisomorphismen ${\displaystyle \iota _{\epsilon }}$ vom Komplexen ins Quaternionische zu liften. Dabei ist zu fordern, dass die so gewonnenen Funktionen ${\displaystyle g_{\epsilon }\colon \iota _{\epsilon }(\mathbb {C} )\to \iota _{\epsilon }(\mathbb {C} )\subset \mathbb {H} }$ mit ${\displaystyle g_{\epsilon }(q):=\iota _{\epsilon }\circ g\circ {\iota _{\epsilon }}^{-1}(q)}$ bei Überschneidungen der Definitionsbereiche dasselbe Ergebnis liefern, so dass die vereinigte Funktion ${\displaystyle {\tilde {g}}}$ auf der Vereinigungsmenge ${\displaystyle \cup _{\epsilon }{\bigl (}\iota _{\epsilon }(\mathbb {C} ){\bigr )}=\mathbb {H} }$ vermöge ${\displaystyle \forall q\in \mathbb {H} \;\exists \epsilon :q\in \iota _{\epsilon }(\mathbb {C} )}$ als ${\displaystyle {\tilde {g}}(q):=g_{\epsilon }(q)}$ in wohldefinierter Weise gebildet werden kann.

Sei ${\displaystyle g(z)=u(\xi ,\eta )+v(\xi ,\eta )\ \mathrm {i} _{\mathbb {C} }}$ eine komplexwertige Funktion ${\displaystyle \mathbb {C} \to \mathbb {C} }$ einer komplexen Variablen ${\displaystyle z=\xi +\eta \,\mathrm {i} _{\mathbb {C} }}$ mit reellen ${\displaystyle \xi ,\eta }$ und reellen ${\displaystyle u(\xi ,\eta ),v(\xi ,\eta ).}$
Einbettbarkeit: ${\displaystyle g}$ ist genau dann einbettbar in die Quaternionen, wenn ${\displaystyle u}$ eine gerade und ${\displaystyle v}$ eine ungerade Funktion des jeweils zweiten Arguments ${\displaystyle \eta }$ ist.[20]

Beweis

Ist ${\displaystyle q}$ eine beliebige nicht-reelle Quaternion, dann ist ${\displaystyle \epsilon$ :=\operatorname {Im} q/|\operatorname {Im} q|} eine reine und normierte Quaternion mit ${\displaystyle \epsilon ^{2}=-1}$. Seien ferner ${\displaystyle \xi$ :=\operatorname {Re} q} und ${\displaystyle \eta$ :=|\operatorname {Im} q|} , die beide reell sind. Sowohl ${\displaystyle \iota _{\epsilon }}$ wie ${\displaystyle \iota _{\overline {\epsilon }}}$ ist ein Einbettungsisomorphismus für das Bild ${\displaystyle q}$. Im ersteren Fall ist ${\displaystyle z_{\epsilon }:=\xi +\eta \,\mathrm {i} _{\mathbb {C} }\in \mathbb {C} }$ das Urbild von ${\displaystyle q=\xi +\eta \,\epsilon }$, im zweiten Fall haben wir wegen ${\displaystyle q=\xi +\eta \,\epsilon =\xi -\eta \,{\bar {\epsilon }}}$ das Urbild ${\displaystyle z_{\overline {\epsilon }}:=\iota _{\overline {\epsilon }}^{-1}(\xi -\eta \,\epsilon )=\xi -\eta \,\mathrm {i} _{\mathbb {C} }}$; jeweils mit ${\displaystyle \mathrm {i} _{\mathbb {C} }}$ als der imaginären Einheit von ${\displaystyle \mathbb {C} }$. Die Urbilder sind verschieden, das Bild, das bei der zu bildenden Funktion ${\displaystyle {\tilde {g}}}$ als Argument fungieren soll, ist aber beidesmal ${\displaystyle q}$. Das „Liften“ wird durch die Einbettung der Funktionswerte als ${\displaystyle g_{\epsilon }(q):=\iota _{\epsilon }(g(z_{\epsilon }))=\iota _{\epsilon }(u(\xi ,+\eta )+v(\xi ,+\eta )\mathrm {i} _{\mathbb {C} })=u(\xi ,+\eta )+v(\xi ,+\eta )\epsilon }$ und ${\displaystyle g_{\overline {\epsilon }}(q):=\iota _{\overline {\epsilon }}(g(z_{\overline {\epsilon }}))=\iota _{\overline {\epsilon }}(u(\xi ,-\eta )+v(\xi ,-\eta )\mathrm {i} _{\mathbb {C} })=u(\xi ,-\eta )+v(\xi ,-\eta ){\bar {\epsilon }}}$ vervollständigt (s. Diagramm). Nun i​st nach Voraussetzung ${\displaystyle u(\xi ,+\eta )=u(\xi ,-\eta ),\quad v(\xi ,+\eta )=-v(\xi ,-\eta ),}$ so d​ass sich ${\displaystyle g_{\overline {\epsilon }}(q)=u(\xi ,-\eta )+v(\xi ,-\eta ){\bar {\epsilon }}=u(\xi ,-\eta )-v(\xi ,-\eta )\epsilon =u(\xi ,+\eta )+\ v(\xi ,+\eta )\epsilon =g_{\epsilon }(q)}$ ergibt und ${\displaystyle {\tilde {g}}(q)}$ nicht von der Wahl des Einbettungsisomorphismus abhängt. Die Bedingung ist auch notwendig. Denn lässt umgekehrt die Funktion ${\displaystyle g(\xi +\eta \,\mathrm {i} _{\mathbb {C} })=u(\xi ,\eta )+v(\xi ,\eta )\mathrm {i} _{\mathbb {C} }}$ eine Einbettung ${\displaystyle {\tilde {g}}\colon \mathbb {H} \to \mathbb {H} ;q\mapsto {\tilde {g}}(q)}$ in die Quaternionen zu, so gibt es zu jedem ${\displaystyle q\in \mathbb {H} }$ eine geeignete reine Einheitsquaternion ${\displaystyle \epsilon }$ und reelle ${\displaystyle \xi ,\eta }$ mit ${\displaystyle q=\xi \,+\,\eta \,\epsilon }$ und ${\displaystyle {\begin{array}{llll}{\tilde {g}}(q)&=g_{\epsilon }(\xi \,+\,\eta \,\epsilon )=g_{\epsilon }(\iota _{\epsilon }(\xi +\eta \,\mathrm {i} _{\mathbb {C} }))=\iota _{\epsilon }(g(\xi +\eta \,\mathrm {i} _{\mathbb {C} }))\\&=\iota _{\epsilon }(u(\xi ,+\eta )\,+\,v(\xi ,+\eta )\mathrm {i} _{\mathbb {C} })&=u(\xi ,+\eta )\,+\,v(\xi ,+\eta )\epsilon .\end{array}}}$ Bei der konjugierten Quaternion ${\displaystyle {\bar {\epsilon }}=-\epsilon }$ hat die Einbettung ${\displaystyle \iota _{\overline {\epsilon }}}$ dasselbe Bild ${\displaystyle \iota _{\overline {\epsilon }}(\mathbb {C} )=\iota _{\epsilon }(\mathbb {C} )}$ wie ${\displaystyle \iota _{\epsilon }}$ und also ${\displaystyle g_{\overline {\epsilon }}}$ dieselbe Definitionsmenge wie ${\displaystyle g_{\epsilon }}$. Der Funktionswert ${\displaystyle {\begin{array}{llll}{\tilde {g}}(q)&=g_{\overline {\epsilon }}(\xi \,-\,\eta \,{\bar {\epsilon }})=g_{\overline {\epsilon }}(\iota _{\overline {\epsilon }}(\xi -\eta \,\mathrm {i} _{\mathbb {C} }))=\iota _{\overline {\epsilon }}(g(\xi -\eta \,\mathrm {i} _{\mathbb {C} }))\\&=\iota _{\overline {\epsilon }}(u(\xi ,-\eta )\,+\,v(\xi ,-\eta )\mathrm {i} _{\mathbb {C} })&=u(\xi ,-\eta )\,+\,v(\xi ,-\eta ){\bar {\epsilon }}\\&&=u(\xi ,-\eta )\,-\,v(\xi ,-\eta )\epsilon \end{array}}}$ muss also mit dem vorigen für alle ${\displaystyle \xi ,\eta \in \mathbb {R} }$ übereinstimmen. ■

Die eingebettete Funktion ${\displaystyle {\tilde {g}}}$ stimmt auf allen Teilmengen ${\displaystyle \iota _{\epsilon }(\mathbb {C} )\cong \mathbb {C} }$ mit ${\displaystyle g}$ überein, kann also als Fortsetzung von ${\displaystyle g}$ angesehen werden und, wenn Verwechslungen nicht zu befürchten sind, wird auch der Funktionsname beibehalten.

Ist ${\displaystyle g(z)=u(\xi ,\eta )+v(\xi ,\eta )\mathrm {i} _{\mathbb {C} }}$ eine einbettbare Funktion, so ist ${\displaystyle v(\xi ,0)=-v(\xi ,0)}$ wegen der Ungeradheit von ${\displaystyle v}$ in der zweiten Variablen, also ${\displaystyle v(\xi ,0)=0}$ und ${\displaystyle g(z)\in \mathbb {R} }$ für ${\displaystyle z\in \mathbb {R} }$. Somit folgt aus der Einbettbarkeit, dass die Einschränkung aufs Reelle reell ist.[21] Zu dieser Klasse von komplexen Funktionen gehören Norm und Betrag, aber auch alle Laurent-Reihen ${\displaystyle \textstyle \sum _{n=-\infty }^{\infty }a_{n}z^{n}}$ mit reellen Koeffizienten ${\displaystyle a_{n}}$, so die Exponential- und Logarithmusfunktion.[22]

Analysis

Schwieriger ist es, eine allgemeine quaternionische Analysis mit Differential- und/oder Integralrechnung aufzustellen. Ein Problem springt unmittelbar ins Auge: der Begriff des Differenzenquotienten ${\displaystyle {\tfrac {f(x+h)-f(x)}{h}}}$, der in der reellen wie der komplexen Analysis so erfolgreich ist, muss wegen der Nicht-Kommutativität als linke und rechte Version definiert werden. Legt man dann genauso strenge Maßstäbe wie bei der komplexen Differenzierbarkeit an, dann stellt sich heraus, dass bestenfalls lineare Funktionen, und zwar ${\displaystyle x\mapsto a+xb}$ links und ${\displaystyle x\mapsto a+bx}$ rechts, differenzierbar sind.[23] Immer definieren lässt sich aber eine Richtungsableitung und das Gâteaux-Differential.[20]

Ausgehend von den Cauchy-Riemannschen Differentialgleichungen und dem Satz von Morera wurde folgender Regularitätsbegriff gefunden: Eine quaternionische Funktion ist regulär an der Stelle ${\displaystyle x}$, wenn ihr Integral über jeder hinreichend kleinen ${\displaystyle x}$ umschließenden Hyperfläche verschwindet.[24][25][26]

Beschreibung anderer Konstrukte mit Hilfe von Quaternionen

Minkowski-Skalarprodukt

Das Minkowski-Skalarprodukt zweier Quaternionen, aufgefasst als Vektoren im Minkowski-Raum, ist der Skalarteil von ${\displaystyle xy}$:

${\displaystyle x_{0}y_{0}-x_{1}y_{1}-x_{2}y_{2}-x_{3}y_{3}=\operatorname {Re} (xy).}$

Vektoranalysis

Im Folgenden werden Vektoren im dreidimensionalen Raum ${\displaystyle \mathbb {R} ^{3}}$ mit reinen Quaternionen ${\displaystyle \in \operatorname {Im} \,\mathbb {H} }$, also die üblichen ${\displaystyle (x,y,z)}$-Koordinaten mit den ${\displaystyle (x_{1},x_{2},x_{3})}$-Komponenten identifiziert. Definiert man den Nabla-Operator (wie Hamilton) als

${\displaystyle {\vec {\nabla }}\;=\;\mathrm {i} \,{\frac {\partial }{\partial x}}+\mathrm {j} \,{\frac {\partial }{\partial y}}+\mathrm {k} \,{\frac {\partial }{\partial z}}}$

und wendet ihn auf eine skalare Funktion ${\displaystyle f(x,y,z)}$ als (formale) Skalarmultiplikation an, erhält man den Gradienten

${\displaystyle {\vec {\nabla }}f\;=\;\operatorname {grad} f\;=\;\mathrm {i} \,{\frac {\partial f}{\partial x}}+\mathrm {j} \,{\frac {\partial f}{\partial y}}+\mathrm {k} \,{\frac {\partial f}{\partial z}}.}$

Die Anwendung a​uf ein Vektorfeld

${\displaystyle {\vec {F}}(x,y,z)\;=\;\mathrm {i} \,F_{1}(x,y,z)+\mathrm {j} \,F_{2}(x,y,z)+\mathrm {k} \,F_{3}(x,y,z)}$

als (formales) Skalarprodukt ergibt d​ie Divergenz

${\displaystyle {\vec {\nabla }}\cdot {\vec {F}}\;=\;\operatorname {div} {\vec {F}}\;=\;{\frac {\partial F_{1}}{\partial x}}+{\frac {\partial F_{2}}{\partial y}}+{\frac {\partial F_{3}}{\partial z}}}$ .

Die Anwendung a​uf ein Vektorfeld a​ls (formales) Kreuzprodukt ergibt d​ie Rotation

${\displaystyle {\vec {\nabla }}\times {\vec {F}}\;=\;\operatorname {rot} {\vec {F}}\;=\;\mathrm {i} \left({\frac {\partial F_{3}}{\partial y}}-{\frac {\partial F_{2}}{\partial z}}\right)+\mathrm {j} \left({\frac {\partial F_{1}}{\partial z}}-{\frac {\partial F_{3}}{\partial x}}\right)+\mathrm {k} \left({\frac {\partial F_{2}}{\partial x}}-{\frac {\partial F_{1}}{\partial y}}\right)}$ .

Die Anwendung a​uf ein Vektorfeld a​ls (formales) Produkt zweier reiner Quaternionen ergibt

${\displaystyle {\vec {\nabla }}{\vec {F}}\;=\;-\operatorname {div} {\vec {F}}+\operatorname {rot} {\vec {F}}}$

mit ${\displaystyle -\operatorname {div} {\vec {F}}}$ als Skalarteil und ${\displaystyle \operatorname {rot} {\vec {F}}}$ als Vektorteil der Quaternion.

Zweimalige Anwendung auf eine Funktion ${\displaystyle f}$ ergibt den Laplace-Operator ${\displaystyle \triangle }$

${\displaystyle {\vec {\nabla }}^{2}\,f\;:=\;{\vec {\nabla }}\cdot ({\vec {\nabla }}\,f)\;=\;\operatorname {div} \left(\operatorname {grad} \,f\right)\;=\;-\triangle f\;=\;-\left({\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2}}}+{\frac {\partial ^{2}f}{\partial z^{2}}}\right),}$

d. h. ${\displaystyle \nabla }$ wirkt wie ein Dirac-Operator als (formale) „Quadratwurzel“ des (negativen) Laplace-Operators.

Drehungen im dreidimensionalen Raum

Einheitsquaternionen können für eine elegante Beschreibung von Drehungen im dreidimensionalen Raum verwendet werden: Für eine feste Einheitsquaternion ${\displaystyle q}$ ist die Abbildung

${\displaystyle \rho _{q}\colon x\mapsto qxq^{-1}}$   bzw.   ${\displaystyle \rho _{q}\colon x\mapsto qx{\overline {q}}}$

auf ${\displaystyle \operatorname {Im} \,\mathbb {H} }$ eine Drehung. (Hier, wie im Folgenden, ist nur von Drehungen die Rede, die den Ursprung festlassen, d. h. deren Drehachse durch den Ursprung verläuft.)

Die Polardarstellung stellt die Einheitsquaternion ${\displaystyle q\neq \pm 1}$ durch einen Winkel ${\displaystyle 0<\alpha <2\pi }$ und eine reine Einheitsquaternion ${\displaystyle \epsilon }$ eindeutig dar als

${\displaystyle q=\cos {\frac {\alpha }{2}}+\epsilon \sin {\frac {\alpha }{2}}}$ .

Dann ist ${\displaystyle \rho _{q}\ }$ eine Drehung des ${\displaystyle \mathbb {R} ^{3}\ }$ um die Achse ${\displaystyle \epsilon \in \mathbb {R} ^{3}\ }$ mit Drehwinkel ${\displaystyle \alpha }$.

Für jede Einheitsquaternion ${\displaystyle q}$ definieren ${\displaystyle q}$ und ${\displaystyle -q}$ dieselbe Drehung; insbesondere entsprechen ${\displaystyle 1}$ und ${\displaystyle -1}$ beide der identischen Abbildung (Drehung mit Drehwinkel 0). Im Unterschied zur Beschreibung von Drehungen durch orthogonale Matrizen handelt es sich also um keine 1:1-Entsprechung, zu jeder Drehung ${\displaystyle \rho }$ gibt es genau zwei Einheitsquaternionen ${\displaystyle q}$ mit ${\displaystyle \rho _{q}=\rho }$.

Die Hintereinanderausführung v​on Drehungen entspricht d​er Multiplikation d​er Quaternionen, d. h.

${\displaystyle \rho _{q_{1}}\circ \rho _{q_{2}}=\rho _{q_{1}q_{2}}.}$

Die Umkehrung d​er Drehrichtung entspricht d​em Inversen:

${\displaystyle \rho _{q^{-1}}=\rho _{q}^{-1}.}$

Damit ist die Abbildung

${\displaystyle {\begin{array}{rccc}\rho \colon &\mathbb {S} ^{3}&\to &\mathrm {SO} (3)\\&q&\mapsto &\rho _{q}\end{array}}}$

ein Homomorphismus der Gruppe ${\displaystyle \mathbb {S} ^{3}}$ der Einheitsquaternionen in die Drehgruppe ${\displaystyle \mathrm {SO} (3)}$. Sie ist eine Überlagerung der ${\displaystyle \mathrm {SO} (3)}$, und, da ein Bildelement ${\displaystyle \rho _{q}}$ genau die zwei Urbilder ${\displaystyle \pm q\in \mathbb {S} ^{3}}$ hat, zweiblättrig, weshalb der Homomorphismus auch 2:1-Überlagerung(shomomorphismus)[13]^{:Seite 33.} genannt wird. Ferner ist sie universell, da ${\displaystyle \mathrm {SU} (2)\cong \mathbb {S} ^{3}}$ einfach zusammenhängend ist.

Bezug zu orthogonalen Matrizen

Explizit entspricht der Einheitsquaternion ${\displaystyle q\in \mathbb {S} ^{3}}$,

${\displaystyle q=q_{0}+q_{1}\mathrm {i} +q_{2}\mathrm {j} +q_{3}\mathrm {k} }$

mit ${\displaystyle q_{i}\in \mathbb {R} }$ und ${\displaystyle \operatorname {Norm} (q)=q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}=1}$ die Drehmatrix

${\displaystyle {\begin{array}{rlll}D_{q}:=&{\begin{bmatrix}q_{0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}&-2q_{0}q_{3}+2q_{1}q_{2}&2q_{0}q_{2}+2q_{1}q_{3}\\2q_{0}q_{3}+2q_{1}q_{2}&q_{0}^{2}-q_{1}^{2}+q_{2}^{2}-q_{3}^{2}&-2q_{0}q_{1}+2q_{2}q_{3}\\-2q_{0}q_{2}+2q_{1}q_{3}&2q_{0}q_{1}+2q_{2}q_{3}&q_{0}^{2}-q_{1}^{2}-q_{2}^{2}+q_{3}^{2}\end{bmatrix}}\\[.3em]=&{\begin{bmatrix}1-2(q_{2}^{2}+q_{3}^{2})\;\;\;\;&-2q_{0}q_{3}+2q_{1}q_{2}\;\;\;\,&2q_{0}q_{2}+2q_{1}q_{3}\;\;\quad \\2q_{0}q_{3}+2q_{1}q_{2}&1-2(q_{1}^{2}+q_{3}^{2})&-2q_{0}q_{1}+2q_{2}q_{3}\\-2q_{0}q_{2}+2q_{1}q_{3}&2q_{0}q_{1}+2q_{2}q_{3}&1-2(q_{1}^{2}+q_{2}^{2})\end{bmatrix}}\in \mathrm {SO} (3)\end{array}}}$

eine Formel, die auch als Euler-Rodrigues-Formel bekannt ist. Sie bildet eine reine Quaternion ${\displaystyle \xi }$ auf ${\displaystyle (0,D_{q}\;{\vec {\xi }})=q\;\xi \;q^{-1}}$ ab.

Ist umgekehrt d​ie Drehmatrix

${\displaystyle D={\begin{bmatrix}d_{11}&d_{12}&d_{13}\\d_{21}&d_{22}&d_{23}\\d_{31}&d_{32}&d_{33}\end{bmatrix}}\in \mathrm {SO} (3)}$[27]

gegeben u​nd ist d​ie Spur

${\displaystyle T_{D}:=d_{00}+d_{11}+d_{22}+d_{33}>0}$ mit ${\displaystyle d_{00}:=1}$ ,

dann bewerkstelligt d​ie Quaternion

${\displaystyle q_{D}:=T_{D}+(d_{32}-d_{23})\mathrm {i} +(d_{13}-d_{31})\mathrm {j} +(d_{21}-d_{12})\mathrm {k} }$

die Drehung ${\displaystyle D\;{\vec {\xi }}}$, denn es ist ${\displaystyle q_{D}\;\xi \;q_{D}^{-1}=(0,D\;{\vec {\xi }})}$ für jede reine Quaternion ${\displaystyle \xi }$ .

Wenn man die homogen formulierte Version von ${\displaystyle D_{q}}$ als Eingabematrix nimmt, produziert die gezeigte Lösung mit ${\displaystyle d_{00}:=\operatorname {Norm} (q)}$ die Quaternion ${\displaystyle q_{D}=4q_{0}q}$. Wegen ${\displaystyle \operatorname {det} (D_{q})=\operatorname {Norm} (q)^{3}}$ kann die Homogenität in den ${\displaystyle d_{ij}}$ durch die Setzung ${\displaystyle d_{00}:={\sqrt[{3}]{\operatorname {det} (D)}}}$ aufrechterhalten werden.

Die ${\displaystyle \mathrm {SO} (3)}$ hat wie die ${\displaystyle \mathbb {S} ^{3}}$ über ${\displaystyle \mathbb {R} }$ die Dimension 3. Die 9 Komponenten von ${\displaystyle D}$ können also nicht alle frei wählbar sein. Da einer jeden Matrix ${\displaystyle D\in \mathrm {SO} (3)}$ eine Quaternion ${\displaystyle q}$ entspricht, decken die Drehmatrizen ${\displaystyle D_{q}}$ die ganze ${\displaystyle \mathrm {SO} (3)}$ ab. Bei ${\displaystyle D_{q}}$ ist ${\displaystyle T_{D_{q}}=4q_{0}^{2}}$. Falls also ${\displaystyle D}$ wirklich ${\displaystyle \in \mathrm {SO} (3)}$, ist auch ${\displaystyle {\frac {q_{D}}{2{\sqrt {T_{D}}}}}}$ die Einheitsquaternion zu ${\displaystyle q_{D}}$.

Überlegungen z​ur numerischen Stabilität d​es Problems finden s​ich in en:Rotation matrix#Conversions.

Bezug zu Eulerwinkeln

Für Eulerwinkel gibt es verschiedene Konventionen; die folgende Darlegung bezieht sich auf die Drehung, die man erhält, wenn man zuerst um die ${\displaystyle z}$-Achse um den Winkel ${\displaystyle 2\Psi }$, dann um die neue ${\displaystyle x}$-Achse um den Winkel ${\displaystyle 2\Theta }$ und schließlich um die neue ${\displaystyle z}$-Achse um den Winkel ${\displaystyle 2\Phi }$ dreht, d. i. die sog. „x-Konvention“ (z, x’, z’’) mit allen Winkeln doppelt. Die Einzeldrehungen entsprechen den Einheitsquaternionen

${\displaystyle \cos \Psi +\mathrm {k} \,\sin \Psi ,\quad \cos \Theta +\mathrm {i} \,\sin \Theta ,\quad \cos \Phi +\mathrm {k} \,\sin \Phi ,}$

und d​a jeweils u​m die mitgedrehten Achsen gedreht wird, i​st die Reihenfolge d​er Komposition umgekehrt. Die Gesamtdrehung entspricht also

${\displaystyle \left(\cos \Psi +\mathrm {k} \,\sin \Psi \right)\left(\cos \Theta +\mathrm {i} \,\sin \Theta \right)\left(\cos \Phi +\mathrm {k} \,\sin \Phi \right)}$

${\displaystyle {}=\cos \Psi \cos \Theta \cos \Phi -\sin \Psi \cos \Theta \sin \Phi }$

${\displaystyle {}+\mathrm {i} \left(\cos \Psi \sin \Theta \cos \Phi +\sin \Psi \sin \Theta \sin \Phi \right)}$

${\displaystyle {}+\mathrm {j} \left(-\cos \Psi \sin \Theta \sin \Phi +\sin \Psi \sin \Theta \cos \Phi \right)}$

${\displaystyle {}+\mathrm {k} \left(\sin \Psi \cos \Theta \cos \Phi +\cos \Psi \cos \Theta \sin \Phi \right).}$

Für andere Konventionen ergeben s​ich ähnliche Formeln.

Die Eulerwinkel z​u einer gegebenen Quaternion lassen s​ich an d​er zugehörigen Drehmatrix ablesen.[28]

Universelle Überlagerung der Drehgruppe; Spingruppe

Wie im Abschnitt Einheitsquaternionen gezeigt, gibt es einen durch die Hamiltonschen Zahlen vermittelten Isomorphismus zwischen der Gruppe ${\displaystyle \mathbb {S} ^{3}}$ der Einheitsquaternionen und der speziellen unitären Gruppe ${\displaystyle \mathrm {SU} (2)}$. Diese beiden Gruppen sind isomorph zur Spingruppe ${\displaystyle \mathrm {Spin(3)} }$ (zur Physik: siehe Spin).

Die 2:1-Überlagerung liefert also einen Homomorphismus der Spingruppe ${\displaystyle \mathrm {Spin(3)} }$ in die Drehgruppe ${\displaystyle \mathrm {SO} (3)}$. Diese Überlagerung ist zweiblättrig und universell, da ${\displaystyle \mathrm {Spin(3)} \cong \mathrm {SU} (2)\cong \mathbb {S} ^{3}}$ im Gegensatz zur ${\displaystyle \mathrm {SO} (3)}$ einfach zusammenhängend ist. Die natürliche Operation von ${\displaystyle \mathrm {SU} (2)}$ auf ${\displaystyle \mathbb {C} ^{2}}$ ist eine sog. Spinordarstellung.

Die aus der Quantenmechanik bekannten sog. Pauli-Matrizen ${\displaystyle \sigma _{1},\sigma _{2},\sigma _{3}}$ stehen in einfacher Beziehung zu den drei Erzeugenden ${\displaystyle \mathrm {i} ,\mathrm {j} ,\mathrm {k} }$ der ${\displaystyle \mathrm {SU} (2)}$. Dies wird besonders deutlich in der Darstellung als komplexe Matrizen:

${\displaystyle \sigma _{1}={\begin{bmatrix}0&1\\1&0\end{bmatrix}}=-\mathrm {i} _{\mathbb {C} }\mathrm {k} ,\quad \sigma _{2}={\begin{bmatrix}0&-\mathrm {i} _{\mathbb {C} }\\\mathrm {i} _{\mathbb {C} }&0\end{bmatrix}}=-\mathrm {i} _{\mathbb {C} }\mathrm {j} ,\quad \sigma _{3}={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}=-\mathrm {i} _{\mathbb {C} }\mathrm {i} }$ ,

dabei ist ${\displaystyle \mathrm {i} _{\mathbb {C} }}$ die imaginäre Einheit der komplexen Zahlen.

Die Pauli-Matrizen h​aben −1 z​ur Determinante (sind a​lso keine Quaternionen), s​ind spurfrei u​nd hermitesch u​nd kommen d​aher in d​er Quantenmechanik a​ls messbare Größen i​n Frage, w​as sich für d​ie Anwendungen (s. mathematische Struktur d​er Quantenmechanik) a​ls wichtig erwiesen hat. Einzelheiten s​ind im Artikel SU(2) dargestellt.

Orthogonale Abbildungen des vierdimensionalen Raumes

Analog zum dreidimensionalen Fall kann man jede orientierungserhaltende orthogonale Abbildung von ${\displaystyle \mathbb {H} }$ in sich selbst in der Form

${\displaystyle \rho _{a,b}\colon x\mapsto ax{\bar {b}}}$

für Einheitsquaternionen ${\displaystyle a,b}$ beschreiben. Es gilt

${\displaystyle \rho _{a_{1},b_{1}}\circ \rho _{a_{2},b_{2}}=\rho _{a_{1}a_{2},b_{1}b_{2}}\quad {\text{und}}\quad \rho _{{\bar {a}},{\bar {b}}}=\rho _{a,b}^{-1}.}$

Diese Konstruktion liefert e​ine Überlagerung

${\displaystyle \mathrm {SU} (2)\times \mathrm {SU} (2)\to \mathrm {SO} (4)}$

mit Kern ${\displaystyle \{(1,1),(-1,-1)\}}$.

Die endlichen Untergruppen

Der 2:1-Überlagerungshomomorphismus

${\displaystyle \rho \colon q\mapsto \rho _{q}}$,

der einer Einheitsquaternion ${\displaystyle q\in \mathbb {S} ^{3}}$ die 3D-Drehung

${\displaystyle {\begin{array}{rccc}\rho _{q}\colon &\operatorname {Im} \,\mathbb {H} &\to &\operatorname {Im} \,\mathbb {H} \\&x&\mapsto &qx{\bar {q}}\end{array}}}$

zuordnet, muss eine endliche Gruppe ${\displaystyle Q}$ von Quaternionen in eine endliche Gruppe ${\displaystyle \rho (Q):=\{\rho _{q}\mid q\in Q\}}$ überführen, die dann eine endliche Drehgruppe im ${\displaystyle \mathbb {R} ^{3}}$ ist. Man findet zyklische Gruppen ${\displaystyle \mathrm {C} _{n}}$ und Polyedergruppen, also die Diedergruppen ${\displaystyle \mathrm {D} _{n}}$ (Zählweise der n-Ecke), die Tetraedergruppe ${\displaystyle \mathrm {T} }$, die Oktaedergruppe ${\displaystyle \mathrm {O} }$ und die Ikosaedergruppe ${\displaystyle \mathrm {I} }$.

Die Erzeugenden der zyklischen Gruppen sind Einbettungen von Einheitswurzeln ${\displaystyle \exp(2\pi \mathrm {i} _{\mathbb {C} }/n)}$.[29] Die Urbilder der ${\displaystyle \mathrm {D} _{n}}$, ${\displaystyle \mathrm {T} }$, ${\displaystyle \mathrm {O} }$, ${\displaystyle \mathrm {I} }$ unter ${\displaystyle \rho }$ werden mit ${\displaystyle \mathrm {2D} _{n}}$, ${\displaystyle \mathrm {2T} }$, ${\displaystyle \mathrm {2O} }$, ${\displaystyle \mathrm {2I} }$ bezeichnet und heißen binäre Diedergruppe etc. Für eine Polyedergruppe ${\displaystyle \mathrm {P} }$ ist also ${\displaystyle \mathrm {2P}$ :=\{q\mid \rho _{q}\in \mathrm {P} \}} .[30]

Die endlichen Gruppen von Quaternionen sind demnach[13]^{: 3.5 The Finite Groups of Quaternions, S. 33} ${\displaystyle (2\leq n\in \mathbb {Z} )}$ :

Gruppe	erzeugt von	Ordnung	konvexe Hülle im ${\displaystyle \mathbb {R} ^{2}}$ bzw. ${\displaystyle \mathbb {R} ^{4}}$
${\displaystyle \mathrm {C} _{n}}$	${\displaystyle \langle e_{n}\rangle }$	${\displaystyle n}$	reguläres n-Eck
${\displaystyle \mathrm {2D} _{n}}$	${\displaystyle \langle e_{2n},\mathrm {j} \rangle }$	${\displaystyle 4n}$	${\displaystyle \{2n\}\Box \{2n\}}$[31], bei n=2 zugleich: regulärer 16-Zeller
${\displaystyle \mathrm {2T} }$	${\displaystyle \langle \mathrm {i} ,\omega \rangle }$	${\displaystyle 24}$	regulärer 24-Zeller
${\displaystyle \mathrm {2O} }$	${\displaystyle \langle q_{O},\omega \rangle }$	${\displaystyle 48}$	${\displaystyle {\text{f}}_{1,2}{\text{F}}_{4}}$[31] = Dihektaoktokontaoktochor (288-Zeller)
${\displaystyle \mathrm {2I} }$	${\displaystyle \langle q_{I},\omega \rangle }$	${\displaystyle 120}$	regulärer 600-Zeller

mit

${\displaystyle e_{n}:=\exp(2\pi \mathrm {i} /n)}$ ,   ${\displaystyle \omega$ :={\frac {-1+\mathrm {i} +\mathrm {j} +\mathrm {k} }{2}}}  ,   ${\displaystyle q_{O}:={\frac {\mathrm {j} +\mathrm {k} }{\sqrt {2}}}}$ ,   ${\displaystyle q_{I}:={\frac {2\mathrm {i} +({\sqrt {5}}+1)\mathrm {j} +({\sqrt {5}}-1)\mathrm {k} }{4}}}$ .

Die zyklischen Gruppen ${\displaystyle \mathrm {C} _{n}}$ sind in naheliegender Weise Untergruppen von anderen Gruppen. Die Quaternionengruppe ${\displaystyle \mathrm {Q} _{8}}$ = ${\displaystyle \mathrm {2D} _{2}}$ ist eine Untergruppe der binären Tetraedergruppe ${\displaystyle \mathrm {2T} }$. Die Automorphismengruppe von ${\displaystyle \mathrm {Q} _{8}}$ ist isomorph zur Oktaedergruppe ${\displaystyle \mathrm {O} =\mathrm {Sym} _{4}}$ (Symmetrische Gruppe). Ihre Elemente sind ebenfalls Automorphismen von ${\displaystyle \mathrm {2T} }$, ${\displaystyle \mathrm {2O} }$, ${\displaystyle \mathrm {2I} }$ und ${\displaystyle \mathbb {H} }$.

Die konvexen Hüllen sind (bis auf die Fälle ${\displaystyle \mathrm {C} _{n}}$, bei denen man mit 2 Dimensionen auskommt) 4-Polytope und haben, da alle Gruppenelemente von der Länge 1 sind, die Einheits-3-Sphäre ${\displaystyle \mathbb {S} ^{3}}$ als Um-3-Sphäre. Die Ränder dieser 4-Polytope, also die Zellen, sind Ansammlungen von Tetraedern – bis auf den Fall ${\displaystyle \mathrm {2T} }$, bei dem es Oktaeder sind. Bei den regulären unter den konvexen Hüllen ist es klar, dass die Zellen ebenfalls regulär und zueinander kongruent sind und es eine In-3-Sphäre gibt, die alle Zellen (an ihrem Mittelpunkt) berührt. Die übrigen, nämlich ${\displaystyle \mathrm {2D} _{n}}$ und ${\displaystyle \mathrm {2O} }$, spannen sog. perfekte[31] 4-Polytope auf. Hier sind die Zellen tetragonale Disphenoide, welche ebenfalls alle zueinander kongruent sind und an ihrem Mittelpunkt von der In-3-Sphäre berührt werden.

Automorphismen

Ein jeder Ring-Automorphismus ${\displaystyle \sigma }$ von ${\displaystyle \mathbb {H} }$ ist ein innerer,[32] d. h. es gibt eine Quaternion ${\displaystyle q}$, so dass ${\displaystyle \sigma \colon x\mapsto qxq^{-1}}$. Daraus folgt:

• Das Zentrum ${\displaystyle \mathbb {R} }$ bleibt fest, d. h. ${\displaystyle \sigma (\lambda )=\lambda }$ für alle ${\displaystyle \lambda \in \mathbb {R} }$.
• Man kann sich auf die Einheitsquaternionen ${\displaystyle q\in \mathbb {S} ^{3}}$ beschränken.
• Ein Automorphismus ändert nicht das Skalarprodukt, d. h. ${\displaystyle \sigma (x)\cdot \sigma (y)=x\cdot y}$.
• Die Automorphismen sind genau die winkel- und längentreuen Drehungen von ${\displaystyle \operatorname {Im} \,\mathbb {H} }$ aus dem Abschnitt Drehungen im dreidimensionalen Raum.
• Wegen der Längentreue sind die Automorphismen stetig, somit zusätzlich topologisch.
• ${\displaystyle \mathbb {S} ^{3}}$ hat das Zentrum ${\displaystyle \{\pm 1\}}$. Folglich ist die Automorphismengruppe ${\displaystyle \mathrm {Aut} (\mathbb {H} )\cong \mathbb {S} ^{3}/\{\pm 1\}}$.

Die Konjugation als Spiegelung an der reellen Achse ist antihomomorph[33] in der Multiplikation, d. h. ${\displaystyle {\overline {xy}}={\bar {y}}{\bar {x}}}$, und wird als involutiver Antiautomorphismus bezeichnet, weil sie zudem eine Involution ist.

Andere Konstruktionen

Komplexe Matrizen

Im Ring ${\displaystyle \mathbb {C} ^{2\times 2}}$ der komplexen 2×2-Matrizen bildet man den von den Elementen

${\displaystyle 1_{H}:={\begin{bmatrix}1&0\\0&1\end{bmatrix}},\quad \mathrm {i} _{H}:={\begin{bmatrix}\mathrm {i} _{\mathbb {C} }&0\\0&-\mathrm {i} _{\mathbb {C} }\end{bmatrix}},\quad \mathrm {j} _{H}:={\begin{bmatrix}0&1\\-1&0\end{bmatrix}},\quad \mathrm {k} _{H}:={\begin{bmatrix}0&\mathrm {i} _{\mathbb {C} }\\\mathrm {i} _{\mathbb {C} }&0\end{bmatrix}}}$

erzeugten Unterring ${\displaystyle H}$[34], wobei die imaginäre Einheit der komplexen Zahlen als ${\displaystyle \mathrm {i} _{\mathbb {C} }}$ kenntlich gemacht ist.[35] Eine Matrix

${\displaystyle x_{0}\,1_{H}+x_{1}\,\mathrm {i} _{H}+x_{2}\,\mathrm {j} _{H}+x_{3}\,\mathrm {k} _{H}={\begin{bmatrix}x_{0}+x_{1}\,\mathrm {i} _{\mathbb {C} }\quad &x_{2}+x_{3}\,\mathrm {i} _{\mathbb {C} }\\-x_{2}+x_{3}\,\mathrm {i} _{\mathbb {C} }\quad &x_{0}-x_{1}\,\mathrm {i} _{\mathbb {C} }\end{bmatrix}}\;=\;{\begin{bmatrix}w&z\\-{\overline {z}}&{\overline {w}}\end{bmatrix}}}$

mit reellen ${\displaystyle x_{0},x_{1},x_{2},x_{3}}$ und komplexen ${\displaystyle w:=x_{0}+x_{1}\mathrm {i} _{\mathbb {C} },z:=x_{2}+x_{3}\mathrm {i} _{\mathbb {C} }}$ hat die Determinante ${\displaystyle x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=|w|^{2}+|z|^{2}}$, die nur dann 0 ist, wenn ${\displaystyle (w,z)=(0,0)}$. Somit sind alle von der Nullmatrix verschiedenen Matrizen invertierbar – und der Ring ${\displaystyle H}$ ist ein Schiefkörper.[36]

Der so konstruierte Schiefkörper erweist sich als isomorph zu den Quaternionen. Denn die Abbildung ${\displaystyle \mathbb {H} \to H}$ mit den Zuordnungen

${\displaystyle 1\mapsto 1_{H},\quad \mathrm {i} \mapsto \mathrm {i} _{H},\quad \mathrm {j} \mapsto \mathrm {j} _{H},\quad \mathrm {k} \mapsto \mathrm {k} _{H}}$

ist homomorph i​n den Verknüpfungen Addition u​nd Multiplikation, w​obei letztere d​er Matrizenmultiplikation zuzuordnen ist. Die konjugierte Quaternion g​eht auf d​ie adjungierte Matrix u​nd die Norm a​uf die Determinante. Darüber hinaus i​st die Abbildung injektiv u​nd stetig, a​lso topologisch.

Es gibt verschiedene Möglichkeiten für die Einbettung ${\displaystyle \mathbb {H} \to H}$, die alle zueinander konjugiert und homöomorph sind.[37]

Reelle Matrizen

Ganz analog kann man die Quaternion ${\displaystyle x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} }$ auch als reelle 4×4-Matrix

${\displaystyle {\begin{bmatrix}{\begin{array}{rrrr}x_{0}&x_{1}&x_{2}&x_{3}\\-x_{1}&x_{0}&-x_{3}&x_{2}\\-x_{2}&x_{3}&x_{0}&-x_{1}\\-x_{3}&-x_{2}&x_{1}&x_{0}\end{array}}\end{bmatrix}}}$

${\displaystyle =x_{0}\left[{\begin{smallmatrix}{\begin{array}{rrrr}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\end{smallmatrix}}\right]+x_{1}\left[{\begin{smallmatrix}{\begin{array}{rrrr}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{array}}\end{smallmatrix}}\right]+x_{2}\left[{\begin{smallmatrix}{\begin{array}{rrrr}0&0&1&0\\0&0&0&1\\-1&0&0&0\\0&-1&0&0\end{array}}\end{smallmatrix}}\right]+x_{3}\left[{\begin{smallmatrix}{\begin{array}{rrrr}0&0&0&1\\0&0&-1&0\\0&1&0&0\\-1&0&0&0\end{array}}\end{smallmatrix}}\right]}$

schreiben. Die Konjugation d​er Quaternion entspricht d​er Transposition d​er Matrix u​nd der Betrag d​er vierten Wurzel a​us der Determinante.

Das Modell d​er reellen Matrizen i​st bspw. d​ann vorteilhaft, w​enn man e​ine Software für lineare Algebra m​it Schwächen b​ei den komplexen Zahlen hat.

Quotientenalgebra

Eine elegante, aber zugleich abstrakte Konstruktion stellt der Weg über den Quotienten des nichtkommutativen Polynomrings in drei Unbestimmten dar, deren Bilder ${\displaystyle \mathrm {i} ,\mathrm {j} ,\mathrm {k} }$ sind, modulo dem Ideal, das von den Hamilton-Regeln erzeugt wird. Alternativ kommt man auch mit nur zwei Unbestimmten aus.

Auf diese Weise ergibt sich die Quaternionen-Algebra als Clifford-Algebra der zweidimensionalen, euklidischen Ebene mit Erzeugern ${\displaystyle \mathrm {i} \mapsto e_{1},\,\mathrm {j} \mapsto e_{2},\,\mathrm {k} =\mathrm {ij} \mapsto e_{1}e_{2}}$. Im Zusammenhang mit dreidimensionalen Drehungen ist auch die Interpretation als der gerade Anteil der Clifford-Algebra des dreidimensionalen, euklidischen Raumes wichtig. Die Erzeuger werden dann mit ${\displaystyle \mathrm {i} \mapsto e_{2}e_{3},\,\mathrm {j} \mapsto e_{3}e_{1},\,\mathrm {k} \mapsto e_{1}e_{2}}$ identifiziert.

Die Quaternionen als Algebra

Es gibt bis auf Isomorphie genau vier endlichdimensionale ${\displaystyle \mathbb {R} }$-Algebren, deren Multiplikation ohne Nullteiler ist, nämlich den Körper ${\displaystyle \mathbb {R} }$ der reellen Zahlen selbst, den Körper ${\displaystyle \mathbb {C} }$ der komplexen Zahlen, den Schiefkörper ${\displaystyle \mathbb {H} }$ der Quaternionen und den Alternativkörper ${\displaystyle \mathbb {O} }$ der Cayleyschen Oktaven.[38][39][40]

Das Zentrum von ${\displaystyle \mathbb {H} }$ ist ${\displaystyle \mathbb {R} }$; die Quaternionen sind also eine zentraleinfache Algebra über ${\displaystyle \mathbb {R} }$. Reduzierte Norm und Spur sind durch

${\displaystyle \mathrm {Nrd} (x)=|x|^{2}=x{\bar {x}}={\bar {x}}x=\langle x,x\rangle }$      bzw.      ${\displaystyle \mathrm {Trd} (x)=2\cdot \operatorname {Re} \,x}$

gegeben.

Beim Basiswechsel von ${\displaystyle \mathbb {R} }$ zum algebraischen Abschluss ${\displaystyle \mathbb {C} }$ werden die Quaternionen zu einer Matrizenalgebra:

${\displaystyle \mathbb {H} \otimes _{\mathbb {R} }\mathbb {C} \cong M_{2}(\mathbb {C} ).}$

Die komplexe Konjugation auf dem Faktor ${\displaystyle \mathbb {C} }$ des Tensorproduktes entspricht einer Involution ${\displaystyle v}$ der Matrizenalgebra. Die Invarianten von ${\displaystyle v}$, d. s. die von ${\displaystyle v}$ fix gelassenen Elemente ${\displaystyle x}$ mit ${\displaystyle v(x)=x}$, bilden eine zu ${\displaystyle \mathbb {H} }$ isomorphe Algebra. Zur oben angegebenen Matrixdarstellung der Quaternionen als komplexe Matrizen passt die Involution

${\displaystyle v(x):=\epsilon {\bar {x}}\epsilon ^{-1}}$   mit   ${\displaystyle \epsilon$ :={\begin{bmatrix}0&1\\-1&0\end{bmatrix}}}  .

Die Tatsache, dass die Brauergruppe von ${\displaystyle \mathbb {R} }$ nur aus zwei Elementen besteht, spiegelt sich auch darin wider, dass

${\displaystyle \mathbb {H} \otimes _{\mathbb {R} }\mathbb {H} \cong M_{4}(\mathbb {R} )}$

ist.

Allgemein bezeichnet m​an jede vierdimensionale zentraleinfache Algebra über e​inem Körper a​ls eine Quaternionenalgebra.

Die Quaternionen sind die Clifford-Algebra zum Raum ${\displaystyle \mathbb {R} ^{2}}$ mit einer negativ-definiten symmetrischen Bilinearform.

Andere Grundkörper

Quaternionen über den rationalen Zahlen

Bei allen obigen Arten der Konstruktion spielt die Vollständigkeit des Koeffizientenvorrats keine Rolle. Deshalb kann man (anstatt von den reellen Zahlen ${\displaystyle \mathbb {R} \,}$ über ${\displaystyle \mathbb {C} =\mathbb {R} (\mathrm {i} )\,}$ zu ${\displaystyle \mathbb {H} \,}$) auch von anderen Grundkörpern, z. B. den rationalen Zahlen ${\displaystyle \mathbb {Q} \,}$, ausgehen, um via gaußsche Zahlen ${\displaystyle \mathbb {Q} (\mathrm {i} )\,}$ bei den Quaternionen mit rationalen Koeffizienten

${\displaystyle G:=\{x_{0}+x_{1}\mathrm {i} +x_{2}\mathrm {j} +x_{3}\mathrm {k} \;\mid \;x_{0},x_{1},x_{2},x_{3}\in \mathbb {Q} \}\,}$

anzukommen – mit formal denselben Rechenregeln. Danach kann, falls überhaupt erforderlich, die Vervollständigung für die Betragsmetrik durchgeführt werden mit einem Endergebnis isomorph zu ${\displaystyle \mathbb {H} \,}$.

Insofern kann bei vielen Aussagen ${\displaystyle \mathbb {R} \,}$ durch ${\displaystyle \mathbb {Q} \,}$, ${\displaystyle \mathbb {C} \,}$ durch ${\displaystyle \mathbb {Q} (\mathrm {i} )\,}$ und ${\displaystyle \mathbb {H} \,}$ durch ${\displaystyle G\,}$ ersetzt werden.

Da es nach dem Satz von Wedderburn keinen endlichen Schiefkörper mit nicht-kommutativer Multiplikation gibt und die Dimension des Vektorraums ${\displaystyle G\,}$ über seinem Primkörper und Zentrum ${\displaystyle \mathbb {Q} \,}$ mit ${\displaystyle 2^{2}=4\,}$ minimal ist, gehört ${\displaystyle G\,}$ als abzählbare Menge zu den „kleinsten“ Schiefkörpern mit nicht-kommutativer Multiplikation – auf jeden Fall enthält ${\displaystyle G\,}$ keinen kleineren.

Der Schiefkörper ${\displaystyle G\,}$ besitzt einen sogenannten Ganzheitsring, d. h. eine Untermenge von Zahlen, genannt Hurwitzquaternionen, die einen Ring bilden und ${\displaystyle G\,}$ zum Quotientenkörper haben, – ganz ähnlich, wie es sich bei den ganzen Zahlen ${\displaystyle \mathbb {Z} \,}$ und ihrem Quotientenkörper ${\displaystyle \mathbb {Q} \,}$ verhält. In einem solchen Ring lassen sich bspw. Approximationsfragen, Teilbarkeitsfragen u. Ä. untersuchen.

→ Hauptartikel: Hurwitzquaternion

Weitere Grundkörper

Auch Körper ${\displaystyle K\ncong \mathbb {Q} \,}$ eignen sich als Ausgangspunkt zur Bildung nicht-kommutativer Erweiterungskörper nach Art der Quaternionen. Wichtig ist, dass in ${\displaystyle K\,}$ die Summe aus 4 Quadraten ${\displaystyle x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\,}$ nur für ${\displaystyle x_{0}=x_{1}=x_{2}=x_{3}=0\,}$ verschwindet. Dann gibt es auch kein ${\displaystyle \mathrm {i} \in K\,}$ mit ${\displaystyle \mathrm {i} ^{2}+1=0\,}$ und ${\displaystyle K(\mathrm {i} )\,}$ ist eine echte quadratische Erweiterung, die eine Konjugation definiert. Diese Bedingungen sind z. B. bei allen formal reellen Körpern erfüllt.

Aber auch bei Körpern, die nicht angeordnet werden können, kann die obige Bedingung betreffend die Summe aus 4 Quadraten erfüllt sein, bspw. im Körper ${\displaystyle \mathbb {Q} _{2}}$ der 2-adischen Zahlen. Der so über ${\displaystyle \mathbb {Q} _{2}}$ gebildete Quaternionenkörper ist isomorph zur Vervollständigung des (oben beschriebenen) Körpers ${\displaystyle G}$ der Quaternionen mit rationalen Koeffizienten für die folgende (nichtarchimedische diskrete) Bewertung ${\displaystyle v}$ , dem 2-Exponenten der Norm,

${\displaystyle {\begin{array}{rccccc}v\colon &G^{*}&\xrightarrow {\operatorname {Norm} } &\mathbb {Q} ^{*}&\xrightarrow {v_{2}} &\mathbb {Z} \\&x&\mapsto &x{\bar {x}}&\mapsto &v_{2}(x{\bar {x}})\end{array}}}$

mit ${\displaystyle \operatorname {Norm} (x)=x{\bar {x}}=2^{n}m,n\in \mathbb {Z} ,m\in \mathbb {Q} ^{*},2\nmid m,2\nmid m^{-1}}$ . Die Primzahl ${\displaystyle p=2}$ ist die einzige, für die die Quaternionen-Algebra über ${\displaystyle \mathbb {Q} _{p}}$ nullteilerfrei und ein Schiefkörper ist.

Anwendungen

Eulerscher Vier-Quadrate-Satz

Die Identität, d​ie aus d​em Produkt zweier Summen v​on vier Quadraten

${\displaystyle (x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2})(y_{0}^{2}+y_{1}^{2}+y_{2}^{2}+y_{3}^{2})}$

	${\displaystyle =(x_{0}y_{0}-x_{1}y_{1}-x_{2}y_{2}-x_{3}y_{3})^{2}}$
	${\displaystyle +\;(x_{0}y_{1}+x_{1}y_{0}+x_{2}y_{3}-x_{3}y_{2})^{2}}$
	${\displaystyle +\;(x_{0}y_{2}-x_{1}y_{3}+x_{2}y_{0}+x_{3}y_{1})^{2}}$
	${\displaystyle +\;(x_{0}y_{3}+x_{1}y_{2}-x_{2}y_{1}+x_{3}y_{0})^{2}}$

wieder eine Summe von vier Quadraten macht, gilt universell – einschließlich aller Varianten, die durch Vorzeichenspiel und Permutation entstehen, – in jedem Polynomring ${\displaystyle R[x_{0},x_{1},x_{2},x_{3},y_{0},y_{1},y_{2},y_{3}]}$ über einem kommutativen unitären Ring ${\displaystyle R}$ und kann im Nachhinein als „Abfallprodukt“ der Multiplikativität des quaternionischen Betrags angesehen werden. Ihre Entdeckung 1748, also lange vor der Quaternionenzeit, geht jedoch auf Leonhard Euler zurück, der mit ihrer Hilfe den 1770 erstmals erbrachten Beweis von Joseph-Louis Lagrange für den lange vermuteten Vier-Quadrate-Satz wesentlich vereinfachen konnte.

Informatik und Ingenieurwissenschaften

Die Darstellung von Drehungen mithilfe von Quaternionen wird heutzutage im Bereich der interaktiven Computergrafik genutzt, insbesondere bei Computerspielen, sowie bei der Steuerung und Regelung von Satelliten. Bei Verwendung von Quaternionen an Stelle von Drehmatrizen werden etwas weniger Rechenoperationen benötigt. Insbesondere, wenn viele Drehungen miteinander kombiniert (multipliziert) werden, steigt die Verarbeitungsgeschwindigkeit. Des Weiteren werden Quaternionen, neben den Eulerwinkeln, zur Programmierung von Industrierobotern (z. B. ABB) genutzt.

Physik

Durch d​ie Verwendung d​er Quaternionen k​ann man i​n vielen Fällen a​uf getrennte Gleichungen z​ur Berechnung v​on Zeit u​nd Raum verzichten. Dies bietet Vorteile i​n der Physik, u​nter anderem i​n den Gebieten Mechanik, Wellengleichungen, Spezielle Relativitätstheorie u​nd Gravitation, Elektromagnetismus s​owie der Quantenmechanik.

Wie i​m Abschnitt Vektoranalysis werden Vektoren i​m dreidimensionalen Raum m​it reinen Quaternionen identifiziert.

Elektromagnetismus

Die Maxwell-Gleichungen z​ur Beschreibung d​es Elektromagnetismus s​ind der bekannteste Anwendungsfall für Quaternionen. Die Maxwellgleichungen werden d​urch eine Gruppe v​on Kommutatoren u​nd Antikommutatoren d​es Differenzoperators, d​es elektrischen Feldes E u​nd dem magnetischen Feld B i​m Vakuum definiert. Im Wesentlichen s​ind dieses d​ie homogene Maxwellgleichung u​nd das gaußsche Gesetz.

Im Folgenden werden modifizierte Kommutatoren bzw. Antikommutatoren verwendet:

${\displaystyle \operatorname {Ungerade} \left\langle x;y\right\rangle \;:=\;{\frac {x\,y-y\,x}{2}}\;=\;(0,\,{\vec {x}}\times {\vec {y}})}$[41]

bzw.

${\displaystyle \operatorname {Gerade} \left\langle x;y\right\rangle \;:=\;{\frac {x\,y+y\,x}{2}}\;=\;(x_{0}y_{0}-{\vec {x}}\cdot {\vec {y}},\,x_{0}{\vec {y}}+{\vec {x}}y_{0})}$[41]

und

${\displaystyle {\overrightarrow {\operatorname {Gerade} \left\langle x;y\right\rangle }}\;=\;x_{0}{\vec {y}}+{\vec {x}}y_{0}}$

mit ${\displaystyle x,y}$ als (formalen) Quaternionen und diversen formalen Produkten.

Die homogene Maxwellgleichung i​st definiert durch:

${\displaystyle \operatorname {Gerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);\left(0,{\vec {B}}\right)\right\rangle +\operatorname {Ungerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);\left(0,{\vec {E}}\right)\right\rangle }$

${\displaystyle =\left(-{\vec {\nabla }}\cdot {\vec {B}},{\vec {\nabla }}\times {\vec {E}}+{\frac {\partial {\vec {B}}}{\partial t}}\right)=\left(0,{\vec {0}}\right)}$ .

Hierbei besagt ${\displaystyle -{\vec {\nabla }}\cdot {\vec {B}}=0}$, dass keine magnetischen Monopole existieren. ${\displaystyle \textstyle {\vec {\nabla }}\times {\vec {E}}+{\frac {\partial {\vec {B}}}{\partial t}}={\vec {0}}}$ ist das Faradaysche Induktionsgesetz.

Das gaußsche Gesetz definiert s​ich umgekehrt aus:

${\displaystyle \operatorname {Ungerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);\left(0,{\vec {B}}\right)\right\rangle -\operatorname {Gerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);\left(0,{\vec {E}}\right)\right\rangle }$

${\displaystyle =\left({\vec {\nabla }}\cdot {\vec {E}},{\vec {\nabla }}\times {\vec {B}}-{\frac {\partial {\vec {E}}}{\partial t}}\right)=4\,\pi \,\left(\rho ,{\vec {J}}\right)}$ .

Hierbei ergibt ${\displaystyle {\vec {\nabla }}\cdot {\vec {E}}}$ das gaußsche Gesetz und ${\displaystyle \textstyle {\vec {\nabla }}\times {\vec {B}}-{\frac {\partial {\vec {E}}}{\partial t}}}$ das von Maxwell korrigierte Ampèresche Durchflutungsgesetz.

Elektromagnetisches Viererpotential

Die elektrischen u​nd magnetischen Felder werden häufig a​ls elektromagnetisches Viererpotential (d. h. a​ls 4-wertiger Vektor) ausgedrückt. Dieser Vektor k​ann auch a​ls Quaternion umformuliert werden.

${\displaystyle E={\overrightarrow {\operatorname {Gerade} \left\langle \left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right);\left(\phi ,-{\vec {A}}\right)\right\rangle }}=\left(0,-{\frac {\partial {\vec {A}}}{\partial t}}-{\vec {\nabla }}\phi \right)}$

${\displaystyle B=\operatorname {Ungerade} \left\langle \left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right);\left(\phi ,-{\vec {A}}\right)\right\rangle =\left(0,{\vec {\nabla }}\times {\vec {A}}\right)}$

Das elektrische Feld E i​st der Antikommutator d​es konjugierten, differenzierten Vierpotenzials. Das magnetische Feld B verwendet d​en Kommutator. Durch d​iese Darstellungsform k​ann man direkt i​n die Maxwellgleichungen einsetzen:

${\displaystyle \operatorname {Gerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);\operatorname {Ungerade} \left\langle \left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right);\left(\phi ,-{\vec {A}}\right)\right\rangle \right\rangle }$

${\displaystyle +\operatorname {Ungerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);{\overrightarrow {\operatorname {Gerade} \left\langle \left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right);\left(\phi ,-{\vec {A}}\right)\right\rangle }}\right\rangle }$

${\displaystyle =\left(-{\vec {\nabla }}\cdot {\vec {\nabla }}\times {\vec {A}},{\frac {\partial \,{\vec {\nabla }}{\vec {A}}}{\partial t}}-{\vec {\nabla }}\times {\frac {\partial {\vec {A}}}{\partial t}}-{\vec {\nabla }}\times {\vec {\nabla }}\,\phi \right)}$

${\displaystyle =\left(-{\vec {\nabla }}\cdot {\vec {B}},{\vec {\nabla }}\times {\vec {E}}+{\frac {\partial {\vec {B}}}{\partial t}}\right)=\left(0,{\vec {0}}\right)}$

sowie

${\displaystyle \operatorname {Ungerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);\operatorname {Ungerade} \left\langle \left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right);\left(\phi ,{\vec {A}}\right)\right\rangle \right\rangle }$

${\displaystyle -\operatorname {Gerade} \left\langle \left({\frac {\partial }{\partial t}},{\vec {\nabla }}\right);{\overrightarrow {\operatorname {Gerade} \left\langle \left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right);\left(\phi ,-{\vec {A}}\right)\right\rangle }}\right\rangle }$

${\displaystyle =\left(-{\vec {\nabla }}\cdot {\vec {\nabla }}\,\phi -{\vec {\nabla }}\cdot {\frac {\partial {\vec {A}}}{\partial t}},{\vec {\nabla }}\times {\vec {\nabla }}\times {\vec {A}}+{\frac {\partial ^{2}{\vec {A}}}{\partial t^{2}}}+{\frac {\partial {\vec {\nabla }}\phi }{\partial t}}\right)}$

${\displaystyle =\left({\vec {\nabla }}\cdot {\vec {E}},{\vec {\nabla }}\times {\vec {B}}+{\frac {\partial {\vec {E}}}{\partial t}}\right)=4\,\pi \,\left(\rho ,{\vec {J}}\right)}$ .

Hierbei sind die Ausdrücke ${\displaystyle -{\vec {\nabla }}\cdot {\vec {B}}}$ und ${\displaystyle {\vec {\nabla }}\cdot {\vec {E}}}$ die beiden Quellenfelder, die durch die Differenz aus zwei Kommutatoren und zwei Antikommutatoren gebildet werden.

Das Induktionsgesetz ${\displaystyle \textstyle {\vec {\nabla }}\times {\vec {E}}+{\frac {\partial {\vec {B}}}{\partial t}}=0}$ und das Durchflutungsgesetz ${\displaystyle \textstyle {\vec {\nabla }}\times {\vec {B}}+{\frac {\partial {\vec {E}}}{\partial t}}=4\,\pi \,{\vec {J}}}$ werden durch die Summe aus den zwei ineinanderliegenden Kommutatoren und Antikommutatoren gebildet.

Lorentzkraft

Die Lorentzkraft w​ird auf ähnliche Weise a​us den Maxwellgleichungen abgeleitet. Allerdings müssen d​ie Vorzeichen korrigiert werden.

${\displaystyle \operatorname {Ungerade} \left\langle \left(\gamma ,\gamma \,{\vec {\beta }}\right);\left(0,{\vec {B}}\right)\right\rangle -\operatorname {Gerade} \left\langle \left(-\gamma ,\gamma {\vec {\beta }}\right);\left(0,{\vec {E}}\right)\right\rangle }$

${\displaystyle =\left(\gamma \,{\vec {\beta }}\cdot {\vec {E}},\gamma \,{\vec {E}}+\gamma \,{\vec {\beta }}\times {\vec {B}}\right)}$

Erhaltungssatz

Der Erhaltungssatz der elektrischen Ladung wird durch die Anwendung des konjugierten Differenzoperators auf die Quellen der Maxwellgleichung gebildet. Mit ${\displaystyle \operatorname {Skalar} (x)}$ sei hier der Real- oder Skalarteil der Quaternion ${\displaystyle x}$ bezeichnet. In den Beispielen ist ${\displaystyle x}$ ein Quaternionenprodukt.

${\displaystyle \operatorname {Skalar} \left(\left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right)\left({\vec {\nabla }}\cdot {\vec {E}},{\vec {\nabla }}\times {\vec {B}}-{\frac {\partial {\vec {E}}}{\partial t}}\right)\right)}$	${\displaystyle {=}}$	${\displaystyle \operatorname {Skalar} \left(\left({\frac {\partial }{\partial t}},-{\vec {\nabla }}\right)\,4\,\pi \left(\rho ,{\vec {J}}\right)\right)}$
${\displaystyle {\frac {\partial }{\partial t}}{\vec {\nabla }}\cdot {\vec {E}}-{\vec {\nabla }}\cdot {\frac {\partial {\vec {E}}}{\partial t}}+{\vec {\nabla }}\cdot {\vec {\nabla }}\times {\vec {B}}}$	${\displaystyle {=}}$	${\displaystyle 4\,\pi \,\left({\vec {\nabla }}\cdot {\vec {J}}+{\frac {\partial \rho }{\partial t}}\right)}$

Diese Gleichung zeigt, dass das Skalarprodukt des elektrischen Feldes ${\displaystyle {\vec {E}}}$ plus dem Kreuzprodukt des magnetischen Feldes ${\displaystyle {\vec {B}}}$ auf der einen Seite, sowie der Stromdichte ${\displaystyle {\vec {J}}}$ plus der Frequenz der Ladungsdichte ${\displaystyle \rho }$ auf der anderen Seite, gleich ist. Dieses bedeutet, dass die Ladung bei der Umformung erhalten bleibt.

Poyntings Energieerhaltungssatz wird in auf dieselbe Weise abgeleitet, mit dem Unterschied, dass statt des Differentials das konjugierte elektrische Feld ${\displaystyle {\vec {E}}}$ verwendet wird.

${\displaystyle \operatorname {Skalar} \left(\left(0,-{\vec {E}}\right)\left({\vec {\nabla }}\,{\vec {E}},{\vec {\nabla }}\times {\vec {B}}-{\frac {\partial {\vec {E}}}{\partial t}}\right)\right)}$	${\displaystyle {=}}$	${\displaystyle \operatorname {Skalar} \left(\left(0,-{\vec {E}}\right)\,4\,\pi \,\left(\rho ,{\vec {J}}\right)\right)}$
${\displaystyle {\vec {E}}\cdot {\vec {\nabla }}\times {\vec {B}}-{\vec {E}}\cdot {\frac {\partial {\vec {E}}}{\partial t}}}$	${\displaystyle {=}}$	${\displaystyle 4\,\pi {\vec {E}}\,{\vec {J}}}$

Mit d​en Vektoridentitäten

${\displaystyle {\vec {E}}\cdot \left({\vec {\nabla }}\times {\vec {B}}\right)={\vec {B}}\cdot \left({\vec {\nabla }}\times {\vec {E}}\right)+{\vec {\nabla }}\cdot \left({\vec {B}}\times {\vec {E}}\right)}$

${\displaystyle {\vec {\nabla }}\times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}$

${\displaystyle {\vec {E}}\cdot {\frac {\partial {\vec {E}}}{\partial t}}={\frac {{\left({\frac {\partial {\vec {E}}}{\partial t}}\right)}^{2}}{2}}}$

${\displaystyle {\vec {B}}\cdot {\frac {\partial {\vec {B}}}{\partial t}}={\frac {{\left({\frac {\partial {\vec {B}}}{\partial t}}\right)}^{2}}{2}}}$

kann m​an diese Gleichung nach

${\displaystyle -\left({\vec {\nabla }}\cdot \left({\vec {E}}\times {\vec {B}}\right)+{\frac {{\left(\partial {\vec {E}}+\partial {\vec {B}}\right)}^{2}}{2\,\partial t^{2}}}\right)=4\pi {\vec {E}}\cdot {\vec {J}}}$

umformen, was der Poynting-Gleichung entspricht. Der Ausdruck ${\displaystyle {\vec {E}}\times {\vec {B}}}$ entspricht hierbei dem Poynting-Vektor.

Geschichte

Gedenktafel an der Broom Bridge in Dublin, wo William Rowan Hamilton die Multiplikationsregeln im Oktober 1843 spontan in den Stein ritzte.

William Rowan Hamilton hatte 1835 die Konstruktion der komplexen Zahlen als Zahlenpaare angegeben. Dadurch motiviert, suchte er lange nach einer entsprechenden Struktur auf dem Raum ${\displaystyle \mathbb {R} ^{3}}$ der Zahlentripel; heute weiß man, dass keine derartige Struktur existiert. 1843 schließlich gelangte er zu der Erkenntnis, dass es möglich ist, eine Multiplikation auf der Menge der 4-Tupel zu konstruieren, wenn man dazu bereit ist, die Kommutativität aufzugeben. In einem Brief an seinen Sohn gibt er als Datum den 16. Oktober 1843 an und berichtet, er habe sich spontan dazu hinreißen lassen, die Multiplikationsregeln in einen Stein an der Brougham Bridge (heute Broombridge Road) in Dublin zu ritzen; später wurde dort eine Gedenktafel angebracht. Die Rechenregeln für Quaternionen waren in Ansätzen schon früher bekannt, so findet sich die Formel für den Vier-Quadrate-Satz bereits bei Leonhard Euler (1748). Andere, auch allgemeinere Multiplikationsregeln wurden von Hermann Graßmann untersucht (1855).

Schon kurz nach der Entdeckung der Quaternionen fand Hamilton die Darstellung von Drehungen des Raumes mithilfe von Quaternionen und damit eine erste Bestätigung der Bedeutung der neuen Struktur; Arthur Cayley entdeckte 1855 die entsprechenden Aussagen über orthogonale Abbildungen des vierdimensionalen Raumes. Die bloße Parametrisierung der ${\displaystyle 3\times 3}$-Drehmatrizen war hingegen schon Euler bekannt. Cayley gab 1858 in der Arbeit, in der er Matrizen einführte, auch die Möglichkeit der Darstellung von Quaternionen durch komplexe ${\displaystyle 2\times 2}$-Matrizen an.

Hamilton widmete s​ich fortan ausschließlich d​em Studium d​er Quaternionen; s​ie wurden i​n Dublin e​in eigenes Examensfach. In seiner Nachfolge w​urde 1895 s​ogar ein „Weltbund z​ur Förderung d​er Quaternionen“ gegründet. Der deutsche Mathematiker Felix Klein schreibt rückblickend über d​iese anfängliche Euphorie:

„Wie i​ch schon andeutete, schloß s​ich Hamilton e​ine Schule an, d​ie ihren Meister a​n Starrheit u​nd Intoleranz n​och überbot. […] Die Quaternionen s​ind gut u​nd brauchbar a​n ihrem Platze; s​ie reichen a​ber in i​hrer Bedeutung a​n die gewöhnlichen komplexen Zahlen n​icht heran. […] Die Leichtigkeit u​nd Eleganz, m​it der s​ich hier d​ie weittragendsten Theoreme ergeben, i​st in d​er Tat überraschend, u​nd es läßt s​ich wohl v​on hier a​us die a​lles andere ablehnende Begeisterung d​er Quaternionisten für i​hr System begreifen, d​ie […] n​un bald über vernünftige Grenzen hinauswuchs, i​n einer w​eder der Mathematik a​ls Ganzem n​och der Quaternionentheorie selbst förderlichen Weise. […] Die Verfolgung d​es angegebenen Weges – d​er neu s​ein will, obwohl e​r tatsächlich n​ur eine peinlich genaue Übertragung längst bekannter Gedanken a​uf ein einziges n​eues Objekt, a​lso durchaus k​eine geniale Konzeption bedeutet – führt z​u allerhand Erweiterungen d​er bekannten Sätze, d​ie in i​hrer Allgemeinheit d​as Hauptcharakteristikum verlieren u​nd gegenstandslos werden, allenfalls z​u Besonderheiten, d​ie ein gewisses Vergnügen gewähren mögen.“

– Felix Klein: Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert[42]

Verwandte Themen

Ähnliche Konstruktionen w​ie die Quaternionen werden manchmal u​nter dem Namen „hyperkomplexe Zahlen“ zusammengefasst. Beispielsweise s​ind die Cayley-Zahlen o​der Oktaven e​in achtdimensionales Analogon z​u den Quaternionen; i​hre Multiplikation i​st allerdings w​eder kommutativ n​och assoziativ.

Siehe auch

• Hyperkomplexe Zahl
• Spezielle unitäre Gruppe
• Quaternionische Kählermannigfaltigkeit

Literatur

• Jens Carsten Jantzen, Joachim Schwermer: Algebra. Springer, 2006, ISBN 3-540-21380-5, doi:10.1007/3-540-29287-X
• Serge Lang: Algebra. Springer-Verlag, New York 2002, ISBN 0-387-95385-X
• Max Koecher, Reinhold Remmert: Hamiltonsche Quaternionen. In: H.-D. Ebbinghaus et al.: Zahlen. Springer-Verlag, Berlin 1983, ISBN 3-540-12666-X
• John H. Conway, Derek A. Smith: On Quaternions and Octonions. A K Peters, 2003, ISBN 1-56881-134-9 (englisch)
• Jack B. Kuipers: Quaternions and Rotation Sequences. Princeton University Press, 2002, ISBN 0-691-10298-8 (englisch)
• W. Bolton: Complex Numbers (Mathematics for Engineers). Addison-Wesley, 1996, ISBN 0-582-23741-6 (englisch)
• Andrew J. Hanson: Visualizing Quaternions. Morgan Kaufmann Publishers, 2006, ISBN 0-12-088400-3 (englisch)
• Lew Semjonowitsch Pontrjagin: Verallgemeinerungen der Zahlen. Verlag Harri Deutsch, 1995
• S. Eilenberg, I. Niven: The „fundamental theorem of algebra“ for quaternions. In: Bull. Amer. Soc., 50, 1944, S. 246–248.
• Hölder: Bemerkung zur Quaternionentheorie (Wikisource)

Weblinks

• Doing Physics with Quaternions (PDF; 563 kB)
• Tsit Yuen Lam (Berkeley): Hamilton’s Quaternions (PostScript, englisch). Abgerufen am 30. August 2009.
• Quaternionen in der Computeranimation
• Der Ort der Entdeckung der Quaternionen (mit Bildern)
• Eric W. Weisstein: Quaternion. In: MathWorld (englisch).
• What are quaternions, and how do you visualize them? A story of four dimensions. auf YouTube
• Was sind und was sollen die Quaternionen? auf YouTube von Edmund Weitz

Einzelnachweise und Anmerkungen

1. Albrecht Beutelspacher: Lineare Algebra. 7. Auflage. Vieweg+Teubner Verlag, Wiesbaden 2010, ISBN 978-3-528-66508-1, S. 30.
2. Bei Gauß findet sich eine Notiz über die Multiplikation und Konjugation von Quadrupeln im Kapitel Mutation des Raumes. In: Carl Friedrich Gauß: Werke. Achter Band. König. Gesell. Wissen., Göttingen 1900, S. 357–361, die auf das Jahr 1819 datiert wird. Die Unterschiede zu Hamilton gehen nicht über notationelle Konventionen hinaus. (Zitiert nach Lam S. 25).
3. Lam S. 1
4. Karsten Kunze, Helmut Schaeben: The Bingham Distribution of Quaternions und Its Spherical Radon Transform in Texture Analysis. In: Mathematical Geology. 8, November 2004, S. 917–943. doi:10.1023/B:MATG.0000048799.56445.59.
5. Sie ist nicht mit dem Skalarprodukt zu verwechseln.
6. die wegen der fehlenden Kommutativität in der Multiplikation nicht automatisch auf eines reduziert werden können.
7. NB: ${\displaystyle {\vec {x}}}$ wird bei Bedarf genauso als Spaltenvektor eingesetzt.
8. Reelle Faktoren kommutieren mit ${\displaystyle \mathrm {i} ,\mathrm {j} ,\mathrm {k} }$ und damit mit allen Quaternionen, d. h. es gilt beispielsweise

   ${\displaystyle 2\mathrm {i} \mathrm {j} =\mathrm {i} 2\mathrm {j} =\mathrm {i} \mathrm {j} 2=2\mathrm {k} ,}$

   aber

   ${\displaystyle 2\mathrm {j} \mathrm {i} =\mathrm {j} 2\mathrm {i} =\mathrm {j} \mathrm {i} 2=-2\mathrm {k} .}$

   Nicht alle aus der elementaren Algebra bekannten Rechenregeln gelten für die Quaternionen, z. B. gilt

   ${\displaystyle (\mathrm {i} +\mathrm {j} )(\mathrm {i} -\mathrm {j} )=\mathrm {i} \mathrm {i} -\mathrm {i} \mathrm {j} +\mathrm {j} \mathrm {i} -\mathrm {j} \mathrm {j} =(-1)-\mathrm {k} +(-\mathrm {k} )-(-1)=-2\mathrm {k} .}$

   Die binomischen Formeln ${\displaystyle (a+b)(a-b)=a^{2}-b^{2}}$ oder ${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ sind hier also nicht anwendbar. Sie setzen voraus, dass ${\displaystyle ab=ba}$ gilt.
9. Im Komplexen gilt dagegen

   ${\displaystyle \operatorname {Im} \,z={\frac {1}{2\mathrm {i} _{\mathbb {C} }}}(z-{\bar {z}})}$

   mit Abspaltung der imaginären Einheit ${\displaystyle \mathrm {i} _{\mathbb {C} }}$ von der rein-imaginären Komponente, so dass der Imaginärteil eine reelle Zahl ist. Und es gilt:

   ${\displaystyle z=\operatorname {Re} \,z+\mathrm {i} _{\mathbb {C} }\;\operatorname {Im} \,z.}$

10. und damit auch Betrag und die Teilmenge der reellen Zahlen. Bei den komplexen Zahlen gilt dies nicht (s. a. Komplexe Zahl#Körpertheorie und algebraische Geometrie).
11. Viele Autoren setzen jedoch Norm dem Betrag gleich.
12. Den unendlich vielen Nullstellen des Polynoms ${\displaystyle X^{2}+1}$ steht das Fehlen einer Nullstelle beim Polynom ${\displaystyle \mathrm {i} X-X\mathrm {i} +1}$ vom Grad 1 gegenüber. Letzteres besitzt 2 Monome vom Grad 1, dem höchsten Grad seiner Monome. In nicht-kommutativen Ringen wird der Grad des Monoms ${\displaystyle a_{0}Xa_{1}\dots a_{n-1}Xa_{n}}$ mit ${\displaystyle a_{i}\neq 0}$ zu ${\displaystyle n}$ definiert, und ein Monom dominiert ein Polynom, wenn es unter allen Monomen den höchsten Grad hat. Dann ist der Grad des Polynoms auch gleich dem Grad der dominierenden Monome. Hat ein Polynom über ${\displaystyle \mathbb {H} }$ ein einziges dominierendes Monom von einem Grad > 0, dann hat es immer eine Nullstelle in ${\displaystyle \mathbb {H} }$. (Eilenberg-Niven).
13. John H. Conway, Derek A. Smith: On Quaternions and Octonions. A K Peters, 2003, ISBN 1-56881-134-9 (englisch).
14. Ein Automorphismus definiert eine solche Einbettung (durch Einschränkung), die nur eine Einbettung von ${\displaystyle \mathbb {R} }$-Algebren ist. ${\displaystyle \mathbb {H} }$ ist keine Algebra über ${\displaystyle \mathbb {C} }$.
15. Tsit Yuen Lam (Berkeley): Hamilton’s Quaternions (PostScript, englisch). Abgerufen am 30. August 2009, Seite 22. Der Polarwinkel ist das Analogon zum komplexen Argument ${\displaystyle \operatorname {arg} (z)}$, allerdings ist bei dessen Hauptwert das Signum des Imaginärteils mit hinein genommen, was sich bei den Quaternionen nicht machen lässt, so dass ${\displaystyle \operatorname {arg} }$ nicht eine einfache Einschränkung des Polarwinkels ist.
16. Für ${\displaystyle x^{\prime }:=\mathrm {i} \pi }$ und ${\displaystyle y^{\prime }:=\mathrm {j} \pi }$ ist

    ${\displaystyle \exp x^{\prime }\exp y^{\prime }=\exp(\mathrm {i} \pi )\exp(\mathrm {j} \pi )=(-1)(-1)=1}$

    ${\displaystyle \neq \exp(x^{\prime }+y^{\prime })=\exp((\mathrm {i} +\mathrm {j} )\pi )=\cos(\pi {\sqrt {2}})+{\frac {\mathrm {i} +\mathrm {j} }{\sqrt {2}}}\sin(\pi {\sqrt {2}})}$.

17. Laut Tsit Yuen Lam (Berkeley): Hamilton’s Quaternions (PostScript, englisch). Abgerufen am 30. August 2009, Seite 22 mag das Scheitern dieser Funktionalgleichung das größte Hindernis für eine quaternionische Funktionentheorie gewesen sein.
18. Lce.hut.fi (PDF; 68 kB)
19. Die Überlegungen gelten schon, wenn der Definitionsbereich von ${\displaystyle g}$ ein Gebiet ist.
20. en:Quaternion variable (englisch).
21. Letzteres ist aber nicht hinreichend, denn die Funktion ${\displaystyle g(z):=\operatorname {Im} z}$ ist trotz ${\displaystyle g\!\mid _{\mathbb {R} }\,=0\in \mathbb {R} }$ wegen ${\displaystyle u(\xi ,\eta )\equiv \eta \not \equiv -\eta \equiv u(\xi ,-\eta )}$ nicht einbettbar.
    Sind jedoch bei solchen Funktionen die Cauchy-Riemannschen Differentialgleichungen erfüllt, so folgt aus der Ungeradheit von ${\displaystyle v(\xi ,\eta )}$ die Geradheit von ${\displaystyle u(\xi ,\eta )}$ (jeweils in der zweiten Variablen) und damit die Einbettbarkeit in die Quaternionen.
    Im Gegensatz zu ${\displaystyle g(z)=\operatorname {Im} z}$ ist die Funktion ${\displaystyle h(z):=\mathrm {i} _{\mathbb {C} }\,\operatorname {Im} z}$ einbettbar mit der Fortsetzung ${\displaystyle {\tilde {h}}\colon \mathbb {H} \to \mathbb {H} ;q\mapsto \operatorname {Im} q.}$
22. Ein weiteres nicht einbettbares Beispiel ist ${\displaystyle g(z):=\mathrm {i} _{\mathbb {C} }}$, bei dem ${\displaystyle v(\xi ,\eta )=1}$ nicht ungerade ist in ${\displaystyle \eta }$. Die Einbettung mithilfe des Einbettungsisomorphismus ${\displaystyle \iota _{{\mathrm {i} }_{\mathbb {H} }}}$ ergibt zwar die (konstante) Funktion ${\displaystyle g_{{\mathrm {i} }_{\mathbb {H} }}=\mathrm {i} _{\mathbb {H} }}$, die aber mit anderen Einbettungen, z. B. ${\displaystyle \iota _{{\mathrm {j} }_{\mathbb {H} }}}$ mit dem (ebenfalls konstanten) Ergebnis ${\displaystyle g_{{\mathrm {j} }_{\mathbb {H} }}=\mathrm {j} _{\mathbb {H} }\neq \mathrm {i} _{\mathbb {H} },}$ nicht zusammenpasst.
23. Quaternion Analysis, Functions of a Quaternion Variable (englisch).
24. R. Fueter: Über die analytische Darstellung der regulären Funktionen einer Quaternionenvariablen. In: Comm. Math. Helv.. 8, 1936, S. 371–378.
25. C.A. Deavours: The Quaternion Calculus. In: Amer. Math. Monthly. 80, 1973, S. 995–1008. (englisch)
26. A. Sudbery: Quaternionic Analysis. In: Math. Proc. Camb. Phil. Soc.. 85, 1979, S. 199–225. doi:10.1017/S0305004100055638. (englisch)
27. zu ${\displaystyle \mathrm {SO} (3)}$ siehe Orthogonale Gruppe#Räumliche Drehung.
28. Zur Komplexität, Mehrdeutigkeit und zum Phänomen des „Gimbal Lock“ siehe en:Rotation matrix#Euler angles.
29. Wie im referenzierten Abschnitt und im Abschnitt #Automorphismen bemerkt, gibt es zu jedem fixen Dreibein ${\displaystyle \mathrm {i} ,\mathrm {j} ,\mathrm {k} }$ sehr viele verschiedene Einbettungen dieser endlichen Untergruppen in ${\displaystyle \mathbb {H} }$.
30. Diese Gruppen firmieren – besonders in der englischen Literatur – auch als binäre Erweiterung ${\displaystyle \mathrm {2P} }$ der Polyedergruppe ${\displaystyle \mathrm {P} }$, und die binären Diedergruppen ${\displaystyle \mathrm {2D} _{n}}$ zusätzlich als verallgemeinerte Quaternionengruppen, auch als dizyklische Gruppen, in Zeichen ${\displaystyle \mathrm {Dic} _{n}}$.
31. Gabor Gévay: On Perfect 4-Polytopes (PDF; 211 kB) Contributions to Algebra and Geometry Volume 43 (2002), No. 1, 243–259: gibt auf S. 256 die 4-Polytope »${\displaystyle \{2p\}\Box \{2p\}}$« für die ${\displaystyle \mathrm {2D} _{p}}$ bzw. auf S. 252 Table 2 das 4-Polytop »${\displaystyle {\text{f}}_{1,2}{\text{F}}_{4}}$« für ${\displaystyle \mathrm {2O} }$.
32. Tsit Yuen Lam (Berkeley): Hamilton’s Quaternions (PostScript, englisch). Abgerufen am 30. August 2009, Seite 24
33. Eric W. Weisstein: Antihomomorphism. In: MathWorld (englisch).
34. ein ${\displaystyle \mathbb {R} }$-Vektorraum, der aber weder ${\displaystyle \mathbb {C} ^{2\times 2}}$-Ideal noch ${\displaystyle \mathbb {C} }$-Vektorraum ist, da   ${\displaystyle \mathrm {i} _{\mathbb {C} }\,1_{H}\notin H}$
35. Die Matrizen ${\displaystyle \mathrm {i} _{H},\mathrm {j} _{H},\mathrm {k} _{H}}$ sind spurfrei und schiefhermitesch.
36. Nur Matrixringe der Dimensionen 1, 2 und 4 über ${\displaystyle \mathbb {R} }$ sind nullteilerfrei (siehe auch #Die Quaternionen als Algebra).
37. Diese Möglichkeiten entsprechen der Vorschaltung eines Automorphismus.
38. Satz von Frobenius (reelle Divisionsalgebren) (en:Frobenius theorem (real division algebras)) Corollary 6.8 in Chapter iX von Hungerford: Algebra (Springer 1974).
39. Satz von Hurwitz (normierte Divisionsalgebren) (en:Hurwitz's theorem (normed division algebras)).
40. Satz von Pontrjagin (1931) in Pontrjagin: Jeder lokalkompakte, zusammenhängende topologische Schiefkörper ist entweder der Körper der reellen Zahlen oder der Körper der komplexen Zahlen oder der Schiefkörper der Quaternionen.
41. Die Beispiele haben als ersten Operanden ${\displaystyle x}$ alle einen Differentialoperator, der auf den zweiten Operanden ${\displaystyle y}$ wirkt. Die Brüche enthalten jedoch mit ${\displaystyle y\,x}$ eine unbrauchbare Reihenfolge. Bei den Ausrechnungen ganz rechts kommt immer ${\displaystyle x}$ vor ${\displaystyle y}$.
42. Felix Klein: Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. Teil I. Verlag von Julius Springer, Berlin 1926, S. 184 ff.