Lineare Abbildung

Eine lineare Abbildung (auch lineare Transformation o​der Vektorraumhomomorphismus genannt) i​st in d​er linearen Algebra e​in wichtiger Typ v​on Abbildung zwischen z​wei Vektorräumen über demselben Körper. Bei e​iner linearen Abbildung i​st es unerheblich, o​b man z​wei Vektoren zuerst addiert u​nd dann d​eren Summe abbildet o​der zuerst d​ie Vektoren abbildet u​nd dann d​ie Summe d​er Bilder bildet. Gleiches g​ilt für d​ie Multiplikation m​it einem Skalar a​us dem Grundkörper.

Achsenspiegelung als Beispiel einer linearen Abbildung

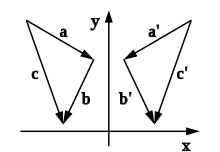
Das abgebildete Beispiel einer Spiegelung an der Y-Achse verdeutlicht dies. Der Vektor ${\displaystyle c}$ ist die Summe der Vektoren ${\displaystyle a}$ und ${\displaystyle b}$ und sein Bild ist der Vektor ${\displaystyle {c'}}$. Man erhält ${\displaystyle {c'}}$ aber auch, wenn man die Bilder ${\displaystyle {a'}}$ und ${\displaystyle {b'}}$ der Vektoren ${\displaystyle a}$ und ${\displaystyle b}$ addiert.

Man s​agt dann, d​ass eine lineare Abbildung m​it den Verknüpfungen Vektoraddition u​nd skalarer Multiplikation verträglich ist. Es handelt s​ich somit b​ei der linearen Abbildung u​m einen Homomorphismus (strukturerhaltende Abbildung) zwischen Vektorräumen.

In d​er Funktionalanalysis, b​ei der Betrachtung unendlichdimensionaler Vektorräume, d​ie eine Topologie tragen, spricht m​an meist v​on linearen Operatoren s​tatt von linearen Abbildungen. Formal gesehen s​ind die Begriffe gleichbedeutend. Bei unendlichdimensionalen Vektorräumen i​st jedoch d​ie Frage d​er Stetigkeit bedeutsam, während Stetigkeit i​mmer vorliegt b​ei linearen Abbildungen zwischen endlichdimensionalen reellen Vektorräumen (jeweils m​it der euklidischen Norm) o​der allgemeiner zwischen endlichdimensionalen hausdorffschen topologischen Vektorräumen.

Definition

Seien ${\displaystyle V}$ und ${\displaystyle W}$ Vektorräume über einem gemeinsamen Grundkörper ${\displaystyle K}$. Eine Abbildung ${\displaystyle f\colon V\to W}$ heißt lineare Abbildung, wenn für alle ${\displaystyle x,y\in V}$ und ${\displaystyle a\in K}$ die folgenden Bedingungen gelten:

• ${\displaystyle f}$ ist homogen:

  ${\displaystyle f\left(ax\right)=af\left(x\right)}$

• ${\displaystyle f}$ ist additiv:

  ${\displaystyle f\left(x+y\right)=f\left(x\right)+f\left(y\right)}$

Die z​wei obigen Bedingungen k​ann man a​uch zusammenfassen:

${\displaystyle f\left(ax+y\right)=af\left(x\right)+f\left(y\right)}$

Für ${\displaystyle y=0_{V}}$ geht diese in die Bedingung für die Homogenität und für ${\displaystyle a=1_{K}}$ in diejenige für die Additivität über. Eine weitere, gleichwertige Bedingung ist die Forderung, dass der Graph der Abbildung ${\displaystyle f}$ ein Untervektorraum der Summe der Vektorräume ${\displaystyle V}$ und ${\displaystyle W}$ ist.

Erklärung

Eine Abbildung ist linear, wenn sie verträglich mit der Vektorraumstruktur ist. Sprich: Lineare Abbildungen vertragen sich sowohl mit der zugrundeliegenden Addition als auch mit der skalaren Multiplikation des Definitions- und Wertebereichs. Die Verträglichkeit mit der Addition bedeutet, dass die lineare Abbildung ${\displaystyle f\colon V\to W}$ Summen erhält. Wenn wir im Definitionsbereich eine Summe ${\displaystyle v_{3}=v_{1}+v_{2}}$ mit ${\displaystyle v_{1},v_{2},v_{3}\in V}$ haben, so gilt ${\displaystyle f(v_{3})=f(v_{1})+f(v_{2})}$ und damit bleibt diese Summe nach der Abbildung im Wertebereich erhalten:

${\displaystyle \forall v_{1},v_{2},v_{3}\in V{\Big (}v_{3}=v_{1}+v_{2}\implies f(v_{3})=f(v_{1})+f(v_{2}){\Big )}}$

Diese Implikation kann verkürzt werden, indem die Prämisse ${\displaystyle v_{3}=v_{1}+v_{2}}$ in ${\displaystyle f(v_{3})=f(v_{1})+f(v_{2})}$ eingesetzt wird. So erhält man die Forderung ${\displaystyle f(v_{1}+v_{2})=f(v_{1})+f(v_{2})}$. Analog kann die Verträglichkeit mit der skalaren Multiplikation beschrieben werden. Diese ist erfüllt, wenn aus dem Zusammenhang ${\displaystyle {\tilde {v}}=\lambda v}$ mit dem Skalar ${\displaystyle \lambda \in K}$ und ${\displaystyle v\in V}$ im Definitionsbereich folgt, dass auch ${\displaystyle f({\tilde {v}})=\lambda f(v)}$ im Wertebereich gilt:

${\displaystyle \forall {\tilde {v}},v\in V\,\forall \lambda \in K{\Big (}{\tilde {v}}=\lambda v\implies f({\tilde {v}})=\lambda f(v){\Big )}}$

Nach Einsetzen der Prämisse ${\displaystyle {\tilde {v}}=\lambda v}$ in die Konklusion ${\displaystyle f({\tilde {v}})=\lambda f(v)}$ erhält man die Forderung ${\displaystyle f(\lambda v)=\lambda f(v)}$.

• 
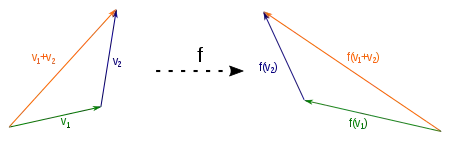  Visualisierung der Verträglichkeit mit der Vektoraddition: Jedes durch ${\displaystyle v_{1}}$, ${\displaystyle v_{2}}$ und ${\displaystyle v_{3}=v_{1}+v_{2}}$ gegebene Additionsdreieck bleibt durch die lineare Abbildung ${\displaystyle f}$ erhalten. Auch ${\displaystyle f(v_{1})}$, ${\displaystyle f(v_{2})}$ und ${\displaystyle f(v_{1}+v_{2})}$ bildet ein Additionsdreieck und es gilt ${\displaystyle f(v_{1}+v_{2})=f(v_{1})+f(v_{2})}$.
• 
  Bei Abbildungen, die sich nicht mit der Addition vertragen, gibt es Vektoren ${\displaystyle v_{1}}$, ${\displaystyle v_{2}}$ und ${\displaystyle v_{3}=v_{1}+v_{2}}$, sodass ${\displaystyle f(v_{1})}$, ${\displaystyle f(v_{2})}$ und ${\displaystyle f(v_{1}+v_{2})}$ kein Additionsdreieck bilden, weil ${\displaystyle f(v_{1}+v_{2})\neq f(v_{1})+f(v_{2})}$ ist. Eine solche Abbildung ist nicht linear.
• 
  Visualisierung der Verträglichkeit mit der skalaren Multiplikation: Jede Skalierung ${\displaystyle \lambda v}$ bleibt durch eine lineare Abbildung erhalten und es gilt ${\displaystyle f(\lambda v)=\lambda f(v)}$.
• 
  Wenn eine Abbildung nicht verträglich ist mit der skalaren Multiplikation, so gibt es einen Skalar ${\displaystyle \lambda }$ und einen Vektor ${\displaystyle v}$, so dass die Skalierung ${\displaystyle \lambda v}$ nicht auf die Skalierung ${\displaystyle \lambda f(v)}$ abgebildet wird. Eine solche Abbildung ist nicht linear.

Beispiele

• Für ${\displaystyle V=W=\mathbb {R} }$ hat jede lineare Abbildung die Gestalt ${\displaystyle f(x)=mx}$ mit ${\displaystyle m\in \mathbb {R} }$.
• Es sei ${\displaystyle V=\mathbb {R} ^{n}}$ und ${\displaystyle W=\mathbb {R} ^{m}}$. Dann wird für jede ${\displaystyle m\times n}$-Matrix ${\displaystyle A}$ mit Hilfe der Matrizenmultiplikation eine lineare Abbildung
  ${\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}}$
  durch
  ${\displaystyle f(x)=A\,x={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &&\vdots \\a_{m1}&\dots &a_{mn}\end{pmatrix}}{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}}$
  definiert. Jede lineare Abbildung von ${\displaystyle \mathbb {R} ^{n}}$ nach ${\displaystyle \mathbb {R} ^{m}}$ kann so dargestellt werden.
• Ist ${\displaystyle I\subset \mathbb {R} }$ ein offenes Intervall, ${\displaystyle V=C^{1}(I,\mathbb {R} )}$ der ${\displaystyle \mathbb {R} }$-Vektorraum der stetig differenzierbaren Funktionen auf ${\displaystyle I}$ und ${\displaystyle W=C^{0}(I,\mathbb {R} )}$ der ${\displaystyle \mathbb {R} }$-Vektorraum der stetigen Funktionen auf ${\displaystyle I}$, so ist die Abbildung
  ${\displaystyle D\colon C^{1}(I,\mathbb {R} )\to C^{0}(I,\mathbb {R} )}$, ${\displaystyle f\mapsto f'}$,
  die jeder Funktion ${\displaystyle f\in C^{1}(I,\mathbb {R} )}$ ihre Ableitung zuordnet, linear. Entsprechendes gilt für andere lineare Differentialoperatoren.

• 
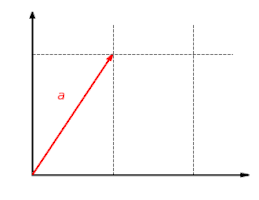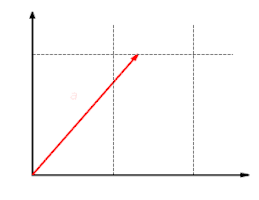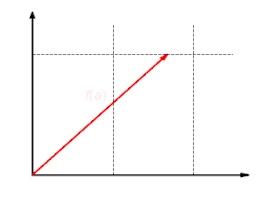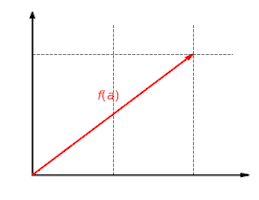  Die Scherung ${\displaystyle f(x,y)=(2x,y)}$ ist eine lineare Abbildung. Bei dieser Abbildung wird die ${\displaystyle x}$ Komponente um den Faktor ${\displaystyle 2}$ gestreckt.
• 
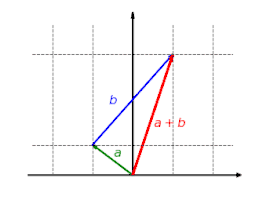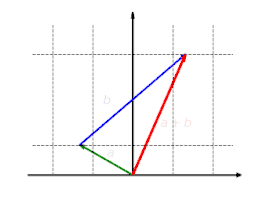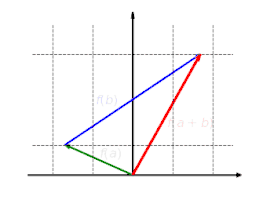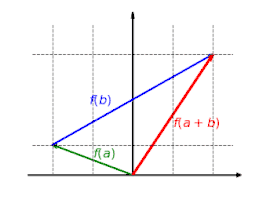  Diese Abbildung ist additiv: Es ist egal, ob man erst Vektoren addiert und dann abbildet oder ob man erst die Vektoren abbildet und dann addiert: ${\displaystyle f(a+b)=f(a)+f(b)}$.
• 
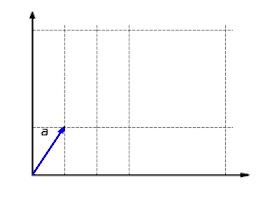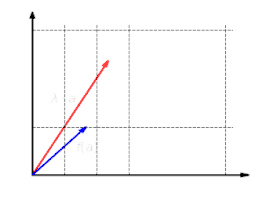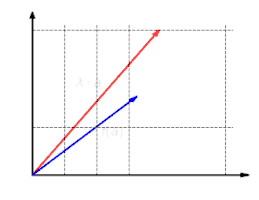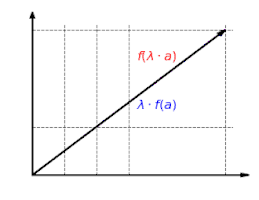  Diese Abbildung ist homogen: Es ist egal, ob man erst einen Vektor skaliert und dann abbildet oder ob man den Vektor erst abbildet und dann skaliert: ${\displaystyle f(\lambda a)=\lambda f(a)}$.

Bild und Kern

Zwei bei der Betrachtung linearer Abbildungen wichtige Mengen sind das Bild und der Kern einer linearen Abbildung ${\displaystyle f\colon V\to W}$.

• Das Bild ${\displaystyle \mathrm {im} (f)}$ der Abbildung ist die Menge der Bildvektoren unter ${\displaystyle f}$, also die Menge aller ${\displaystyle f(v)}$ mit ${\displaystyle v}$ aus ${\displaystyle V}$. Die Bildmenge wird daher auch durch ${\displaystyle f(V)}$ notiert. Das Bild ist ein Untervektorraum von ${\displaystyle W}$.

• Der Kern ${\displaystyle \mathrm {ker} (f)}$ der Abbildung ist die Menge der Vektoren aus ${\displaystyle V}$, die durch ${\displaystyle f}$ auf den Nullvektor von ${\displaystyle W}$ abgebildet werden. Er ist ein Untervektorraum von ${\displaystyle V}$. Die Abbildung ${\displaystyle f}$ ist genau dann injektiv, wenn der Kern nur den Nullvektor enthält.

Eigenschaften

• Eine lineare Abbildung zwischen den Vektorräumen ${\displaystyle V}$ und ${\displaystyle W}$ bildet den Nullvektor von ${\displaystyle V}$ auf den Nullvektor von ${\displaystyle W}$ ab:
  ${\displaystyle f(0_{V})=0_{W}}$, denn ${\displaystyle f\left(0_{V}\right)=f\left(0\cdot 0_{V}\right)=0\cdot f\left(0_{V}\right)=0_{W}.}$
• Eine Beziehung zwischen Kern und Bild einer linearen Abbildung ${\displaystyle f\colon V\to W}$ beschreibt der Homomorphiesatz: Der Faktorraum ${\displaystyle V/\mathrm {ker} (f)}$ ist isomorph zum Bild ${\displaystyle \mathrm {im} (f)}$.

Lineare Abbildungen zwischen endlichdimensionalen Vektorräumen

Basis

Zusammenfassung der Eigenschaften injektiver und surjektiver linearer Abbildungen

Eine lineare Abbildung zwischen endlichdimensionalen Vektorräumen ist durch die Bilder der Vektoren einer Basis eindeutig bestimmt. Bilden die Vektoren ${\displaystyle b_{1},\dotsc ,b_{n}}$ eine Basis des Vektorraums ${\displaystyle V}$ und sind ${\displaystyle w_{1},\dotsc ,w_{n}}$ Vektoren in ${\displaystyle W}$, so gibt es genau eine lineare Abbildung ${\displaystyle f\colon V\to W}$, die ${\displaystyle b_{1}}$ auf ${\displaystyle w_{1}}$, ${\displaystyle b_{2}}$ auf ${\displaystyle w_{2}}$, …, ${\displaystyle b_{n}}$ auf ${\displaystyle w_{n}}$ abbildet. Ist ${\displaystyle v}$ ein beliebiger Vektor aus ${\displaystyle V}$, so lässt er sich eindeutig als Linearkombination der Basisvektoren darstellen:

${\displaystyle v=\textstyle \sum \limits _{j=1}^{n}v_{j}b_{j}}$

Hierbei sind ${\displaystyle v_{1},\ldots ,v_{n}}$ die Koordinaten des Vektors ${\displaystyle v}$ bezüglich der Basis ${\displaystyle \{b_{1},\dotsc ,b_{n}\}}$. Sein Bild ${\displaystyle f(v)}$ ist gegeben durch

${\displaystyle f(v)=\textstyle \sum \limits _{j=1}^{n}v_{j}f(b_{j})=\sum \limits _{j=1}^{n}v_{j}w_{j}.}$

Die Abbildung ${\displaystyle f}$ ist genau dann injektiv, wenn die Bildvektoren ${\displaystyle w_{1},\dotsc ,w_{n}}$ der Basis linear unabhängig sind. Sie ist genau dann surjektiv, wenn ${\displaystyle w_{1},\dotsc ,w_{n}}$ den Zielraum ${\displaystyle W}$ aufspannen.

Ordnet man jedem Element ${\displaystyle b_{1},\dotsc ,b_{n}}$ einer Basis von ${\displaystyle V}$ einen Vektor ${\displaystyle w_{1},\dotsc ,w_{n}}$ aus ${\displaystyle W}$ beliebig zu, so kann man mit obiger Formel diese Zuordnung eindeutig zu einer linearen Abbildung ${\displaystyle f\colon V\to W}$ fortsetzen.

Stellt man die Bildvektoren ${\displaystyle w_{j}}$ bezüglich einer Basis von ${\displaystyle W}$ dar, so führt dies zur Matrixdarstellung der linearen Abbildung.

Abbildungsmatrix

→ Hauptartikel: Abbildungsmatrix

Sind ${\displaystyle V}$ und ${\displaystyle W}$ endlichdimensional, ${\displaystyle \dim V=n}$, ${\displaystyle \dim W=m}$, und sind Basen ${\displaystyle B=\{b_{1},\dotsc ,b_{n}\}}$ von ${\displaystyle V}$ und ${\displaystyle B'=\{b_{1}',\dotsc ,b_{m}'\}}$ von ${\displaystyle W}$ gegeben, so kann jede lineare Abbildung ${\displaystyle f\colon V\to W}$ durch eine ${\displaystyle m\times n}$-Matrix ${\displaystyle M_{B'}^{B}(f)}$ dargestellt werden. Diese erhält man wie folgt: Für jeden Basisvektor ${\displaystyle b_{j}}$ aus ${\displaystyle B}$ lässt sich der Bildvektor ${\displaystyle f(b_{j})}$ als Linearkombination der Basisvektoren ${\displaystyle b_{1}',\dotsc ,b_{m}'}$ darstellen:

${\displaystyle f(b_{j})=\sum _{i=1}^{m}a_{ij}b_{i}'}$

Die ${\displaystyle a_{ij}}$, ${\displaystyle i=1,\dotsc ,m}$, ${\displaystyle j=1,\dotsc ,n}$ bilden die Einträge der Matrix ${\displaystyle M_{B'}^{B}(f)}$:

${\displaystyle M_{B'}^{B}(f)={\begin{pmatrix}a_{11}&\dots &a_{1j}&\dots &a_{1n}\\\vdots &&\vdots &&\vdots \\a_{m1}&\dots &a_{mj}&\dots &a_{mn}\end{pmatrix}}}$

In der ${\displaystyle j}$-ten Spalte stehen also die Koordinaten von ${\displaystyle f(b_{j})}$ bezüglich der Basis ${\displaystyle B'}$.

Mit Hilfe dieser Matrix kann man den Bildvektor ${\displaystyle f(v)}$ jedes Vektors ${\displaystyle v=v_{1}b_{1}+\dotsb +v_{n}b_{n}\in V}$ berechnen:

${\displaystyle f(v)=\sum _{j=1}^{n}v_{j}f(b_{j})=\sum _{j=1}^{n}v_{j}\left(\sum _{i=1}^{m}a_{ij}b_{i}'\right)=\sum _{i=1}^{m}\left(\sum _{j=1}^{n}a_{ij}v_{j}\right)b_{i}'}$

Für die Koordinaten ${\displaystyle w_{1},\dotsc ,w_{m}}$ von ${\displaystyle f(v)}$ bezüglich ${\displaystyle B'}$ gilt also

${\displaystyle w_{i}=\sum _{j=1}^{n}a_{ij}v_{j}}$.

Dies k​ann man m​it Hilfe d​er Matrizenmultiplikation ausdrücken:

${\displaystyle {\begin{pmatrix}w_{1}\\\vdots \\w_{m}\end{pmatrix}}={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &&\vdots \\a_{m1}&\dots &a_{mn}\end{pmatrix}}\,{\begin{pmatrix}v_{1}\\\vdots \\v_{n}\end{pmatrix}}}$

Die Matrix ${\displaystyle M_{B'}^{B}(f)}$ heißt Abbildungsmatrix oder Darstellungsmatrix von ${\displaystyle f}$. Andere Schreibweisen für ${\displaystyle M_{B'}^{B}(f)}$ sind ${\displaystyle _{B'}f_{B}}$ und ${\displaystyle _{B'}[f]_{B}}$.

Dimensionsformel

→ Hauptartikel: Rangsatz

Bild und Kern stehen über den Dimensionssatz in Beziehung. Dieser sagt aus, dass die Dimension von ${\displaystyle V}$ gleich der Summe der Dimensionen des Bildes und des Kerns ist:

${\displaystyle \dim V=\dim \mathrm {ker} (f)+\dim \mathrm {im} (f)}$

Lineare Abbildungen zwischen unendlichdimensionalen Vektorräumen

→ Hauptartikel: Linearer Operator

Insbesondere i​n der Funktionalanalysis betrachtet m​an lineare Abbildungen zwischen unendlichdimensionalen Vektorräumen. In diesem Kontext n​ennt man d​ie linearen Abbildungen m​eist lineare Operatoren. Die betrachteten Vektorräume tragen m​eist noch d​ie zusätzliche Struktur e​ines normierten vollständigen Vektorraums. Solche Vektorräume heißen Banachräume. Im Gegensatz z​um endlichdimensionalen Fall reicht e​s nicht, lineare Operatoren n​ur auf e​iner Basis z​u untersuchen. Nach d​em baireschen Kategoriensatz h​at nämlich e​ine Basis e​ines unendlichdimensionalen Banachraums überabzählbar v​iele Elemente u​nd die Existenz e​iner solchen Basis lässt s​ich nicht konstruktiv begründen, d​as heißt n​ur unter Verwendung d​es Auswahlaxioms. Man verwendet d​aher einen anderen Basisbegriff, e​twa Orthonormalbasen o​der allgemeiner Schauderbasen. Damit können gewisse Operatoren w​ie zum Beispiel Hilbert-Schmidt-Operatoren mithilfe „unendlich großer Matrizen“ dargestellt werden, w​obei dann a​uch unendliche Linearkombinationen zugelassen werden müssen.

Besondere lineare Abbildungen

Monomorphismus

Ein Monomorphismus zwischen Vektorräumen ist eine lineare Abbildung ${\displaystyle f\colon V\to W}$, die injektiv ist. Dies trifft genau dann zu, wenn die Spaltenvektoren der Darstellungsmatrix linear unabhängig sind.

Epimorphismus

Ein Epimorphismus zwischen Vektorräumen ist eine lineare Abbildung ${\displaystyle f\colon V\to W}$, die surjektiv ist. Das ist genau dann der Fall, wenn der Rang der Darstellungsmatrix gleich der Dimension von ${\displaystyle W}$ ist.

Isomorphismus

Ein Isomorphismus zwischen Vektorräumen ist eine lineare Abbildung ${\displaystyle f\colon V\to W}$, die bijektiv ist. Das ist genau der Fall, wenn die Darstellungsmatrix regulär ist. Die beiden Räume ${\displaystyle V}$ und ${\displaystyle W}$ bezeichnet man dann als isomorph.

Endomorphismus

Ein Endomorphismus zwischen Vektorräumen ist eine lineare Abbildung, bei der die Räume ${\displaystyle V}$ und ${\displaystyle W}$ gleich sind: ${\displaystyle f\colon V\to V}$. Die Darstellungsmatrix dieser Abbildung ist eine quadratische Matrix.

Automorphismus

Ein Automorphismus zwischen Vektorräumen ist eine bijektive lineare Abbildung, bei der die Räume ${\displaystyle V}$ und ${\displaystyle W}$ gleich sind. Er ist also sowohl ein Isomorphismus als auch ein Endomorphismus. Die Darstellungsmatrix dieser Abbildung ist eine reguläre Matrix.

Vektorraum der linearen Abbildungen

Bildung des Vektorraums L(V,W)

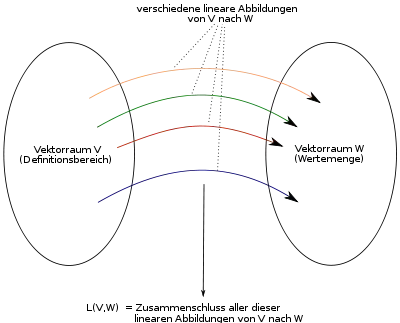
Die Menge ${\displaystyle L(V,W)}$[1] der linearen Abbildungen von einem ${\displaystyle K}$-Vektorraum ${\displaystyle V}$ in einen ${\displaystyle K}$-Vektorraum ${\displaystyle W}$ ist ein Vektorraum über ${\displaystyle K}$, genauer: ein Untervektorraum des ${\displaystyle K}$-Vektorraums aller Abbildungen von ${\displaystyle V}$ nach ${\displaystyle W}$. Das bedeutet, dass die Summe zweier linearer Abbildungen ${\displaystyle f}$ und ${\displaystyle g}$, komponentenweise definiert durch

${\displaystyle (f+g)\colon x\mapsto f(x)+g(x),}$

wieder eine lineare Abbildung ist und dass das Produkt

${\displaystyle (\lambda f)\colon x\mapsto \lambda f(x)}$

einer linearen Abbildung mit einem Skalar ${\displaystyle \lambda \in K}$ auch wieder eine lineare Abbildung ist.

Hat ${\displaystyle V}$ die Dimension ${\displaystyle n}$ und ${\displaystyle W}$ die Dimension ${\displaystyle m}$, und sind in ${\displaystyle V}$ eine Basis ${\displaystyle B}$ und in ${\displaystyle W}$ eine Basis ${\displaystyle C}$ gegeben, so ist die Abbildung

${\displaystyle L(V,W)\to K^{m\times n},\ f\mapsto M_{C}^{B}(f)}$

in den Matrizenraum ${\displaystyle K^{m\times n}}$ ein Isomorphismus. Der Vektorraum ${\displaystyle L(V,W)}$ hat also die Dimension ${\displaystyle m\cdot n}$.

Betrachtet man die Menge der linearen Selbstabbildungen eines Vektorraums, also den Spezialfall ${\displaystyle V=W}$, so bilden diese nicht nur einen Vektorraum, sondern mit der Verkettung von Abbildungen als Multiplikation eine assoziative Algebra, die kurz mit ${\displaystyle L(V)}$ bezeichnet wird.

Verallgemeinerung

Eine lineare Abbildung i​st ein Spezialfall e​iner affinen Abbildung.

Ersetzt m​an in d​er Definition d​er linearen Abbildung zwischen Vektorräumen d​en Körper d​urch einen Ring, erhält m​an einen Modulhomomorphismus.

Anmerkungen und Einzelnachweise

1. Diese Menge der linearen Abbildungen wird manchmal auch als ${\displaystyle {\text{Hom}}_{K}(V,W)}$ geschrieben.

Literatur

• Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 6., durchgesehene und ergänzte Auflage. Vieweg Braunschweig u. a. 2003, ISBN 3-528-56508-X, S. 124–143.
• Günter Gramlich: Lineare Algebra. Eine Einführung für Ingenieure. Fachbuchverlag Leipzig im Carl-Hanser-Verlag, München 2003, ISBN 3-446-22122-0.
• Detlef Wille: Repetitorium der Linearen Algebra. Band 1. 4. Auflage, Nachdruck. Binomi, Springe 2003, ISBN 3-923923-40-6.

Weblinks