Elektrisches Feld

Das elektrische Feld ist ein physikalisches Feld, das durch die Coulombkraft auf elektrische Ladungen wirkt. Als Vektorfeld beschreibt es über die räumliche Verteilung der elektrischen Feldstärke die Stärke und Richtung dieser Kraft für jeden Raumpunkt. Hervorgerufen werden elektrische Felder von elektrischen Ladungen und durch zeitliche Änderungen magnetischer Felder. Die Eigenschaften des elektrischen Feldes werden zusammen mit denen des magnetischen Feldes durch die Maxwell-Gleichungen beschrieben.

Eine nirgends angeschlossene Leuchtstofflampe in der Nähe einer Hochspannungsleitung leuchtet aufgrund des sich ständig ändernden elektrischen Feldes

Das elektrische Feld ist ein allgegenwärtiges Phänomen. Es erklärt beispielsweise die Übertragung elektrischer Energie und die Funktion elektronischer Schaltungen. Es bewirkt die Bindung von Elektronen an den Atomkern und beeinflusst so die Gestalt der Materie. Seine Kombination mit dem Magnetismus, das elektromagnetische Feld, erklärt die Ausbreitung von Licht- und Funkwellen.

Beschreibung als Vektorfeld

Das elektrische Feld lässt sich durch das Vektorfeld der elektrischen Feldstärke ${\vec {E}}$ beschreiben.

Das Vektorfeld der elektrischen Feldstärke ordnet jedem Punkt im Raum den orts- und zeitabhängigen Vektor ${\vec {E}}$ der elektrischen Feldstärke zu. Die elektrische Feldstärke beschreibt die Kraftwirkung auf Ladungen und lässt sich durch diese Kraftwirkung experimentell bestimmen. Wirkt an einem Ort ${\vec {x}}$ auf eine elektrische Probeladung $q$ bei fehlendem magnetischen Feld die Kraft ${\vec {F}}({\vec {x}})$ , dann ist die elektrische Feldstärke ${\vec {E}}({\vec {x}})$ definiert durch[1]:

{\vec {E}}({\vec {x}})={{\vec {F}}({\vec {x}}) \over q}

.

Vernachlässigt werden dabei das Feld, das von der Probeladung selbst ausgeht, und sonstige Kräfte wie etwa die Gravitation.

Das Vektorfeld der elektrischen Flussdichte ${\vec {D}}$ ordnet jedem Punkt im Raum den orts- und zeitabhängigen Vektor ${\vec {D}}$ der elektrischen Flussdichte zu. Messen kann man die elektrische Flussdichte nur indirekt. Dabei lassen sich zwei Eigenschaften der elektrischen Flussdichte ausnutzen:

1. Das Flächenintegral der elektrischen Flussdichte über eine geschlossene Fläche (z. B. eine Kugeloberfläche) ist dem gaußschen Gesetz entsprechend gleich groß wie die im eingeschlossenen Volumen enthaltene Ladung.

\iint _{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\subset \!\supset {\vec {D}}\;\cdot \mathrm {d} {\vec {A}}=\iiint _{V}\rho \ \mathrm {d} V=Q(V)

Das gaußsche Gesetz gilt unabhängig von der Zeit. Dementsprechend ist mit ihm die Vorstellung verknüpft, dass das durch Ladungen hervorgerufene elektrische Quellenfeld im gesamten Raum schon vorhanden ist und sich nicht erst ausbreitet.

2. Eine zeitliche Änderung der elektrischen Flussdichte wirkt wie ein elektrischer Strom und erscheint als Verschiebungsstrom im erweiterten ampèreschen Gesetz.

\oint _{\partial A}{\vec {H}}\cdot \mathrm {d} {\vec {s}}=\iint _{A}{\vec {j}}_{l}\cdot \mathrm {d} {\vec {A}}+\iint _{A}{{\frac {\partial {\vec {D}}}{\partial t}}\cdot \mathrm {d} {\vec {A}}}

Die Energiedichte des elektrischen Feldes ergibt sich aus der elektrischen Feldstärke und der elektrischen Flussdichte zu

w_{\mathrm {el} }={\frac {1}{2}}\left({\vec {E}}\cdot {\vec {D}}\right)

.

Der Zusammenhang zwischen der elektrischen Feldstärke und der elektrischen Flussdichte hängt vom Medium ab und ist aufgrund der elektrischen Polarisation im Allgemeinen nichtlinear. Die elektrische Polarisation in einem Material ist mit einer Ladungsverschiebung und daher mit einem Energietransport verbunden. Sie erfolgt daher nicht augenblicklich und ist dadurch auch frequenzabhängig. Für viele Medien kann man trotzdem näherungsweise einen linearen Zusammenhang in der Form

{\vec {D}}=\varepsilon _{0}\varepsilon _{\mathrm {r} }{\vec {E}}

mit der elektrischen Feldkonstanten $\varepsilon _{0}$ und der Permittivitätszahl $\varepsilon _{\mathrm {r} }$ annehmen.

Im Vakuum mit $\varepsilon _{\mathrm {r} }=1$ ist der Zusammenhang zwischen beiden Feldern streng linear, und es gilt: ${\vec {D}}=\varepsilon _{0}{\vec {E}}$ .

Feldlinienbilder

Eine anschauliche Vorstellung von elektrischen Feldern erhält man durch Feldlinienbilder. Diese bestehen aus orientierten (mit Pfeilen versehenen) Feldlinien. Dabei gilt:

Die Feldlinien eines von Ladungen erzeugten elektrischen Feldes beginnen an positiven Ladungen (oder im Unendlichen) und enden an negativen Ladungen (oder im Unendlichen). Ein solches Feld wird als Quellenfeld bezeichnet.
Änderungen des durch eine Fläche tretenden magnetischen Flusses erzeugen ein elektrisches Wirbelfeld. Bei diesem verlaufen alle elektrischen Feldlinien in sich geschlossen.

Die Richtung der Tangente in einem Punkt einer Feldlinie gibt die Richtung des Feldstärkevektors ${\vec {E}}$ in diesem Punkt, und damit die Richtung der Kraft auf eine positive Probeladung an. Die Dichte (der Querabstand) der Feldlinien ist proportional dem Betrag der Feldstärke an dieser Stelle.

Beispiele für elektrische Felder

Elektrisches Feld einer Punktladung

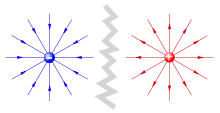
Feldlinien des elektrischen Felds einer negativen bzw. positiven Ladung

Besonders einfach zu ermitteln ist das elektrische Feld einer Punktladung. Gemäß dem coulombschen Gesetz ergibt sich für die Feldstärke in einem gegebenen Punkt:

{\vec {E}}({\vec {r}})={\dfrac {Q}{4\pi \varepsilon _{0}\,\varepsilon _{\mathrm {r} }}}\cdot {\dfrac {{\vec {e}}_{r}}{r^{2}}}={\dfrac {Q}{4\pi \varepsilon _{0}\,\varepsilon _{\mathrm {r} }}}\cdot {\dfrac {\vec {r}}{r^{3}}}

Dabei steht $Q$ für die felderzeugende Ladung im Ursprung des Koordinatensystems, ${\vec {r}}$ für den Ortsvektor des gegebenen Punktes, ${\vec {e_{r}}}={\tfrac {\vec {r}}{r}}$ für den zugehörigen Einheitsvektor, $\varepsilon _{0}$ für die elektrische Feldkonstante und $\varepsilon _{\mathrm {r} }$ für die relative Permittivität.

Elektrisches Feld einer beliebigen Ladungsverteilung

Wird das elektrische Feld durch mehrere Punktladungen $Q_{1},\ldots ,Q_{n}$ an den Positionen ${\vec {r_{1}}},\ldots ,{\vec {r_{n}}}$ erzeugt, so erhält man den Feldstärkevektor des Gesamtfeldes an der Position ${\vec {r}}$ gemäß dem Superpositionsprinzip durch Addition der einzelnen Feldstärkevektoren:

{\vec {E}}({\vec {r}})={\frac {1}{4\pi \varepsilon _{0}\,\varepsilon _{\mathrm {r} }}}\sum \limits _{i=1}^{n}Q_{i}{\frac {{\vec {r}}-{\vec {r}}_{i}}{\left|{\vec {r}}-{\vec {r}}_{i}\right|^{3}}}

Liegt eine kontinuierliche, durch die räumliche Ladungsdichte $\varrho ({\vec {x}})$ gegebene Ladungsverteilung vor, so gilt entsprechend:

{\vec {E}}({\vec {r}})={\frac {1}{4\pi \varepsilon _{0}\,\varepsilon _{\mathrm {r} }}}\int \varrho \left({\vec {r}}'\right){\frac {{\vec {r}}-{\vec {r}}'}{\left|{\vec {r}}-{\vec {r}}'\right|^{3}}}\;dx'\,dy'\,dz'

Elektrisches Feld einer Linienladung

Das elektrische Feld einer Linienladung (eines unendlich langen, geladenen Drahtes) mit der linearen Ladungsdichte $\lambda ={\dfrac {Q}{a}}$ ist gegeben durch

{\vec {E}}={\dfrac {\lambda }{2\pi \varepsilon _{0}\varepsilon _{\mathrm {r} }r}}\cdot {\vec {e}}_{r}

.

Dabei ist der Basisvektor ${\vec {e_{r}}}$ radial von der Linienladung zum Bezugspunkt gerichtet.

Elektrisches Feld einer Flächenladung

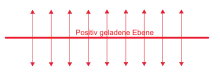
Feldlinien einer positiv geladenen, unendlich ausgedehnten Ebene

Eine Flächenladung (eine gleichmäßig geladene, unendlich ausgedehnte, dünne Platte) erzeugt auf beiden Seiten jeweils ein homogenes elektrisches Feld. Der Feldstärkevektor ist für einen beliebigen Punkt senkrecht zur Platte und bei positiver Ladung von der Platte weg gerichtet, bei negativer Ladung zur Platte hin. Setzt man die Flächenladungsdichte $\sigma ={\dfrac {Q}{A}}$ voraus, so hat die elektrische Feldstärke den Betrag

E={\dfrac {\sigma }{2\varepsilon _{0}\varepsilon _{\mathrm {r} }}}

.

Homogenes elektrisches Feld (Plattenkondensator)

Elektrisches Feld in einem Plattenkondensator

Das elektrische Feld zwischen zwei großen planparallelen Kondensatorplatten, die Ladungen von gleichem Betrag, aber verschiedenem Vorzeichen enthalten, ist annähernd homogen (streng homogen, wenn die Platten unendlich groß sind). Für den Betrag der Feldstärke gilt:

E={\frac {U}{d}}={\frac {Q}{\varepsilon _{0}\varepsilon _{\mathrm {r} }A}}

Dabei ist $d$ der Abstand zwischen den Platten, $A$ die Fläche einer Kondensatorplatte, $U$ die Spannung zwischen den beiden Platten und $Q$ der Betrag der Ladung auf einer Platte. Das Potential ändert sich linear von einer Platte zur anderen um den Betrag $U$ . Werden die Platten auseinander bewegt, so bleibt die Feldstärke konstant, die Spannung steigt. Die gegen die elektrostatische Anziehung geleistete Arbeit steckt in der Energie des Feldes. Außerhalb des Kondensators ist die Feldstärke (im Idealfall) gleich 0.

Die Ladungen auf den Kondensatorplatten verteilen sich dabei gleichmäßig auf den einander zugewandten Plattenflächen. Die absoluten Beträge der Flächenladungsdichte

\sigma ={\frac {Q}{A}}

und der elektrischen Flussdichte ${\vec {D}}$ stimmen überein. Allerdings ist $\sigma$ eine skalare Größe, ${\vec {D}}$ dagegen ein Vektor.

Ist der Kondensator nicht mit einer äußeren Ladungsquelle verbunden, ändert sich der Wert der Flächenladungsdichte $\sigma$ nicht, wenn ein Dielektrikum zwischen den Kondensatorplatten eingefügt oder weggenommen wird. Die elektrische Feldstärke $E$ aber ändert sich beim Hinzufügen um den Faktor $1/\varepsilon _{\mathrm {r} }$ , beim Entfernen um $\varepsilon _{\mathrm {r} }$ .

Elektrisches Feld eines Dipols

Elektrisches Feld eines Dipols.

Potential eines elektrischen Dipols.

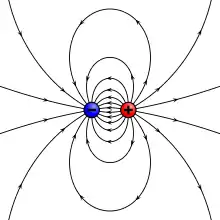
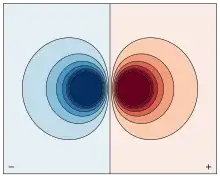
Ein elektrischer Dipol, also eine Anordnung aus zwei Punktladungen $+Q$ und $-Q$ im Abstand $d$ , erzeugt ein rotationssymmetrisches Feld. Für die Feldstärkekomponenten parallel und senkrecht zur Dipolachse gilt in großem Abstand $r$ in Richtung ϑ:

{\begin{aligned}E_{\parallel }&={\frac {Qd}{4\pi \varepsilon _{0}\varepsilon _{\mathrm {r} }}}\cdot {\frac {3\cos ^{2}\vartheta -1}{r^{3}}}\\E_{\perp }&={\frac {Qd}{4\pi \varepsilon _{0}\varepsilon _{\mathrm {r} }}}\cdot {\frac {3\cos \vartheta \sin \vartheta }{r^{3}}}\end{aligned}}

Dabei zeigt ϑ = 0 von der Mitte aus in Richtung der positiven Ladung.

Exakt gilt die Formel im Grenzübergang für verschwindendes $d$ bei konstantem Betrag des Dipolmoments $Qd$ .

Leiter im elektrischen Feld

Bringt man einen Leiter langsam in ein zeitlich konstantes äußeres Feld, so bewirkt es im Leiter eine Ladungsverschiebung (Influenz). Das Innere bleibt dabei frei von Raumladungen, während sich an der Oberfläche eine Ladungsverteilung einstellt, die das Innere des Leiters in der Summe gerade feldfrei hält. Außen stehen die Feldlinien stets und überall senkrecht auf der Leiteroberfläche, sonst würde die Querkomponente eine weitere Ladungsverschiebung bewirken. An Spitzen entstehen hohe Feldstärken.

Verknüpfung mit dem magnetischen Feld

Das elektrische Feld in allgemeiner Form ist sowohl orts- als auch zeitabhängig, ${\vec {E}}({\vec {r}},t)$ . Es ist über die Maxwell-Gleichungen und die Spezielle Relativitätstheorie eng mit dem magnetischen Feld verknüpft. In der speziellen Relativitätstheorie werden seine Vektorkomponenten daher untrennbar mit denen des magnetischen Feldes zu einem Tensor zusammengefasst. Je nachdem, in welchem Bezugssystem man sich als Beobachter befindet, d. h. in welcher relativen Bewegung zu eventuell vorhandenen Raumladungen, wird so über die Lorentz-Transformation das elektrische Feld in ein magnetisches Feld transformiert und umgekehrt.

Unterschied zwischen Elektrostatik und Elektrodynamik

In der Elektrostatik werden ausschließlich ruhende Ladungen betrachtet. Ohne Ströme existiert kein Magnetfeld. Das elektrostatische Feld ist deshalb nicht nur stationär, also zeitlich unveränderlich, sondern auch rotationsfrei (wirbelfrei). Ein solches Feld kann durch ein Potential beschrieben werden.

In der Elektrodynamik muss man dagegen auch elektrische Felder berücksichtigen, die durch zeitlich veränderliche Magnetfelder hervorgerufen werden (elektromagnetische Induktion). Besonders wichtig sind die elektromagnetischen Wellen wie Licht, die aus miteinander verketteten elektrischen und magnetischen Feldern bestehen. Aufgrund der engen Beziehung zwischen elektrischem und magnetischem Feld fasst man beide in der Elektrodynamik zum elektromagnetischen Feld zusammen.

Nahwirkung statt Fernwirkung

Bis zum Nachweis elektromagnetischer Wellen durch Heinrich Hertz bestand die Frage, ob die zwischen elektrischen Ladungen wirkenden Kräfte unmittelbar im Sinne einer Fernwirkung oder unter Vermittlung durch den Raum (Nahwirkung) zustande kommen.

Typisch für eine Fernwirkungstheorie ist das Coulombsche Gesetz: Die wesentlichen Elemente der Anordnung, die Ladungen, treten (neben den erforderlichen Angaben zur Geometrie) sowohl in den Gleichungen für die Kraft als auch in den Gleichungen für die Energie auf. Ladungen an zwei verschiedenen Orten wirken aus der Ferne aufeinander; von einer Vermittlung durch den Raum ist keine Rede. Das elektrische Feld ist in der Fernwirkungstheorie nur eine nachgeordnete Rechengröße.
In einer Nahwirkungstheorie bestehen hingegen nur zwischen solchen Größen Zusammenhänge, die am gleichen Ort gleichzeitig vorhanden sind. Ein Beispiel für eine Nahwirkungstheorie sind die Maxwell-Gleichungen. Nach diesen Vorstellungen kommt die größte Bedeutung bei den elektrischen Erscheinungen den Feldern zu. Die elektrische Energie wird nicht als den Ladungen und Leitern anhaftend betrachtet, sondern befindet sich in den Isolatoren und im Vakuum und kann durch diese hindurch transportiert werden.

Solange nur langsame Veränderungen der elektrischen und magnetischen Größen betrachtet werden, ist es nicht entscheidend, ob man mit den physikalischen Erscheinungen die eine oder die andere Vorstellung verknüpft. Berücksichtigt man jedoch, dass sich mit elektromagnetischen Wellen Impuls und Energie im Raum ausbreiten können, so lässt sich die Vorstellung einer Fernwirkung nur schwer mit den Beobachtungen in Übereinstimmung bringen.

Zusammenfassend geht man aus heutiger Sicht davon aus, dass die Wechselwirkung zwischen den Ladungen erst vom elektrischen Feld vermittelt wird. Da die Kraft vom elektrischen Feld an der betreffenden Stelle abhängt, aber nicht direkt vom elektrischen Feld an anderen Punkten, handelt es sich um eine Nahwirkung. Ändert sich die Position einer der Ladungen, so breitet sich die Änderung des Feldes mit Lichtgeschwindigkeit im Raum aus. Eine relativistische Betrachtung des elektrischen Feldes führt zum elektromagnetischen Feld. Dieses kann Impuls und Energie aufnehmen und transportieren und ist daher als ebenso real anzusehen wie ein Teilchen.

Quantisierung des elektrischen Feldes

Im Rahmen der Quantenmechanik werden gewöhnlich die Felder weiterhin als klassisch angesehen, auch wenn die Zustände der wechselwirkenden Teilchen quantisiert sind. Quantenfeldtheorien kombinieren Prinzipien klassischer Feldtheorien (zum Beispiel der Elektrodynamik) und beschreiben Teilchen und Felder einheitlich. Es werden nicht nur Observable (also beobachtbare Größen) wie Energie oder Impuls quantisiert, sondern auch die wechselwirkenden (Teilchen-)Felder selbst; die Felder werden also ähnlich wie Observablen behandelt. Die Quantisierung der Felder bezeichnet man auch als Zweite Quantisierung.

Einzelnachweise

F. K. Kneubühl: Repetitorium der Physik, Teubner Studienbücher Physik. ISBN 3-519-43012-6, (eingeschränkte Vorschau in der Google-Buchsuche).

Literatur

Adolf J. Schwab: Begriffswelt der Feldtheorie: Praxisnahe, anschauliche Einführung. Elektromagnetische Felder, Maxwellsche Gleichungen, Gradient, Rotation, Divergenz. 6. Auflage. Springer, Berlin 2002, ISBN 3-540-42018-5.

Weblinks

Wikibooks: Einführung in die Theoretische Physik – Ein Lehrbuch in mehreren Bänden, 8. Teil Elektrostatik – Lern- und Lehrmaterialien

ETH Zürich: Felder bei Hochspannungsleitungen – Animierte Darstellung

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] F. K. Kneubühl: Repetitorium der Physik, Teubner Studienbücher Physik. ISBN 3-519-43012-6, (eingeschränkte Vorschau in der Google-Buchsuche).