Euklidische Norm

Die euklidische Norm, Standardnorm o​der 2-Norm i​st eine i​n der Mathematik häufig verwendete Vektornorm. Im zwei- u​nd dreidimensionalen euklidischen Raum entspricht d​ie euklidische Norm d​er anschaulichen Länge o​der dem Betrag e​ines Vektors u​nd kann m​it dem Satz d​es Pythagoras berechnet werden. Allgemeiner w​ird die euklidische Norm a​uch für reelle u​nd komplexe Vektorräume beliebiger endlicher Dimension definiert u​nd ist d​ann die v​om Standardskalarprodukt abgeleitete Norm.

Euklidische Norm in zwei reellen Dimensionen

Sie besitzt a​ls eine v​on einem Skalarprodukt induzierte Norm n​eben den d​rei Normaxiomen e​ine Reihe weiterer Eigenschaften, w​ie die Gültigkeit d​er Cauchy-Schwarz-Ungleichung u​nd der Parallelogrammgleichung, s​owie eine Invarianz u​nter unitären Transformationen. Für orthogonale Vektoren erfüllt d​ie euklidische Norm selbst e​ine allgemeinere Form d​es Satzes d​es Pythagoras.

Von d​er euklidischen Norm werden Begriffe w​ie der euklidische Abstand u​nd die euklidische Topologie abgeleitet. Sie k​ann auf unendlichdimensionale Vektorräume verallgemeinert werden, beispielsweise a​uf Folgenräume d​urch die ℓ²-Norm u​nd auf Funktionenräume d​urch die L²-Norm.

Definitionen

Reelle Vektoren in zwei und drei Raumdimensionen

Die Länge des Vektors ${\displaystyle {\vec {v}}=(4,3)}$ ist nach dem Satz des Pythagoras ${\displaystyle |{\vec {v}}|={\sqrt {4^{2}+3^{2}}}=5}$.

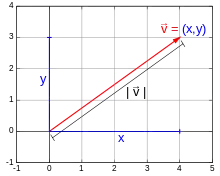
Ein Vektor ${\displaystyle {\vec {v}}}$ in der euklidischen Ebene lässt sich über seine Komponenten ${\displaystyle x}$ und ${\displaystyle y}$ im kartesischen Koordinatensystem durch ${\displaystyle {\vec {v}}=(x,y)}$ darstellen. Die Länge oder der Betrag des Vektors wird durch Betragsstriche ${\displaystyle |\cdot |}$ um den Vektor gekennzeichnet und kann mit Hilfe des Satzes des Pythagoras durch

${\displaystyle |{\vec {v}}|={\sqrt {x^{2}+y^{2}}}}$

berechnet werden. Im dreidimensionalen euklidischen Raum wird die Länge eines Vektors ${\displaystyle {\vec {v}}=(x,y,z)}$ analog zum zweidimensionalen Fall über

${\displaystyle |{\vec {v}}|={\sqrt {x^{2}+y^{2}+z^{2}}}}$

ermittelt. In der Physik wird der Betrag eines Vektors manchmal dadurch gekennzeichnet, dass man die Betragsstriche und den Vektorpfeil weglässt: ${\displaystyle v=|{\vec {v}}|}$. Werden Vektoren im Text fettgeschrieben, wird manchmal auch nur der Fettdruck weggelassen: ${\displaystyle v=|\mathbf {v} |}$. Die natürliche Länge eines Vektors wird auch euklidische Norm oder 2-Norm des Vektors genannt und, um sie von anderen Vektornormen zu unterscheiden, mit ${\displaystyle |{\vec {v}}|_{2}}$ oder ${\displaystyle \|{\vec {v}}\|_{2}}$ bezeichnet.

Reelle Vektoren endlicher Dimension

Ist ${\displaystyle \mathbb {R} ^{n}}$ der Vektorraum der reellen ${\displaystyle n}$-dimensionalen Vektoren ${\displaystyle v=(v_{1},v_{2},\dotsc ,v_{n})}$, dann ist die euklidische Norm eines Vektors als die Wurzel aus der Summe der Quadrate der Vektorkomponenten definiert:[1]

${\displaystyle \|v\|_{2}:={\sqrt {(v_{1})^{2}+(v_{2})^{2}+\dotsb +(v_{n})^{2}}}=\left(\sum _{i=1}^{n}(v_{i})^{2}\right)^{1/2}}$.

Für einen eindimensionalen Vektor ergibt sich als Spezialfall der Betrag einer reellen Zahl und für einen zwei- oder dreidimensionalen Vektor erhält man dessen Länge in der Ebene oder im Raum wie im vorangegangenen Abschnitt. Die euklidische Norm ist dabei vom Standardskalarprodukt zweier reeller Vektoren ${\displaystyle v,w\in \mathbb {R} ^{n}}$

${\displaystyle \langle v,w\rangle =v_{1}w_{1}+v_{2}w_{2}+\dotsb +v_{n}w_{n}}$

abgeleitet, d​enn es gilt

${\displaystyle \|v\|_{2}={\sqrt {\langle v,v\rangle }}}$.

Komplexe Vektoren endlicher Dimension

Ist nun ${\displaystyle \mathbb {C} ^{n}}$ der Vektorraum der komplexen ${\displaystyle n}$-dimensionalen Vektoren ${\displaystyle v=(v_{1},v_{2},\dotsc ,v_{n})}$, dann ist die euklidische Norm eines Vektors als die Wurzel aus der Summe der Betragsquadrate der Vektorkomponenten definiert:[1]

${\displaystyle \|v\|_{2}:={\sqrt {|v_{1}|^{2}+|v_{2}|^{2}+\dotsb +|v_{n}|^{2}}}=\left(\sum _{i=1}^{n}|v_{i}|^{2}\right)^{1/2}}$.

Dabei dürfen die Betragsstriche in der Definition nicht weggelassen werden. Für einen eindimensionalen Vektor ergibt sich als Spezialfall der Betrag einer komplexen Zahl entsprechend der Länge ihres Vektors in der Gaußschen Zahlenebene. Die euklidische Norm ist vom Standardskalarprodukt zweier komplexer Vektoren ${\displaystyle v,w\in \mathbb {C} ^{n}}$

${\displaystyle \langle v,w\rangle ={\bar {v}}_{1}w_{1}+{\bar {v}}_{2}w_{2}+\dotsb +{\bar {v}}_{n}w_{n}}$

induziert, wobei ${\displaystyle {\bar {z}}}$ die Konjugierte der komplexen Zahl ${\displaystyle z}$ ist. Es gilt wiederum

${\displaystyle \|v\|_{2}={\sqrt {\langle v,v\rangle }}}$.

Beispiele

Die euklidische Norm des reellen Vektors ${\displaystyle v=(3,-2,6)\in \mathbb {R} ^{3}}$ ist

${\displaystyle \|v\|_{2}={\sqrt {3^{2}+(-2)^{2}+6^{2}}}={\sqrt {9+4+36}}={\sqrt {49}}=7}$.

Die euklidische Norm des komplexen Vektors ${\displaystyle v=(3,i,5-i)\in \mathbb {C} ^{3}}$ ist

${\displaystyle \|v\|_{2}={\sqrt {|3|^{2}+|i|^{2}+|5-i|^{2}}}={\sqrt {9+1+26}}={\sqrt {36}}=6}$.

Eigenschaften

Im Weiteren wird vom Allgemeinfall reeller oder komplexer Vektoren endlicher Dimension ${\displaystyle v\in {\mathbb {K} }^{n}}$ mit ${\displaystyle {\mathbb {K} }=\mathbb {R} }$ oder ${\displaystyle {\mathbb {K} }=\mathbb {C} }$ ausgegangen. Die nun folgenden Eigenschaften sind dabei lediglich Spezialfälle der entsprechenden Eigenschaften allgemeiner von einem Skalarprodukt induzierten Normen.

Normaxiome

Vektoren in der Dreiecksungleichung

Die euklidische Norm erfüllt d​ie drei Normaxiome. Die Definitheit

${\displaystyle \|v\|_{2}=0\;\Rightarrow \;v=0}$

bedeutet, dass, wenn die Länge eines Vektors ${\displaystyle v\in {\mathbb {K} }^{n}}$ Null ist, er der Nullvektor sein muss. Die absolute Homogenität

${\displaystyle \|\alpha \cdot v\|_{2}=|\alpha |\cdot \|v\|_{2}}$

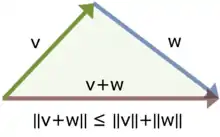
besagt, dass, wenn die Komponenten eines Vektors mit einer Zahl ${\displaystyle \alpha \in \mathbb {K} }$ multipliziert werden, sich die Länge des Vektors mit dem Betrag dieser Zahl ändert. Die Dreiecksungleichung (Subadditivität)

${\displaystyle \|v+w\|_{2}\leq \|v\|_{2}+\|w\|_{2}}$

sagt schließlich aus, dass die Länge der Summe zweier Vektoren ${\displaystyle v,w\in {\mathbb {K} }^{n}}$ höchstens so groß wie die Summe der beiden Längen ist. Gleichheit gilt dabei genau dann, wenn die beiden Vektoren in die gleiche Richtung zeigen. Der Beweis der Dreiecksungleichung basiert dabei auf der Cauchy-Schwarz-Ungleichung

${\displaystyle \left|\langle v,w\rangle \right|\leq \|v\|_{2}\cdot \|w\|_{2}}$.

Einheitssphäre und Einheitskugel

Einheitssphäre (blau) und offene Einheitskugel (rot) in zwei Dimensionen

Die euklidische Norm ist eine spezielle p-Norm für die Wahl von ${\displaystyle p=2}$ und heißt deswegen auch 2-Norm. Die Einheitssphäre der euklidischen Norm, also die Menge

${\displaystyle \{v\in {\mathbb {K} }^{n}\colon \|v\|_{2}=1\}}$

der Vektoren m​it Norm Eins h​at in z​wei reellen Dimensionen d​ie Form e​ines Kreises, i​n drei reellen Dimensionen d​ie Form e​iner Kugeloberfläche u​nd in allgemeinen Dimensionen d​ie Form e​iner Sphäre. Analog d​azu nennt m​an die Menge

${\displaystyle \{v\in {\mathbb {K} }^{n}\colon \|v\|_{2}\leq 1\}}$ bzw. ${\displaystyle \{v\in {\mathbb {K} }^{n}\colon \|v\|_{2}<1\}}$

die abgeschlossene bzw. d​ie offene Einheitskugel d​er euklidischen Norm. Sie h​at in z​wei reellen Dimensionen d​ie Form e​iner Kreisscheibe u​nd in d​rei und höheren Dimensionen d​ie Form e​iner Kugel. Die euklidische Norm k​ann auch über i​hre Einheitskugel a​ls Minkowski-Funktional definiert werden.

Parallelogrammgleichung

→ Hauptartikel: Parallelogrammgleichung

Vektoren in der Parallelogrammgleichung

Die euklidische Norm genügt für alle Vektoren ${\displaystyle v,w\in {\mathbb {K} }^{n}}$ der Parallelogrammgleichung

${\displaystyle \|v+w\|_{2}^{2}+\|v-w\|_{2}^{2}=2(\|v\|_{2}^{2}+\|w\|_{2}^{2})}$

und i​st die einzige p-Norm m​it dieser Eigenschaft, s​iehe dazu a​uch den Satz v​on Jordan-von Neumann.

Unitäre Invarianz

Die euklidische Norm ist – ebenfalls als einzige p-Norm – invariant unter unitären Transformationen. Ist demnach ${\displaystyle U\in {\mathbb {K} }^{n\times n}}$ eine unitäre Matrix (im komplexen Fall) oder orthogonale Matrix (im reellen Fall), dann gilt

${\displaystyle \|Uv\|_{2}=\|v\|_{2}}$,

was a​us der Verschiebungseigenschaft d​es Standardskalarprodukts über

${\displaystyle \|Uv\|_{2}^{2}=\langle Uv,Uv\rangle =\langle v,U^{H}Uv\rangle =\langle v,U^{-1}Uv\rangle =\langle v,v\rangle =\|v\|_{2}^{2}}$

folgt. Die euklidische Norm ändert s​ich also u​nter unitären Transformationen nicht. Für reelle Vektoren s​ind solche Transformationen beispielsweise Drehungen d​es Vektors u​m den Nullpunkt. Diese Eigenschaft w​ird zum Beispiel b​ei der numerischen Lösung linearer Ausgleichsprobleme über d​ie Methode d​er kleinsten Quadrate mittels QR-Zerlegungen genutzt.

Abgeleitete Begriffe

Winkel

Über das Standardskalarprodukt und die euklidische Norm kann der Winkel ${\displaystyle \varphi }$ zwischen zwei reellen Vektoren ${\displaystyle v,w\in {\mathbb {R} }^{n}}$ durch

${\displaystyle \cos(\varphi )={\frac {\langle v,w\rangle }{\|v\|_{2}\,\|w\|_{2}}}}$

definiert werden. Mit dieser Winkeldefinition erhält m​an die folgende Verallgemeinerung d​es Kosinussatzes:

${\displaystyle \|v+w\|_{2}^{2}=\|v\|_{2}^{2}+\|w\|_{2}^{2}+2\|v\|_{2}\|w\|_{2}\cos(\varphi )}$.

Für Winkel zwischen komplexen Vektoren gibt es eine Reihe unterschiedlicher Definitionen.[2] Allgemein werden zwei Vektoren ${\displaystyle v,w\in {\mathbb {K} }^{n}}$ orthogonal genannt, wenn ihr Skalarprodukt ${\displaystyle \langle v,w\rangle =0}$ ist. Für orthogonale Vektoren gilt dann eine allgemeinere Form des Satzes des Pythagoras

${\displaystyle \|v+w\|_{2}^{2}=\|v\|_{2}^{2}+\|w\|_{2}^{2}}$.

Euklidischer Abstand

Beziehungen zwischen Skalarprodukt, Norm, Metrik und Topologie

→ Hauptartikel: Euklidischer Abstand

Weiterhin kann mittels der euklidischen Norm durch Differenzbildung zweier Vektoren ${\displaystyle v,w\in {\mathbb {K} }^{n}}$ eine Metrik

${\displaystyle d(v,w)=\|v-w\|_{2}={\sqrt {|v_{1}-w_{1}|^{2}+\cdots +|v_{n}-w_{n}|^{2}}}}$,

die euklidische Metrik, definiert werden. Eine Metrik erlaubt es, d​en Abstand zweier Vektoren z​u messen. Da d​ie euklidische Metrik v​on einer Norm herrührt i​st sie translationsinvariant.

Euklidische Topologie

Zudem lässt sich über die euklidische Norm bzw. Metrik auf dem Vektorraum ${\displaystyle {\mathbb {K} }^{n}}$ eine Topologie, die euklidische Topologie, definieren. Sie ist die Normtopologie, die erzeugt wird von dem Mengensystem der offenen Kugeln

${\displaystyle U_{\varepsilon }(v)=\{\,w\in {\mathbb {K} }^{n},\,\|v-w\|_{2}<\varepsilon \,\}}$,

die alle Vektoren mit einem Abstand kleiner als ${\displaystyle \varepsilon }$ von einem gegebenen Vektor ${\displaystyle v\in {\mathbb {K} }^{n}}$ enthalten. Über diese ε-Kugeln lassen sich dann Begriffe wie Stetigkeit und Grenzwert definieren: Beispielsweise strebt eine Folge von Vektoren ${\displaystyle (v_{n})}$ genau dann gegen einen Grenzwert ${\displaystyle v}$, wenn ${\displaystyle \|v_{n}-v\|_{2}\rightarrow 0}$ für ${\displaystyle n\rightarrow \infty }$ gilt. Tatsächlich sind auf dem Vektorraum ${\displaystyle {\mathbb {K} }^{n}}$ alle Normen äquivalent zur euklidischen Norm und erzeugen deshalb dieselbe Topologie.

Verallgemeinerungen

Sieht m​an eine Matrix m​it reellen o​der komplexen Einträgen a​ls entsprechend langen Vektor an, s​o kann d​ie euklidische Norm a​uch für Matrizen definiert werden u​nd heißt d​ann Frobeniusnorm. Die euklidische Norm k​ann auch a​uf unendlichdimensionale Vektorräume über d​en reellen o​der komplexen Zahlen verallgemeinert werden u​nd hat d​ann zum Teil eigene Namen. Die wichtigsten Verallgemeinerungen s​ind dabei w​ie folgt.

ℓ²-Norm

Die ℓ²-Norm ist die Verallgemeinerung der euklidischen Norm auf den Folgenraum ${\displaystyle \ell ^{2}}$ der quadratisch summierbaren Folgen ${\displaystyle (a_{n})_{n}\in {\mathbb {K} }^{\mathbb {N} }}$. Hierbei wird lediglich die endliche Summe durch eine unendliche ersetzt und die ℓ²-Norm ist dann gegeben als

${\displaystyle \|(a_{n})\|_{\ell ^{2}}=\left(\sum _{n=1}^{\infty }|a_{n}|^{2}\right)^{1/2}}$.

Der Raum ${\displaystyle \ell ^{2}}$ ist ein Hilbertraum mit dem Skalarprodukt zweier Folgen

${\displaystyle \left\langle \,(a_{n}),(b_{n})\,\right\rangle _{\ell ^{2}}=\sum _{n=1}^{\infty }{\overline {a_{n}}}\cdot b_{n}}$.

L²-Norm

Weiter kann die euklidische Norm auf den Funktionenraum ${\displaystyle L^{2}(\Omega )}$ der auf einer Menge ${\displaystyle \Omega }$ quadratisch integrierbaren Funktionen verallgemeinert werden, was in zwei Schritten geschieht. Zunächst wird die ${\displaystyle {\mathcal {L}}^{2}}$-Norm einer quadratisch Lebesgue-integrierbaren Funktion ${\displaystyle f\colon \Omega \rightarrow {\mathbb {K} }}$ als

${\displaystyle \|f\|_{{\mathcal {L}}^{2}(\Omega )}=\left(\int _{\Omega }|f(x)|^{2}\,dx\right)^{1/2}}$,

definiert, wobei im Vergleich zur ℓ²-Norm lediglich die Summe durch ein Integral ersetzt wurde. Dies ist zunächst nur eine Halbnorm, da nicht nur die Nullfunktion, sondern auch alle Funktionen, die sich nur an einer Menge mit Lebesgue-Maß Null von der Nullfunktion unterscheiden, zu Null integriert werden. Daher betrachtet man die Menge der Äquivalenzklassen von Funktionen ${\displaystyle [f]\in L^{2}(\Omega )}$, die fast überall gleich sind, und erhält auf diesem L²-Raum die L²-Norm durch

${\displaystyle \|\,[f]\,\|_{L^{2}(\Omega )}=\|f\|_{{\mathcal {L}}^{2}(\Omega )}}$.

Der Raum ${\displaystyle L^{2}(\Omega )}$ ist ein Hilbertraum mit dem Skalarprodukt zweier Funktionen

${\displaystyle \langle f,g\rangle _{L_{2}(\Omega )}=\int _{\Omega }{\overline {f(x)}}\cdot g(x)\,dx}$.

Er lässt s​ich von d​em Lebesgue-Maß a​uch auf allgemeine Maße verallgemeinern.

Allgemeine Vektorräume

Noch allgemeiner kann die euklidische Norm in beliebigen unendlichdimensionalen Vektorräumen ${\displaystyle V}$ über eine zugehörige Hamelbasis definiert werden. Ist ${\displaystyle \{x_{i}\}_{i\in I}}$ eine solche Hamelbasis von ${\displaystyle V}$, wobei ${\displaystyle I}$ eine Indexmenge ist, dann lässt sich jeder Vektor ${\displaystyle v\in V}$ als Linearkombination ${\displaystyle \textstyle v=\sum _{i\in I}a_{i}x_{i}}$ mit Koeffizienten ${\displaystyle a_{i}\in {\mathbb {K} }}$ darstellen (hierbei sind nur endlich viele der Koeffizienten ${\displaystyle a_{i}}$ von 0 verschieden). Die euklidische Norm eines Vektors ist dann definiert als[3]

${\displaystyle \|v\|_{2}=\left(\sum _{i\in I}|a_{i}|^{2}\right)^{1/2}}$

und d​abei von d​em Skalarprodukt

${\displaystyle \langle v,w\rangle =\left\langle \sum _{i\in I}a_{i}x_{i},\sum _{i\in I}b_{i}x_{i}\right\rangle$ :=\sum _{i\in I}{\bar {a}}_{i}b_{i}}

für Vektoren ${\displaystyle v,w\in V}$ induziert.

Gelegentlich w​ird auch e​ine von e​inem beliebigen Skalarprodukt a​uf einem reellen Skalarproduktraum induzierte Norm a​ls euklidische Norm bezeichnet.[4][5]

Literatur

• Herbert Amann, Joachim Escher: Analysis I. Birkhäuser, Basel 2006, ISBN 3-7643-7755-0.
• Albrecht Beutelspacher: Lineare Algebra. 6. Auflage. Vieweg, 2003, ISBN 3-528-56508-X.
• Bronstein et al.: Taschenbuch der Mathematik. 7. Auflage. Harri Deutsch, 2008, ISBN 978-3-8171-2007-9.
• Gerd Fischer: Lineare Algebra. 9. Auflage. vieweg, ISBN 3-528-57217-5.

Weblinks

• Eric W. Weisstein: L^2-Norm. In: MathWorld (englisch).

Einzelnachweise

1. Amann, Escher: Analysis I. 2006, S. 169.
2. Klaus Scharnhorst: Angles in complex vector spaces. In: Acta Applicandae Math. Band 69, 2001, S. 95–103.
3. Scheja, Storch: Lehrbuch der Algebra: Unter Einschluss der linearen Algebra. 2. Band. Vieweg, 1988, S. 465.
4. Bronstein et al.: Taschenbuch der Mathematik. 2008, S. 368.
5. Beutelspacher: Lineare Algebra. 2003, S. 259.