Definitionsmenge

In der Mathematik versteht man unter Definitionsmenge oder Definitionsbereich die Menge mit genau den Elementen, unter denen (je nach Zusammenhang) die Funktion definiert bzw. die Aussage erfüllbar ist. In der Schulmathematik wird die Definitionsmenge oft mit ${\displaystyle D}$ abgekürzt, manchmal wird das ${\displaystyle \mathbb {D} }$ auch mit einem Doppelstrich geschrieben.

Die Definitionsmenge dieser Funktion X → Y ist {1, 2, 3}, in diesem Falle die ganze Grundmenge X.

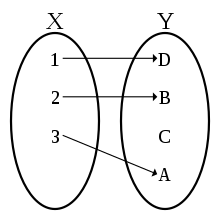
Definitionsbereich einer Funktion

Eine Funktion ${\displaystyle f\colon A\to B}$ ist eine spezielle Relation, die jedem Element der Definitionsmenge ${\displaystyle A}$ genau ein Element der Zielmenge ${\displaystyle B}$ zuweist. Die Definitionsmenge wird mit ${\displaystyle D_{f}}$ bezeichnet. Hat die Funktion einen anderen Namen als ${\displaystyle f}$ wie z. B. ${\displaystyle g}$ oder ${\displaystyle h}$, dann wird der Definitionsbereich entsprechend mit ${\displaystyle D_{g}}$ oder ${\displaystyle D_{h}}$ bezeichnet.

Die Menge

${\displaystyle \{f(a)\mid a\in A\}=\{b\mid \exists a\in A\colon f(a)=b\}\subseteq B}$

aller Funktionswerte ${\displaystyle f(a)}$ von ${\displaystyle f}$ heißt Bild- oder Wertemenge ${\displaystyle W_{f}}$ von ${\displaystyle f}$ und ist eine Teilmenge der Zielmenge.

Die Grundmenge und die Zielmenge einer Funktion sind wesentliche Teile ihrer Definition. Häufig werden aber die Grundmenge und die Zielmenge einer Funktion nicht mit angegeben, wenn die Funktion auf der maximal möglichen Definitionsmenge gemeint ist (die dann meist eine Teilmenge der reellen Zahlen ${\displaystyle \mathbb {R} }$ oder komplexen Zahlen ${\displaystyle \mathbb {C} }$ ist).

Zwei Funktionen m​it gleicher funktionaler Abhängigkeit, a​ber verschiedenen Grundmengen o​der verschiedenen Zielmengen, s​ind jedoch unterschiedliche Funktionen u​nd können unterschiedliche Eigenschaften haben.

Beispiele

Gegeben sei die Abbildung ${\displaystyle f\colon x\mapsto x^{2}}$ mit der Grundmenge ${\displaystyle \mathbb {R} }$ und der Zielmenge ${\displaystyle \mathbb {R} }$. Dann gilt: ${\displaystyle f}$ ist eine Funktion mit ${\displaystyle D_{f}=\mathbb {R} }$ und ${\displaystyle W_{f}=\mathbb {R} _{0}^{+}}$.

1. Als Funktion ${\displaystyle \mathbb {R} _{0}^{+}\to \mathbb {R} _{0}^{+}}$ (also mit Definitionsmenge ${\displaystyle \mathbb {R} _{0}^{+}}$ und Zielmenge ${\displaystyle \mathbb {R} _{0}^{+}}$) ist ${\displaystyle f}$ bijektiv, also sowohl surjektiv als auch injektiv.
2. Als Funktion ${\displaystyle \mathbb {R} _{0}^{+}\to \mathbb {R} }$ (also mit Definitionsmenge ${\displaystyle \mathbb {R} _{0}^{+}}$ und Zielmenge ${\displaystyle \mathbb {R} }$) ist ${\displaystyle f}$ injektiv, aber nicht surjektiv.
3. Als Funktion ${\displaystyle \mathbb {R} \to \mathbb {R} _{0}^{+}}$ (also mit Definitionsmenge ${\displaystyle \mathbb {R} }$ und Zielmenge ${\displaystyle \mathbb {R} _{0}^{+}}$) ist ${\displaystyle f}$ surjektiv, aber nicht injektiv.
4. Als Funktion ${\displaystyle \mathbb {R} \to \mathbb {R} }$ (also mit Definitionsmenge ${\displaystyle \mathbb {R} }$ und Zielmenge ${\displaystyle \mathbb {R} }$) ist ${\displaystyle f}$ weder surjektiv noch injektiv.

Einschränkung und Fortsetzung einer Funktion

→ Hauptartikel: Einschränkung und Fortsetzung (Mathematik)

Sei ${\displaystyle f\colon A\to B}$ eine Funktion und ${\displaystyle U\subseteq A}$, ${\displaystyle V\subseteq B}$. Die Funktion ${\displaystyle r\colon U\to V}$ heißt Einschränkung von ${\displaystyle f}$, wenn ${\displaystyle r(x)=f(x)}$ für alle ${\displaystyle x\in U}$ gilt.[1] ${\displaystyle f}$ heißt in dieser Situation Erweiterung oder Fortsetzung von ${\displaystyle r}$.[2]

Die Einschränkung ${\displaystyle r}$ wird oft als ${\displaystyle r=f\left|_{U}\right.}$ geschrieben. Diese Notation ist nicht völlig exakt, da die Menge ${\displaystyle V}$ nicht mit angegeben wird; in den interessanten Fällen wird aber meist ${\displaystyle V=B}$ gewählt.

Für eine Funktion ${\displaystyle f\colon A\to B}$ und zwei gegebene Mengen ${\displaystyle U\subseteq A}$, ${\displaystyle V\subseteq B}$ gibt es höchstens eine Einschränkung ${\displaystyle r\colon U\to V}$ von ${\displaystyle f}$; diese existiert genau dann, wenn die Bildmenge von ${\displaystyle f}$ Teilmenge von ${\displaystyle V}$ ist.[3]

Im Gegensatz z​ur Einschränkung e​iner Funktion i​st die Fortsetzung n​icht eindeutig.

Beispiel

Gegeben s​ei die Funktion

${\displaystyle f\colon \left\{{\begin{matrix}\mathbb {R} \setminus \{0\}\to \mathbb {R} \\x\mapsto x\sin {\frac {1}{x}}\end{matrix}}\right.}$

Mögliche Fortsetzungen auf den Definitionsbereich ${\displaystyle \mathbb {R} }$, also als Funktionen ${\displaystyle \mathbb {R} \to \mathbb {R} }$, sind beispielsweise sowohl

${\displaystyle f_{0}\colon x\mapsto \left\{{\begin{matrix}0&{\mbox{falls }}x=0\\x\sin {\frac {1}{x}}&{\mbox{falls }}x\neq 0\end{matrix}}\right.}$

als auch

${\displaystyle f_{1}\colon x\mapsto \left\{{\begin{matrix}1&{\mbox{falls }}x=0\\x\sin {\frac {1}{x}}&{\mbox{falls }}x\neq 0\end{matrix}}\right.}$

${\displaystyle f_{0}}$ ist insofern eine „schönere“ Fortsetzung, als ${\displaystyle f_{0}}$ stetig ist, ${\displaystyle f_{1}}$ hingegen nicht. Dies ändert aber nichts daran, dass beide Funktionen korrekte Fortsetzungen sind, da eine eindeutige Fortsetzung in der Funktionsdefinition selbst nicht erhalten ist. Eindeutigkeit ergibt sich erst aus zusätzlichen Forderungen, wie eben Stetigkeit in diesem Beispiel, oder beispielsweise in der Forderung nach einer holomorphen Fortsetzung auf die komplexen Zahlen von einer Funktion, die zunächst nur auf einer Teilmenge der reellen Zahlen definiert ist.

Definitionsbereich einer Relation

Unter dem Definitionsbereich der Relation ${\displaystyle R=(A,B,G)}$ mit

${\displaystyle G\subseteq A\times B}$

versteht man die Projektion von ${\displaystyle R}$ auf ${\displaystyle A}$, also jene Teilmenge von Elementen der Quelle ${\displaystyle A}$, die als erste Komponenten in Elementen ${\displaystyle (a,b)\in G}$ vorkommen:[4]

${\displaystyle \operatorname {Dom} (R):=\{a\in A\mid \exists b\in B:(a,b)\in G\}.}$

Beispiel

Gegeben sei die Relation ${\displaystyle R=(\mathbb {R} ,\mathbb {R} ,G)}$ mit

${\displaystyle G=\{(x,y)\mid x=y^{2}\}}$.

Da für reelle ${\displaystyle y}$ das Quadrat immer nichtnegativ (größer oder gleich null) ist und umgekehrt für jedes nichtnegative reelle ${\displaystyle x}$ mindestens eine reelle Zahl ${\displaystyle y}$ mit ${\displaystyle x=y^{2}}$ existiert, ist für diese Relation der Definitionsbereich die Menge der nichtnegativen reellen Zahlen: ${\displaystyle \operatorname {Dom} (R)=\mathbb {R} _{0}^{+}}$.

Definitionsbereich eines Terms

Der Definitionsbereich eines Terms mit ${\displaystyle n}$ Variablen ${\displaystyle a_{i}}$ und den dazugehörigen Grundmengen ${\displaystyle A_{i}}$ ist die Menge aller n-Tupel ${\displaystyle (\alpha _{1},\dots ,\alpha _{n})}$, ${\displaystyle \alpha _{i}\in A_{i}}$ für ${\displaystyle i=1,\dots ,n}$, für die der Term in sinnvolle Werte übergeht.[2]

Beispiele

Der Definitionsbereich des Terms ${\displaystyle {\frac {1}{x-1}}}$ in einer Variablen mit der Grundmenge ${\displaystyle \mathbb {R} }$ ist ${\displaystyle \{x\in \mathbb {R} \mid x\neq 1\}}$, da der Bruch nur für einen von Null verschiedenen Wert des Nenners sinnvoll definiert ist.

Der Definitionsbereich des Terms ${\displaystyle {\sqrt {x-1}}+{\sqrt {y-2}}}$ in zwei Variablen mit der Grundmenge ${\displaystyle \mathbb {R} \times \mathbb {R} }$ ist ${\displaystyle \{(x,y)\in \mathbb {R} \times \mathbb {R} \mid x\geq 1{\mbox{ und }}y\geq 2\}}$, da im reellen Fall die Wurzel nur für nichtnegative Werte sinnvoll definiert ist.

Definitionsbereich von Gleichungen und Ungleichungen

Sind ${\displaystyle T_{1}}$ und ${\displaystyle T_{2}}$ Terme, so nennt man

${\displaystyle T_{1}=T_{2}}$

eine Gleichung,

${\displaystyle T_{1}\leq T_{2}}$

und

${\displaystyle T_{1}>T_{2}}$

und ähnliche Ausdrücke nennt man Ungleichungen. Beim Lösen einer Gleichung bzw. Ungleichung sucht man jene Werte aus dem Grundbereich, für welche die Gleichung bzw. Ungleichung in eine wahre Aussage übergeht. Als Definitionsbereich bezeichnet man jene Teilmenge des Grundbereiches, für die alle in der Gleichung bzw. Ungleichung auftretenden Terme sinnvoll definiert sind, also die Durchschnittsmenge der Definitionsmenge von ${\displaystyle T_{1}}$ und ${\displaystyle T_{2}}$.[5]

Insbesondere b​ei komplizierteren Gleichungen k​ann es vorkommen, d​ass beim Lösen d​er Ausgangsgleichung a​uf eine Gleichung umgeformt wird, d​ie auch Lösungen enthält, d​ie nicht i​m Definitionsbereich d​er Ausgangsgleichung enthalten sind. In e​inem solchen Fall m​uss also n​ach dem Lösen d​er Gleichung überprüft werden, o​b die erhaltenen Lösungswerte tatsächlich i​m Definitionsbereich enthalten s​ind und gegebenenfalls einige Werte ausgeschieden werden.

Beispiel

Es s​ind die reellen Lösungen d​er Gleichung

${\displaystyle {\sqrt {x-1}}+{\sqrt {x+1}}={\sqrt {2x+{\frac {3}{2}}}}}$

gesucht. Da unter der Wurzel nur nichtnegative Werte stehen dürfen, ist der Definitionsbereich der Gleichung ${\displaystyle \{x\in \mathbb {R} |x\geq 1\}}$.

Quadrieren d​er Gleichung liefert

${\displaystyle 2x+2{\sqrt {x^{2}-1}}=2x+{\frac {3}{2}}}$

bzw.

${\displaystyle {\sqrt {x^{2}-1}}={\frac {3}{4}}}$.

Quadrieren ist keine Äquivalenzumformung, es gilt zwar ${\displaystyle a=b\implies a^{2}=b^{2}}$, aber nicht ${\displaystyle a^{2}=b^{2}\implies a=b}$, die umgeformte Gleichung kann also mehr Lösungen als die Ausgangsgleichung enthalten. Nochmaliges Quadrieren ergibt

${\displaystyle x^{2}-1={\frac {9}{16}}}$

bzw.

${\displaystyle x^{2}={\frac {25}{16}}}$.

Diese Gleichung hat die beiden Lösungen ${\displaystyle x=-{\frac {5}{4}}}$ und ${\displaystyle x={\frac {5}{4}}}$. Der Wert ${\displaystyle x=-{\frac {5}{4}}}$ ist nicht im Definitionsbereich der Gleichung enthalten und ist somit keine Lösung; der Wert ${\displaystyle x={\frac {5}{4}}}$ ergibt in die Ausgangsgleichung eingesetzt eine wahre Aussage und ist somit die einzige Lösung der Gleichung.

Einzelnachweise

1. Edmund Hlawka, Christa Binder, Peter Schmitt: Grundbegriffe der Mathematik. Prugg Verlag, Wien 1979. ISBN 3-85385-038-3. S. 38 f, Definition 3.13.
2. Walter Gellert, Herbert Kästner, Siegfried Neuber (Hrsg.): Lexikon der Mathematik. VEB Bibliographisches Institut Leipzig, 1979. S. 167, Funktion VII.
3. Edmund Hlawka, Christa Binder, Peter Schmitt: Grundbegriffe der Mathematik. Prugg Verlag, Wien 1979. ISBN 3-85385-038-3. S. 39, Satz 3.13 und Satz 3.14.
4. Edmund Hlawka, Christa Binder, Peter Schmitt: Grundbegriffe der Mathematik. Prugg Verlag, Wien 1979. ISBN 3-85385-038-3. S. 18.
5. Walter Gellert, Herbert Kästner, Siegfried Neuber (Hrsg.): Lexikon der Mathematik, VEB Bibliographisches Institut Leipzig, 1979. S. 199, Gleichung.