Computergrafik
Die Computergrafik ist ein Teilgebiet der Informatik, das sich mit der computergestützten Bilderzeugung,[1] im weiten Sinne auch mit der Bildbearbeitung[2] befasst. Mit den Mitteln der Computergrafik entstandene Bilder werden Computergrafiken genannt.
Die Computergrafik umfasst zum einen die Erzeugung von Grafiken, deren Bestandteile sich zweidimensional in der Ebene beschreiben lassen. Weitere Teilbereiche beschäftigen sich mit der Frage, wie sich komplexe Formen geometrisch modellieren lassen und wie aus daraus aufgebauten virtuellen Umgebungen Bilder oder Animationen berechnet (gerendert) werden können.
Ihren Ursprung hat die Computergrafik in den 1950er-Jahren, als Rechner mit grafischen Ausgabegeräten ausgestattet wurden. In der Folge wurden Eingabegeräte entwickelt, die eine interaktive Bedienung von Computern ermöglichten und vor allem wissenschaftlichen und technischen Anwendungen wie CAD und CAM den Weg bereiteten. Heute sind Computergrafiken allgegenwärtig; ihre Anwendungen reichen von grafischen Benutzeroberflächen über Druckerzeugnisse, Computerspiele und Filmtechnik bis hin zur Medizin.
Geschichte

Als Beginn der Computergrafik gilt oft der Anfang der 1950er Jahre am MIT entwickelte Whirlwind[3], der als erster Rechner über einen Kathodenstrahlröhren-Bildschirm sowie über ein lichtgriffelähnliches Eingabegerät verfügte und direkt zum interaktiven Luftraumüberwachungssystem SAGE führte. Außerdem kamen die ersten kommerziellen Vektorbildschirme auf den Markt, die Punkte und Linien anzeigen konnten. Parallel dazu entwickelte General Motors ein erstes interaktives CAD-System, das DAC-1.
Besonderen Einfluss auf die Entwicklung der interaktiven Computergrafik hatte Ivan Sutherlands 1963 vorgestelltes Sketchpad-Zeichensystem,[3] das viele auch in moderner Grafiksoftware gebräuchliche Interaktionsmöglichkeiten aufzeigte. Da Anfang der 1960er Jahre noch überwiegend mit Lochkarten gearbeitet wurde, bestand zwar eine Nachfrage nach interaktiven Benutzerschnittstellen, doch waren entsprechende Systeme äußerst kostspielig. Dies änderte sich gegen Ende des Jahrzehnts, als erste Computerterminals mit Speicherröhren-Grafikbildschirmen (Direct-View Storage Tubes) auf dem Markt erschienen und zehntausenden Anwendern einen erschwinglichen Zugang zur Computergrafik ermöglichten.[4] Zu dieser Zeit wurden außerdem wichtige Verfahren der 3D-Computergrafik wie Raytracing und Scanline-Algorithmen entwickelt.

In den 1980er Jahren setzten sich weitere Eingabegeräte wie Maus und Grafiktablett durch; auch Farbdrucker kamen auf den Markt. Gleichzeitig wurden Vektorbildschirme allmählich von Rasterbildschirmen, die farbig gefüllte Flächen anzeigen konnten, verdrängt. 1974 hielt ACM SIGGRAPH, heute die größte Vereinigung von Forschern und Branchenvertretern im Bereich Computergrafik, ihre erste Konferenz ab. Der ab Ende der 1970er Jahre massenhaft produzierte Personal Computer verfügte zwar über vergleichsweise schlechte Grafikmöglichkeiten, trieb jedoch die Hersteller dazu an, preisgünstige Plotter und Grafiktabletts herzustellen und trug so zur Verbreitung der Computergrafik entscheidend bei.
Die Systemleistung von PCs und Workstations stieg in den 1980er Jahren derartig an, dass nun auch Endbenutzer mit einfach zu bedienenden Programmen Computergrafiken erzeugen konnten. Außerdem gelangten die wichtigen Anwendungsgebiete CAD und CAM zum Durchbruch. Sowohl für diese als auch für andere Anwendungen kam erste 3D-Grafiksoftware auf den Markt. Künstlerische Anwendungen hatten zwar schon immer die Computergrafik begleitet, erschlossen nun aber als Computer Generated Imagery für die Film- und Werbebranche einen Markt.
In den 1990er Jahren erreichten übliche Rechner ausreichend Leistung, um unterschiedliche Techniken, etwa Computergrafik und Bildverarbeitung oder Bild- und Toninhalte, kombinieren zu können. Unter dem Schlagwort Multimedia verschwammen die Grenzen zwischen reiner Computergrafik und anderen Gebieten. Im Laufe des Jahrzehnts verschob sich außerdem das Gewicht von wissenschaftlichen und technischen zunehmend auf nichttechnische Anwendungsgebiete.[5] Dies machte sich unter anderem darin bemerkbar, dass vollständig computergenerierte Kinofilme in Spielfilmlänge produziert wurden. Mitte der 1990er Jahre wurde auch im nichtprofessionellen Bereich Hardwarebeschleunigung für 3D-Computergrafik eingeführt.
Seit Beginn des 21. Jahrhunderts besteht sowohl in der Fotografie als auch in der Bildsynthese ein lebhaftes Interesse an Hochkontrastbildern (High Dynamic Range Images). Die Echtzeitgrafik profitiert von leistungsfähigen Grafikprozessoren, die mittels programmierbarer Shader vielfältige Effekte erzeugen können. Bestrebungen, die für eine realistische Wirkung oft unverzichtbare globale Beleuchtung in Echtzeit zu berechnen, gelangen bisher (2010) jedoch nur teilweise.
Zweidimensionale Grafik
Raster- und Vektorgrafiken
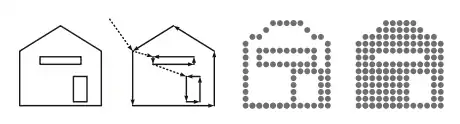
Seit den 1980er Jahren sind nur noch Rasterbildschirme üblich, bei denen das anzuzeigende Bild durch ein Raster aus Bildpunkten (Pixeln) repräsentiert wird, denen jeweils ein Farbwert zugeordnet ist. Bilder, die in dieser Form vorliegen, werden Rastergrafiken genannt. Sie können sowohl von Software erzeugt werden, als auch das Ergebnis einer Digitalisierung sein. Ein wichtiger Vorteil von Rasterbildschirmen ist die Fähigkeit, farbig gefüllte Flächen anzuzeigen. Auch viele Drucker und weitere Ausgabegeräte verwenden ein Punktraster. Allerdings leiden Rastergrafiken an Darstellungsproblemen wie dem Treppeneffekt, der ein Ergebnis der begrenzten Bildauflösung (Pixelanzahl) ist. Der sichtbare Teil des Framebuffers, ein besonderer Speicherbereich der Grafikkarte, enthält das auf dem Bildschirm angezeigte Bild in einem geräteabhängigen Datenformat.
Für die permanente Speicherung und den systemübergreifenden Austausch von Rastergrafiken wurden mehrere standardisierte Dateiformate entwickelt. Diese Grafikformate variieren erheblich in ihren Eigenschaften, etwa in der Unterstützung diverser Bildkompressionsverfahren. In Grafikdateien werden aus Speicherplatzgründen oft indizierte Farben verwendet, bei denen die im Bild verwendeten Farben in einer separaten Tabelle gespeichert sind. Rastergrafiken können außerdem einen Alphakanal enthalten, der die „Durchsichtigkeit“ jedes Pixels angibt.
Manche Arten von Bildern, etwa Strichzeichnungen oder Diagramme, werden besser als Vektorgrafiken gespeichert. Hierbei werden keine Pixel, sondern die grafischen Grundobjekte (Primitive), aus denen sich das Bild zusammensetzt, gespeichert. Diese Art der Repräsentation ist unabhängig von der Bildauflösung und erlaubt die verlustfreie Bearbeitung der Bildinhalte. Um eine Vektorgrafik auf Rasterbildschirmen anzeigen zu können, muss sie zunächst in eine Rastergrafik umgewandelt werden. Dieser Vorgang wird Rasterung genannt.
Rasteralgorithmen

Bei 2D-Vektorgrafiken sind verschiedene grafische Grundobjekte gebräuchlich. Hierzu zählen Linien, Kreise, Ellipsen, Polygone und andere Kurven. Alle diese Grundobjekte müssen erst gerastert werden, um sie auf einem Rasterbildschirm darstellen zu können. Dabei müssen auch Parameter wie Füll- und Linienfarben, Linienstärken und Linienstile berücksichtigt werden. Bei der Rasterung von Linien, Kreisen, Ellipsen und Polygonen werden oft iterative (schrittweise arbeitende) Algorithmen verwendet, die ausgehend vom Anfangspunkt entscheiden, welches Pixel jeweils als nächstes eingefärbt werden soll.
Oft muss die Rasterung einer Vektorgrafik auf einen bestimmten Bereich, zum Beispiel ein rechteckiges Fenster, begrenzt werden. Dies geschieht am einfachsten, indem die Grundobjekte vollständig gerastert, aber nur diejenigen Pixel eingefärbt werden, die sich tatsächlich innerhalb des gewünschten Bildausschnitts befinden. Es wurden jedoch verschiedene effizientere Methoden entwickelt, bei denen ein Grundobjekt vor der Rasterung auf den Bildausschnitt zugeschnitten wird. Derartige Clipping-Algorithmen kommen sowohl bei der 2D- als auch bei der 3D-Computergrafik zum Einsatz.
Zur Füllung beliebiger zusammenhängender Farbflächen werden Floodfill-Algorithmen angewandt. Bei der einfarbigen Rasterung kann es neben dem unausweichlichen Treppeneffekt zu weiteren Problemen wie etwa „fehlenden“ Pixeln kommen, die von der endlichen Auflösung des Ausgabegerätes herrühren. Besonders bei Schriftzeichen ist dies ein Problem. Hier muss sogenanntes Hinting angewandt werden, um die Zeichen auch bei kleiner Schriftgröße oder auf niedrig auflösenden Bildschirmen in bestmöglicher Qualität darstellen zu können.
Abtastung und Antialiasing

Beim Rastern eines Bildes muss jedem Pixel ein Farbwert zugeordnet werden, der die ideale Bildbeschreibung an diesem Punkt möglichst gut repräsentiert. Komplexere Bildbeschreibungen lassen sich nur an einzelnen Punkten auswerten, was im Sinne der Signalverarbeitung als Abtastung interpretiert werden kann. Hierbei können kleine Figuren durch das Pixelraster fallen oder Aliasing-Effekte auftreten, bei denen regelmäßig angeordnete, sehr kleine Bilddetails völlig falsch dargestellt werden. In der Computergrafik tritt dieses Problem besonders zutage, da das ideale Bild meist harte Objektkanten enthält.
Methoden, die die als Folge der Abtastung auftretenden unerwünschten Effekte abzuschwächen versuchen, werden Antialiasing genannt. Dazu werden die ein Pixel umgebenden Bildregionen in die Rasterung mit einbezogen. Selbst kleine Details fließen so in die Farbe eines Pixels ein, auch wenn sie zwischen zwei Pixeln liegen sollten. Der Treppeneffekt lässt sich durch Antialiasing ebenfalls deutlich reduzieren.
Helligkeit und Farbe
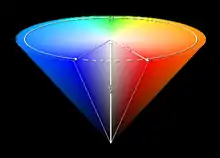
Der Farbwert jedes Pixels einer Rastergrafik wird üblicherweise mittels Rot-, Grün- und Blau- (RGB-)Werten angegeben. Die Anzahl der Werte, die jeder dieser drei Farbkanäle annehmen kann, wird durch die Farbtiefe angegeben; viele Bildschirme erlauben 256 Werte pro Farbkanal (True Color). Zur Auswahl von Farben durch den Anwender ist der RGB-Farbraum jedoch nicht der benutzerfreundlichste. In Zeichenprogrammen sind andere Farbräume wie der HSV-Farbraum gebräuchlich, bei dem eine Farbe durch Farbton, Sättigung und Helligkeit definiert wird. Beim Vierfarbendruck wird mit dem CMYK-Farbmodell gearbeitet.
Die Helligkeit der Bildschirmpixel ist nicht proportional zu den im Framebuffer angegebenen Farbwerten. Ein Graustufenwert von 50 % wird auf dem Bildschirm nicht als Grau mit 50 % Helligkeit dargestellt, sondern dunkler. Um korrekte Helligkeiten auszugeben, müssen daher computergenerierte Bilder stets eine Gammakorrektur oder – je nach Bildschirmtyp – andere Helligkeitsanpassungen durchlaufen. Damit eine möglichst konsistente Farbdarstellung auf verschiedenen Geräten gewährleistet ist, können zusätzlich Farbmanagement-Techniken angewandt werden.
Manchmal ist es nötig, die Anzahl der Farben einer Rastergrafik zu verringern. Dies geschieht mittels Farbreduktion, bei der die für die Grafik repräsentativsten Farben ausgewählt werden müssen. Zusätzlich kann Dithering angewandt werden, um den bei der Farbreduktion entstandenen Fehler zu streuen. Für die Ausgabe auf Druckern gibt es spezielle Methoden, um Druckraster zu erzeugen.
Einige Grafikformate erlauben es, die Farbwerte eines Bildes mit einem sehr hohen Helligkeitsumfang anzugeben. Derartige High Dynamic Range Images (HDRIs) speichern einen wesentlich naturgetreueren Bildeindruck als herkömmliche Formate und ermöglichen nachträgliche Helligkeitsänderungen ohne Qualitätsverlust. Allerdings sind aktuell (im Jahr 2010) nur wenige Bildschirme zur annähernden Wiedergabe von HDRIs in der Lage.
Geometrische Modellierung
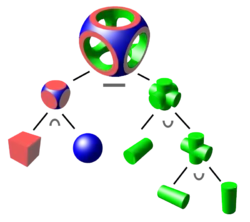
Die geometrische Modellierung ist die computergestützte Beschreibung sowohl von zweidimensionalen Kurven als auch von dreidimensionalen Flächen und Körpern. Neben ihrer Verwendung in der Computergrafik bildet sie die Basis von ingenieurtechnischen und wissenschaftlichen Anwendungen, zum Beispiel physikalischen Simulationen.
Körper können auf verschiedene Weise repräsentiert werden; jedes Darstellungsschema besitzt Vor- und Nachteile im Hinblick auf Speicheranforderungen, Präzision und Komplexität. Nicht jedes Schema garantiert, dass immer physikalisch realisierbare Körper repräsentiert werden. Man unterscheidet zwischen direkten Darstellungsschemata, bei denen das Volumen des Körpers selbst beschrieben wird, und indirekten Schemata, bei denen die Beschreibung eines Körpers über dessen Kanten und Oberflächen erfolgt. Diese beiden Methoden können auch kombiniert werden.
Die beiden am häufigsten verwendeten Darstellungsschemata sind Constructive Solid Geometry (CSG) und Oberflächendarstellungen.[6] CSG ist ein direktes Darstellungsschema, bei dem Objekte mit Hilfe von Grundkörpern wie Kugeln, Quadern oder Zylindern modelliert werden. Auf diese Grundkörper werden Operationen wie Vereinigung, Schnitt und Differenz angewandt, sodass sich am Ende eine Formel ergibt, die beschreibt, wie die Grundkörper miteinander verknüpft werden. CSG ist besonders im CAD-Bereich gebräuchlich, da sich damit viele dort verwendete Objekte auf natürliche Weise beschreiben lassen.

Bei der Oberflächendarstellung (Boundary Representation) hingegen wird ein Körper anhand seiner Oberfläche beschrieben; es handelt sich also um ein indirektes Darstellungsschema. Die mittels Oberflächendarstellung modellierten Objekte werden meist aus sogenannten Freiformflächen zusammengesetzt, die sich an Kontrollpunkten verformen lassen. Lokale Änderungen am Modell sind damit einfach möglich. Eine weitverbreitete Art von Freiformflächen sind Non-Uniform Rational B-Splines (NURBS). Vor der Darstellung werden NURBS aus Effizienzgründen üblicherweise in Polygon- oder Dreiecksnetze umgewandelt (trianguliert). Auch allgemeine zweidimensionale Kurven werden meist mittels Splines beschrieben, deren Kurvenverlauf durch Kontrollpunkte festgelegt wird. Hier sind Bézierkurven gebräuchlich, die für die Rasterung in Polygonzüge umgewandelt werden.
Das Ergebnis der 3D-Modellierung ist eine Szene, die neben der Objektgeometrie Materialeigenschaften, Lichtquellen sowie die Position und Blickrichtung eines virtuellen Betrachters enthält.
Dreidimensionale Grafik
Ausgehend von einer Szene werden durch Bildsynthese, auch Rendern genannt, 3D-Computergrafiken berechnet. Dieser Prozess läuft im Gegensatz zur Modellierung automatisch ab. Man unterscheidet zwischen der interaktiven Synthese von Bildern in Echtzeit, bei der meist Hardwarebeschleunigung zum Einsatz kommt, und der realistischen Bildsynthese, bei der vor allem auf hohe Bildqualität oder physikalische Korrektheit Wert gelegt wird.
Echtzeitrendern
Beim Echtzeitrendern wird eine Reihe von Bildern mit hoher Bildfrequenz berechnet und die zugrundeliegende Szene vom Anwender interaktiv verändert. Mit wenigen Ausnahmen unterstützt Grafikhardware als grafische Grundobjekte nur Punkte, Linien und Dreiecke,[7] andere Darstellungsschemata müssen daher erst in Dreiecksnetze umgewandelt werden.
Beim Echtzeitrendern beschreibt die Grafikpipeline modellhaft den Weg von der Szene bis zum fertigen Bild. Dieser Prozess wird von heutigen Grafikkarten größtenteils direkt in Hardware ausgeführt. Eine Ausnahme sind Techniken wie Kollisionserkennung, Animation oder Morphing, die die Szene verändern und für die das Anwendungsprogramm verantwortlich ist.
Viele Schritte der Grafikpipeline dienen dazu, die Grundobjekte der Szene schrittweise in anderen Koordinatensystemen auszudrücken, die die Berechnung vereinfachen. Dazu zählt meist eine Zentralprojektion, um eine perspektivische Abbildung zu erhalten. Außerdem kommen Clipping- und Culling-Techniken zum Einsatz, um außerhalb des sichtbaren Volumens liegende Flächen zu beschneiden oder zu entfernen. Nach Abschluss der verschiedenen Koordinatentransformationen befinden sich die projizierten Grundobjekte an der richtigen Bildschirmposition. Dort werden sie gerastert, indem die zu ihnen gehörenden Pixel eingefärbt werden. Da bei überlappenden Dreiecken nur die vom Betrachter aus sichtbaren Teile angezeigt werden sollen, wird mittels Z-Buffering eine Verdeckungsberechnung ausgeführt.
Zur Ansteuerung von Grafikpipelines werden üblicherweise Grafik-APIs verwendet, die die Grafikhardware abstrahieren und dem Programmierer viele Aufgaben abnehmen. Im professionellen Bereich hat der Standard OpenGL die größte Bedeutung, während unter Windows laufende Programme, insbesondere Computerspiele, vornehmlich DirectX nutzen.
Shading
Als Shading („Schattierung“) wird im Allgemeinen die Berechnung der Farben an Oberflächen anhand der zugehörigen Materialeigenschaften und dem direkt von den Lichtquellen eintreffenden Licht bezeichnet. Shading kommt sowohl beim Echtzeitrendern als auch beim realistischen Rendern zum Einsatz. Die indirekte Beleuchtung durch Lichtreflexion zwischen Objekten bleibt dabei zunächst unberücksichtigt. Einen Spezialfall stellt sogenanntes Non-photorealistic Rendering dar, bei dem zum Beispiel aus ästhetischen Gründen Verfremdungen erzeugt werden.

Zur Beschreibung des Reflexionsverhaltens einer Oberfläche werden lokale Beleuchtungsmodelle verwendet, mit denen sich diverse Materialien simulieren lassen. Das lambertsche Gesetz eignet sich beispielsweise für matte Flächen wie Wände, während mit dem Phong-Beleuchtungsmodell glänzende Oberflächen dargestellt werden können. Beim Echtzeitrendern werden häufig für die Eckpunkte eines Dreiecks die Farben berechnet und diese anschließend innerhalb des Dreiecks interpoliert (Gouraud Shading). Dadurch ergibt sich ein weniger kantiges Erscheinungsbild als beim Flat Shading, bei dem Dreiecke einheitlich mit einer Farbe gefüllt werden.
Um Oberflächendetails zu simulieren, werden Mapping-Techniken eingesetzt, die die Material- oder Geometrieeigenschaften an jedem Punkt der Oberfläche anhand einer Funktion oder Rastergrafik variieren. So etwa dient Texture Mapping dazu, ein zweidimensionales Bild (Textur) auf einer Oberfläche abzubilden. Eine weitere Technik ist Bumpmapping, mit dem Oberflächenunebenheiten dargestellt werden können. Spiegelungseffekte lassen sich beim Echtzeitrendern mit Environment Mapping erzielen.
Realistisches Rendern

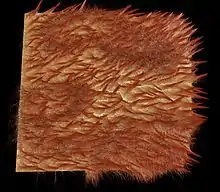
Ob ein gerendertes Bild realistisch wirkt, hängt maßgeblich davon ab, inwieweit die Verteilung des Lichts innerhalb einer Szene simuliert wird. Während beim Shading nur die direkte Beleuchtung berechnet wird, spielt bei der indirekten Beleuchtung die Reflexion von Licht zwischen Objekten eine Rolle. Dadurch werden Effekte wie Räume, die nur durch einen schmalen Lichtspalt insgesamt erhellt werden, möglich. Werden alle Arten der Lichtreflexion berücksichtigt, so spricht man von globaler Beleuchtung. Die globale Beleuchtung muss für ein realistisches Ergebnis berücksichtigt werden und ist bei Echtzeitverfahren nicht oder nur sehr eingeschränkt möglich. Mathematisch wird sie durch die Rendergleichung beschrieben.
Eines der in der realistischen Bildsynthese verwendeten Verfahren ist Raytracing. Raytracing ist zwar in erster Linie ein Algorithmus zur Verdeckungsberechnung, der auf der Aussendung von Strahlen basiert, kann aber in erweiterten Formen auch Lichtreflexionen und -brechungen berechnen. Um die globale Beleuchtung zu simulieren, werden Verfahren wie Path Tracing oder Photon Mapping verwendet, die auf Raytracing basieren.
Ein weiterer Algorithmus der realistischen Bildsynthese ist Radiosity. Er basiert auf der Unterteilung der Oberflächen in kleine Teilflächen, für die die Rendergleichung numerisch gelöst wird. In seiner Grundform ist Radiosity nur auf ideal diffuse Flächen anwendbar. Im Gegensatz zu Raytracing wird die Lichtverteilung unabhängig vom Blickpunkt berechnet. Dadurch eignet sich Radiosity besonders zum Rendern statischer Szenen in Echtzeit, bei denen eine zeitaufwändige Vorausberechnung vertretbar ist.
In der Filmindustrie wird vor allem das REYES-Verfahren verwendet, bei dem die Oberflächen der Szene in sehr kleine Polygone zerlegt werden, für die einzeln die Farbe berechnet wird.
Volumengrafik
Bei der Volumengrafik werden die zu rendernden Objekte nicht als Oberflächen beschrieben, sondern als räumliche Datensätze, sogenannte Voxelgitter. Es handelt sich dabei um gitterförmig angeordnete Werte, die die „Dichte“ eines Objektes an einem bestimmten Punkt beschreiben. Diese Form der Datenrepräsentation ist besonders geeignet für Objekte wie Wolken, die keine klaren Umrisse haben. Zum Rendern von Voxelgittern wurden spezielle Techniken wie Splatting entwickelt. Da viele bildgebende Verfahren Voxeldaten erzeugen, ist die Volumengrafik insbesondere für die Medizin von Bedeutung.
Animation

Die computergestützte Erzeugung von Animationen erfordert Techniken, die über die statische Modellierung und Synthese von Einzelbildern hinausgehen. Viele Computeranimationen basieren auf der Schlüsselbildanimation, bei der nur für einige Einzelbilder Parameter der Szene wie die Position und Form von Objekten oder die Kamerablickrichtung gesetzt werden. Die Werte dieser Parameter werden für die dazwischen liegenden Bilder mit Hilfe geeigneter Splines interpoliert. Auch die Rotation von Objekten kann mit mathematischen Verfahren interpoliert werden.
Oft sind Objekte für die Animation hierarchisch modelliert, sodass sich die Bewegung eines in der Hierarchie höher liegenden Objekts auf alle Unterobjekte auswirkt. Ein Beispiel ist ein Planetensystem, in dem Monde um Planeten und diese wiederum um die Sonne rotieren. Zum Teil werden Objekte ähnlich wie in der Robotik als zusammenhängende Struktur modelliert, deren Einzelteile durch Gelenke miteinander verbunden sind. Derartige Strukturen können unter Anwendung der direkten oder inversen Kinematik animiert werden. Für die Character animation bieten sich auch aufwändigere Motion-Capture-Techniken an.

Die Animation mehrerer Objekte erfordert häufig Techniken zur Kollisionserkennung. Besonders in Computerspielen wird zusätzlich auf die künstliche Intelligenz zurückgegriffen, um im Rahmen der Gruppensimulation Objekte so zu animieren, dass sie ein bestimmtes Ziel ausführen. Bei größeren Gruppen von dutzenden Objekten entsteht oft ein Schwarmverhalten, das mit vergleichsweise einfachen Techniken plausibel simuliert werden kann. Eine noch höhere Anzahl von Objekten kann durch Partikelsysteme beschrieben werden. Dabei werden auf viele Tausend sehr kleine Partikel Kräfte ausgeübt, um Erscheinungen wie Explosionen, Flüssigkeiten, Rauch oder Feuer zu simulieren. Wirklich realistische Ergebnisse lassen sich jedoch nur mit physikalisch basierten Techniken erzielen, bei denen komplexe Berechnungen ausgeführt werden müssen.
Anwendungen

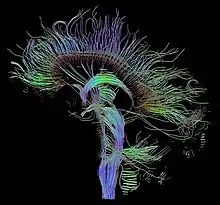
Bildgebung in der Medizin
Eine wichtige Anwendung findet die Computergrafik in der Mensch-Computer-Interaktion, dem Teilgebiet der Informatik, das die benutzergerechte Gestaltung von interaktiven Systemen und ihren Benutzerschnittstellen untersucht. Dieses Gebiet wurde nicht nur deshalb oft mit der Computergrafik zusammen behandelt, weil es sich mit grafischen Benutzeroberflächen oder Prozessvisualisierung befasst, sondern auch, weil Forscher aus dem Bereich der Computergrafik bereits früh Zugang zu damals neuartigen Ein- und Ausgabegeräten hatten.[8] Allgegenwärtig sind Computergrafiken in Form von Präsentationsgrafiken oder in Desktop-Publishing-Dokumenten.
Ein mit der Computergrafik verwandtes, aber abgegrenztes Gebiet ist die Bildverarbeitung. Sie beschäftigt sich mit der Aufbereitung von bereits vorhandenen Bildern, um deren Inhalte automatisch auszuwerten, führt also die umgekehrte Aufgabe der Computergrafik aus. Die Techniken der Bildverarbeitung finden zum Teil auch bei der Bildbearbeitung Anwendung.
Die visuelle digitale Kunst entwickelte sich schon mit Beginn der Computergrafik. Anwendung findet die künstlerische Gestaltung von Computergrafiken in Computerspielen, die immer komplexere 3D-Modelle und fortgeschrittene Renderalgorithmen verwenden. In der Filmtechnik und Werbung kommen fast alle Arten von Computergrafik-Technologien zum Einsatz, um Trickfilme und Computer Generated Imagery zu erzeugen. Viele moderne Filme verwenden digitale Compositing-Techniken, um separat gefilmte Vordergrundszenen über einen Hintergrund zu legen.
CAD nutzt die Computertechnik als „virtuelles Zeichenbrett“, um Maschinenteile und andere Produkte zu entwerfen oder die anschließenden Fertigungsprozesse mittels Computer-aided manufacturing zu steuern. In der Kartografie und in Geoinformationssystemen wird die Computergrafik dazu verwendet, um sowohl präzise als auch schematische Darstellungen aus geografischen und anderen raumbezogenen Messdaten zu erzeugen.
Simulationen und Visualisierungen virtueller Umgebungen reichen von der Architekturdarstellung bis hin zu wissenschaftlichen und sicherheitskritischen Bereichen. Sowohl die virtuelle als auch die erweiterte Realität legen ihr Hauptaugenmerk auf die Interaktion mit dem Betrachter, etwa auf das Verändern der Perspektive bei einer Drehung des Kopfes. Dabei kommen sowohl 3D-Computergrafik als auch hochentwickelte Darstellungstechnologien zum Einsatz. Während in der virtuellen Realität die Welten komplett im Rechner generiert werden, beschäftigt sich die erweiterte Realität mit dem Einbinden von künstlichen Objekten in die Realität, zum Beispiel über Head-Mounted Displays.
In der Medizin werden möglichst aussagekräftige Bilder aus Daten, die durch bildgebende Verfahren gewonnen wurden, generiert. Dies geschieht hauptsächlich mit den Mitteln der Volumengrafik.
Die Computergrafik ist Teil der Studiengänge Computervisualistik, Visual Computing, Medieninformatik und Informatik.
Literatur
Bücher:
- Michael Bender, Manfred Brill: Computergrafik: ein anwendungsorientiertes Lehrbuch. Hanser, München 2006, ISBN 3-446-40434-1.
- Hans-Joachim Bungartz, Michael Griebel, Christoph Zenger: Einführung in die Computergraphik: Grundlagen, geometrische Modellierung, Algorithmen. 2. Auflage. Vieweg, Braunschweig/Wiesbaden 2002, ISBN 3-528-16769-6.
- James Foley, Andries van Dam, Steven K. Feiner, John F. Hughes: Computer Graphics: Principles and Practice. 2. Auflage. Addison-Wesley, Reading 1996, ISBN 0-201-84840-6.
- David Rogers: Procedural Elements for Computer Graphics. WCB/McGraw-Hill, Boston 1998, ISBN 0-07-053548-5.
- Peter Shirley, Michael Gleicher, Stephen R. Marschner, Erik Reinhard, Kelvin Sung, Wiliam B. Thompson, Peter Willemsen: Fundamentals of Computer Graphics. Nr. 2. AK Peters, Wellesley 2005, ISBN 1-56881-269-8.
- Natascha Adamowsky (Hrsg.): Digitale Moderne. Die Modellwelten von Matthias Zimmermann. Hirmer Verlag, München 2018, ISBN 978-3-7774-2388-3
Zeitschriften (Auswahl):
Weblinks
- HyperGraph – Teaching Computer Graphics – Lernmaterialien zu Themen der Computergrafik (englisch)
- A Critical History of Computer Graphics and Animation – Ausführliche Darstellung der Geschichte der Computergrafik (englisch)
- Computergrafik WBT – Web Based Training zum Thema Computergrafik
Einzelnachweise
- James Foley u. a.: Computer Graphics: Principles and Practice. S. 2
- Peter Shirley u. a.: Fundamentals of Computer Graphics. S. 1
- Carl Machover: Four Decades of Computer Graphics. IEEE Computer Graphics and Applications 14, 6 (November 1994): 14–19, hier S. 14, ISSN 0272-1716
- Carl Machover: Four Decades of Computer Graphics. S. 17
- Carl Machover: Four Decades of Computer Graphics. S. 18
- Max Agoston: Computer Graphics and Geometric Modeling: Implementation and Algorithms. Springer, London 2005, ISBN 1-85233-818-0, S. 157.
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. AK Peters, Natick MA 2002, ISBN 1-56881-182-9, S. 7.
- Peter Shirley u. a.: Fundamentals of Computer Graphics. S. 2