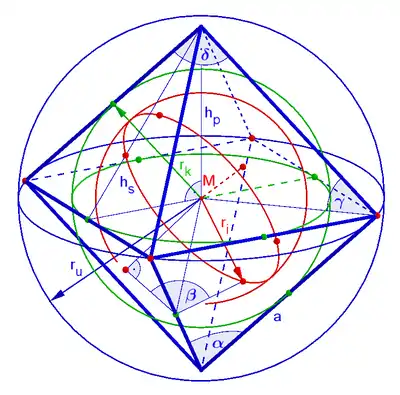
Oktaeder

Das (auch, v. a. österr.: der) Oktaeder [ɔktaˈeːdɐ] (von altgriechisch ὀκτάεδρος oktáedros, deutsch ‚achtseitig‘)[1] ist einer der fünf platonischen Körper, genauer ein regelmäßiges Polyeder (Vielflach, Vielflächner) mit

• 8 kongruenten gleichseitigen Dreiecken als Seitenflächen
• 12 gleich langen Kanten und
• 6 Ecken, in denen jeweils vier Seitenflächen zusammentreffen

Oktaeder
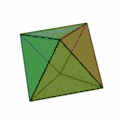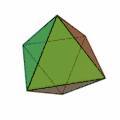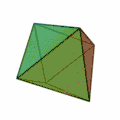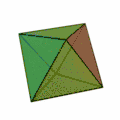Art der Seitenflächen	gleichseitige Dreiecke
Anzahl der Flächen	8
Anzahl der Ecken	6
Anzahl der Kanten	12
Schläfli-Symbol	{3,4}
dual zu	Hexaeder (Würfel)
Körpernetz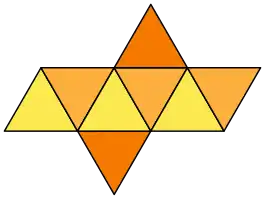
Anzahl verschiedener Netze	11
Anzahl Kanten in einer Ecke	4
Anzahl Ecken einer Fläche	3
Oktaeder im STL-Format

Es ist sowohl eine gleichseitige vierseitige Doppelpyramide mit quadratischer Grundfläche – in seiner Eigenschaft als das regelmäßige Kreuzpolytop der dritten Dimension – als auch ein gleichseitiges Antiprisma mit einem gleichseitigen Dreieck als Grundfläche.

Symmetrie

Drei senkrecht zueinander stehende Quadrate, die jeweils die Grundfläche einer Doppelpyramide bilden.

Oktaeder mit Beispielen der Drehachsen ${\displaystyle C_{4},C_{3},C_{2}}$ und zwei Symmetrieebenen (rot bzw. grün)

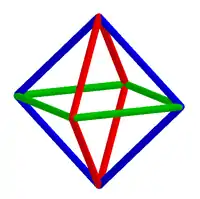
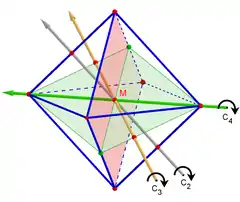
Wegen seiner hohen Symmetrie – alle Ecken, Kanten und Flächen sind untereinander gleichartig – ist das Oktaeder ein reguläres Polyeder. Es hat:

• 3 vierzählige Drehachsen ${\displaystyle C_{4}}$ (durch gegenüberliegende Ecken)
• 4 dreizählige Drehachsen ${\displaystyle C_{3}}$ (durch die Mittelpunkte gegenüberliegender Flächen)
• 6 zweizählige Drehachsen ${\displaystyle C_{2}}$ (durch die Mittelpunkte gegenüberliegender Kanten)
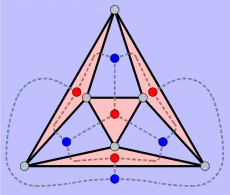
• 9 Symmetrieebenen (3 Ebenen durch je vier Ecken (z. B. rot), 6 Ebenen durch jeweils zwei Ecken und zwei Kantenmittelpunkte (z. B. grün))
• 14 Drehspiegelungen (6 um 90° mit den Ebenen durch je vier Ecken und 8 um 60° mit Ebenen durch je sechs Kantenmitten)

und ist

• punktsymmetrisch zum Mittelpunkt.

Insgesamt hat die Symmetriegruppe des Oktaeders – die Oktaedergruppe oder Würfelgruppe – 48 Elemente.

Beziehungen zu anderen Polyedern

Bild 2: Zwei regelmäßige Tetraeder in einem Würfel einbeschrieben ergeben einen Sterntetraeder

Bild 1: Oktaeder (blau) mit dualem Würfel (grün). Die Mittelpunkte (rot) der regelmäßigen Dreiecke sind die Ecken des Würfels.

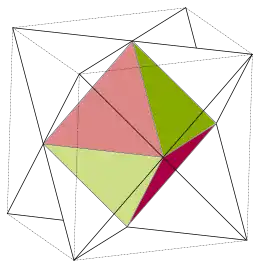
Das Oktaeder ist das zum Hexaeder (Würfel) duale Polyeder (Bild 1) und umgekehrt.

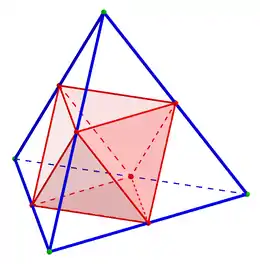
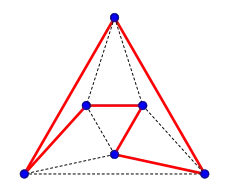
Zwei regelmäßige Tetraeder (siehe Bild 2: ein Tetraeder in Rottönen, das andere in Grüntönen) können in einem Würfel so einbeschrieben werden, dass die Ecken zugleich Würfelecken und die Kanten Diagonalen der Würfelflächen sind. Die Vereinigungsmenge ist ein Sterntetraeder

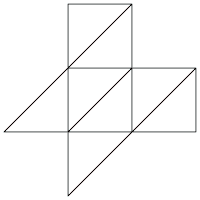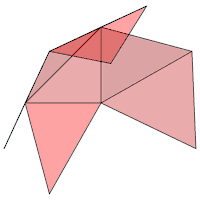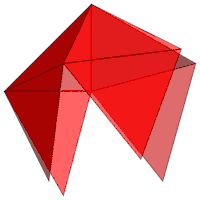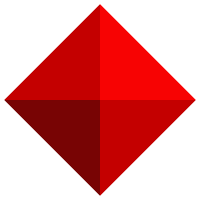
Die dreidimensionale Schnittmenge der zwei Tetraeder (Bild 3) ist ein Oktaeder mit halber Seitenlänge. Setzt man auf die 8 Seitenflächen des Oktaeders Tetraeder auf, entsteht ebenfalls ein Sterntetraeder.

Wird ein Oktaeder von einem regelmäßigen Tetraeder umschrieben (Bild 4), sind die 6 Ecken des Oktaeders die Mittelpunkte der 6 Tetraederkanten und liegen 4 der 8 Oktaederflächen in den Seitenflächen eines der beiden möglichen Tetraeder. Das Oktaeder entsteht also, wenn von einem Tetraeder mit doppelter Kantenlänge 4 Tetraeder mit derselben Seitenlänge abgeschnitten werden.

Mithilfe von Oktaeder und Würfel können zahlreiche Körper konstruiert werden, die ebenfalls die Oktaedergruppe als Symmetriegruppe haben. So erhält man zum Beispiel

• das abgestumpfte Oktaeder mit 8 Sechsecken und 6 Quadraten
• das Kuboktaeder mit 8 Dreiecken und 6 Quadraten, also mit 14 Flächen, und 12 Ecken
• den abgestumpften Würfel mit 8 Dreiecken und 6 Achtecken

als Durchschnitte eines Oktaeders mit einem Würfel (siehe archimedische Körper) und

• das Rhombendodekaeder mit 8 + 6 = 14 Ecken und 12 Rauten als Flächen

als konvexe Hülle einer Vereinigung eines Oktaeders mit einem Würfel.

Bild 3: Zwei Tetraeder im Würfel haben als dreidimensionale Schnittmenge ein Oktaeder mit halber Seitenlänge.

Bild 4: Ein regelmäßiges Tetraeder mit doppelter Seitenlänge umschreibt ein Oktaeder. Die 6 Ecken des Oktaeders sind dann die Mittelpunkte der 6 Tetraederkanten.

Formeln

Die folgende Tabelle ist eine Zusammenstellung von metrischen Eigenschaften eines regulären Oktaeders, die im nächsten Abschnitt hergeleitet werden.

Größen eines Oktaeders mit Kantenlänge a
Volumen	${\displaystyle V={\frac {\sqrt {2}}{3}}\;a^{3}\approx 0{,}471\cdot a^{3}}$	ohne Raumwinkel ${\displaystyle \Omega }$ in den Ecken
Oberflächeninhalt	${\displaystyle A_{O}=2{\sqrt {3}}\;a^{2}\approx 3{,}464\cdot a^{2}}$
Umkugelradius	${\displaystyle r_{u}={\frac {a}{\sqrt {2}}}\approx 0{,}707\cdot a}$
Kantenkugelradius	${\displaystyle r_{k}={\frac {a}{2}}=0{,}5\cdot a}$
Inkugelradius	${\displaystyle r_{i}={\frac {a}{\sqrt {6}}}\approx 0{,}408\cdot a}$
Verhältnis von Volumen  zu Umkugelvolumen	${\displaystyle {\frac {V}{V_{UK}}}={\frac {1}{\pi }}\approx 0{,}318}$
Innenwinkel des gleichseitigen Dreiecks	${\displaystyle \alpha =60^{\circ }}$
Winkel zwischen benachbarten Flächen	${\displaystyle \beta =2\arctan {\sqrt {2}}\approx 109{,}47^{\circ }}$
Winkel zwischen Kante und Fläche	${\displaystyle \gamma =\arctan {\sqrt {2}}\approx 54{,}73^{\circ }}$
Raumwinkel in den Ecken	${\displaystyle \Omega =8\arctan {\sqrt {2}}-2\pi \approx 1{,}35935\,\mathrm {sr} }$
Sphärizität	${\displaystyle \Psi ={\sqrt[{3}]{\frac {\pi }{3{\sqrt {3}}}}}\approx 0{,}846}$

Flächen, Winkel, Radien, Koordinaten

Punkte des Oktaeders

regul. Oktaeder

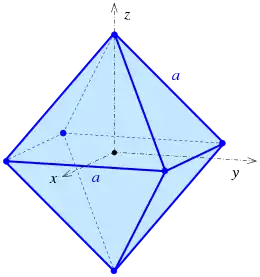
Ein Oktaeder mit der Kantenlänge ${\displaystyle a}$ kann man sich aus zwei quadratischen Pyramiden mit der Quadratlänge und der Seitenkantenlänge gleich ${\displaystyle a}$ zusammengesetzt denken. Wendet man den Satz von Pythagoras auf die Höhe ${\displaystyle h}$ , eine halbe Diagonale der Grundfläche und eine Seitenkante an, ergibt sich

${\displaystyle h={\frac {a}{\sqrt {2}}}}$.

Damit lassen sich die Punkte eines regulären Oktaeders mit der Kantenlänge ${\displaystyle a}$ in einem kartesischen Koordinatensystem so beschreiben:

• ${\displaystyle \left(\pm {\frac {a}{2}},\pm {\frac {a}{2}},0\right),\ \left(0,0,\pm {\frac {a}{\sqrt {2}}}\right)}$

Winkel

Aus der Zeichnung erkennt man, dass für den Winkel ${\displaystyle \gamma }$ zwischen einer Seitenfläche und einer Kante ${\displaystyle \ \tan \gamma ={\frac {h}{\frac {a}{2}}}={\sqrt {2}}\ }$ gilt. Also ist der

regul. Oktaeder: Eigenschaften

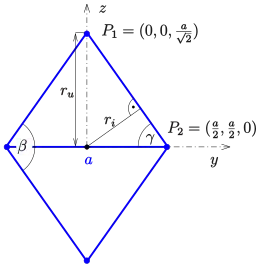
• Winkel zwischen einer Kante und einer Seitenfläche gleich

${\displaystyle \gamma =\arctan {\sqrt {2}}\approx 54{,}73^{\circ }}$

und der

• Winkel zwischen zwei Seitenflächen ist

${\displaystyle \beta =2\gamma \approx 109{,}47^{\circ }}$

Um/In/Kanten-Kugelradien

Die Kugel, die die Kanten des Oktaeders berührt, berührt das Basisquadrat der Pyramide von innen. Also ist der

• Kantenkugelradius ${\displaystyle \ r_{k}={\frac {a}{2}}=0{,}5\;a}$

Die Umkugel geht durch alle Oktaederpunkte und es ist der

• Umkugelradius ${\displaystyle \ r_{u}=h={\frac {a}{\sqrt {2}}}\approx 0{,}71\;a}$

Der Inkugelradius ist (im Bild) der Abstand des Nullpunktes zur Gerade in der y-z-Ebene durch die Punkte ${\displaystyle \left(0,{\frac {a}{\sqrt {2}}}\right),\left({\frac {a}{2}},0\right)}$ . Sie hat die Gleichung ${\displaystyle 2y+{\sqrt {2}}z-a=0}$. Berechnet man den Abstand mit Hilfe der Hessesche Normalform ergibt sich der

• Innenkugelradius ${\displaystyle \ r_{i}={\frac {a}{\sqrt {6}}}\approx 0{,}41\;a}$

Oberfläche, Volumen

Die Oberfläche des Oktaeders ist die Summe der 8 Dreiecksflächen. Die Fläche eines relmäßigen 3-Ecks ist ${\displaystyle A_{3}={\tfrac {\sqrt {3}}{4}}\;a^{2}\ }$. Damit ist die

• Oberfläche des Oktaeders: ${\displaystyle \ A_{O}=2{\sqrt {3}}\;a^{2}}$.

Das Volumen des Oktaeders ist die Summe der Volumina der 2 quadratischen Pyramiden. Das Volumen einer Pyramide ist ${\displaystyle {\tfrac {h}{3}}a^{2}={\tfrac {a^{3}}{3{\sqrt {2}}}}}$ und das

• Volumen des Oktaeders ist ${\displaystyle \ V={\frac {\sqrt {2}}{3}}\;a^{3}}$.

Raumwinkel in den Ecken

Oktaeder mit Einheitskugel

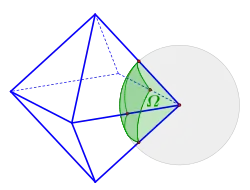
Der Raumwinkel ${\displaystyle \Omega }$ ist der Flächeninhalt des in dem Bild durch rote Punkte markierten sphärischen Vierecks der Einheitskugel in der Oktaederecke. Betrachtet man nur die obere Hälfte (Pyramide) des Oktaeders, so erhält man ein shärisches Dreieck, dessen Winkel in den unteren Punkten jeweils gleich dem halben Winkel ${\displaystyle \gamma }$ zwischen Seitenflächen des Okteders ist (siehe Bild oben). Der Winkel im oberen Punkt ist gleich dem Winkel ${\displaystyle \beta =2\gamma }$. Damit hat das sphärische Dreieck den Flächeninhalt

Raumwinkel

${\displaystyle A_{3}=\gamma +\gamma +2\gamma -\pi =4\gamma -\pi }$.

Der Raumwinkel ${\displaystyle \Omega }$ ist der Flächeninhalt des sphärischen Vierecks:

• ${\displaystyle \Omega =2A_{3}=8\gamma -2\pi =8\arctan {\sqrt {2}}-2\pi \approx 1{,}35935\,\mathrm {sr} }$.

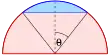
Der Raumwinkel entspricht der Fläche eines Kugelsegments auf der Einheitskugel mit einem halben Öffnungswinkel ${\displaystyle \theta \approx 38{,}4^{\circ }}$

Definition als Menge von Punkten

Das Oktaeder kann als Menge von Punkten im dreidimensionalen euklidischen Raum definiert werden, wo die Summe der absoluten Beträge der 3 Koordinaten im kartesischen Koordinatensystem höchstens so groß ist wie der Umkugelradius ${\displaystyle r_{u}={\tfrac {a}{\sqrt {2}}}}$. Formal lässt sich diese Menge aufschreiben als

${\displaystyle \left\{x\in \mathbb {R} ^{3}\mid \left\|x\right\|_{1}\leq r_{u}\right\}=\left\{(x_{1},x_{2},x_{3})\mid \left\vert x_{1}\right\vert +\left\vert x_{2}\right\vert +\left\vert x_{3}\right\vert \leq r_{u}\right\}}$

Dabei ist ${\displaystyle \left\|x\right\|_{1}}$ die Betragssummennorm oder 1-Norm des Vektors ${\displaystyle x}$. Für das Innere des Oktaeders gilt ${\displaystyle \left\|x\right\|_{1}<r_{u}}$ und für die Oberfläche gilt ${\displaystyle \left\|x\right\|_{1}=r_{u}}$. Nach dieser Definition ist der Mittelpunkt des Oktaeders der Koordinatenursprung und seine Ecken ${\displaystyle (r_{u},0,0)}$, ${\displaystyle (-r_{u},0,0)}$, ${\displaystyle (0,r_{u},0)}$, ${\displaystyle (0,-r_{u},0)}$, ${\displaystyle (0,0,r_{u})}$, ${\displaystyle (0,0,-r_{u})}$ liegen auf den 3 Achsen des kartesischen Koordinatensystems.

Allgemeiner kann ein Oktaeder, das eine beliebige Lage im dreidimensionalen euklidischen Raum hat, mithilfe von Vektoren definiert werden. Ist ${\displaystyle {\vec {m}}}$ der Ortsvektor des Mittelpunkts und sind ${\displaystyle {\vec {u}}}$, ${\displaystyle {\vec {v}}}$, ${\displaystyle {\vec {w}}}$ orthogonale Richtungsvektoren, die den Mittelpunkt des Oktaeders mit 3 Ecken verbinden, also ein Orthogonalsystem des dreidimensionalen Vektorraums ${\displaystyle \mathbb {R} ^{3}}$, dann lässt sich die Menge der Punkte des Oktaeders definieren als die Menge der Vektoren[2]

${\displaystyle \left\{{\vec {m}}+t_{1}\cdot {\vec {u}}+t_{2}\cdot {\vec {v}}+t_{3}\cdot {\vec {w}}\in \mathbb {R} ^{3}\mid \left\|t\right\|_{1}\leq r_{u}\right\}=\left\{{\vec {m}}+t_{1}\cdot {\vec {u}}+t_{2}\cdot {\vec {v}}+t_{3}\cdot {\vec {w}}\in \mathbb {R} ^{3}\mid \left\vert t_{1}\right\vert +\left\vert t_{2}\right\vert +\left\vert t_{3}\right\vert \leq r_{u}\right\}}$

Verallgemeinerung

Die Analoga des Oktaeders in beliebiger Dimension ${\displaystyle n}$ werden als ${\displaystyle n}$-dimensionale Kreuzpolytope bezeichnet und sind ebenfalls reguläre Polytope. Das ${\displaystyle n}$-dimensionale Kreuzpolytop hat ${\displaystyle 2\cdot n}$ Ecken und wird von ${\displaystyle 2^{n}}$ ${\displaystyle n-1}$-dimensionalen Simplexen (als Facetten) begrenzt. Das vierdimensionale Kreuzpolytop hat 8 Ecken, 24 gleich lange Kanten, 32 gleichseitige Dreiecke als Seitenflächen und 16 Tetraeder als Facetten. Das eindimensionale Kreuzpolytop ist eine Strecke, das zweidimensionale Kreuzpolytop ist das Quadrat, das dreidimensionale Kreuzpolytop ist das Oktaeder.

Ein Modell für das ${\displaystyle n}$-dimensionale Kreuzpolytop ist die Einheitskugel bezüglich der Summennorm

${\displaystyle \left\|x\right\|_{1}=\left\vert x_{1}\right\vert +\cdots +\left\vert x_{n}\right\vert }$ für ${\displaystyle x=(x_{1},\dots ,x_{n})\in \mathbb {R} ^{n}}$

im Vektorraum ${\displaystyle \mathbb {R} ^{n}}$. Und zwar ist das (abgeschlossene) Kreuzpolytop daher

• die Menge

${\displaystyle \left\{x\in \mathbb {R} ^{n}\mid \left\|x\right\|_{1}\leq 1\right\}=\left\{(x_{1},\dots ,x_{n})\mid \left\vert x_{1}\right\vert +\cdots +\left\vert x_{n}\right\vert \leq 1\right\}}$.

• die konvexe Hülle der ${\displaystyle 2\cdot n}$ Eckpunkte ${\displaystyle \pm e_{i}}$, wobei ${\displaystyle e_{i}}$ die Einheitsvektoren sind.
• der Durchschnitt der ${\displaystyle 2^{n}}$ Halbräume, die durch die Hyperebenen der Form

${\displaystyle \pm x_{1}\pm \cdots \pm x_{n}=1}$

bestimmt werden und den Ursprung enthalten.

Das Volumen des ${\displaystyle n}$-dimensionalen Kreuzpolytops beträgt ${\displaystyle {\tfrac {(2\cdot r)^{n}}{n!}}}$, wobei ${\displaystyle r>0}$ der Radius der Kugel um den Koordinatenursprung bezüglich der Summennorm ist. Die Beziehung lässt sich mittels Rekursion und dem Satz von Fubini beweisen.[3]

Netze des Oktaeders

Das Oktaeder hat elf Netze[4]. Das heißt, es gibt elf Möglichkeiten, ein hohles Oktaeder durch Aufschneiden von 5 Kanten aufzuklappen und in der Ebene auszubreiten. Die anderen 7 Kanten verbinden jeweils die 8 gleichseitigen Dreiecke des Netzes. Um ein Oktaeder so zu färben, dass keine benachbarten Flächen dieselbe Farbe haben, braucht man mindestens 2 Farben.

Ein Netz des Oktaeders

Animation eines Oktaedernetzes

Graphen, duale Graphen, Zyklen, Färbungen

Färbungen veranschaulicht
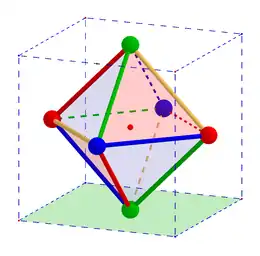
Oktaeder einbeschrieben vom dualen Würfel

Das Oktaeder hat einen ihm zugeordneten ungerichteten planaren Graphen mit 6 Knoten, 12 Kanten und 8 Gebieten, der 4-regulär ist, d. h. von jedem Knoten gehen 4 Kanten aus, sodass der Grad für alle Knoten gleich 4 ist. Bei planaren Graphen ist die genaue geometrische Anordnung der Knoten unwesentlich. Wichtig ist allerdings, dass sich die Kanten nicht schneiden müssen. Die Knoten dieses Oktaedergraphen entsprechen den Ecken des Würfel.

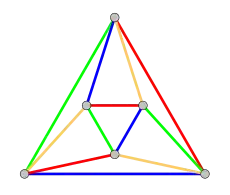
Die Knoten des Oktaedergraphen können mit 3 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind. Dies bedeutet, dass die chromatische Zahl dieses Graphen gleich 3 ist. Außerdem können die Kanten mit 4 Farben so gefärbt werden, dass benachbarte Kanten immer unterschiedlich gefärbt sind. Mit 3 Farben ist das nicht möglich, sodass der chromatische Index für die Kantenfärbung gleich 4 ist (das nebenstehende Bild veranschaulicht diese Färbungen).

Um die entsprechende nötige Anzahl der Farben für die Flächen oder Gebiete zu bestimmen, ist der duale Graph (Würfelgraph) mit 8 Knoten, 12 Kanten und 6 Gebieten hilfreich. Die Knoten dieses Graphen werden dabei den Gebieten des Oktaedergraphen eineindeutig (bijektiv) zugeordnet und umgekehrt (siehe bijektive Funktion und Abbildung oben). Die Knoten des Würfelgraphen können mit 2 Farben so gefärbt werden, dass benachbarte Knoten immer unterschiedlich gefärbt sind, sodass die chromatische Zahl des Würfelgraphen gleich 2 ist. Daraus lässt sich indirekt schließen: Weil die chromatische Zahl gleich 2 ist, sind 2 Farben für eine solche Flächenfärbung des Oktaeders oder eine Färbung der Gebiete des Oktaedergraphen nötig.[5]

Knotenfärbung des Oktaedergraphen

Kantenfärbung des Oktaedergraphen

Flächenfärbung des Oktaedergraphen mit dualer Knotenfärbung des Würfelgraphen

Die 5 aufgeschnittenen Kanten jedes Netzes (siehe oben) bilden zusammen mit den Ecken (Knoten) einen Spannbaum des Oktaedergraphen. Jedes Netz entspricht genau einem Spannbaum und umgekehrt, sodass hier eine eineindeutige (bijektive) Zuordnung zwischen Netzen und Spannbäumen besteht. Wenn man ein Oktaedernetz ohne das äußere Gebiet als Graphen betrachtet, erhält man als dualen Graphen jeweils einem Baum mit 8 Knoten und 7 Kanten und dem maximalen Knotengrad 3. Jede Fläche des Oktaeders wird dabei einem Knoten des Baums zugeordnet. Dabei kommt nicht jede graphentheoretische Konstellation (siehe Isomorphie von Graphen) solcher Bäume vor, aber einige mehrfach.

Der Oktaedergraph besitzt 32 Hamiltonkreise und 1488 Eulerkreise.[6]

Oktaedergraph mit einem der 32 Hamiltonkreise

Raumfüllungen mit Oktaedern

Der dreidimensionale euklidische Raum kann lückenlos mit platonischen Körpern oder archimedischen Körpern gleicher Kantenlänge ausgefüllt werden kann. Solche dreidimensionalen Parkettierungen werden Raumfüllung genannt. Die folgenden Raumfüllungen enthalten Oktaeder:

• 
  Raumfüllung mit Oktaeder und Tetraeder
• 
  Raumfüllung mit Kuboktaeder und Oktaeder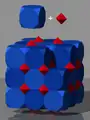
• 
  Raumfüllung mit Hexaederstumpf und Oktaeder

Sierpinski-Tetraeder

→ Hauptartikel: Sierpinski-Tetraeder

Das Sierpinski-Tetraeder. Die Anzahl der Teil-Tetraeder vervierfacht sich mit jedem Iterationsschritt, das Volumen geht gegen 0, der Flächeninhalt der Oberfläche bleibt konstant.
Die herausgeschnittenen Hohlräume (Polyeder) sind Oktaeder verschiedener Seitenlänge.

Das Oktaeder steht indirekt im Zusammenhang mit dem Sierpinski-Tetraeder. Das Sierpinski-Tetraeder ist die dreidimensionale Verallgemeinerung des Sierpinski-Dreiecks. Die Startfigur ist ein Tetraeder. Aus dessen Mitte wird in jedem Iterationsschritt ein Oktaeder mit halber Kantenlänge herausgeschnitten. Übrig bleiben 4 Tetraeder, aus denen wieder je ein Oktaeder herausgeschnitten wird usw.[7][8]

Nach dem Iterationsschritt ${\displaystyle k}$ sind offensichtlich ${\displaystyle 4^{k}}$ Teil-Tetraeder mit derselben Seitenlänge entstanden. Die Anzahl der herausgeschnittenen Oktaeder mit verschiedener Seitenlänge beträgt ${\displaystyle {\frac {4^{k}-1}{3}}}$.

Die Dimension für dieses Gebilde ist ${\displaystyle D={\frac {\log(4)}{\log(2)}}=2}$, obwohl es sich hierbei um eine Figur im dreidimensionalen Raum handelt. Mit einer zunehmenden Zahl von Iterationsschritten geht das Volumen der Figur gegen 0, der Flächeninhalt der Oberfläche bleibt jedoch konstant, weil sich die Anzahl der Seitenflächen der zueinander deckungsgleichen Teil-Tetraeder mit jedem Iterationsschritt vervierfacht, während sich die Seitenlänge dieser Seitenflächen, die alle deckungsgleiche Dreiecke sind, halbiert.

Anwendungen

Oktaedrische Alaunkristalle

In der Chemie können sich bei der Vorhersage von Molekülgeometrien nach dem VSEPR-Modell oktaedrische Moleküle ergeben. Auch in Kristallstrukturen, wie der kubisch flächenzentrierten Natriumchlorid-Struktur (Koordinationszahl 6), taucht das Oktaeder in der Elementarzelle auf, genauso in der Komplexchemie, falls sich 6 Liganden um ein Zentralatom lagern.

Einige in der Natur vorkommende Minerale, z. B. das Alaun, kristallisieren in oktaedrischer Form aus.

In Rollenspielen werden oktaedrische Spielewürfel verwendet und dort als „W8“, also als Würfel mit 8 Flächen, bezeichnet.

Siehe auch

• Oktaederzahlen
• Diederwinkel
• Polyeder
• Platonischer Körper

Weblinks

• Euklid: Stoicheia. Buch XIII.14. Oktaeder einer Kugel ...
• Oktaeder. – Mathematische Basteleien

Einzelnachweise

1. Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914 (zeno.org [abgerufen am 12. März 2020]).
2. Susumu Onaka, Department of Materials Science and Engineering, Tokyo Institute of Technology: Simple equations giving shapes of various convex polyhedra: the regular polyhedra and polyhedra composed of crystallographically low-index plane
3. Martin Henk, Jürgen Richter-Gebert, Günter M. Ziegler, Technische Universität Berlin: Basic properties of convex polytopes
4. Eric Weisstein: Regular Oktahedron. Netze. In: MathWorld Wolfram. A Wolfram Web Resource, abgerufen am 27. Juni 2020.
5. Mike Zabrocki: HOMEWORK #3 SOLUTIONS - MATH 3260. (PDF) York University, Mathematics and Statistics, Toronto, 2003, S. 3, abgerufen am 31. Mai 2020.
6. Eric Weisstein: Octahedral Graph. In: MathWorld Wolfram. A Wolfram Web Resource, abgerufen am 27. Juni 2020.
7. Wolfram MathWorld: Tetrix
8. Gayla Chandler, Hideki Tsuiki: Photographs: Sierpinski Tetrahedron and its Complement