Drehung
Unter einer Drehung versteht man in der Geometrie eine Selbstabbildung des euklidischen Raumes mit mindestens einem Fixpunkt, die alle Abstände invariant lässt und die Orientierung erhält. Wird die Orientierung vertauscht, so liegt eine Spiegelung (Geometrie) oder Drehspiegelung vor.
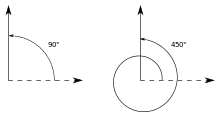
Da Drehungen Längen (und folglich Winkel) invariant lassen, ist jede Drehung eine Kongruenzabbildung. Im zwei- und dreidimensionalen Raum gehört zu jeder Drehung ein bestimmter Drehwinkel. Drehungen, deren Drehwinkel sich um 360° oder ein Vielfaches davon unterscheiden, sind identisch.
In der Ebene lässt jede echte Drehung (d. h. nicht die Drehung um den Winkel null) nur einen Punkt fest, das Drehzentrum. Ist ein von verschiedener Punkt und sein Bild, dann hängt der Winkel nicht von ab und definiert den Drehwinkel. Eine Drehung um 180° bewirkt dieselbe Abbildung der Ebene wie eine Punktspiegelung am Drehzentrum .
Im dreidimensionalen Raum lässt jede echte Drehung genau eine Gerade fest, die Drehachse. Jede zur Drehachse senkrechte Ebene wird durch die Drehung um denselben Drehwinkel gedreht, wobei ihr Schnittpunkt mit der Achse der Fixpunkt ist.
In der analytischen Geometrie sind Drehungen spezielle längentreue affine Abbildungen. Wählt man ein kartesisches Koordinatensystem, dessen Ursprung auf der Drehachse liegt, so wird der translatorische Anteil Null. Die Drehung wird dann durch eine Drehmatrix beschrieben. In homogenen Koordinaten lässt sich auch eine Drehung mit Translationsanteil als Matrix beschreiben.