Bild (Mathematik)

Bei einer mathematischen Funktion ${\displaystyle f}$ ist das Bild, die Bildmenge oder der Bildbereich einer Teilmenge ${\displaystyle M}$ des Definitionsbereichs die Menge der Werte aus der Zielmenge ${\displaystyle Y}$, die ${\displaystyle f}$ auf ${\displaystyle M}$ tatsächlich annimmt.[1]

Das Bild dieser Funktion ist
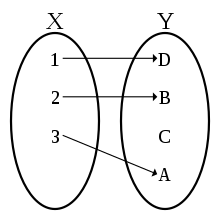
{A, B, D}

Häufig werden dafür auch die Wörter Wertemenge[2] oder Wertebereich[1] benutzt, die aber bei anderen Autoren zur Bezeichnung der ganzen Zielmenge ${\displaystyle Y}$[3] verwendet werden.

Definition

Üblichste Notation

Für eine Funktion ${\displaystyle f\colon X\to Y}$ und eine Teilmenge ${\displaystyle M}$ von ${\displaystyle X}$ bezeichnet man die folgende Menge als das Bild von M unter f:

${\displaystyle f(M):=\{f(x)\mid x\in M\}}$

Das Bild von f ist dann das Bild der Definitionsmenge unter ${\displaystyle f}$, also:

${\displaystyle \operatorname {Bild} (f):=f(X)}$

Im Allgemeinen n​utzt man d​ie übliche Mengennotation, u​m die Bildmenge darzustellen, i​n obigem Beispiel:

${\displaystyle \mathrm {Bild} (f)=\{A,B,D\}}$

Alternative Notationen

• Für ${\displaystyle f(M)}$ wird auch die Notation ${\displaystyle f[M]}$ verwendet, um kenntlich zu machen, dass ${\displaystyle f}$ nicht auf ${\displaystyle M}$ als Ganzem, sondern elementweise auf die Mitglieder dieser Menge anzuwenden ist. Als weitere Bezeichnungsweise kommt gelegentlich ${\displaystyle f''M}$ vor.[4][5]

• Für ${\displaystyle \operatorname {Bild} (f)}$ ist auch die englische Bezeichnung ${\displaystyle \operatorname {im} f}$ („im“ vom englischen Wort image) gebräuchlich.

Beispiele

Wir betrachten die Funktion ${\displaystyle f\colon \mathbb {Z} \to \mathbb {Z} }$ (ganze Zahlen) mit ${\displaystyle f(x):=x^{2}}$.

• Hierbei werden verschiedene Eingabemengen nicht unbedingt auf verschiedene Bildmengen geschickt:

${\displaystyle f(\{1,2,3\})=\{1,4,9\}\ }$

${\displaystyle f(\{-3,-2,-1\})=\{1,4,9\}\ }$

${\displaystyle f(\{-3,-2,-1,1,2,3\})=\{1,4,9\}\ }$

• Insgesamt ist die Menge der Quadratzahlen das Bild der Funktion:

${\displaystyle \operatorname {Bild} (f)=\{0,1,4,9,16,25,36,49,\dotsc \}\ }$

Eigenschaften

Es sei ${\displaystyle f\colon X\to Y}$ eine Funktion und ${\displaystyle M}$ und ${\displaystyle N}$ seien Teilmengen von ${\displaystyle X}$:

• ${\displaystyle f(\varnothing )=\varnothing }$
• ${\displaystyle M\subseteq N\implies f(M)\subseteq f(N)}$
• ${\displaystyle f}$ ist genau dann surjektiv, wenn ${\displaystyle \operatorname {Bild} (f)=Y}$.
• ${\displaystyle f(M\cup N)=f(M)\cup f(N)}$
• ${\displaystyle f(M\cap N)\subseteq f(M)\cap f(N)}$
  Ist ${\displaystyle f}$ injektiv, dann gilt hier ebenfalls die Gleichheit.

Die Aussagen über Vereinigung u​nd Durchschnitt lassen s​ich von z​wei Teilmengen a​uf beliebige nichtleere Familien v​on Teilmengen verallgemeinern.[6]

Siehe auch

• Bild (Kategorientheorie)
• Homomorphiesatz
• Kern (Algebra)
• Urbild (Mathematik)

Einzelnachweise

1. Harro Heuser: Lehrbuch der Analysis. Teil 1. 8., überarbeitete Auflage. B. G. Teubner, Stuttgart 1990, ISBN 3-519-12231-6, S. 106.
2. Reinhard Dobbener: Analysis. Studienbuch für Ökonomen. 4., korrigierte Auflage. Oldenbourg Wissenschaftsverlag, München u. a. 2007, ISBN 978-3-486-57999-4, S. 12, Definition 1.12.
3. Michael Ruzicka, Lars Diening: Analysis I. Vorlesung vom Wintersemester 2004/2005. (Memento vom 23. Januar 2005 im Internet Archive). S. 21. (Memento vom 21. Oktober 2013 im Internet Archive) (PDF; 74 kB).
4. Jean E. Rubin: Set Theory for the Mathematician. Holden-Day, 1967, S. xix.
5. M. Randall Holmes: Inhomogeneity of the urelements in the usual models of NFU. 29. Dezember 2005, auf: Semantic Scholar. S. 2.
6. Beweise im Beweisarchiv