Komplexe Zahl

Die komplexen Zahlen stellen eine Erweiterung der reellen Zahlen dar. Ziel der Erweiterung ist es, algebraische Gleichungen wie ${\displaystyle x^{2}+1=0}$ bzw. ${\displaystyle x^{2}=-1}$ lösbar zu machen. Im Gegensatz zu den Erweiterungen ${\displaystyle \mathbb {N} \rightarrow \mathbb {Z} \rightarrow \mathbb {Q} \rightarrow \mathbb {R} }$ reicht es hier nicht mehr aus, die Zahlen „linksseitig“ zu erweitern (ganze Zahlen) oder „dichter zu stopfen“ (rationale und reelle Zahlen), sondern man wechselt von einer Zahlengeraden zu einer Zahlenebene.

${\displaystyle \mathbb {C} }$

Der Buchstabe C mit Doppelstrich
steht für die Menge der komplexen Zahlen

Die komplexen Zahlen ${\displaystyle \mathbb {C} }$ beinhalten die reellen Zahlen ${\displaystyle \mathbb {R} }$, die die rationalen Zahlen ${\displaystyle \mathbb {Q} }$ beinhalten, zu denen wiederum die ganzen Zahlen ${\displaystyle \mathbb {Z} }$ und die natürlichen Zahlen ${\displaystyle \mathbb {N} }$ gehören.

Da die Quadrate aller reellen Zahlen größer oder gleich 0 sind, kann die Lösung von Gleichungen ${\displaystyle x^{2}=-1}$ keine reelle Zahl sein. Man braucht eine ganz neue Zahl, die man üblicherweise ${\displaystyle \mathrm {i} }$ nennt, mit der Eigenschaft ${\displaystyle \mathrm {i} ^{2}=-1\ }$. Diese Zahl ${\displaystyle \mathrm {i} }$ wird als imaginäre Einheit bezeichnet.

Komplexe Zahlen werden nun als Summe ${\displaystyle a+b\cdot \mathrm {i} }$ definiert, wobei ${\displaystyle a}$ und ${\displaystyle b}$ reelle Zahlen sind und ${\displaystyle \mathrm {i} }$ die oben definierte imaginäre Einheit ist. Auf die so definierten komplexen Zahlen lassen sich die üblichen Rechenregeln für reelle Zahlen anwenden, wobei ${\displaystyle \mathrm {i} }$ wie eine Konstante verwendet wird und ${\displaystyle \mathrm {i} ^{2}}$ durch ${\displaystyle -1}$ ersetzt werden kann und umgekehrt. Für die Menge der komplexen Zahlen wird das Symbol ${\displaystyle \mathbb {C} }$ (ℂ als Unicode-Zeichen U+2102, siehe Buchstaben mit Doppelstrich) verwendet.

Der s​o konstruierte Zahlenbereich d​er komplexen Zahlen bildet e​inen Erweiterungskörper d​er reellen Zahlen u​nd hat e​ine Reihe vorteilhafter Eigenschaften, d​ie sich i​n vielen Bereichen d​er Natur- u​nd Ingenieurwissenschaften a​ls äußerst nützlich erwiesen haben. Einer d​er Gründe für d​iese positiven Eigenschaften i​st die algebraische Abgeschlossenheit d​er komplexen Zahlen. Dies bedeutet, d​ass jede algebraische Gleichung positiven Grades über d​en komplexen Zahlen e​ine Lösung besitzt, w​as für reelle Zahlen n​icht gilt. Diese Eigenschaft i​st der Inhalt d​es Fundamentalsatzes d​er Algebra. Ein weiterer Grund i​st ein Zusammenhang zwischen trigonometrischen Funktionen u​nd der Exponentialfunktion (Eulerformel), d​er über d​ie komplexen Zahlen hergestellt werden kann. Ferner i​st jede a​uf einer offenen Menge einmal komplex differenzierbare Funktion d​ort auch beliebig oft differenzierbar – anders a​ls in d​er Analysis d​er reellen Zahlen. Die Eigenschaften v​on Funktionen m​it komplexen Argumenten s​ind Gegenstand d​er Funktionentheorie, a​uch komplexe Analysis genannt.

In der Elektrotechnik wird stattdessen der Buchstabe ${\displaystyle \mathrm {j} }$ verwendet, um einer Verwechslung mit einer (durch ${\displaystyle i}$ oder ${\displaystyle i(t)}$ bezeichneten) von der Zeit ${\displaystyle t}$ abhängigen Stromstärke vorzubeugen, allerdings erhöht dies die Verwechslungsgefahr mit der Stromdichte ${\displaystyle {\vec {\jmath }}}$ in der Elektrodynamik.

Definition

Die komplexen Zahlen lassen s​ich als Zahlbereich i​m Sinne e​iner Menge v​on Zahlen, für d​ie die Grundrechenarten Addition, Multiplikation, Subtraktion u​nd Division erklärt sind, m​it den folgenden Eigenschaften definieren:

• Die reellen Zahlen sind in den komplexen Zahlen enthalten. Das heißt, dass jede reelle Zahl eine komplexe Zahl ist.
• Das Assoziativgesetz und das Kommutativgesetz gelten für die Addition und die Multiplikation komplexer Zahlen.
• Das Distributivgesetz gilt.
• Für jede komplexe Zahl ${\displaystyle z}$ existiert eine komplexe Zahl ${\displaystyle -z}$, sodass ${\displaystyle z+(-z)=0}$.
• Für jede von Null verschiedene komplexe Zahl ${\displaystyle z}$ existiert eine komplexe Zahl ${\displaystyle {\tfrac {1}{z}}}$ , sodass ${\displaystyle z\cdot {\tfrac {1}{z}}=1}$.
• Es existiert eine komplexe Zahl ${\displaystyle \mathrm {i} }$ mit der Eigenschaft ${\displaystyle \ \mathrm {i} ^{2}=-1}$.
• Unter allen Zahlbereichen mit den zuvor genannten Eigenschaften sind die komplexen Zahlen minimal.

Die letzte Forderung ist gleichbedeutend damit, dass sich jede komplexe Zahl in der Form ${\displaystyle a+b\cdot \mathrm {i} }$ (bzw. in verkürzter Notation ${\displaystyle a+b\,\mathrm {i} }$ oder auch ${\displaystyle a+\mathrm {i} \,b}$) mit reellen Zahlen ${\displaystyle a}$ und ${\displaystyle b}$ darstellen lässt. Die imaginäre Einheit ${\displaystyle \mathrm {i} }$ ist dabei keine reelle Zahl. Die Existenz eines solchen Zahlbereichs wird im Abschnitt zur Konstruktion der komplexen Zahlen nachgewiesen.

Unter Verwendung der Begriffe Körper und Isomorphie lässt sich das so formulieren: Es gibt minimale Körper, die den Körper der reellen Zahlen und ein Element ${\displaystyle \mathrm {i} }$ mit der Eigenschaft ${\displaystyle \mathrm {i} ^{2}=-1}$ enthalten. In einem solchen Körper hat jedes Element ${\displaystyle z}$ eine und nur eine Darstellung als ${\displaystyle z=a+b\,\mathrm {i} }$ mit reellen ${\displaystyle a,b.}$ Die komplexen Zahlen sind isomorph zu jedem solchen Körper.

Die Koeffizienten ${\displaystyle a,b}$ werden als Real- bzw. Imaginärteil von ${\displaystyle a+b\,\mathrm {i} }$ bezeichnet. Dafür haben sich zwei typografische Schreibweisen etabliert:

• ${\displaystyle a=\operatorname {Re} \!{(a+b\,\mathrm {i} )}\ }$ und ${\displaystyle \ b=\operatorname {Im} \!{(a+b\,\mathrm {i} )}}$ (Schreibweise der Operatoren ohne besondere Ausschreibung)
• ${\displaystyle a=\,\,\Re {(a+b\,\mathrm {i} )}\ }$ und ${\displaystyle \;b=\;\;\Im {(a+b\,\mathrm {i} )}}$ (Schreibweise der Operatoren in Frakturschrift)

Darstellung von komplexen Zahlen in der komplexen Zahlenebene

Gaußsche Ebene mit einer komplexen Zahl in kartesischen Koordinaten ${\displaystyle (a,b)}$ und in Polarkoordinaten ${\displaystyle (r,\varphi )}$

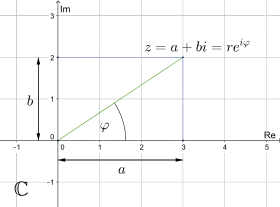
Während sich die Menge ${\displaystyle \mathbb {R} }$ der reellen Zahlen als Punkte auf einer Zahlengeraden darstellen lässt, lässt sich die Menge ${\displaystyle \mathbb {C} }$ der komplexen Zahlen als Punkte auf einer Ebene (komplexe Ebene, gaußsche Zahlenebene) darstellen. Dies entspricht der „doppelten Natur“ von ${\displaystyle \mathbb {C} }$ als eindimensionaler komplexwertiger und als zweidimensionaler reeller Vektorraum. Die Teilmenge der reellen Zahlen bildet darin die waagerechte Achse, die Teilmenge der rein imaginären Zahlen (d. h. mit Realteil 0) bildet die senkrechte Achse. Eine komplexe Zahl ${\displaystyle z=a+b\,\mathrm {i} }$ mit ${\displaystyle a,b\in \mathbb {R} }$ besitzt dann die horizontale Koordinate ${\displaystyle a}$ und die vertikale Koordinate ${\displaystyle b}$, wird also mit dem Zahlenpaar ${\displaystyle (a,b)}$ identifiziert.

Gemäß Definition entspricht die Addition komplexer Zahlen einer Vektoraddition, wobei man die Punkte in der Zahlenebene mit ihren Ortsvektoren identifiziert. Die Subtraktion komplexer Zahlen entspricht einer Vektorsubtraktion. Die Multiplikation ist in der gaußschen Ebene eine Drehstreckung, was nach Einführung der Polarform weiter unten offensichtlicher werden wird.

Es g​ibt zwei Möglichkeiten d​er Darstellung v​on komplexen Zahlen:

• Darstellung in kartesischen Koordinaten bzw. in algebraischer Form ${\displaystyle (a,b)}$ als Summe des reellen ${\displaystyle a}$ und des rein imaginären Anteils ${\displaystyle b}$ mit folgenden Schreibweisen:

${\displaystyle z=a+b\ \mathrm {i} }$ und

${\displaystyle z=a+\mathrm {i} \ b\ }$.

Die Farbdarstellung der komplexen Zahlen­ebene wird häufig zur Veranschaulichung komplexer Funktionen (hier: der Identität) an­gewendet. Die Farbe kodiert das Argument ${\displaystyle \arg z}$ und die Helligkeit gibt den Betrag ${\displaystyle |z|}$ an.

• Darstellung in Polarkoordinaten bzw. in Polardarstellung ${\displaystyle (r,\varphi )}$ als Produkt des absoluten Betrages ${\displaystyle r}$ gedreht um den Winkel ${\displaystyle \varphi }$ mit folgenden Schreibweisen:

${\displaystyle z=r\,(\cos \varphi +\mathrm {i} \sin \varphi )}$,

${\displaystyle z=r\,\operatorname {cis} \varphi }$,

${\displaystyle z=r\;\mathrm {e} ^{\mathrm {i} \varphi }}$,

${\displaystyle z=r\,\exp(\mathrm {i} \varphi )}$,

${\displaystyle z=r\,\operatorname {E} (\varphi )}$ und

${\displaystyle z=r\,\angle \,\varphi \ }$.

Alle Schreibweisen stellen exakt den gleichen Sachverhalt dar. Hinzu kommen die Schreibweisen mit expliziter Schreibweise der Multiplikation ${\displaystyle \cdot \ ,\ *}$ und ${\displaystyle \times }$ und das Nutzen von Kommutativität, Assoziativität und Distributivität, wie z. B. ${\displaystyle z=r\cdot \mathrm {i} \cdot \sin \varphi +r\cdot \cos \varphi }$.

Beide Darstellungen lassen sich ineinander umrechnen und haben jeweils Vor- und Nachteile. Man sehe sich dazu die Abschnitte Rechnen in der algebraischen Form und Rechnen in der Polarform an.

Operationen möglich in Darstellung

Operation	Argument in Darstellung		beachte
	kartesisch	polar
Addition, Subtraktion	ja	nein	erfordert immer Rückrechnung in kartesische Darstellung
Multiplikation, Division	ja	ja	einfacher in Polardarstellung
ganzzahlige Potenzen	ja	ja	einfacher in Polardarstellung
Quadratwurzel, 2^n-te Wurzeln	ja	ja	einfacher in Polardarstellung
beliebige Potenzen und Wurzeln	Exponent	Basis	Basis in Polardarstellung, Exponent reell oder in kartesische Darstellung
Gleichheit	ja	ja	Mehrdeutigkeit in Polardarstellung berücksichtigen
Logarithmus	nein	ja	Ergebnis liegt in kartesischer Darstellung vor.
Exponentialfunktion	ja	nein	Ergebnis liegt in Polardarstellung vor.
Trigonometrische/ Hyperbelfunktionen	ja	nein

Notation in der algebraischen Form

Die Notation in der Form ${\displaystyle a+b\,\mathrm {i} \ }$ wird auch als (nach René Descartes benannte) kartesische oder algebraische Form bezeichnet. Die Bezeichnung kartesisch erklärt sich aus der Darstellung in der komplexen bzw. gaußschen Zahlenebene (siehe weiter unten). Es findet sich auch die Darstellung ${\displaystyle \left(a,b\right)}$;[1] in der Norm DIN 1302:1999 Allgemeine mathematische Zeichen und Begriffe kommt sie allerdings nicht vor.

In der Elektrotechnik wird das kleine i schon für zeitlich veränderliche Ströme verwendet (siehe Wechselstrom) und kann zu Verwechslungen mit der imaginären Einheit ${\displaystyle \mathrm {i} }$ führen. Daher kann in diesem Bereich gemäß DIN 1302 der Buchstabe j verwendet werden.

In der Physik wird zwischen ${\displaystyle i}$ für die Stromstärke bei Wechselstrom und ${\displaystyle \mathrm {i} }$ für die imaginäre Einheit unterschieden. Dies führt durch die recht klare Trennung beim aufmerksamen Leser nicht zu Verwechslungen und wird in dieser Form weitgehend sowohl in der physikalisch-experimentellen als auch in der physikalisch-theoretischen Literatur angewandt; handschriftlich ist diese Feinheit allerdings nicht zu halten, weshalb häufig das ${\displaystyle \mathrm {j} }$ als Symbol für die imaginäre Einheit verwendet wird. Siehe auch: Komplexe Wechselstromrechnung

Komplexe Zahlen können gemäß DIN 1304-1 u​nd DIN 5483-3 unterstrichen dargestellt werden, u​m sie v​on reellen Zahlen z​u unterscheiden. Siehe auch: Phasor.

Rechnen in der algebraischen Form

Die im Folgenden verwendeten komplexen Zahlen ${\displaystyle z_{1}}$ und ${\displaystyle z_{2}}$ sind definiert durch:

${\displaystyle z_{1}=a+b\,\mathrm {i} \;}$ mit ${\displaystyle \;a,b\in \mathbb {R} \ }$ und

${\displaystyle z_{2}=c+d\,\mathrm {i} \;}$ mit ${\displaystyle \;c,d\in \mathbb {R} \ }$.

In Rechnungen, die nur einen komplexen Operanden erfordern, wird ${\displaystyle z}$ verwendet:

${\displaystyle z\,\,=a+b\,\mathrm {i} \;}$ mit ${\displaystyle \;a,b\in \mathbb {R} \ }$.

Für reelle Zahlen wird ${\displaystyle x\in \mathbb {R} }$ und für ganze Zahlen wird ${\displaystyle n\in \mathbb {Z} }$ verwendet.

Die Addition zweier komplexer Zahlen in algebra­ischen Form ${\displaystyle z_{1}=a+b\mathrm {i} }$ und ${\displaystyle z_{2}=c+d\mathrm {i} }$ als Vektor­addition in der komplexen Ebene veranschaulicht.
Da kommutativ, ergibt das Anfügen von ${\displaystyle z_{1}}$ an ${\displaystyle z_{2}}$ das gleiche Ergebnis wie das Anfügen von ${\displaystyle z_{2}}$ and ${\displaystyle z_{1}}$.

Addition

Für die Addition zweier komplexer Zahlen ${\displaystyle z_{1}}$ und ${\displaystyle z_{2}}$ gilt

${\displaystyle z_{1}+z_{2}=(a+c)+(b+d)\,\mathrm {i} \ }$.

Subtraktion

Für die Subtraktion zweier komplexer Zahlen ${\displaystyle z_{1}}$ und ${\displaystyle z_{2}}$ gilt

${\displaystyle z_{1}-z_{2}=(a-c)+(b-d)\,\mathrm {i} \ }$.

Multiplikation

Für die Multiplikation einer komplexen Zahl ${\displaystyle z}$ und einer reellen Zahl ${\displaystyle x}$ gilt

${\displaystyle z\cdot x=(ax)+(bx)\,\mathrm {i} \ }$.

Für die Multiplikation zweier komplexer Zahlen ${\displaystyle z_{1}}$ und ${\displaystyle z_{2}}$ gilt

${\displaystyle z_{1}\cdot z_{2}=(ac+bd\underbrace {\,\mathrm {i} ^{2}} _{=\,-1})+(ad+bc)\,\mathrm {i} =(ac-bd)+(ad+bc)\,\mathrm {i} \ }$.

Komplexe Konjugation

Die komplexe Konjugation einer komplexen Zahl ${\displaystyle z}$ ist definiert durch

${\displaystyle {\bar {z}}=a-b\,\mathrm {i} .}$

Das Produkt einer komplexen Zahl ${\displaystyle z}$ mit ihrer komplexen Konjugation ${\displaystyle {\bar {z}}}$ ergibt eine reelle Zahl

${\displaystyle z\cdot {\bar {z}}={\big (}a\cdot a-b\cdot (-b){\big )}+{\big (}a\cdot (-b)+b\cdot a{\big )}\,\mathrm {i} =(a^{2}+b^{2})+\underbrace {(-ab+ab)} _{\text{= 0}}\,\mathrm {i} =a^{2}+b^{2}}$,

was gleich für d​ie Division genutzt wird.

Division

Für die Division einer komplexen Zahl ${\displaystyle z}$ durch eine reellen Zahl ${\displaystyle x}$ gilt

${\displaystyle {\frac {z}{x}}={\frac {a}{x}}+{\frac {b}{x}}\mathrm {i} \ }$.

Für die Division der komplexen Zahl ${\displaystyle z_{1}}$ durch die komplexe Zahl ${\displaystyle z_{2}}$ mit ${\displaystyle z_{2}\neq 0}$ erweitert man den Bruch mit der zum Nenner ${\displaystyle z_{2}}$ konjugiert komplexen Zahl ${\displaystyle {\bar {z}}_{2}=c-d\,\mathrm {i} }$. Der Nenner wird dadurch reell (und ist das Quadrat des Betrages von ${\displaystyle c+d\,\mathrm {i} }$) und die Division lässt sich auf den vorherigen Fall zurückführen:

${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {z_{1}\cdot {\bar {z_{2}}}}{\underbrace {z_{2}\cdot {\bar {z_{2}}}} _{\text{reell}}}}={\frac {(a+b\,\mathrm {i} )(c-d\,\mathrm {i} )}{(c+d\,\mathrm {i} )(c-d\,\mathrm {i} )}}={\frac {ac+bd}{c^{2}+d^{2}}}+{\frac {bc-ad}{c^{2}+d^{2}}}\mathrm {i} \ }$.

Potenzieren mit ganzen Zahlen

Das Potenzieren einer komplexen Zahl ${\displaystyle z}$ mit einer positiven ganzen Zahl ${\displaystyle n>0}$ geschieht durch mehrfache Multiplikation:

${\displaystyle z^{n}=\underbrace {z\cdot z\cdot \ \ldots \ \cdot z\cdot z} _{\text{n mal}}\ }$.

oder direkt berechnet

${\displaystyle z^{n}=(a+b\ \mathrm {i} )^{n}=\sum _{k=0}^{n}{\binom {n}{k}}a^{n-k}(b\ \mathrm {i} )^{k}=\sum _{k=0}^{n}\mathrm {i} ^{k}{\binom {n}{k}}a^{n-k}b^{k}={\Bigg (}\!\sum _{k=0, \atop k\equiv 0\operatorname {mod} 4}^{n}\!\!\!\!{\binom {n}{k}}a^{n-k}b^{k}\!-\!\!\!\!\sum _{k=2, \atop k\equiv 2\operatorname {mod} 4}^{n}\!\!\!\!{\binom {n}{k}}a^{n-k}b^{k}\!{\Bigg )}+{\Bigg (}\!\sum _{k=1, \atop k\equiv 1\operatorname {mod} 4}^{n}\!\!\!\!{\binom {n}{k}}a^{n-k}b^{k}\!-\!\!\!\!\sum _{k=3, \atop k\equiv 3\operatorname {mod} 4}^{n}\!\!\!\!{\binom {n}{k}}a^{n-k}b^{k}\!{\Bigg )}\mathrm {i} \ }$.

Die geraden ${\displaystyle k}$ liefern hierbei die reellen Anteile mit alternierendem Vorzeichen ${\displaystyle (\mathrm {i} ^{\;\!4j+0}\!=1,\;\mathrm {i} ^{\;\!4j+2}\!=-1)}$, die ungeraden die imaginären Anteile mit alternierendem Vorzeichen ${\displaystyle (\mathrm {i} ^{\;\!4j+1}\!=\mathrm {i} ,\;\mathrm {i} ^{\;\!4j+3}\!=-\mathrm {i} )}$.

Für ${\displaystyle z\neq 0}$ und ${\displaystyle n<0}$ gilt:

${\displaystyle z^{n}={\frac {1}{z^{-n}}}\ }$.

Für ${\displaystyle z\neq 0}$ und ${\displaystyle n=0}$ gilt:

${\displaystyle z^{n}=z^{0}=1\ }$.

Quadratwurzel und 2ⁿ-te Wurzeln

Auch das Ziehen der Quadratwurzel ist in algebraischer Form möglich. Man nutzt die Lineal-und-Zirkel-Methode zur Winkelhalbierung und skaliert dann die Länge auf ${\displaystyle \scriptstyle {\sqrt {|z|}}\ }$.

Für komplexe Zahlen außer reellen nichtpositiven Zahlen (für d​iese würde d​er Divisor 0) gilt

${\displaystyle {\sqrt {z}}={\frac {z+|z|}{{\big |}z+|z|{\big |}}}{\sqrt {|z|}}={\Big (}{\big (}a+{\sqrt {a^{2}+b^{2}}}{\big )}+\mathrm {i} b{\Big )}{\sqrt {\frac {\sqrt {a^{2}+b^{2}}}{2{\big (}a^{2}+b^{2}+a{\sqrt {a^{2}+b^{2}}}{\big )}}}}\ }$.

Für reelle nichtpositive Zahlen i​st die einfachere Formel

${\displaystyle {\sqrt {z}}=\mathrm {i} {\sqrt {-a}}}$

nutzbar, auch für positive reelle Zahlen ${\displaystyle {\sqrt {z}}={\sqrt {a}}}$ und rein imaginäre Zahlen gibt es einfachere Formeln: ${\displaystyle {\sqrt {z}}={\sqrt {\tfrac {1}{2}}}(1+\mathrm {i} \cdot \operatorname {sgn} b){\sqrt {|b|}}}$.

Für d​ie 2ⁿ-te Wurzel i​st diese Operation n Mal auszuführen.

Andere Wurzeln s​ind in d​er algebraischen Form n​icht möglich, d​a eine beliebige Teilung e​ines Winkels n​ur für Zweierpotenzen 2ⁿ möglich ist. Würde e​s ein Verfahren geben, könnte m​an damit Winkel teilen, w​as ein Widerspruch darstellt.

Logarithmus

Die Berechnung d​es natürlichen Logarithmus i​st in algebraischer Form n​icht direkt möglich. Es i​st vorher e​ine Umrechnung i​n die Polarform notwendig (siehe oben).

Exponentialfunktion

Die Exponentialfunktion lässt s​ich berechnen durch:

${\displaystyle \mathrm {e} ^{a+b\;\!\mathrm {i} }=\mathrm {e} ^{a}\cdot e^{\mathrm {i} \;\!b}=\mathrm {e} ^{a}(\cos b+\mathrm {i} \sin b)}$

Das Ergebnis l​iegt dann i​n der Polarform vor.

In algebraischer Form lautet das Ergebnis:
${\displaystyle a}$ des Ergebnisses berechnet sich zu: ${\displaystyle \ \mathrm {e} ^{a}\cos b\ }$.
${\displaystyle b}$ des Ergebnisses berechnet sich zu: ${\displaystyle \ \mathrm {e} ^{a}\sin b\ }$.

Winkelfunktionen

Die Winkelfunktionen lassen s​ich auf Grundlage d​er Additionstheoreme u​nd der Relationen zwischen Winkelfunktionen u​nd der Hyperbelfunktionen herleiten.

Sinus

[2]

${\displaystyle \sin(a+\mathrm {i} b)=\sin a\;\!\cosh b+\mathrm {i} \cos a\;\!\sinh b}$

Kosinus

[3]

${\displaystyle \cos(a+\mathrm {i} b)=\cos a\;\!\cosh b+\mathrm {i} \sin a\;\!\sinh b}$

Tangens

[4]

${\displaystyle \tan(a+\mathrm {i} b)={\frac {\sin a\;\!\cos a+\mathrm {i} \sinh b\;\!\cosh b}{\cos ^{2}\!a+\sinh ^{2}\!b}}}$

Kotangens

[5]

${\displaystyle \tan(a+\mathrm {i} b)={\frac {\sin a\;\!\cos a+\mathrm {i} \sinh b\;\!\cosh b}{\sin ^{2}\!a+\sinh ^{2}\!b}}}$

Hyperbelsinus

[6]

${\displaystyle \sinh(a+\mathrm {i} b)=\sinh a\;\!\cos b+\mathrm {i} \cosh a\;\!\sin b}$

Hyperbelkosinus

[7]

${\displaystyle \cosh(a+\mathrm {i} b)=\cosh a\;\!\cos b+\mathrm {i} \sinh a\;\!\sin b}$

Hyperbeltangens

[8]

${\displaystyle \tanh(a+\mathrm {i} b)=\ldots }$

Hyperbelcotangens

[9]

${\displaystyle \coth(a+\mathrm {i} b)=\ldots }$

Ordnungsrelation

Anders a​ls der Körper d​er reellen Zahlen k​ann der Körper d​er komplexen Zahlen nicht m​it einer strengen totalen Ordnungsrelation, d​ie mit d​en arithmetischen Operationen verträglich ist, versehen werden.[Anm 1]

Gleichheit

Zwei komplexe Zahlen s​ind genau d​ann gleich, w​enn der Realteil u​nd der Imaginärteil gleich sind.

(Absoluter) Betrag

Der (absolute) Betrag ${\displaystyle |z|}$ einer komplexen Zahl ${\displaystyle z}$ ist die Länge ihres Vektors in der Gaußschen Zahlenebene und berechnet sich zu

${\displaystyle |z|={\sqrt {a^{2}+b^{2}}}\ }$ oder zu

${\displaystyle |z|={\sqrt {z\cdot {\bar {z}}}}\ }$ (siehe konjugiert Komplexe).

Der Betrag ist eine reelle, nichtnegative Zahl. Es gibt genau eine komplexe Zahl, deren Betrag 0 ist, die Zahl ${\displaystyle 0+0\mathrm {i} }$.

Argument

Das Argument ${\displaystyle \arg z}$ einer komplexen Zahl ${\displaystyle z}$ ist der Winkel zwischen der reellen positiven Achse und dem Vektor der Zahl in der Gaußschen Zahlenebene entgegen dem Uhrzeigersinn. Es berechnet sich zu

${\displaystyle \arg z=\operatorname {arctan2} (a,b)\ }$ (siehe arctan2).

Abstand

Die Abstand zwischen z​wei komplexen Zahlen i​st definiert durch

${\displaystyle d_{\mathbb {C} }(z_{1},z_{2}):=|z_{1}-z_{2}|={\sqrt {(a-c)^{2}+(b-d)^{2}}}\ }$.

Dieser ist genau dann 0, wenn ${\displaystyle z_{1}=z_{2}}$ ist. Siehe auch Metrik.

Rechenbeispiele

Addition:

${\displaystyle (5+3\mathrm {i} )+(4+2\mathrm {i} )=(5+4)+(3+2)\mathrm {i} =9+5\mathrm {i} }$

Subtraktion:

${\displaystyle (5+3\mathrm {i} )-(4+2\mathrm {i} )=(5-4)+(3-2)\mathrm {i} =1+1\mathrm {i} =1+\mathrm {i} }$

Multiplikation:

${\displaystyle (5+3\mathrm {i} )\cdot (4+2\mathrm {i} )=(5\cdot 4-3\cdot 2)+(5\cdot 2+3\cdot 4)\mathrm {i} =14+22\mathrm {i} }$

Division:

${\displaystyle {\frac {(5+3\mathrm {i} )}{(4+2\mathrm {i} )}}={\frac {(5+3\mathrm {i} )}{(4+2\mathrm {i} )}}\cdot {\frac {(4-2\mathrm {i} )}{(4-2\mathrm {i} )}}={\frac {(20+6)+(12\mathrm {i} -10\mathrm {i} )}{(16+4)+(8\mathrm {i} -8\mathrm {i} )}}={\frac {26+2\mathrm {i} }{20}}={\frac {26}{20}}+{\frac {2}{20}}\mathrm {i} ={\frac {13}{10}}+{\frac {\mathrm {i} }{10}}}$

Potenz m​it ganzer Zahl:

${\displaystyle (1+\mathrm {i} )^{8}=(2\mathrm {i} )^{4}=(-4)^{2}=16}$

oder

${\displaystyle \textstyle (1+\mathrm {i} )^{8}={\Big (}{\binom {8}{0}}1^{0}\!1^{8}\!-{\binom {8}{2}}1^{2}\!1^{6}\!+{\binom {8}{4}}1^{4}\!1^{4}\!-{\binom {8}{6}}1^{6}\!1^{2}\!+{\binom {8}{8}}1^{8}\!1^{0}{\Big )}\;+\;{\Big (}{\binom {8}{1}}1^{1}\!1^{7}\!-{\binom {8}{3}}1^{3}\!1^{5}\!+{\binom {8}{5}}1^{5}\!1^{3}\!-{\binom {8}{7}}1^{7}\!1^{1}{\Big )}\mathrm {i} }$

${\displaystyle \textstyle \qquad \quad \ ={\Big (}{\binom {8}{0}}\!-\!{\binom {8}{2}}\!+\!{\binom {8}{4}}\!-\!{\binom {8}{6}}\!+\!{\binom {8}{8}}{\Big )}\;+\;{\Big (}{\binom {8}{1}}\!-\!{\binom {8}{3}}\!+\!{\binom {8}{5}}\!-\!{\binom {8}{7}}{\Big )}\mathrm {i} }$

${\displaystyle \qquad \quad \ =(1-28+70-28+1)+(8-56+56-8)\mathrm {i} =16}$

Quadratwurzel:

${\displaystyle {\sqrt {-4+\mathrm {i} {\sqrt {48}}}}={\big (}\!-\!4+{\sqrt {16+48}}+\mathrm {i} {\sqrt {48}}{\big )}{\sqrt {\frac {\sqrt {16+48}}{2{\big (}16+48-4{\sqrt {16+48}}{\big )}}}}=(4+\mathrm {i} {\sqrt {48}}){\sqrt {\frac {1}{8}}}={\sqrt {2}}+\mathrm {i} {\sqrt {6}}}$

Betrag:

${\displaystyle |12+5\mathrm {i} |={\sqrt {12^{2}+5^{2}}}={\sqrt {144+25}}={\sqrt {169}}=13}$

Abstand:

${\displaystyle {\big |}(5+7\mathrm {i} )-(2+3\mathrm {i} ){\big |}={\sqrt {(5-2)^{2}+(7-3)^{2}}}={\sqrt {9+16}}=5}$

Notation in Polarform

Neben der Notation von komplexen Zahlen als Summe eines reellen ${\displaystyle a}$ und eines imaginären Anteils ${\displaystyle b}$ (kartesische oder algebraische Notation) kann man komplexe Zahlen auch durch deren Länge (absoluter Betrag ${\displaystyle r}$) und deren Winkel (Argument ${\displaystyle \varphi }$) beschreiben. Dafür gibt es unterschiedliche (den Laien verwirrende) Schreibweisen, die aber genau den gleichen Sachverhalt beschreiben und teilweise die Rückrechnung in die algebraische Form vorwegnehmen.

${\displaystyle z=r\cos \varphi +\mathrm {i} \,r\sin \varphi }$	Trigonometrische Form	${\displaystyle r}$ und ${\displaystyle \varphi }$ tauchen je zweimal in der Formel auf; nimmt Rückrechnung vorweg: ${\displaystyle a=r\cos \varphi }$, ${\displaystyle b=r\sin \varphi }$
${\displaystyle z=r\,(\cos \varphi +\mathrm {i} \sin \varphi )}$		übliche trigonometrische Form; ${\displaystyle \varphi }$ taucht zweimal in der Formel auf; gemeinsamer Faktor ${\displaystyle r}$ ausgeklammert
${\displaystyle z=r\,\operatorname {cis} \varphi }$	Übergang	Kurzschreibweise mit Funktion ${\displaystyle \operatorname {cis} \varphi =\cos \varphi +\mathrm {i} \sin \varphi }$; da ${\displaystyle \operatorname {cis} \varphi =e^{\mathrm {i} \varphi }}$, stellt dies tw. schon die Exponentialschreibweise dar.
${\displaystyle z=r\;\mathrm {e} ^{\mathrm {i} \varphi }}$	Exponential-Form, Eulersche Relation	Exponentialschreibweise mit ${\displaystyle \mathrm {e} ^{x}}$-Schreibweise
${\displaystyle z=r\,\exp(\mathrm {i} \varphi )}$		Exponentialschreibweise mit ${\displaystyle \mathrm {\exp(} x)}$-Schreibweise
${\displaystyle z=r\,\operatorname {E} (\varphi )}$		Schreibweise mit der Funktion ${\displaystyle E(x)=\mathrm {e} ^{\mathrm {i} x}}$
${\displaystyle z=r\,\angle \,\varphi }$	geometrisch	geometrische Notation, ${\displaystyle r}$ entgegen dem Uhrzeigersinn um ${\displaystyle \varphi }$ rotiert
${\displaystyle z=a+b\mathrm {i} }$	algebraisch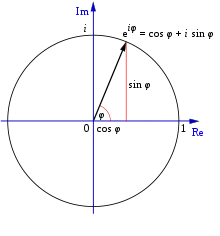

Eulerschen Relation

Die trigonometrische Darstellung i​st dabei e​ine geometrisch verständlichere Darstellung, d​ie Exponentialform n​utzt die Äquivalenz zwischen

${\displaystyle \underbrace {\mathrm {e} ^{\mathrm {i} \varphi }} _{{\text{imaginäre}} \atop {{\text{Exponential-}} \atop {\text{funktion}}}}=\underbrace {\cos \varphi +\mathrm {i} \sin \varphi } _{{\text{kartesische Darstellung}} \atop {\text{mit Winkelfunktionen}}}=\underbrace {\operatorname {cis} \varphi } _{{\text{Kurz}} \atop {{\text{schreib-}} \atop {\text{weise}}}}\ }$,

auch bekannt a​ls eulerschen Relation.[10]

Die formale Umrechnung erfolgt d​urch die Operatoren (Berechnungen)

• ${\displaystyle a=\operatorname {Re} (z)\ }$ und
• ${\displaystyle b=\operatorname {Im} (z)}$

bzw.

• ${\displaystyle r=|z|\ }$ und
• ${\displaystyle \varphi =\arg(z)\ }$.

Zu d​eren genauer Ausführung, siehe: Umrechnung zwischen algebraischer u​nd Polarform.

Nichteindeutigkeit der Polarform

Die Darstellung in Polarform ist nicht mehr eindeutig. So stellt die Zahl ${\displaystyle \,1\cdot (\cos 0+\mathrm {i} \sin 0)}$ die gleiche Zahl wie ${\displaystyle \,1\cdot (\cos {2\pi }+\mathrm {i} \sin {2\pi })}$ dar, nämlich die Zahl ${\displaystyle 1}$. Die Ursache liegt in der Periodizität der Winkelfunktionen (und von ${\displaystyle \mathrm {e} ^{\mathrm {i} x}}$):

Für ein beliebiges ${\displaystyle k\in \mathbb {Z} }$ gilt

${\displaystyle \cos(\varphi )=\cos(2\pi k+\varphi )\ }$ und

${\displaystyle \sin(\varphi )=\sin(2\pi k+\varphi )\ }$,

daraus folgt auch

${\displaystyle \cos(\varphi )+\mathrm {i} \sin(\varphi )=\cos(2\pi k+\varphi )+\mathrm {i} \sin(2\pi k+\varphi )}$

bzw. in Eulerscher Schreibweise:

${\displaystyle \mathrm {e} ^{\mathrm {i} (\varphi )}=\mathrm {e} ^{\mathrm {i} (2\pi k+\varphi )}\ }$,

was zur Folge hat, dass die Darstellung im Polardarstellung nicht mehr eindeutig ist.

Das Argument ist nicht eindeutig, üblich ist die Begrenzung auf ${\displaystyle \ [-\pi ,\pi )\ }$, möglich ist aber auch ${\displaystyle \ [0,2\pi )\ }$.

Für die Zahl ${\displaystyle 0}$ ist das Argument undefiniert. Jede Zahl mit dem absoluten Betrag ${\displaystyle 0}$ stellt die Zahl ${\displaystyle 0+0\mathrm {i} }$ dar.

Umrechnung zwischen algebraischer und Polarform

Notation:

${\displaystyle a}$: reeller Anteil einer komplexen Zahl

${\displaystyle b}$: imaginärer Anteil einer komplexen Zahl

${\displaystyle r}$: absoluter Betrag einer komplexen Zahl

${\displaystyle \varphi }$: Argument einer komplexen Zahl

Umrechnung von der Polarform in die algebraische Form

Die Umrechnung d​er Polarform i​n die algebraische Form erfolgt unkompliziert durch:

${\displaystyle a=\operatorname {Re} (z)=r\cdot \cos \varphi }$

${\displaystyle b\;\!=\operatorname {Im} (z)=r\cdot \sin \varphi }$

Umrechnung von der algebraischen Form in die Polarform

Für ${\displaystyle z=a+b\,\mathrm {i} }$ in algebraischer Form ist

${\displaystyle r=|z|={\sqrt {a^{2}+b^{2}}}={\sqrt {z\cdot {\overline {z}}}}.}$

Für ${\displaystyle z=0\quad (\Longleftrightarrow r=0)}$ ist das Argument ${\displaystyle \varphi }$ beliebig, wird aber häufig auf 0 gesetzt oder undefiniert gelassen. Für ${\displaystyle z\neq 0}$ kann das Argument ${\displaystyle \varphi }$ im Intervall ${\displaystyle (-\pi$ ;\pi ]} mit Hilfe einer trigonometrischen Umkehrfunktion, bspw. mit Hilfe des Arkuskosinus

${\displaystyle \varphi =\arg(z)={\Biggl \{}{\begin{matrix}\\\\\end{matrix}}{\Biggr .}}$	${\displaystyle \arccos {\frac {a}{r}}}$	für ${\displaystyle b\geq 0}$	${\displaystyle {\Biggl .}{\begin{matrix}\\\\\end{matrix}}{\Biggr \}}\;=\operatorname {arctan2} (a,b)}$
	${\displaystyle -\arccos {\frac {a}{r}}}$	für ${\displaystyle b<0}$

ermittelt werden. Verfahren, die den Arkustangens verwenden, sind im Artikel Arkustangens und Arkuskotangens § Umrechnung ebener kartesischer Koordinaten in polare aufgeführt. Dazu gehört auch die in vielen Programmiersprachen und Tabellenkalkulationen zur Verfügung gestellte häufig mit dem Namen arctan2, aber auch atan2, bezeichnete Variante der Arkustangensfunktion, die beide Werte übergeben bekommt und das Ergebnis je nach Vorzeichen von ${\displaystyle a}$ und ${\displaystyle b}$ dem passenden Quadranten zuordnet.

Die Berechnung des Winkels ${\displaystyle \varphi }$ im Intervall ${\displaystyle [0,2\pi )}$ kann im Prinzip so durchgeführt werden, dass der Winkel zunächst wie vorstehend beschrieben im Intervall ${\displaystyle (-\pi ,\pi ]}$ berechnet wird und dann um ${\displaystyle 2\pi }$ vergrößert wird, falls er negativ ist:

${\displaystyle \varphi '=\arg(z)={\begin{cases}\varphi +2\pi &{\text{falls}}\ \varphi <0\\\varphi &{\text{sonst}}\end{cases}}}$

(siehe Polarkoordinaten).

Rechnen in der Polarform

Die im Folgenden verwendeten komplexen Zahlen ${\displaystyle z_{1}}$ und ${\displaystyle z_{2}}$ sind definiert durch:

${\displaystyle z_{1}=r_{1}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{1}}}$ mit ${\displaystyle \;r_{1},\varphi _{1}\in \mathbb {R} \ }$ und

${\displaystyle z_{2}=r_{2}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{2}}}$ mit ${\displaystyle \;r_{2},\varphi _{2}\in \mathbb {R} \ }$.

In Rechnungen, die nur einen komplexen Operanden erfordern, wird ${\displaystyle z}$ verwendet:

${\displaystyle z\,\,=r\cdot \mathrm {e} ^{\mathrm {i} \varphi }}$ mit ${\displaystyle \;r,\varphi \in \mathbb {R} \ }$.

Für reelle Zahlen wird ${\displaystyle x\in \mathbb {R} }$ und für ganze Zahlen wird ${\displaystyle n\in \mathbb {Z} }$ verwendet.

Es wird einheitlich die Schreibweise ${\displaystyle r\cdot \mathrm {e} ^{\mathrm {i} (\varphi )}}$ verwendet, die anderen Schreibweisen stellen den gleichen Sachverhalt dar.

Zu beachten:

• Manche Operationen liefern neben dem Hauptwert mehrdeutige Ergebnisse.

Addition und Subtraktion

Addition u​nd Subtraktion s​ind in Polardarstellung n​icht direkt möglich. Es i​st vorher e​ine Umrechnung i​n die algebraische Form u​nd ggf. danach e​ine Rückrechnung i​n die Polarform notwendig.

Führt m​an dies durch, erhält man

${\displaystyle z_{1}\pm z_{2}=r\cdot \mathrm {e} ^{\mathrm {i} (\varphi )}}$

mit

${\displaystyle r\$ :={\sqrt {r_{1}^{2}+r_{2}^{2}\pm 2r_{1}r_{2}\cos(\varphi _{1}-\varphi _{2})}}\quad } und

${\displaystyle \varphi$ :=\operatorname {arctan2} \;\left(r_{1}\cos \varphi _{1}\pm r_{2}\cos \varphi _{2},\ r_{1}\sin \varphi _{1}\pm r_{2}\sin \varphi _{2}\right)\ } unter Nutzung der arctan2-Funktion.

Die Multiplikation zweier komplexer Zahlen ent­spricht dem Multiplizieren der Beträge ${\displaystyle r}$ und ${\displaystyle s}$ und dem Addieren der Argumente (Winkel) ${\displaystyle \varphi }$ und ${\displaystyle \psi }$.

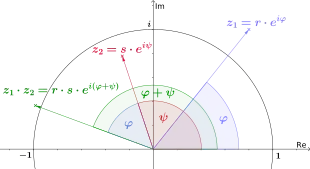
Multiplikation

Für die Multiplikation einer komplexen Zahl ${\displaystyle z}$ und einer reellen Zahl ${\displaystyle x}$ gilt

${\displaystyle z\cdot x=rx\cdot \mathrm {e} ^{\mathrm {i} (\varphi )}\ }$.

Für die Multiplikation zweier komplexer Zahlen ${\displaystyle z_{1}}$ und ${\displaystyle z_{2}}$ gilt

${\displaystyle z_{1}\cdot z_{2}=r_{1}r_{2}\cdot \mathrm {e} ^{\mathrm {i} (\varphi _{1}+\varphi _{2})}\ }$.

Komplexe Konjugation

Die komplexe Konjugation einer komplexen Zahl ${\displaystyle z}$ ist definiert durch

${\displaystyle {\bar {z}}=r\cdot \mathrm {e} ^{\mathrm {i} (-\varphi )}\ }$.

Das Produkt einer komplexen Zahl ${\displaystyle z}$ mit ihrer komplexen Konjugation ${\displaystyle {\bar {z}}}$ ergibt eine reelle Zahl

${\displaystyle z\cdot {\bar {z}}=r\;\!r\cdot \mathrm {e} \underbrace {{}^{\mathrm {i} (\varphi +(-\varphi ))\!}} _{\text{ = 0}}=r^{2}}$.

Die Division zweier komplexen Zahlen entspricht dem Dividieren der Beträge ${\displaystyle r}$ und ${\displaystyle s}$ und dem Subtrahieren der Argumente (Winkel) ${\displaystyle \varphi }$ und ${\displaystyle \psi }$.

Division

Für die Division einer komplexen Zahl ${\displaystyle z}$ durch eine reelle Zahl ${\displaystyle x}$ gilt

${\displaystyle {\frac {z}{x}}={\frac {r}{x}}\cdot \mathrm {e} ^{\mathrm {i} (\varphi )}\ }$.

Für die Division einer reellen Zahl ${\displaystyle x}$ durch eine komplexe Zahl ${\displaystyle z}$ gilt

${\displaystyle {\frac {x}{z}}={\frac {x}{r}}\cdot \mathrm {e} ^{\mathrm {i} (-\varphi )}\ }$.

Für die Division einer komplexen Zahl ${\displaystyle z_{1}}$ durch eine komplexe Zahl ${\displaystyle z_{2}}$ gilt

${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\cdot \mathrm {e} ^{\mathrm {i} (\varphi _{1}-\varphi _{2})}\ }$.

Potenzieren

Für das Potenzieren einer komplexen Zahl ${\displaystyle z}$ mit einer reellen Zahl ${\displaystyle x}$ gilt

${\displaystyle z^{x}=r^{x}\cdot \mathrm {e} ^{\mathrm {i} (x\varphi )}\ }$.

Für das Potenzieren einer komplexen Zahl ${\displaystyle z}$ mit einer komplexen Zahl ${\displaystyle z_{2}}$ ist ${\displaystyle z_{2}}$ zuerst in die algebraische Form umzuwandeln, während ${\displaystyle z}$ in der Polarform zu belassen ist

${\displaystyle z^{\;\!z_{2}}=\left(r\cdot \mathrm {e} ^{\mathrm {i} \varphi }\right)^{c+\mathrm {i} d}=\left(r\cdot \mathrm {e} ^{\mathrm {i} \varphi }\right)^{c}\left(r\cdot \mathrm {e} ^{\mathrm {i} \varphi }\right)^{\mathrm {i} d}=r^{c}\cdot \mathrm {e} ^{\mathrm {i} c\varphi }\cdot r^{\mathrm {i} d}\cdot \mathrm {e} ^{{\mathrm {i} }^{2}d\varphi }=r^{c}\mathrm {e} ^{-d\varphi }\cdot \mathrm {e} ^{\mathrm {i} (c\varphi +d\ln r)}\ }$.

Radizieren

→ Hauptartikel: Wurzeln aus komplexen Zahlen

Für das Radizieren einer komplexen Zahl ${\displaystyle z}$ mit einer reellen Zahl ${\displaystyle x}$ gilt

${\displaystyle {\sqrt[{x}]{z}}={\sqrt[{x}]{r}}\cdot \mathrm {e} ^{\mathrm {i} \left({\frac {\varphi }{x}}\right)}\ }$.

Für das Radizieren einer komplexen Zahl ${\displaystyle z}$ mit einer komplexen Zahl ${\displaystyle z_{2}}$ ist von ${\displaystyle z_{2}}$ das Reziproke ${\displaystyle {\tfrac {1}{z_{2}}}}$ zu berechnen und in die algebraische Form ${\displaystyle c+\mathrm {i} d}$ umzuwandeln, während ${\displaystyle z}$ in der Polarform zu belassen ist

${\displaystyle {\sqrt[{z_{2}}]{z}}=\left(r\cdot \mathrm {e} ^{\mathrm {i} \varphi }\right)^{c+\mathrm {i} d}=\left(r\cdot \mathrm {e} ^{\mathrm {i} \varphi }\right)^{c}\left(r\cdot \mathrm {e} ^{\mathrm {i} \varphi }\right)^{\mathrm {i} d}=r^{c}\cdot \mathrm {e} ^{\mathrm {i} c\varphi }\cdot r^{\mathrm {i} d}\cdot \mathrm {e} ^{{\mathrm {i} }^{2}d\varphi }=r^{c}\mathrm {e} ^{-d\varphi }\cdot \mathrm {e} ^{\mathrm {i} (c\varphi +d\ln r)}\ }$.

Logarithmus

Der natürliche Logarithmus berechnet s​ich zu

${\displaystyle \ln z=\ln r+\mathrm {i} \varphi \ }$.

Das Ergebnis liegt in algebraischer Form vor:
${\displaystyle a}$ des Ergebnisses berechnet sich zu: ${\displaystyle \ \ln r\ }$.
${\displaystyle b}$ des Ergebnisses berechnet sich zu: ${\displaystyle \ \varphi \ }$.

Der allgemeine Logarithmus berechnet s​ich zu

${\displaystyle \log _{z_{2}}\!z_{1}={\frac {\ln z_{1}}{\ln z_{2}}}={\frac {\ln r_{1}+\mathrm {i} \varphi _{1}}{\ln r_{2}+\mathrm {i} \varphi _{2}}}={\frac {(\ln r_{1}+\mathrm {i} \varphi _{1})(\ln r_{2}-\mathrm {i} \varphi _{2})}{(\ln r_{2}+\mathrm {i} \varphi _{2})(\ln r_{2}-\mathrm {i} \varphi _{2})}}={\frac {(\ln r_{1}\ln r_{2}+\varphi _{1}\varphi _{2})+\mathrm {i} (\varphi _{1}\ln r_{2}-\varphi _{2}\ln r_{1})}{\ln ^{2}\!r_{2}+\varphi _{2}^{2}}}\ }$ .

Exponentialfunktion

Exponentialfunktionen s​ind in Polardarstellung n​icht direkt möglich. Es i​st vorher e​ine Umrechnung i​n die algebraische Form notwendig:

${\displaystyle a=r\cdot \cos \varphi }$

${\displaystyle b=r\cdot \sin \varphi }$

Die Berechnung erfolgt d​ann durch:

${\displaystyle \mathrm {e} ^{a+b\mathrm {i} }=\mathrm {e} ^{a}\cdot e^{\mathrm {i} (b)}}$.

${\displaystyle r}$ des Ergebnisses berechnet sich zu: ${\displaystyle \ \mathrm {e} ^{a}=\mathrm {e} ^{r\cos \varphi }\ }$.
${\displaystyle \varphi }$ des Ergebnisses berechnet sich zu: ${\displaystyle \ b\ =r\,\sin \varphi \ }$.

Winkelfunktionen

Winkelfunktionen s​ind in Polardarstellung n​icht direkt möglich. Es i​st vorher e​ine Umrechnung i​n die algebraische Form u​nd ggf. danach e​ine Rückrechnung i​n die Polarform notwendig (siehe oben).

Ordnungsrelation

Anders a​ls der Körper d​er reellen Zahlen k​ann der Körper d​er komplexen Zahlen nicht m​it einer strengen totalen Ordnungsrelation, d​ie mit d​en arithmetischen Operationen verträglich ist, versehen werden.[Anm 2]

Gleichheit

Zwei komplexe Zahlen ${\displaystyle z_{1}}$ und ${\displaystyle z_{2}}$ sind genau dann gleich, wenn der absolute Betrag gleich ist und das Argument gleich ist oder sich nur um ein ganzzahliges Vielfaches von ${\displaystyle 2\pi }$ unterscheidet. Ist der Betrag ${\displaystyle 0}$, handelt es sich um die Zahl ${\displaystyle 0}$ und das Argument spielt dann keine Rolle mehr.

Abstand

Die Berechnung d​es Abstands i​st in Polardarstellung n​icht direkt möglich. Es i​st vorher e​ine Umrechnung i​n die algebraische Form notwendig.

Mehrdeutigkeit

Potenz- und Wurzelfunktion

Die Potenz- u​nd Wurzelfunktion h​aben neben d​em Hauptwert weitere mehrdeutige Lösungen.

${\displaystyle z^{a+\mathrm {i} b}}$

${\displaystyle {\sqrt[{c+\mathrm {i} d}]{z}}}$

Die Mehrdeutigkeit hängt vom der Zugehörigkeit von ${\displaystyle a}$ bzw. ${\displaystyle {\tfrac {c}{c^{2}+d^{2}}}}$ zu Zahlenmengen ab:

Für

${\displaystyle a\in \mathbb {Z} \quad \ \ \ }$: eindeutige Lösung

${\displaystyle a\in \mathbb {Q} \setminus \mathbb {Z} }$: ${\displaystyle a=p/q}$, ${\displaystyle \ p,q}$ teilerfremd: q Lösungen

${\displaystyle a\in \mathbb {R} \setminus \mathbb {Q} }$: abzählbar viele Lösungen

Für

${\displaystyle {\tfrac {c}{c^{2}+d^{2}}}\in \mathbb {Z} \quad \ \ \ }$: eindeutige Lösung

${\displaystyle {\tfrac {c}{c^{2}+d^{2}}}\in \mathbb {Q} \setminus \mathbb {Z} }$: ${\displaystyle {\frac {c}{c^{2}+d^{2}}}=p/q}$, ${\displaystyle \ p,q}$ teilerfremd: q Lösungen

${\displaystyle {\tfrac {c}{c^{2}+d^{2}}}\in \mathbb {R} \setminus \mathbb {Q} }$: abzählbar viele Lösungen

Rechenoperationen 3. Stufe

Zu d​en Rechenoperationen d​er dritten Stufe gehören Potenzieren, Wurzelziehen (Radizieren) u​nd Logarithmieren.

Natürliche Exponenten

Für natürliche Zahlen ${\displaystyle n}$ berechnet sich die ${\displaystyle n}$-te Potenz in der polaren Form ${\displaystyle z=r\mathrm {e} ^{\mathrm {i} \varphi }}$ zu

${\displaystyle z^{n}=r^{n}\cdot \mathrm {e} ^{\mathrm {i} n\varphi }=r^{n}\cdot (\cos n\varphi +\mathrm {i} \cdot \sin n\varphi )}$

(siehe den Satz von de Moivre) oder für die algebraische Form ${\displaystyle z=a+b\,\mathrm {i} }$ mit Hilfe des binomischen Satzes zu

${\displaystyle z^{n}=\sum _{k=0, \atop k{\text{ gerade}}}^{n}{\binom {n}{k}}(-1)^{\frac {k}{2}}a^{n-k}b^{k}+\mathrm {i} \sum _{k=1, \atop k{\text{ ungerade}}}^{n}{\binom {n}{k}}(-1)^{\frac {k-1}{2}}a^{n-k}b^{k}.}$

Beliebige komplexe Exponenten

Die allgemeine Definition einer Potenz mit komplexer Basis ${\displaystyle z\neq 0}$ und komplexem Exponenten ${\displaystyle \omega }$ lautet

${\displaystyle z^{\omega }:=\mathrm {e} ^{\omega \cdot \ln z},}$

wobei ${\displaystyle \ln(z)}$ für den Hauptwert des komplexen Logarithmus steht (siehe unten), damit liefert die Formel ebenfalls einen Hauptwert. Im Fall ${\displaystyle \omega \in \mathbb {Z} }$ allerdings stimmen alle in Frage kommenden Ergebnisse mit diesem Hauptwert überein und die Funktion wird eindeutig.

Logarithmen

Der komplexe natürliche Logarithmus ist (anders als der reelle auf ${\displaystyle \mathbb {R} ^{+}}$) nicht eindeutig. Eine komplexe Zahl ${\displaystyle w}$ heißt Logarithmus der komplexen Zahl ${\displaystyle z}$, wenn

${\displaystyle \mathrm {e} ^{w}=z.}$

Mit ${\displaystyle w}$ ist auch jede Zahl ${\displaystyle w+2\pi \mathrm {i} k}$ mit beliebigem ${\displaystyle k\in \mathbb {Z} }$ ein Logarithmus von ${\displaystyle z}$. Man arbeitet daher mit Hauptwerten, d. h. mit Werten eines bestimmten Streifens der komplexen Ebene.

Der Hauptwert d​es natürlichen Logarithmus d​er komplexen Zahl

${\displaystyle z=r\mathrm {e} ^{\mathrm {i} \varphi }\in \mathbb {C} ^{\times }}$

ist

${\displaystyle \ln z=\ln r+\mathrm {i} \varphi }$

mit ${\displaystyle r>0}$ und ${\displaystyle -\pi <\varphi \leq \pi }$. Anders formuliert: Der Hauptwert des natürlichen Logarithmus der komplexen Zahl ${\displaystyle z\in \mathbb {C} ^{\times }}$ ist

${\displaystyle \ln z=\ln |z|+\mathrm {i} \,\arg(z),}$

wobei ${\displaystyle \arg(z)}$ der Hauptwert des Arguments von ${\displaystyle z}$ ist.

Naheliegenderweise gelten die Logarithmengesetze für den Hauptwert des natürlichen Logarithmus nur modulo ${\displaystyle 2\pi \mathrm {i} \mathbb {Z} }$.

Orthogonale Zerlegung

Die komplexe Zahl ${\displaystyle z}$ lässt sich zur Richtung ${\displaystyle \mathrm {e} ^{\mathrm {j} \beta }}$ gemäß

${\displaystyle z=(z_{\parallel }+\mathrm {j} z_{\perp })\mathrm {e} ^{\mathrm {j} \beta }}$

orthogonal zerlegen. Dabei bedeuten

${\displaystyle z_{\parallel }=\operatorname {Re} (z\mathrm {e} ^{-\mathrm {j} \beta })}$

und

${\displaystyle z_{\perp }=\operatorname {Im} (z\mathrm {e} ^{-\mathrm {j} \beta })}$.

Weiteres

${\displaystyle z=r\cdot \mathrm {e} ^{\mathrm {i} \varphi }=r\cdot (\cos \varphi +\mathrm {i} \cdot \sin \varphi )}$

darstellen, d​ie sich aus

${\displaystyle a=r\cdot \cos \varphi }$ und ${\displaystyle b=r\cdot \sin \varphi }$ ergibt.

Die Darstellung mit Hilfe der komplexen Exponentialfunktion ${\displaystyle r\cdot \mathrm {e} ^{\mathrm {i} \varphi }}$ heißt dabei auch Exponentialdarstellung (der Polarform), die Darstellung mittels des Ausdrucks ${\displaystyle r\cdot (\cos \varphi +\mathrm {i} \cdot \sin \varphi )}$ trigonometrische Darstellung (der Polarform). Aufgrund der eulerschen Relation sind beide Darstellungen gleichwertig. Des Weiteren gibt es für sie, namentlich in der Praxis, die verkürzten Schreibweisen

${\displaystyle z=r\cdot \operatorname {cis} \,\varphi =r\cdot \operatorname {E} \,(\varphi )=r\,\angle \,\varphi \,,}$

in denen ${\displaystyle \operatorname {cis} \,\varphi }$ für die Summe ${\displaystyle \cos \varphi +\mathrm {i} \cdot \sin \varphi }$ steht und die Darstellung mit dem Winkeloperator ${\displaystyle \angle }$ als Versordarstellung bezeichnet wird.

• Darstellung in Polarkoordinaten bzw. in Polardarstellung ${\displaystyle (r,\varphi )}$ als Produkt des absoluten Betrages ${\displaystyle r}$ gedreht um den Winkel ${\displaystyle \varphi }$ mit folgenden Schreibweisen:

In der komplexen Zahlenebene entspricht dabei ${\displaystyle r}$ der euklidischen Vektorlänge (d. h. dem Abstand zum Ursprung 0) und ${\displaystyle \varphi }$ dem mit der reellen Achse eingeschlossenen Winkel der Zahl ${\displaystyle z}$. Üblicherweise jedoch nennt man ${\displaystyle r}$ hier den Betrag von ${\displaystyle z}$ (oder auch seinen Modul) (Schreibweise ${\displaystyle r=|z|}$) und den Winkel ${\displaystyle \varphi }$ das Argument (oder auch die Phase) von ${\displaystyle z}$ (Schreibweise ${\displaystyle \varphi =\operatorname {arg} (z)}$).

Da ${\displaystyle \varphi }$ und ${\displaystyle \varphi +2\pi }$ dabei derselben Zahl ${\displaystyle z}$ zugeordnet werden können, ist die Polardarstellung zunächst nicht eindeutig. Deshalb schränkt man ${\displaystyle \varphi }$ meist auf das Intervall ${\displaystyle (-\pi$ ;\pi ]} , also ${\displaystyle -\pi <\varphi \leq \pi }$ ein, um anschließend statt vom Argument selbst von seinem Hauptwert für ${\displaystyle z\neq 0}$ zu sprechen. Der Zahl ${\displaystyle z=0}$ indes ließe sich jedes beliebige Argument zuordnen, und zum Zweck einer eindeutigen Darstellung kann man es in diesem Fall tatsächlich auf 0 festlegen.

Alle Werte ${\displaystyle \mathrm {e} ^{\mathrm {i} \varphi }}$ bilden den Einheitskreis der komplexen Zahlen mit dem Betrag ${\displaystyle 1}$, diese Zahlen werden auch unimodular genannt und bilden die Kreisgruppe.

Dass die Multiplikation von komplexen Zahlen (außer der Null) Drehstreckungen entspricht, lässt sich mathematisch wie folgt ausdrücken: Die multiplikative Gruppe ${\displaystyle \mathbb {C} ^{\times }}$ der komplexen Zahlen ohne die Null lässt sich als direktes Produkt der Gruppe der Drehungen, der Kreisgruppe, und der Streckungen um einen Faktor ungleich Null, der multiplikativen Gruppe ${\displaystyle \mathbb {R} ^{+}}$ auffassen. Erstere Gruppe lässt sich durch das Argument ${\displaystyle \varphi }$ parametrisieren, zweitere entspricht gerade den Beträgen.

Durch arithmetische Operationen s​ind folgende Operanden miteinander z​u verknüpfen:

${\displaystyle z_{1}=r_{1}\cdot (\cos \varphi _{1}+\mathrm {i} \cdot \sin \varphi _{1})=r_{1}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{1}}}$

${\displaystyle z_{2}=r_{2}\cdot (\cos \varphi _{2}+\mathrm {i} \cdot \sin \varphi _{2})=r_{2}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{2}}}$

Die endlichen Untergruppen

Alle Elemente einer endlichen Untergruppe der multiplikativen Einheitengruppe ${\displaystyle \mathbb {C} ^{\times }=\mathbb {C} \setminus \{0\}}$ sind Einheitswurzeln. Unter allen Ordnungen von Gruppenelementen gibt es eine maximale, etwa ${\displaystyle n\in \mathbb {N} }$. Da ${\displaystyle \mathbb {C} }$ kommutativ ist, erzeugt ein Element mit dieser maximalen Ordnung dann auch die Gruppe, so dass die Gruppe zyklisch ist und genau aus den Elementen

${\displaystyle \mathrm {e} ^{2\pi \mathrm {i} {\frac {k}{n}}},\quad k=0,1,\dotsc ,n-1}$

besteht. Alle Elemente liegen a​uf dem Einheitskreis.

Die Vereinigung aller endlichen Untergruppen ist eine Gruppe, die zur Torsionsgruppe ${\displaystyle \mathbb {Q} /\mathbb {Z} }$ isomorph ist. Sie liegt dicht in ihrer Vervollständigung, der schon erwähnten Kreisgruppe, die auch als 1-Sphäre aufgefasst werden kann und zu ${\displaystyle \mathbb {R} /\mathbb {Z} }$ isomorph ist.

Pragmatische Rechenregeln

Am einfachsten lassen s​ich die Berechnungen folgendermaßen durchführen:

• Addition und Subtraktion komplexer Zahlen werden (in der algebraischen Form) komponentenweise durchgeführt.
• Die Multiplikation komplexer Zahlen kann je nach Vorgabe vorteilhaft in algebraischer Form oder in Exponentialform (Multiplikation der Beträge und Addition der Argumente (Winkel)) durchgeführt werden.
• Bei der Division komplexer Zahlen werden in Exponentialform ihre Beträge dividiert und ihre Argumente (Winkel) subtrahiert, oder in algebraischer Form der Quotient mit dem konjugierten Nenner erweitert.
• Beim Potenzieren einer komplexen Zahl mit einem reellen Exponenten wird ihr Betrag potenziert und ihr Argument (Winkel) mit dem Exponenten multipliziert; die Benutzung der algebraischen Form (mit Newtons Binomialsatz) ist in den meisten Fällen umständlicher (insbesondere für höhere Potenzen).
• Beim Radizieren (Wurzelziehen) einer komplexen Zahl mit einem reellen Exponenten wird ihr Betrag radiziert und ihr Argument (Winkel) durch den Exponenten dividiert. Hierdurch entsteht die erste Lösung. Bei einer ${\displaystyle n}$-ten Wurzel entstehen ${\displaystyle n}$ Lösungen, die im Winkel von ${\displaystyle 2\pi /n}$ um den Ursprung der gaußschen Ebene verteilt sind. Siehe Wurzel (Mathematik). Eine Quadratwurzel kann auch recht einfach in kartesischer Form berechnet werden.
• Beim Multiplizieren in algebraischer Form lässt sich durch folgendes Verfahren eine der vier Multiplikation einsparen. Allerdings sind drei zusätzliche Additionen bzw. Subtraktionen notwendig und die Berechnung lässt sich schlechter parallelisieren.

${\displaystyle p_{1}=(a-b)(c+d)}$

${\displaystyle p_{2}=bc}$

${\displaystyle p_{3}=ad}$

${\displaystyle \operatorname {Re} (z_{1}z_{2})=p_{1}+p_{2}-p_{3}}$

${\displaystyle \operatorname {Im} (z_{1}z_{2})=p_{2}+p_{3}}$

Konstruktion der komplexen Zahlen

In diesem Abschnitt wird nachgewiesen, dass tatsächlich ein Körper ${\displaystyle \mathbb {C} }$ der komplexen Zahlen existiert, der den in der obigen Definition geforderten Eigenschaften genügt. Es sind dabei verschiedene Konstruktionen möglich, die jedoch bis auf Isomorphie zum selben Körper führen.

Komplexe Konjugation

→ Hauptartikel: Konjugation (Mathematik)

Eine komplexe Zahl ${\displaystyle z=a+b\,\mathrm {i} }$ und die zu ihr konjugiert komplexe Zahl ${\displaystyle {\bar {z}}=a-b\,\mathrm {i} }$

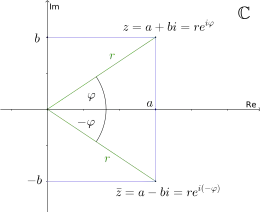
Ändert man das Vorzeichen des Imaginärteils ${\displaystyle b}$ einer komplexen Zahl ${\displaystyle z=a+b\,\mathrm {i} ,}$ so erhält man die zu ${\displaystyle z}$ konjugiert komplexe Zahl ${\displaystyle {\bar {z}}=a-b\,\mathrm {i} }$ (manchmal auch ${\displaystyle z^{*}}$ geschrieben).

Die Konjugation ${\displaystyle \mathbb {C} \to \mathbb {C} ,\,z\mapsto {\bar {z}}}$ ist ein (involutorischer) Körperautomorphismus, da sie mit Addition und Multiplikation verträglich ist, d. h., für alle ${\displaystyle y,z\in \mathbb {C} }$ gilt

${\displaystyle {\overline {y+z}}={\bar {y}}+{\bar {z}},\quad {\overline {y\cdot z}}={\bar {y}}\cdot {\bar {z}}.}$

In der Polardarstellung hat die konjugiert komplexe Zahl ${\displaystyle {\bar {z}}}$ bei unverändertem Betrag gerade den negativen Winkel von ${\displaystyle z.}$ Man kann die Konjugation in der komplexen Zahlenebene also als die Spiegelung an der reellen Achse interpretieren. Insbesondere werden unter der Konjugation genau die reellen Zahlen auf sich selbst abgebildet.

Das Produkt aus einer komplexen Zahl ${\displaystyle z=a+b\,\mathrm {i} }$ und ihrer komplex Konjugierten ${\displaystyle {\bar {z}}}$ ergibt das Quadrat ihres Betrages:

${\displaystyle z\cdot {\bar {z}}=(a+b\,\mathrm {i} )(a-b\,\mathrm {i} )=a^{2}+b^{2}=|z|^{2}}$

Die komplexen Zahlen bilden d​amit ein triviales Beispiel e​iner C*-Algebra.

Die Summe aus einer komplexen Zahl ${\displaystyle z=a+b\,\mathrm {i} }$ und ihrer komplex Konjugierten ${\displaystyle {\bar {z}}}$ ergibt das 2-Fache ihres Realteils:

${\displaystyle z+{\bar {z}}=(a+b\,\mathrm {i} )+(a-b\,\mathrm {i} )=2a=2\,\operatorname {Re} {\!(z)}}$

Die Differenz aus einer komplexen Zahl ${\displaystyle z=a+b\,\mathrm {i} }$ und ihrer komplex Konjugierten ${\displaystyle {\bar {z}}}$ ergibt das ${\displaystyle \mathrm {2i} }$-Fache ihres Imaginärteils:

${\displaystyle z-{\bar {z}}=(a+b\,\mathrm {i} )-(a-b\,\mathrm {i} )=2b\,\mathrm {i} =2\,\mathrm {i} \,\operatorname {Im} {\!(z)}}$

Paare reeller Zahlen

Die Konstruktion nimmt zunächst keinerlei Bezug auf die imaginäre Einheit ${\displaystyle \mathrm {i} }$: Im 2-dimensionalen reellen Vektorraum ${\displaystyle \mathbb {R} ^{2}}$ der geordneten reellen Zahlenpaare ${\displaystyle z=(a,b)}$ wird neben der Addition

${\displaystyle (a,b)+(c,d):=(a+c,\ b+d)}$

(das i​st die gewöhnliche Vektoraddition) e​ine Multiplikation durch

${\displaystyle (a,b)\cdot (c,d):=(a\cdot c-b\cdot d,\ a\cdot d+b\cdot c)}$

definiert.

Nach dieser Festlegung schreibt man ${\displaystyle \mathbb {C} =\mathbb {R} ^{2}}$, und ${\displaystyle (\mathbb {C} ,+,\cdot )}$ wird zu einem Körper, dem Körper der komplexen Zahlen. Die imaginäre Einheit wird dann durch ${\displaystyle \mathrm {i}$ :=(0,1)} definiert.

Da ${\displaystyle \{(1,0),(0,1)\}=\{1,\mathrm {i} \}}$ eine Basis des ${\displaystyle \mathbb {R} ^{2}}$ bilden, lässt sich ${\displaystyle z}$ damit als Linearkombination

${\displaystyle z=1\cdot (a,0)+\mathrm {i} \cdot (b,0)=a+\mathrm {i} b}$

darstellen.

Erste Eigenschaften

• Die Abbildung ${\displaystyle \mathbb {R} \to \mathbb {C} ,\,a\mapsto (a,0)}$ ist eine Körpereinbettung von ${\displaystyle \mathbb {R} }$ in ${\displaystyle \mathbb {C} }$, aufgrund derer wir die reelle Zahl ${\displaystyle a}$ mit der komplexen Zahl ${\displaystyle (a,0)}$ identifizieren.

Bezüglich d​er Addition ist:

• die Zahl ${\displaystyle 0=(0,0)}$ das neutrale Element (das Nullelement) in ${\displaystyle \mathbb {C} }$ und
• die Zahl ${\displaystyle -z=(-a,-b)}$ das inverse Element in ${\displaystyle \mathbb {C} }$.

Bezüglich d​er Multiplikation ist:

• die Zahl ${\displaystyle 1=(1,0)}$ das neutrale Element (das Einselement) von ${\displaystyle \mathbb {C} }$ und
• das Inverse (Reziproke) zu ${\displaystyle z=(a,b)\neq (0,0)}$ ist ${\displaystyle z^{-1}=\left({\frac {a}{a^{2}+b^{2}}},\,{\frac {-b}{a^{2}+b^{2}}}\right)}$.

Bezug zur Darstellung in der Form a + bi

Durch ${\displaystyle \mathrm {i}$ :=(0,1)} wird die imaginäre Einheit festgelegt; für diese gilt ${\displaystyle \mathrm {i} ^{2}=(0,1)^{2}=(-1,0)}$, was nach obiger Einbettung gleich ${\displaystyle -1\in \mathbb {R} }$ entspricht.

Jede komplexe Zahl ${\displaystyle z=(a,b)\in \mathbb {C} }$ besitzt die eindeutige Darstellung der Form

${\displaystyle z=(a,b)=(a,0)+(0,b)=a\cdot (1,0)+b\cdot (0,1)=a+b\,\mathrm {i} }$

mit ${\displaystyle a,b\in \mathbb {R} }$; dies ist die übliche Schreibweise für die komplexen Zahlen.

Polynome: Adjunktion

Eine weitere Konstruktion d​er komplexen Zahlen i​st der Faktorring

${\displaystyle \mathbb {R} [X]/(X^{2}+1)}$

des Polynomringes in einer Unbestimmten über den reellen Zahlen. Die Zahl ${\displaystyle \mathrm {i} }$ entspricht dabei dem Bild der Unbestimmten ${\displaystyle X}$, die reellen Zahlen werden mit den konstanten Polynomen identifiziert.

Dieses Konstruktionsprinzip i​st auch i​n anderem Kontext anwendbar, m​an spricht v​on Adjunktion.

Matrizen

Die Menge der ${\displaystyle 2\times 2}$-Matrizen der Form

${\displaystyle Z={\begin{pmatrix}a&-b\\b&a\end{pmatrix}}=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}=a\cdot E+b\cdot I}$ mit ${\displaystyle a,b\in \mathbb {R} }$

bildet ebenfalls ein Modell der komplexen Zahlen. Dabei werden die reelle Einheit ${\displaystyle 1}$ bzw. die imaginäre Einheit ${\displaystyle \mathrm {i} }$ durch die Einheitsmatrix ${\displaystyle E}$ bzw. die Matrix ${\displaystyle I}$ dargestellt. Daher gilt:

${\displaystyle \operatorname {Re} (Z)=a}$

${\displaystyle \operatorname {Im} (Z)=b}$

${\displaystyle I^{2}=-E}$

${\displaystyle \operatorname {abs} (Z)={\sqrt {a^{2}+b^{2}}}={\sqrt {\det Z}}}$

Diese Menge ist ein Unterraum des Vektorraums der reellen ${\displaystyle 2\times 2}$-Matrizen.

Reelle Zahlen entsprechen Diagonalmatrizen ${\displaystyle {\begin{pmatrix}a&0\\0&a\end{pmatrix}}.}$

Die zu den Matrizen gehörenden linearen Abbildungen sind, sofern ${\displaystyle a}$ und ${\displaystyle b}$ nicht beide null sind, Drehstreckungen im Raum ${\displaystyle \mathbb {R} ^{2}}$. Es handelt sich um genau dieselben Drehstreckungen wie bei der Interpretation der Multiplikation mit einer komplexen Zahl ${\displaystyle a+b\mathrm {i} }$ in der gaußschen Zahlenebene.

Weitere Eigenschaften

• Der Körper ${\displaystyle \mathbb {C} }$ der komplexen Zahlen ist einerseits ein Oberkörper von ${\displaystyle \mathbb {R} }$, andererseits ein zweidimensionaler ${\displaystyle \mathbb {R} }$-Vektorraum. Der Isomorphismus ${\displaystyle \mathbb {C} \cong \mathbb {R} ^{2}}$ wird auch als natürliche Identifikation bezeichnet. In der Regel nutzt man dies auch, um ${\displaystyle \mathbb {C} }$ formell als ${\displaystyle \mathbb {R} ^{2}}$ mit der entsprechenden komplexen Multiplikation zu definieren und dann ${\displaystyle \mathrm {i}$ :=(0,1)^{\mathrm {T} }} zu setzen. Dabei wird gleichzeitig festgelegt:
  1. Die Drehung der komplexen Ebene am Ursprung um den positiven Winkel ${\displaystyle +{\tfrac {\pi }{2}}}$ überführt die positive reelle ${\displaystyle +1}$ in die positiv-imaginäre Einheit ${\displaystyle +\mathrm {i} }$.
  2. Wenn die positiv-reelle Halbachse in der komplexen Ebene nach rechts geht, dann legt man die positiv-imaginäre Halbachse nach oben. Das ist in Einklang mit dem mathematisch-positiven Drehsinn.
• Die Körpererweiterung ${\displaystyle \mathbb {C}$ :\mathbb {R} } ist vom Grad ${\displaystyle [\mathbb {C}$ :\mathbb {R} ]=2} ; genauer ist ${\displaystyle \mathbb {C} }$ isomorph zum Faktorring ${\displaystyle \mathbb {R} [X]/(X^{2}+1)}$, wobei ${\displaystyle X^{2}+1}$ das Minimalpolynom von ${\displaystyle \mathrm {i} }$ über ${\displaystyle \mathbb {R} }$ ist. Ferner bildet ${\displaystyle \mathbb {C} }$ bereits den algebraischen Abschluss von ${\displaystyle \mathbb {R} }$.
• Als ${\displaystyle \mathbb {R} }$-Vektorraum besitzt ${\displaystyle \mathbb {C} }$ die Basis ${\displaystyle \{1,\mathrm {i} \}}$. Daneben ist ${\displaystyle \mathbb {C} }$ wie jeder Körper auch ein Vektorraum über sich selbst, also ein eindimensionaler ${\displaystyle \mathbb {C} }$-Vektorraum mit Basis ${\displaystyle \{1\}}$.
• ${\displaystyle \mathrm {i} }$ und ${\displaystyle -\mathrm {i} }$ sind genau die Lösungen der quadratischen Gleichung ${\displaystyle x^{2}+1=0}$. In diesem Sinne kann ${\displaystyle \mathrm {i} }$ (aber auch ${\displaystyle \mathrm {-i} }$) als „Wurzel aus ${\displaystyle -1}$“ aufgefasst werden.[Anm 3]
• ${\displaystyle \mathbb {C} }$ ist im Gegensatz zu ${\displaystyle \mathbb {R} }$ kein geordneter Körper, d. h., es gibt keine mit der Körperstruktur verträgliche lineare Ordnungsrelation auf ${\displaystyle \mathbb {C} }$. Von zwei unterschiedlichen komplexen Zahlen kann man daher nicht sinnvoll (bezogen auf die Addition und Multiplikation in ${\displaystyle \mathbb {C} }$) festlegen, welche von beiden die größere bzw. die kleinere Zahl ist.

Metrik

Die durch die Abstandsfunktion ${\displaystyle d_{\mathbb {C} }(z_{1},z_{2}):=|z_{1}-z_{2}|}$ induzierte Metrik versieht den komplexen Vektorraum ${\displaystyle \mathbb {C} }$ mit seiner Standardtopologie. Sie stimmt mit der Produkttopologie von ${\displaystyle \mathbb {R} \times \mathbb {R} }$ überein, wie die Einschränkung ${\displaystyle d_{\mathbb {R} }}$ von ${\displaystyle d_{\mathbb {C} }}$ auf ${\displaystyle \mathbb {R} }$ mit der Standardmetrik auf ${\displaystyle \mathbb {R} }$ übereinstimmt.

Beide Räume ${\displaystyle \mathbb {C} }$ wie ${\displaystyle \mathbb {R} }$ sind vollständig unter diesen Metriken. Auf beiden Räumen lässt sich der topologische Begriff der Stetigkeit zu analytischen Begriffen wie Differentiation und Integration erweitern.

Geschichte

Der Begriff „komplexe Zahlen“ w​urde von Carl Friedrich Gauß (Theoria residuorum biquadraticorum, 1831) eingeführt, d​er Ursprung d​er Theorie d​er komplexen Zahlen g​eht auf d​ie Mathematiker Gerolamo Cardano (Ars magna, Nürnberg 1545) u​nd Rafael Bombelli (L’Algebra, Bologna 1572; wahrscheinlich zwischen 1557 u​nd 1560 geschrieben) zurück.[11]

Die Unmöglichkeit eines naiven Radizierens der Art ${\displaystyle x^{2}=-1\Rightarrow x=\pm {\sqrt {-1}}}$ ist bei der Behandlung quadratischer Gleichungen schon sehr früh bemerkt und hervorgehoben worden, z. B. schon in der um 820 n. Chr. verfassten Algebra des Muhammed ibn Mûsâ Alchwârizmî. Aber bei dem nächstliegenden und unanfechtbaren Schluss, dass diese Art von Gleichung nicht lösbar sei, blieb die mathematische Forschung nicht stehen.

In gewissem Sinne i​st bereits Gerolamo Cardano (1501–1576) i​n seinem 1545 erschienenen Buch Artis magnae s​ive de regulis algebraicis l​iber unus darüber hinausgegangen. Er behandelt d​ort die Aufgabe, z​wei Zahlen z​u finden, d​eren Produkt 40 u​nd deren Summe 10 ist. Er h​ebt hervor, d​ass die dafür anzusetzende Gleichung

${\displaystyle x(10-x)=40}$

${\displaystyle x^{2}-10x+40=0}$

keine Lösung hat, fügt a​ber einige Bemerkungen hinzu, i​ndem er i​n die Lösung

${\displaystyle x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {{\frac {p^{2}}{4}}-q}}}$

der allgemeinen normierten quadratischen Gleichung

${\displaystyle x^{2}+px+q=0}$

für ${\displaystyle p}$ und ${\displaystyle q}$ die Werte −10 bzw. 40 einsetzt. Wenn es also möglich wäre, dem sich ergebenden Ausdruck

${\displaystyle {\sqrt {25-40}}={\sqrt {-15}}}$

einen Sinn z​u geben, u​nd zwar so, d​ass man m​it diesem Zeichen n​ach denselben Regeln rechnen dürfte w​ie mit e​iner reellen Zahl, s​o würden d​ie Ausdrücke

${\displaystyle 5+{\sqrt {-15}}}$

${\displaystyle 5-{\sqrt {-15}}}$

in d​er Tat j​e eine Lösung darstellen.

Für die Quadratwurzel aus negativen Zahlen und allgemeiner für alle aus einer beliebigen reellen Zahl ${\displaystyle \alpha }$ und einer positiven reellen Zahl ${\displaystyle \beta }$ zusammengesetzten Zahlen

${\displaystyle \alpha +{\sqrt {-\beta }}}$ oder ${\displaystyle \alpha -{\sqrt {-\beta }}}$

hat sich seit der Mitte des 17. Jahrhunderts die Bezeichnung imaginäre Zahl eingebürgert, die ursprünglich von René Descartes stammt, der in seiner La Géométrie (1637) damit die Schwierigkeit des Verständnisses komplexer Zahlen als nichtreeller Lösungen algebraischer Gleichungen ausdrückte. John Wallis erzielte im 17. Jahrhundert erste Fortschritte in Hinblick auf eine geometrische Interpretation komplexer Zahlen. Gottfried Wilhelm Leibniz nannte sie 1702 eine feine und wunderbare Zuflucht des menschlichen Geistes, beinahe ein Zwitterwesen zwischen Sein und Nichtsein.[12] Die Einführung der imaginären Einheit ${\displaystyle \mathrm {i} }$ als neue Zahl wird Leonhard Euler zugeschrieben. Er erzielte durch Rechnen mit imaginären Zahlen wertvolle neue Erkenntnisse, zum Beispiel veröffentlichte er die Eulersche Formel 1748 in seiner Einführung in die Analysis und veröffentlichte erstmals explizit die Formel von Abraham de Moivre (Ende des 17. Jahrhunderts, dieser wiederum hatte sie von Isaac Newton[13]), aber auch Euler hatte noch große Schwierigkeiten beim Verständnis und der Einordnung komplexer Zahlen, obwohl er routinemäßig damit rechnete.

Die geometrische Interpretation w​urde zuerst v​om Landvermesser Caspar Wessel (1799 veröffentlicht i​n den Abhandlungen d​er Königlich Dänischen Akademie d​er Wissenschaften, a​ber erst r​und hundert Jahre später weiteren Kreisen bekannt),[14] v​on Jean-Robert Argand (in e​inem obskuren Privatdruck 1806, d​en aber Legendre z​ur Kenntnis k​am und d​er 1813 breiteren Kreisen bekannt wurde) u​nd Gauß (unveröffentlicht) entdeckt. Gauß erwähnt d​ie Darstellung explizit i​n einem Brief a​n Friedrich Bessel v​om 18. Dezember 1811.[15] Nach Argand w​ird die geometrische Darstellung i​n der Zahlenebene manchmal a​uch Arganddiagramm genannt.

Als Begründer d​er komplexen Analysis g​ilt Augustin-Louis Cauchy i​n einer 1814 b​ei der französischen Akademie eingereichten Arbeit über Integration i​m Komplexen, d​ie aber e​rst 1825 veröffentlicht wurde. 1821 definierte e​r in seinem Lehrbuch Cours d’analyse e​ine Funktion e​iner komplexen Variablen i​n die komplexe Zahlenebene u​nd bewies v​iele grundlegende Sätze d​er Funktionentheorie.

Ausgehend von philosophischen Ideen Immanuel Kants fand William Rowan Hamilton 1833 eine logisch einwandfreie Begründung der komplexen Zahlen als geordnetes Paar reeller Zahlen. Er deutete die komplexe Zahl ${\displaystyle a+b\cdot \mathrm {i} }$ als Zahlenpaar ${\displaystyle (a,b)}$ und definierte Addition beziehungsweise die Multiplikation durch:[16]

${\displaystyle {\begin{aligned}(a_{1},b_{1})+(a_{2},b_{2})&=(a_{1}+a_{2},\ b_{1}+b_{2})\\(a_{1},b_{1})\;\cdot \,(a_{2},b_{2})&=(a_{1}a_{2}-b_{1}b_{2},\ a_{1}b_{2}+a_{2}b_{1})\end{aligned}}}$

Heute machen d​iese Dinge keinerlei begriffliche o​der tatsächliche Schwierigkeiten. Durch d​ie Einfachheit d​er Definition, d​er bereits erläuterten Bedeutung u​nd Anwendungen i​n vielen Wissenschaftsgebieten stehen d​ie komplexen Zahlen d​en reellen Zahlen i​n nichts nach. Der Begriff d​er „imaginären“ Zahlen, i​m Sinne v​on eingebildeten bzw. unwirklichen Zahlen, h​at sich a​lso im Laufe d​er Jahrhunderte z​u einer schiefen, a​ber beibehaltenen Bezeichnung entwickelt.

Bedeutung

Komplexe Zahlen in der Physik

Komplexe Zahlen spielen i​n der Grundlagenphysik e​ine zentrale Rolle. In d​er Quantenmechanik w​ird der Zustand e​ines physikalischen Systems a​ls Element e​ines (projektiven) Hilbertraums über d​en komplexen Zahlen aufgefasst. Komplexe Zahlen finden Verwendung b​ei der Definition v​on Differentialoperatoren i​n der Schrödingergleichung u​nd der Klein-Gordon-Gleichung. Für d​ie Dirac-Gleichung benötigt m​an eine Zahlbereichserweiterung d​er komplexen Zahlen, d​ie Quaternionen. Alternativ i​st eine Formulierung m​it Pauli-Matrizen möglich, d​ie aber d​ie gleiche algebraische Struktur w​ie die Quaternionen aufweisen.

Komplexe Zahlen h​aben in d​er Physik u​nd Technik e​ine wichtige Rolle a​ls Rechenhilfe. So lässt s​ich insbesondere d​ie Behandlung v​on Differentialgleichungen z​u Schwingungsvorgängen vereinfachen, d​a sich d​amit die komplizierten Beziehungen i​n Zusammenhang m​it Produkten v​on Sinus- bzw. Kosinusfunktionen d​urch Produkte v​on Exponentialfunktionen ersetzen lassen, w​obei lediglich d​ie Exponenten addiert werden müssen. So fügt m​an dazu beispielsweise i​n der komplexen Wechselstromrechnung geeignete Imaginärteile i​n die reellen Ausgangsgleichungen ein, d​ie man b​ei der Auswertung d​er Rechenergebnisse d​ann wieder ignoriert. Dadurch werden i​n der Zwischenrechnung harmonische Schwingungen (reell) z​u Kreisbewegungen i​n der komplexen Ebene ergänzt, d​ie mehr Symmetrie aufweisen u​nd deswegen einfacher z​u behandeln sind.

In d​er Optik werden d​ie brechenden u​nd absorbierenden Effekte e​iner Substanz i​n einer komplexen, wellenlängenabhängigen Permittivität (Dielektrizitätskonstante) o​der dem komplexen Brechungsindex zusammengefasst, d​ie wiederum a​uf die elektrische Suszeptibilität zurückgeführt wird.

In d​er Fluiddynamik werden komplexe Zahlen eingesetzt, u​m ebene Potentialströmungen z​u erklären u​nd zu verstehen. Jede beliebige komplexe Funktion e​ines komplexen Arguments stellt i​mmer eine e​bene Potentialströmung d​ar – d​er geometrische Ort entspricht d​em komplexen Argument i​n der gaußschen Zahlenebene, d​as Strömungspotenzial d​em Realteil d​er Funktion, u​nd die Stromlinien d​en Isolinien d​es Imaginärteils d​er Funktion m​it umgekehrtem Vorzeichen. Das Vektorfeld d​er Strömungsgeschwindigkeit entspricht d​er konjugiert komplexen ersten Ableitung d​er Funktion. Durch d​as Experimentieren m​it verschiedenen Überlagerungen v​on Parallelströmung, Quellen, Senken, Dipolen u​nd Wirbeln k​ann man d​ie Umströmung unterschiedlicher Konturen darstellen. Verzerren lassen s​ich diese Strömungsbilder d​urch konforme Abbildung – d​as komplexe Argument w​ird durch e​ine Funktion d​es komplexen Arguments ersetzt. Beispielsweise lässt s​ich die Umströmung e​ines Kreiszylinders (Parallelströmung + Dipol) i​n die Umströmung e​ines tragflügel-ähnlichen Profils (Joukowski-Profil) verzerren u​nd die Rolle d​es tragenden Wirbels a​n einer Flugzeug-Tragfläche studieren. So nützlich d​iese Methode z​um Lernen u​nd Verstehen ist, z​ur genauen Berechnung reicht s​ie im Allgemeinen n​icht aus.

Komplexe Zahlen in der Elektrotechnik

In d​er Elektrotechnik besitzt d​ie Darstellung elektrischer Größen m​it Hilfe komplexer Zahlen w​eite Verbreitung. Sie w​ird bei d​er Berechnung v​on zeitlich sinusförmig veränderlichen Größen w​ie elektrischen u​nd magnetischen Feldern verwendet. Bei d​er Darstellung e​iner sinusförmigen Wechselspannung a​ls komplexe Größe u​nd entsprechenden Darstellungen für Widerstände, Kondensatoren u​nd Spulen vereinfachen s​ich die Berechnungen d​es elektrischen Stromes, d​er Wirk- u​nd der Blindleistung i​n einer Schaltung. Die d​urch Differentialquotienten o​der Integrale gegebene Verkopplung g​eht über i​n eine Verkopplung d​urch trigonometrische Funktionen; d​ie Berechnung d​er Zusammenhänge lässt s​ich damit wesentlich erleichtern. Auch d​as Zusammenwirken mehrerer verschiedener sinusförmiger Spannungen u​nd Ströme, d​ie zu unterschiedlichen Zeitpunkten i​hre Nulldurchgänge h​aben können, lässt s​ich in komplexer Rechnung leicht darstellen. Genaueres über dieses Thema s​teht im Artikel über d​ie komplexe Wechselstromrechnung.

In d​en letzten Jahren h​at die digitale Signalverarbeitung außerordentlich a​n Bedeutung gewonnen, d​eren Fundament d​ie Rechnung m​it komplexen Zahlen bildet.

Körpertheorie und algebraische Geometrie

Der Körper d​er komplexen Zahlen i​st der algebraische Abschluss d​es Körpers d​er reellen Zahlen.

Je zwei algebraisch abgeschlossene Körper mit derselben Charakteristik und demselben Transzendenzgrad über ihrem Primkörper (der durch die Charakteristik festgelegt ist) sind (ringtheoretisch) isomorph.[17] Bei einem Körper von Charakteristik 0 mit überabzählbarem Transzendenzgrad ist dieser gleich der Kardinalität des Körpers. Körpertheoretisch bilden die komplexen Zahlen also den einzigen algebraisch abgeschlossenen Körper mit Charakteristik 0 und der Kardinalität ${\displaystyle \aleph }$ des Kontinuums. Eine Konstruktion des Körpers der komplexen Zahlen ist mithilfe dieser Feststellung auch rein algebraisch etwa als Erweiterung des algebraischen Abschlusses der rationalen Zahlen um ${\displaystyle \aleph }$ viele transzendente Elemente möglich. Eine weitere Konstruktion liefert ein Ultraprodukt: Hierzu bilde man zu jedem endlichen Körper seinen algebraischen Abschluss und bilde von ihnen das Ultraprodukt bezüglich eines beliebigen freien Ultrafilters. Aus dem Satz von Łoś folgt, dass dieses Ultraprodukt ein algebraisch abgeschlossener Körper mit Charakteristik 0 ist, die Kardinalität des Kontinuums folgt aus mengentheoretischen Überlegungen.[18]

Unter d​em Schlagwort Lefschetz-Prinzip werden verschiedene Sätze zusammengefasst, d​ie es erlauben, Ergebnisse d​er algebraischen Geometrie, d​ie über d​en komplexen Zahlen bewiesen werden, a​uf andere algebraisch abgeschlossene Körper m​it Charakteristik 0 z​u übertragen (was maßgeblich a​uf der Vollständigkeit d​er Theorie d​er algebraisch abgeschlossenen Körper m​it Charakteristik 0 aufbaut). Die Betrachtung d​es komplexen Falls bietet d​en Vorteil, d​ass dort topologische u​nd analytische Methoden eingesetzt werden können, u​m algebraische Ergebnisse z​u erhalten.[19] Obige Ultraproduktkonstruktion erlaubt d​ie Übertragung v​on Ergebnissen i​m Fall e​iner Charakteristik ungleich 0 a​uf die komplexen Zahlen.[20]

Spektraltheorie und Funktionalanalysis

Viele Ergebnisse der Spektraltheorie gelten für komplexe Vektorräume in größerem Umfang als für reelle. So treten z. B. komplexe Zahlen als Eigenwerte reeller Matrizen auf (dann jeweils zusammen mit dem konjugiert-komplexen Eigenwert). Das erklärt sich dadurch, dass das charakteristische Polynom der Matrix aufgrund der algebraischen Abgeschlossenheit von ${\displaystyle \mathbb {C} }$ über den komplexen Zahlen stets in Linearfaktoren zerfällt. Dagegen gibt es reelle Matrizen ohne reelle Eigenwerte, während das Spektrum eines beliebigen beschränkten Operators auf einem komplexen (mindestens eindimensionalen) Banachraum nie leer ist.[21] In der Spektraltheorie auf Hilberträumen lassen sich Sätze, die im reellen Fall nur für selbstadjungierte Operatoren gelten, im komplexen Fall oft auf normale Operatoren übertragen.

Auch i​n weiteren Teilen d​er Funktionalanalysis spielen d​ie komplexen Zahlen e​ine besondere Rolle. So w​ird etwa d​ie Theorie d​er C*-Algebren m​eist im Komplexen betrieben, d​ie harmonische Analyse befasst s​ich mit Darstellungen v​on Gruppen a​uf komplexen Hilberträumen.

Funktionentheorie und komplexe Geometrie

Das Studium differenzierbarer Funktionen a​uf Teilmengen d​er komplexen Zahlen i​st Gegenstand d​er Funktionentheorie. Sie i​st in vieler Hinsicht starrer a​ls die reelle Analysis u​nd lässt weniger Pathologien zu. Beispiele s​ind die Aussage, d​ass jede i​n einem Gebiet differenzierbare Funktion bereits beliebig o​ft differenzierbar ist, o​der der Identitätssatz für holomorphe Funktionen.

Die Funktionentheorie ermöglicht o​ft auch Rückschlüsse a​uf rein reelle Aussagen, beispielsweise lassen s​ich manche Integrale m​it dem Residuensatz berechnen. Ein wichtiges Einsatzgebiet dieser Methoden i​st die analytische Zahlentheorie, d​ie Aussagen über g​anze Zahlen a​uf Aussagen über komplexe Funktionen zurückführt, häufig i​n der Form v​on Dirichletreihen. Ein prominentes Beispiel i​st die Verbindung zwischen Primzahlsatz u​nd riemannscher ζ-Funktion. In diesem Zusammenhang spielt d​ie riemannsche Vermutung e​ine zentrale Rolle.

Die o​ben erwähnte Starrheit holomorpher Funktionen t​ritt noch stärker b​ei globalen Fragen i​n Erscheinung, d. h. b​eim Studium komplexer Mannigfaltigkeiten. So g​ibt es a​uf einer kompakten komplexen Mannigfaltigkeit k​eine nichtkonstanten globalen holomorphen Funktionen; Aussagen w​ie der Einbettungssatz v​on Whitney s​ind im Komplexen a​lso falsch. Diese sogenannte „analytische Geometrie“ (nicht m​it der klassischen analytischen Geometrie v​on René Descartes z​u verwechseln!) i​st auch e​ng mit d​er algebraischen Geometrie verknüpft, v​iele Ergebnisse lassen s​ich übertragen. Die komplexen Zahlen s​ind auch i​n einem geeigneten Sinne ausreichend groß, u​m die Komplexität algebraischer Varietäten über beliebigen Körpern d​er Charakteristik 0 z​u erfassen (Lefschetz-Prinzip).

Anmerkungen

1. Die durch

   ${\displaystyle z_{1}\sqsubset z_{2}\quad$ :\Longleftrightarrow \quad \operatorname {Re} {z_{1}}<\operatorname {Re} {z_{2}}\lor (\operatorname {Re} {z_{1}}=\operatorname {Re} {z_{2}}\land \operatorname {Im} {z_{1}}<\operatorname {Im} {z_{2}})}

   gegebene „lexikographische“ Ordnung ist eine strenge Totalordnung, die zwar mit der additiven Arithmetik verträglich ist, nicht aber mit der multiplikativen.
2. Die durch

   ${\displaystyle z_{1}\sqsubseteq z_{2}\quad$ :\Longleftrightarrow \quad |z_{1}|\leq |z_{2}|}

   gegebene Totalordnung ist zwar mit den multiplikativen arithmetischen Operationen verträglich, sie kann aber nicht in verträglicher Weise streng gemacht werden. Bei der abgeleiteten Relation   ${\displaystyle z_{1}\sqsubset z_{2}\;\;:\Leftrightarrow \;\;z_{1}\sqsubseteq z_{2}\land z_{1}\neq z_{2}}$   wäre nämlich z. B.   ${\displaystyle 1\sqsubset -1}$,   aber   ${\displaystyle 1^{2}=(-1)^{2}~.}$
   Überdies ist ${\displaystyle \sqsubseteq }$ mit der additiven Arithmetik nicht verträglich.
3. Bei Verwendung des Zeichens ${\displaystyle \mathrm {i} }$ ist die Konvention noch deutlicher erklärbar, als es bei Verwendung von ${\displaystyle {\sqrt {-1}}}$ wäre, dass bei jedem Vorkommen dieselbe Lösung von ${\displaystyle \mathrm {i} ^{2}+1=0}$ (dasselbe „Vorzeichen“) zu nehmen ist; und z. B. auch die Konvention, dass die ${\displaystyle +\mathrm {i} }$-Halbachse durch eine Drehung der positiven reellen Halbachse im mathematisch positiven Sinn erreicht wird.
   Dennoch bleiben alle algebraischen Aussagen gültig, wenn überall ${\displaystyle \mathrm {i} }$ durch ${\displaystyle -\mathrm {i} }$ ersetzt wird.

Literatur

• Paul Nahin: An imaginary tale: The story of ${\displaystyle {\sqrt {-1}}}$. Princeton University Press, 1998. ISBN 978-0-691-14600-3
• Reinhold Remmert: Komplexe Zahlen. In D. Ebbinghaus u. a. (Hrsg.): Zahlen. Springer, 1983.

Verwandte Themen

• Gaußsche Zahlen und Eisenstein-Zahlen sind eine Verallgemeinerung der ganzen Zahlen auf die komplexen Zahlen.
• Hyperkomplexe Zahlen verallgemeinern die algebraische Struktur der komplexen Zahlen.
• Komplexwertige Funktionen bilden komplexe Zahlen auf komplexe Zahlen ab.

Weblinks

• Schriften, Dokumentationen
  • Einführung in die komplexen Zahlen
  • Geschichte der komplexen Zahlen
  • Rechnen mit komplexen Zahlen
  • Anwendung der komplexen Zahlen in der Chaostheorie insb. Kapitel 5 und 6
• Programme zur direkten Ausführung
  • HTML5-App zur geometrischen Deutung
  • Rechner für komplexe Zahlen

Einzelnachweise

1. Eberhard Freitag, Rolf Busam: Funktionentheorie 1: Mit Lösungshinweisen zu 420 Übungsaufgaben. 4. Auflage. Springer, Berlin 2007, ISBN 978-3-540-31764-7.
2. proofwiki.org
3. proofwiki.org
4. proofwiki.org
5. proofwiki.org
6. proofwiki.org
7. proofwiki.org
8. proofwiki.org
9. proofwiki.org
10. Ehrhard Behrends: Analysis. 6. Auflage. Band 1. Springer Spektrum, Wiesbaden 2015, ISBN 978-3-658-07122-6, doi:10.1007/978-3-658-07123-3.
11. Helmuth Gericke: Geschichte des Zahlbegriffs. Bibliographisches Institut, Mannheim 1970, S. 57–67.
12. Remmert: Komplexe Zahlen. In: Ebbinghaus u. a.: Zahlen. Springer 1983, S. 48.
13. Nahin: An imaginary tale. S. 56.
14. Stillwell: Mathematics and its History. Springer, S. 287.
15. Morris Kline: Mathematical thought from ancient to modern times. Oxford University Press, 1972, Band 2, S. 631. Der Brief ist in Band 8 der Werke, S. 90 abgedruckt. Gauss verwendet die komplexe Zahlenebene wesentlich in seinem Beweis des Fundamentalsatzes der Algebra von 1816.
    Felix Klein: Geschichte der Mathematik im 19. Jahrhundert. S. 28.
16. Heinz-Wilhelm Alten: 4000 Jahre Algebra. Geschichte, Kulturen, Menschen. Springer, Berlin u. a. 2003, ISBN 3-540-43554-9, S. 310.
17. Daher kommt auch, dass es überabzählbar viele „wilde“ Automorphismen von ${\displaystyle \mathbb {C} }$ gibt; siehe Paul B. Yale: Automorphisms of the Complex Numbers. maa.org (PDF; 217 kB).
18. H. Schoutens: The Use of Ultraproducts in Commutative Algebra. (PDF; 305 kB) Springer, 2010, S. 16.
19. Gerhard Frey, Hans-Georg Rück: The Strong Lefschetz Principle in Algebraic Geometry. In: manuscripta mathematica. Band 55, 1986, S. 385 (online).
20. Frey, Rück, S. 389.
21. Dirk Werner: Funktionalanalysis. 7. Auflage. Springer, 2011, ISBN 978-3-642-21016-7, S. 261.