Siedepunkt
Der Siedepunkt (Abkürzung: Sdp.), Verdampfungspunkt oder auch Kochpunkt (Abkürzung: Kp.) eines Reinstoffes ist ein Wertepaar in dessen Phasendiagramm und besteht aus zwei Größen: der Sättigungstemperatur (speziell auch Siedetemperatur) und dem Sättigungsdampfdruck (speziell auch Siededruck) an der Phasengrenzlinie zwischen Gas und Flüssigkeit. Er setzt sich also aus den beiden Zustandsgrößen Druck und Temperatur beim Übergang eines Stoffes vom flüssigen in den gasförmigen Aggregatzustand zusammen. Bei einer offenen Flüssigkeit ist der Siedepunkt daher der Punkt auf der Temperaturskala, bei der der Dampfdruck gleich dem atmosphärischen Druck ist.
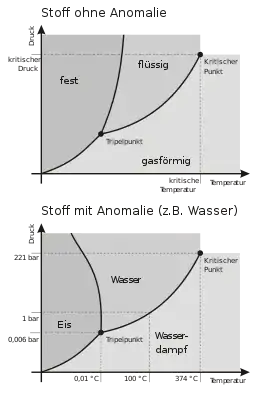
Der Siedepunkt stellt die Bedingungen dar, die beim Phasenübergang eines Stoffes von der flüssigen in die gasförmige Phase vorliegen, was man als Sieden bezeichnet.[1] Zudem ist er für den umgekehrten Vorgang der Kondensation, allerdings nur bei Reinstoffen, identisch mit dem Kondensationspunkt. Beim Verdampfen eines Stoffgemisches kommt es zu einem veränderten Siedeverhalten, und man beobachtet einen Siedebereich anstatt eines einzelnen Siedepunktes. Bei einem Phasenübergang von der flüssigen in die gasförmige Phase unterhalb des Siedepunktes spricht man von einer Verdunstung.
In Tabellenwerken werden die Siedetemperaturen bei Normaldruck angegeben, also bei 1013,25 hPa. Dieser Siedepunkt wird als Normalsiedepunkt[2], die angegebene Siedetemperatur als Normalsiedetemperatur (TSied) bezeichnet. Ein Verfahren zu dessen Abschätzung ist die Pailhes-Methode, während die Guldberg-Regel einen Zusammenhang mit der kritischen Temperatur herstellt. Der Begriff Siedepunkt wird dabei häufig als Kurzform für die Normalsiedetemperatur verwendet und stellt daher im allgemeinen Sprachgebrauch meist deren Synonym dar, was jedoch den Siedepunkt auf nur ein einziges Wertepaar reduzieren würde und daher formal inkorrekt ist.
Bei einem Schnellkochtopf macht man sich beispielsweise zunutze, dass die Siedetemperatur und der Siededruck voneinander abhängen. Durch eine Druckerhöhung von meist einem Bar (1000 hPa) erreicht man auf diese Weise eine Steigerung der Siedetemperatur des Wassers von 100 °C auf ungefähr 120 °C. Beide Temperaturen stellen Siedetemperaturen dar, jedoch ist nur der Wert von 100 °C auch die Siedetemperatur unter Normaldruck und somit die Normalsiedetemperatur. Eine Vermischung beider Begriffe ist daher unspezifisch, keineswegs selbstverständlich und sollte vermieden werden.
Siedevorgang
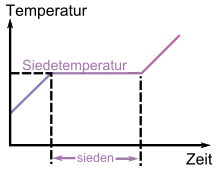
Unterhalb und oberhalb des Siedepunktes führt eine Erwärmung der Flüssigkeit bzw. des Gases nur zu einer Erhöhung der Temperatur. Die zugeführte Energie wird in Bewegungsenergie der Teilchen umgewandelt. Während des Phasenübergangs der Flüssigkeit zum Gas jedoch bleibt die Temperatur konstant, sofern auch der Druck konstant bleibt. Sämtliche zugeführte thermische Energie wird in die Zustandsänderung investiert.
Ist der Siedepunkt erreicht, so werden bei weiterer Zufuhr von Energie die chemisch-physikalischen Wechselwirkungen zwischen den Teilchen gelöst – die Teilchen treten in die Gasphase über. Die Temperatur der Flüssigkeit stagniert, da die zugeführte thermische Energie vollständig für die Lösung der zwischenmolekularen Bindungen eingesetzt wird. Die Energie, die für ein Mol des Stoffes benötigt wird, bezeichnet man auch als molare Verdampfungsenthalpie, und die nicht stoffmengenbezogene Energie als Verdampfungsenthalpie. Erst wenn alle Teilchen in der Gasphase sind, steigt die Temperatur des Systems wieder an.
Wasser, Wasserstoffperoxid oder Laugen (zum Beispiel Natronlauge) ohne Staubpartikel oder Gasbläschen lassen sich in reinen Gefäßen auch über die Siedetemperatur hinaus erwärmen, ohne dass es zum Sieden kommt. Kleinste Störungen, wie zum Beispiel Erschütterungen, die eine Durchmischung nach sich ziehen, können zu einer explosionsartigen Trennung der flüssigen von der Dampfphase führen, was man als Siedeverzug bezeichnet. Zu dessen Vermeidung fügt man bei chemischen Arbeiten Flüssigkeiten, die zu einem Siedeverzug neigen, sogenannte Siedesteinchen aus Ton oder Bimsstein hinzu, die durch die Chemikalie nicht angegriffen werden, aber durch ihre poröse Struktur die Bildung kleiner Blasen erleichtern, sodass es nicht zum Siedeverzug kommt.
Siehe auch: Verdunstung, Vergasen, Evaporation, Transpiration, Pictet-Trouton-Regel
Siedepunktskurve
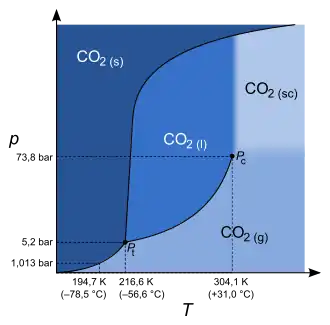
Alle Temperatur-Druck-Wertepaare an der Phasengrenzlinie Gas-Flüssigkeit in einem Phasendiagramm ergeben zusammengenommen die Siedepunktskurve, wobei auf ihr ein thermodynamisches Gleichgewicht herrscht. Man bezeichnet die Siedepunktskurve hierbei häufig auch als Siedekurve, Siedelinie, Siededruckkurve oder Siedepunktkurve. Diese Kurve wird dabei von zwei Punkten begrenzt:
- Tripelpunkt Pt: Ist das Druck-Temperatur-Wertepaar niedriger als die Tripel-Temperatur beziehungsweise der Tripel-Druck, so ist nur noch ein Übergang zwischen festem und gasförmigem Zustand, also eine Sublimation bzw. Resublimation möglich.
- Kritischer Punkt Pc: Ist das Druck-Temperatur-Wertepaar höher als die kritische Temperatur beziehungsweise der kritische Druck, so besteht zwischen der Dichte des flüssigen und der des gasförmigen Zustands kein Unterschied mehr, weshalb man sie auch nicht mehr durch eine Phasengrenzlinie trennt und den Stoff daher in diesem Zustand als überkritisches Fluid bezeichnet.
Das Gleichgewicht der Siedepunktskurve ist ein dynamisches Gleichgewicht. Aus einer Flüssigkeit treten beständig Teilchen in die Gasphase über – sie verdampfen. Andererseits treten diese Teilchen auch wieder in die flüssige Phase ein – sie kondensieren. Das Zahlenverhältnis der aus der flüssigen Phase austretenden Teilchen und der wieder in sie eintretenden Teilchen ist hierbei sowohl von der Temperatur als auch vom Druck abhängig: Je höher die Temperatur ist, desto mehr Teilchen verdampfen aufgrund ihrer höheren Geschwindigkeit (siehe Maxwell-Boltzmann-Verteilung). Je mehr Teilchen verdampfen, desto höher wird aber auch der Dampfdruck, und desto mehr Teilchen kondensieren auch wieder. Ein Gleichgewicht stellt sich dann ein, wenn genauso viel Teilchen in die Gasphase übertreten, wie wieder in die flüssige Phase zurücktreten. Da in diesem Zustand die Gasphase gesättigt ist, spricht man dann auch vom Sättigungsdampfdruck. Die thermodynamische Gesetzmäßigkeit, aus der sich die Siedepunktskurve quantitativ ableitet, bezeichnet man als Clausius-Clapeyron-Gleichung. Für Wasser lässt sich dieser Zusammenhang zwischen Sättigungsdampfdruck und Sättigungstemperatur auch über die Näherungsgleichungen vom Typ der Magnus-Formel bestimmen.
Gleichgewichtsänderung am Beispiel des Wassers
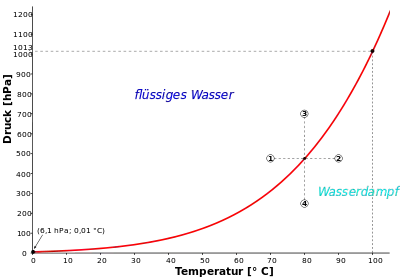
Beispielhafter Ausgangspunkt: Wasser befindet sich im Gleichgewicht mit seiner Gasphase beim Siedepunkt 80 °C und einem Druck von 474 hPa:
Die Reaktionen des Systems auf die Änderungen einzelner Zustandsgrößen laufen auf eine Verschiebung der Gleichgewichtslage hinaus: Es läuft derjenige Phasenübergang verstärkt ab, der die Störung wieder rückgängig macht (siehe Prinzip vom kleinsten Zwang).
- Wird das System auf 70 °C abgekühlt, so ist der Dampfdruck der Gasphase zu hoch, und Wasserdampf kondensiert so lange, bis der Dampfdruck den neuen Gleichgewichtswert von 312 hPa aufweist oder kein gasförmiges Wasser mehr übrig ist.
- Wird das System auf 90 °C erwärmt, so ist der Dampfdruck der Gasphase zu niedrig, und Wasser verdampft so lange, bis der Dampfdruck den neuen Gleichgewichtswert von 702 hPa aufweist oder kein flüssiges Wasser mehr übrig ist.
- Wird der Druck bei gleichbleibender Temperatur von 474 auf 700 hPa erhöht, so ist der Dampfdruck der Gasphase zu hoch, und gasförmiges Wasser kondensiert so lange, bis der Dampfdruck den alten Gleichgewichtswert von 474 hPa aufweist oder kein Wasserdampf mehr übrig ist.
- Wird der Druck bei gleichbleibender Temperatur von 474 auf 250 hPa erniedrigt, so ist der Dampfdruck der Gasphase zu niedrig, und Wasser verdampft so lange, bis der Dampfdruck den alten Gleichgewichtswert von 474 hPa aufweist oder kein flüssiges Wasser mehr übrig ist.
Stoffabhängigkeit des Siedepunktes
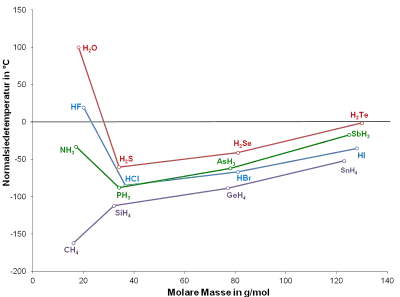
- Der Siedepunkt ist von der Stärke der Bindungskräfte zwischen den kleinsten Teilchen der flüssigen Phase abhängig: Je stärker die Bindungskräfte sind, desto höher ist der Siedepunkt, da diese zunächst überwunden werden müssten. Dies wird deutlich, wenn man beispielsweise HF und HCl vergleicht: Im flüssigen Fluorwasserstoff (Siedepunkt 20 °C) bilden die Moleküle Wasserstoffbrückenbindungen aus, während im flüssigen Chlorwasserstoff (Siedepunkt −85 °C) die schwächeren Dipol-Dipol-Wechselwirkungen vorherrschen. Gleiches gilt für den vergleichsweise sehr hohen Siedepunkt des Wassers, was deutlich wird, wenn man diesen mit Kohlenstoffdioxid vergleicht und den Einfluss der Molmassen mitberücksichtigt.
- Eine Abhängigkeit des Siedepunktes von der molaren Masse bzw. Molekülmasse des Stoffes spielt allenfalls eine untergeordnete Rolle. Häufig korrelieren größere die molare Massen mit höheren Siedepunkten, etwa aufgrund des damit verbundenen Volumen. Die molare Masse hat jedoch, anders als häufig behauptet, keinen direkten Einfluss auf die kinetische Energie,[3] welche benötigt wird, um die zwischenmolekularen Anziehungskräfte zu überwinden.[4] Ein direkter Einfluss der molaren Masse auf die zwischenmolekularen Anziehungskräfte lässt sich schwer widerlegen, da andere Einflussfaktoren schwer ausgeschlossen werden können. Empirische Ergebnisse legen einen geringfügigen Einfluss nahe.[5]
- Als vereinfachter Anhaltspunkt, um den Siedepunkt einzuschätzen, wird es dennoch verwendet. So wird die Beobachtung, dass Stoffe einen höheren Siedepunkt haben als ähnliche Stoffe mit höherer molaren Masse, als Siedepunktanomalie bezeichnet.
- Noch schwächer als Dipol-Dipol-Wechselwirkungen sind Londonsche Dispersionswechselwirkungen. Aus diesem Grund haben beim Vergleich alle Wasserstoffverbindungen der Elemente der IV. Hauptgruppe die niedrigsten Siedepunkte.
- Die Stärke der zwischenmolekularen Bindungskräfte hängt auch von der Geometrie der Moleküle ab. Siehe dazu die Siedepunkte der Homologen Reihe der Kohlenwasserstoffe oder der Alkohole.
Beispiele für Normalsiedepunkte von Reinstoffen
Chemische Elemente
- Die niedrigste Normalsiedetemperatur aller Elemente mit −269 °C hat Helium, obwohl es eine größere molare Masse als Wasserstoff mit einer Normalsiedetemperatur von −253 °C hat. Dies liegt darin begründet, dass das Wasserstoffmolekül etwas leichter zu polarisieren ist als Helium und daher auch etwas stärkere Van-der-Waals-Wechselwirkungen ausbildet.
- Die höchste Normalsiedetemperatur wird in der Literatur uneinheitlich angegeben. Wolfram und Rhenium liegen beide über 5000 °C.
- Ein Gruppenvergleich von Edelgasen, Nichtmetallen, Halbmetallen und Metallen zeigt, dass Metalle einen deutlich höheren Siedepunkt als Nichtmetalle haben, da die Metallbindung (neben der Ionen- und Atombindung) die stärkste Bindung darstellt. Ausnahmen:
- Quecksilber hat mit 357 °C eine für Metalle ungewöhnlich niedrige Normalsiedetemperatur
- Kohlenstoff weist einen für Nichtmetalle extrem hohen Siedepunkt von 4827 °C auf.
| Siedepunkte | ||||
|---|---|---|---|---|
| Minimum | Maximum | Durchschnitt | Grafische Veranschaulichung | |
| Edelgase | −269 | −62 | −170,5 | 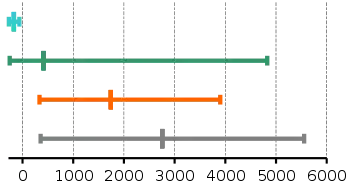 Normalsiedetemperaturen in °C von Edelgasen, Nichtmetallen, Halbmetallen und Metallen (von oben nach unten) – Minimum, Durchschnitt, Maximum |
| Nichtmetalle | −253 | 4827 | 414,1 | |
| Halbmetalle | 335 | 3900 | 1741,5 | |
| Metalle | 357 | >5000 | 2755,9 | |
Verbindungen
Eine der niedrigsten Normalsiedetemperaturen hat Kohlenstoffmonoxid mit −191,6 °C, die höchsten weisen Metallcarbide wie Titan(IV)-carbid (TiC, 4820 °C) und Wolfram(IV)-carbid (WC, 6000 °C) auf.
Eine Besonderheit liegt bei Schwefeltrioxid (SO3) vor: Der Schmelzpunkt einer seiner Modifikationen liegt mit 62,3 °C über der Normalsiedetemperatur von 44,8 °C des flüssigen Schwefeltrioxids.
Liegt der kritische Druck unter dem Normaldruck, so kann keine Normalsiedetemperatur angegeben werden. Um die Flüssigkeit dennoch zum Sieden zu bringen, muss dies unter niedrigerem Druck geschehen. In diesem Fall muss bei der Angabe der Siedetemperatur auch der Siededruck angegeben werden, was ein weiterer Grund dafür ist, die Begriffe Normalsiedetemperatur und Siedepunkt strikt zu trennen.
Liegt der Druck des Tripelpunktes über dem Normaldruck, so wird statt der Normalsiedetemperatur die Normalsublimationstemperatur oder eine Siedetemperatur bei höherem Siededruck angegeben. Beispiel: Schwefelhexafluorid SF6 sublimiert unter Normaldruck bei −63 °C.
Viele, vor allem organische und alle makromolekularen Verbindungen zersetzen sich beim Erhitzen vor Erreichen des Siedepunktes, da ihre Verdampfungsenthalpie größer ist als die einzelnen Bindungsenergien im Molekül. Hier kann man keine Siedetemperatur, sondern nur die Zersetzungstemperatur angeben. Manche können allerdings unter vermindertem Druck und bei damit niedrigerer Temperatur zum Sieden gebracht werden.
Homogene Mehrstoffsysteme
Die Siedepunkte homogener Gemische wie Legierungen, Gasgemische oder wässrige Lösungen weisen gegenüber den Reinstoffen veränderte Siedepunkte und ein verändertes Siedeverhalten auf.
Siedepunkterhöhung
Wird in einem Lösungsmittel ein Stoff gelöst, dann erhöht sich der Siedepunkt des Gemisches im Vergleich zum reinen Lösungsmittel; man spricht in Bezug auf den Sättigungsdampfdruck vom Lösungseffekt. Nach dem Raoultschen Gesetz von François Marie Raoult (1830–1901) ist diese Erhöhung ΔTSdp proportional zur Stoffmenge des gelösten Stoffes:
| Lösungsmittel | ebullioskopische Konstante in K · kg/mol[6] |
|---|---|
| Wasser | 0,513 |
| Methanol | 0,86 |
| Ethanol | 1,23 |
| Phenol | 3,54 |
| Essigsäure | 3,22 |
| Benzol | 2,64 |
| Schwefelkohlenstoff | 2,42 |
| Kohlenstofftetrachlorid | 5,26 |
| Cyclohexan | 2,92 |
Hierbei stehen die einzelnen Formelzeichen für folgende Größen:
- ΔTSdp - Siedepunktserhöhung
- Ke - ebullioskopische Konstante
- b - Molalität des gelösten Stoffes
- K - molare Siedepunktserhöhung
- n - Stoffmenge
Der Proportionalitätsfaktor ist, wie dargelegt, die ebullioskopische Konstante (auch Siedepunktskonstante KS), also die Änderung des Siedepunktes von einem Kilogramm der Lösung gegenüber dem reinen Lösungsmittel, wobei die Stoffmenge des gelösten Stoffes ein Mol beträgt oder die molare Siedepunktserhöhung, die weniger gebräuchlich ist und keine Aussage zur Masse trifft.
So steigt beispielsweise der Siedepunkt eines Kilogramms Wasser um 0,51 K auf 100,51 °C, wenn man genau ein Mol irgendeines anderen Stoffes darin auflöst, vorausgesetzt, der Stoff löst sich in Wasser und ist nicht flüchtig. Löst man zwei Mol in einem Kilogramm Wasser auf, so siedet das Wasser erst bei 100 °C + 2 × 0,51 °C = 101,02 °C.
Es ist dabei zu beachten, dass Salze in wässriger Lösung dissoziieren. Natriumchlorid zerfällt zum Beispiel in die Ionen Na+ und Cl−. Die Siedepunkterhöhung ist daher (in verdünnten Lösungen) doppelt so hoch wie zunächst erwartet.
Ein praktisches Beispiel: Nudelwasser hat einen typischen Kochsalzgehalt von 10 g/kg. Bei einer Molmasse von 58,4 g/mol entspricht dies, zusammen mit oben erwähnter Verdopplung, 0,34 mol/kg Ionen. Durch den Salzgehalt ergibt sich also eine Siedepunkterhöhung von nur etwa 0,17 K.
Das Raoultsche Gesetz gilt nur für „ideale“ Lösungen, das sind Lösungen, bei denen ein Stoff nur physikalisch gelöst wird. Bei „nichtidealen“ Lösungen treten während des Mischens energetische Erscheinungen (Erwärmung oder Abkühlung) auf, die in der Ausbildung von Wasserstoffbrückenbindungen oder durch Protolysen hervorgerufen werden. Dadurch ergeben sich Abweichungen vom Raoultschen Gesetz. Nur in sehr starker Verdünnung gilt die Formel auch bei „nichtidealen“ Lösungen in Annäherung, weshalb man im Falle der idealen Lösung auch von einer unendlich verdünnten Lösung spricht. Die Siedepunktserhöhung ist zudem eine kolligative Eigenschaft und hängt daher zwar von der Teilchenzahl des gelösten Stoffes, nicht jedoch von dessen Art ab. Über eine Umstellung der obigen Formel kann die Siedepunktserhöhung auch zur Molmassebestimmung dienen, was man als Ebullioskopie bezeichnet.
Ebenso von der Konzentration der gelösten Stoffe abhängig ist der Schmelzpunkt, weshalb man auch von einer Schmelzpunkterniedrigung spricht. Ursache für diese Effekte ist ebenfalls eine Erniedrigung des chemischen Potentials. Kombiniert man Siedepunkterhöhung und Schmelzpunkterniedrigung, so zeigt sich insgesamt eine Ausdehnung des thermodynamischen Zustandsbereiches der Flüssigkeit zu Lasten der anderen Aggregatzustände.
Zeotrope Gemische
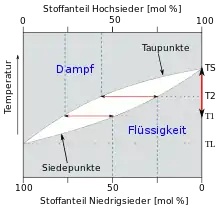
TL Siedetemp. des Leichtsieders
TS Siedetemp. des Schwersieders
Rechts rot markiert: Siedebereich einer 50 %-Mischung zwischen T1 und TS
Wird eine zeotrope Mischung zweier Flüssigkeiten erhitzt, so beginnt sie bei einer Temperatur oberhalb der Siedetemperatur des Leichtsieders, also desjenigen Bestandteils mit der niedrigeren Siedetemperatur, zu sieden. Beim Sieden gehen gleichzeitig beide Bestandteile in die Gasphase über. Dabei hat der Leichtsieder im austretenden Dampf eine höhere Konzentration, als seiner Konzentration im flüssigen Gemisch entspricht. Deshalb reichert sich in der Flüssigkeit der Schwersieder an und die Siedetemperatur steigt kontinuierlich bis zum Siedepunkt des Schwersieders. Man spricht in diesem Fall von einem Siedebereich (auch Siedeintervall, Siedegrenze) des Gemisches und nicht mehr von einem Siedepunkt.[7]
Die Abhängigkeit der Siedetemperatur von dem Verhältnis der flüssigen Bestandteile und das jeweils zugehörige Verhältnis im verdampfenden Gas werden im Siedediagramm (rechts) dargestellt. Der freie Bereich in der Mitte, in dem weder Gas noch Flüssigkeit existieren können, wird wegen seiner Form Siedelinse genannt. Am rechten Rand ist der Siedebereich einer Lösung mit 50 % Stoffmengenanteil markiert.
Dieses Verhalten wird technisch genutzt, um Konzentrationen von Einzelkomponenten in Gemischen durch Destillation oder Rektifikation zu erhöhen.
Azeotrope Gemische

Sdp. 1: Siedepunkt der Reinstoffkomponente 1, Sdp. 2: Siedepunkt der Reinstoffkomponente 2, x: Stoffmengenanteil von Komponente 2 im azeotropen Gemisch
Bei azeotropen Stoffgemischen hat die Siedetemperatur des Stoffgemisches bei einem bestimmten Stoffmengenverhältnis einen Extremwert. Dieser Wert liegt außerhalb des Temperaturintervalles, das durch die Siedetemperaturen der beiden Reinstoffe aufgespannt wird. Bei diesem besonderen Mischungsverhältnis liegt ein Siedepunkt und kein Siedebereich vor.
Beispiele:
Bedeutung für die Lebewesen
Das Siedeverhalten des Wassers führt unter den physikalischen Bedingungen auf der Erde dazu, dass Wasser in großen Mengen als Flüssigkeit existiert. Dies ist eine der grundlegenden Voraussetzungen für die Entwicklung von Lebewesen.
Bei einem niedrigeren Luftdruck oder höheren Temperaturen des Wassers wäre dies anders und würde dazu führen, dass Gewässer binnen kürzester Zeit verdampfen und somit auch eine wichtige Bedingung für das Leben überhaupt, nämlich flüssiges Wasser, wesentlich seltener anzutreffen wäre. Bei einem höheren Luftdruck bzw. einer niedrigeren Temperatur würde jedoch immer weniger Wasser verdunsten können, und somit würde die Voraussetzung für Niederschläge, nämlich gasförmiges Wasser in der Atmosphäre, immer seltener, was beispielsweise eine Einschränkung der Süßwasservorkommen nach sich ziehen würde.
Anwendungen
- Analytische Chemie: Der Siedepunkt ist eine spezifische Stoffeigenschaft. Somit lassen sich Reinstoffe anhand ihres Siedepunktes charakterisieren.
- Destillation bzw. fraktionierte Destillation, eine Methode zur Trennung eines Stoffgemisches aufgrund unterschiedlicher Siedepunkte der Einzelkomponenten. Der niedersiedende Stoff wird vom höhersiedenden Stoff durch Verdampfen abgetrennt.
- Die Ebullioskopie (lat. bulla = Siedeblase, gr. skopein = betrachten) ist eine Methode zur Bestimmung der molaren Massen durch Siedepunktserhöhung. Da Siedepunktserhöhungen kleiner ausfallen als Gefrierpunktserniedrigungen, wird in der Regel die Kryoskopie bevorzugt. Bei beiden Methoden findet ein spezielles Thermometer seine Anwendung, das 1888 von Ernst Otto Beckmann (1853–1923) entwickelt wurde: das Beckmann-Thermometer. Es hat eine Skala, die nur ungefähr 6° umfasst, kann jedoch auch auf 0,01 Grad genau abgelesen werden. Der Nullpunkt der Skala kann auf die jeweils gewünschte Temperatur eingestellt werden.
- Schnellkochtopf: Wird Wasser in einem luftdicht verschlossenen Topf erhitzt, kann die Temperatur des flüssigen Wassers über 100 °C steigen, weil der Siededruck und damit auch der Siedepunkt sich erhöhen. Dadurch kommt es zu einer schnelleren Garung.
- Höhenmessung: Da der Luftdruck mit zunehmender Höhe sinkt, sinkt auch der Siedepunkt. Als Faustregel gilt: Der Siedepunkt wird pro 300 m um etwa ein Grad abgesenkt. So lässt sich durch die Bestimmung der Siedetemperatur von reinem Wasser die jeweilige Höhe über dem mittleren Meeresspiegel abschätzen.
Bestimmung der Siedepunkte von organischen Stoffen
Der Siedepunkt ist eine Stoffeigenschaft. Die Kenntnis des Siedepunktes ermöglicht Rückschlüsse auf den vorliegenden Stoff. In Nachschlagewerken (z. B. CRC Handbook of Chemistry and Physics oder Taschenbuch für Chemiker und Physiker) befinden sich Tabellen über Siedepunkte von Stoffen und Stoffgemischen. Aus den Tabellenwerten kann man die vermuteten Verbindungen häufig abschätzen.
Der Siedepunkt kann auch als ein Kriterium der Stoffreinheit eines bekannten Stoffes genutzt werden. Für destillative Stofftrennungen eignet sich eine Vigreuxkolonne.
Bei Stoffmischungen kann es auch vorkommen, dass mehrere Stoffe bei dem gleichen Siedepunkt überdestillieren, das Stoffgemisch bildet dann ein Azeotrop.
Bestimmung des Siedepunktes mit einfachen Mitteln
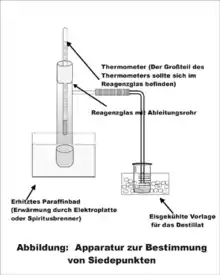
Für einfache Ermittlungen der Siedetemperatur benötigt man ein Reagenzglas (oder einen Kolben) mit einem seitlichen Ansatzrohr mit durchbohrtem Gummistopfen und Thermometer, ein Stück Gummischlauch, ein Glasrohr, ein Paraffinbad, eine Heizquelle und ein Becherglas mit Kühlwanne. Entsprechend der Abbildung Apparatur zur Bestimmung des Siedepunktes wird die eine entsprechende Destillationsvorrichtung aufgebaut.
Das Reagenzglas mit Ansatzrohr sollte zu einem Drittel mit dem zu untersuchenden Stoff gefüllt werden. Zur Verhinderung von Siedeverzügen fügt man noch einige Siedesteinchen hinzu. Die untere Spitze des Thermometers sollte wenige Zentimeter über der Flüssigkeitsoberfläche angebracht sein. Für eine genauere Temperaturermittlung kann statt eines Quecksilberthermometers auch ein digitaler Temperaturfühler (Genauigkeit: 0,1 °C) durch den Gummistopfen eingebracht werden.
Für eine sehr exakte Bestimmung des Siedepunktes müssen zwei mögliche Fehlerquellen beachtet werden:
- Falls ein Quecksilberthermometer zur Bestimmung des Siedepunktes genutzt wird, muss das Thermometer sehr weit in das Reagenzglas hineinragen. Durch die deutlich kühlere Umgebungsluft wird das Quecksilber, das sich nicht im Innenraum der Dampfzone befindet, abgekühlt. Der dabei entstehende Temperaturfehler wird annähernd durch die Formel ΔT = 0,000154·n·(T - t) beschrieben. (n = Länge (cm) des herausragenden Teilstückes, T = beobachtete Siedetemperatur, t = Temperatur der Umgebungsluft).[8]
- Falls der Luftdruck von 760 mm Quecksilbersäule abweicht, so muss ein weiterer Korrekturfaktor des Siedepunktes berücksichtigt werden. Überschlägig führt eine Druckabweichung von 0,36 % (2,4 mm Quecksilbersäule) zum Normaldruck zu einer Siedepunktabweichung von mindestens 0,1 °C.[9]
Einzelnachweise
- ChemgaPedia: Glossar: Siedepunkt.
- Pure Appl. Chem., Vol. 54, No. 6, S. 1239–1250, 1982. Volltext (PDF-Datei; 227 kB).
- Erwin Riedel: Allgemeine und Anorganische Chemie. 10. Auflage. De gruyter Studium, Berlin / New York 2010, ISBN 978-3-11-022781-9, S. 144.
- Hans Peter Latscha, Helmut Alfons Klein, Martin Mutz: Allgemeine Chemie (= Springer-Lehrbuch). Springer Berlin Heidelberg, Berlin, Heidelberg 2011, ISBN 978-3-642-17522-0, S. 168, doi:10.1007/978-3-642-17523-7 (springer.com [abgerufen am 30. April 2021]).
- Michael Laing: Boiling Points of the Family of Small Molecules, CHwFxClyBrz: How Are They Related to Molecular Mass? In: Journal of Chemical Education. Band 78, Nr. 11, 2001, ISSN 0021-9584, S. 1544, doi:10.1021/ed078p1544 (acs.org [abgerufen am 30. April 2021]).
- David R. Lide (Hrsg.): CRC Handbook of Chemistry and Physics. 90. Auflage. (Internet-Version: 2010), CRC Press/Taylor and Francis, Boca Raton, FL, Ebullioscopic Constants for Calculation of Boiling Point Elevation, S. 15-27.
- S. Scholl, Henning Föste: Verfahrenstechnisches Labor. Rektifikation. (PDF; 2,1 MB [abgerufen am 9. November 2013]).
- Ber. d. Deut. Chem. Ges. 22, 3072.
- Ber. d. Deut. Chem. Ges. 20, 709.