Höhenmessung
Die Höhenmessung ist ein Teilgebiet der Geodäsie, teilweise auch der Geografie (Topografie) und der Maschinen- bzw. Bautechnik. Höhen werden in vielfältigen Bereichen benötigt und bestimmt, z. B. in der Ingenieur- und Landesvermessung, in Geologie und Raumplanung, im Maschinen- und Bauwesen, beim Bergsteigen oder in der Navigation.
Vereinzelt spricht man statt von Höhenmessung auch von Altimetrie – insbesondere bei Übersetzungen aus dem Englischen, bei Altimeter-Instrumenten und bei der Satellitenaltimetrie.
Abgrenzungen
Höhenmessungen können sehr unterschiedliche Bezugsflächen haben, was bei Datenvergleichen zu beachten ist – siehe Höhe (Geodäsie):
- „Relative Höhen“ sind ein Maß, um wie viel ein Objekt die Umgebung überragt (wichtig z. B. im Bauwesen, in der Luftfahrt, beim Bergsport und für das Berechnen des Energieaufwandes).
- „Absolute Höhen“ sind physikalisch und beziehen sich auf das Erdschwerefeld und daher als Horizontbezug praxishalber auf den mittleren Meeresspiegel (Geoid). Die staatlichen Höhennetze sind allerdings durch unterschiedliche Pegel definiert und nicht einheitlich bearbeitet, was zu Unterschieden im cm- bis dm-Bereich führen kann.
- „Höhen aus Satellitenmessungen“ sind rein geometrisch und beziehen sich auf ein mathematisches Erdellipsoid (heute meist WGS84-System). Der Unterschied zu Meereshöhen kann 100 Meter erreichen (in Mitteleuropa ca. 50 m, siehe Geoid). Wegen der geometrischen Natur dieser Messungen kann „zwischen Punkten gleicher GPS-Höhe Wasser fließen“ (W. Torge 1999), sodass sie für Vermessungszwecke eine Korrektur benötigen.
Methoden der Höhenmessung
Die Höhenmessung selbst kann auf sehr verschiedene Arten erfolgen:
- nivellitisch (bezüglich einer Niveaufläche der Erde):
- durch Messung geometrischer Höhenunterschiede mit dem Nivelliergerät
- durch Messung physikalischer Höhenunterschiede mit der Schlauchwaage
- trigonometrisch – durch Messung von Höhenwinkeln und schräger Strecken (siehe trigonometrisches Nivellement, Tachymetrie und Instrumentenhöhe)
- mittels GPS- oder GNSS-Satelliten (siehe ellipsoidische Höhe und GPS-Leveling)
- durch Laufzeitmessung von Schallwellen in Wasser, etwa beim Echolot
- durch Laufzeitmessung von Mikrowellen beim Dauerstrichradar
- barometrisch – durch Messung von Luftdruckdifferenzen mit einem Aneroid-Barometer (Hypsometer)
- barometrische Höhenmessung in der Geodäsie
- Höhenmesser für Kartografie und Wandern
- barometrische Höhenmessung in der Luftfahrt, Aufzeichnung der Höhen mit Höhenschreiber
- gravimetrisch – mit einem Gravimeter (→ dynamische Höhe)
- fotogrammetrisch – durch Auswertung von Stereobildpaaren aus der Luft
- mittels Fernerkundung, z. B. durch Laufzeitmessung von Laser- oder Radarwellen (→ Radarinterferometrie)
- aus der Luft (→ Laserscanner)
- aus dem Weltraum (→ Satellitenaltimetrie, Lasermethoden der Satellitengeodäsie, SRTM-Radar).
Spezielle Messmethoden und Höhenmarken
Darüber hinaus sind spezielle Messmethoden in Maschinenbau und Labortechnik zu erwähnen, etwa bei der Justierung von Maschinenachsen oder bei Füllstandsmessungen von Flüssigkeiten. Die Geodäsie kennt ferner das astronomische Nivellement zur genauen Analyse des Erdschwerefeldes (siehe Geoidbestimmung) und die Messung von Raumpolygonen, bei der Lage- und Höhenmessung kombiniert werden.
Die Genauigkeit reicht von hundertstel Millimetern beim Präzisionsnivellement über Millimeter bei trigonometrischer Höhenmessung und Zentimeter bei GPS bis zum Dezimeter bzw. einigen Metern bei Satellitenaltimetrie und barometrischer Höhenmessung. Die Festpunkte des Präzisionsnivellements müssen wegen ihrer hohen Genauigkeit besonders stabil vermarkt werden, da sie nicht nur die Basis aller technischen Nivellements ist, sondern auch für die vertikalen Erdkrustenbewegungen, die je nach Geologie des Untergrunds 0,01 mm bis einige Millimeter pro Jahr betragen. Die Höhenmarken werden daher sorgfältig in alte Gebäude eingemauert, die keiner Setzung mehr unterliegen, wie Kirchen (siehe Turmbolzen) und Amtsgebäude (siehe Bild), bzw. in gewachsenem Fels oder an tief reichenden Fundamenten angebracht.
Die strenge Definition von „Höhe“ ist ein mehrschichtiges Problem, weil sie auf verschiedene Weise erfolgen kann, z. B. rein geometrisch oder gravimetrisch-physikalisch. Damit befasste Fachgebiete sind die Höhere Geodäsie, die Geometrie und die Potentialtheorie.
Relative Höhenmessungen mit geringem Aufwand
- Nicht immer kann größerer Aufwand (Geräte und/oder Rechenoperationen) betrieben werden, um die Höhe eines Objektes zu ermitteln.
- Die erreichbaren Genauigkeiten sind dadurch begrenzt, reichen aber für sehr viele Anwendungen aus (z. B. Baumhöhenmessungen).
- Die gängigen Methoden beruhen auf Winkelmessungen mit einem Klinometer und einem gleichschenklig-rechtwinkligen Dreieck.
- Ebenfalls auf Winkelmessungen beruht die Anwendung des Spiegelhypsometers.
- Ein nicht auf direkten Winkelmessungen beruhendes Verfahren wird Höhenmessung mit dem Försterstäbchen genannt, welches zur Messung stets eine Hilfsperson benötigt und in der Regel auf Baumhöhenmessungen beschränkt ist.
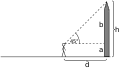Bestimmung der Turmhöhe mit einem gleichseitigen Dreieck,
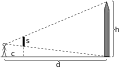… mit dem Strahlensatz oder
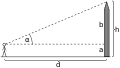… mit Trigonometrie.
Gemäß dem mathematischen Grundsatz, dass zur Berechnung einer unbekannten Größe in einem Dreieck stets zwei weitere Größen erforderlich sind, werden bei der Höhenmessung die Größen Abstand zum Messobjekt („Basislinie“) und der „Höhenwinkel“ (Winkel, unter dem der höchste zu messende Punkt am Ende der Basislinie zu sehen ist) zur Berechnung herangezogen.
Wird ein Klinometer mit Gradeinteilung verwendet, ergibt sich die Höhe des Objektes nach der Tangens-Beziehung (Winkelfunktion):
- Basislinie (d) × tan Höhenwinkel (α) = Objekthöhe
oder:
- sin Höhenwinkel x Sperrmaß (Schrägdistanz) zum Hochpunkt = Objekthöhe
Eine Tabelle oder geeigneter Taschenrechner/Rechenstab wird benötigt.
Auf einen Taschenrechner/Rechenstab oder eine Tabelle kann verzichtet werden, wenn sich der Beobachter dem Objekt dergestalt nähert, dass er den höchsten Punkt unter einem Winkel von 30° (Klinometer!) sieht. In diesem Fall ist die Objekthöhe = Höhensperrmaß/2 (der sin 30° beträgt 0,5)
Wird ein Klinometer mit %-Skala verwendet, ergibt sich die Höhe des Objektes nach der Formel:
- %-Wert/100 × Basislinie (d)
Die Messung mit dem Dreieck beruht auf der Tatsache, dass der Tangens eines Winkel von 45° = 1 ist. Daraus folgt, dass die Höhe des Objektes gleich der Basislinie ist, wenn die höchste Stelle des Objektes unter einem Winkel von 45° gesehen wird. Dies ist der Fall, wenn über die Hypotenuse des Dreieckes (das aus Papier gefaltet werden kann) das Objekt eingepeilt wird (dabei muss die zu Boden weisende Kathete des Dreieckes waagerecht gehalten werden).
Da die beschriebenen Messungen über dem Boden (aus „Augenhöhe“) ermittelt werden, ist diese Höhe dem Ergebnis hinzuzuzählen (z. B. 1,70 m).
Siehe auch
Literatur
- Wolfgang Torge: Geodesy. 3rd, completely revised and extended edition. de Gruyter, Berlin u. a. 2001, ISBN 3-11-017072-8.
- Heribert Kahmen: Vermessungskunde. 18., völlig neu bearbeitete und erweiterte Auflage. de Gruyter, Berlin u. a. 1993, ISBN 3-11-013733-X.