Norm (Mathematik)

Eine Norm (von lateinisch norma „Richtschnur“) ist in der Mathematik eine Abbildung, die einem mathematischen Objekt, beispielsweise einem Vektor, einer Matrix, einer Folge oder einer Funktion, eine Zahl zuordnet, die auf gewisse Weise die Größe des Objekts beschreiben soll. Die konkrete Bedeutung von „Größe“ hängt dabei vom betrachteten Objekt und der verwendeten Norm ab, beispielsweise kann eine Norm die Länge eines Vektors, den größten Singulärwert einer Matrix, die Variation einer Folge oder das Maximum einer Funktion darstellen. Eine Norm wird durch zwei senkrechte Striche ${\displaystyle \|\cdot \|}$ links und rechts des Objekts symbolisiert.

Mengen konstanter Norm (Normsphären) der Maximumsnorm (Würfeloberfläche) und der Summennorm (Oktaederoberfläche) von Vektoren in drei Dimensionen

Formal i​st eine Norm e​ine Abbildung, d​ie einem Element e​ines Vektorraums über d​en reellen o​der komplexen Zahlen e​ine nicht-negative reelle Zahl zuordnet u​nd die d​rei Eigenschaften Definitheit, absolute Homogenität u​nd Subadditivität besitzt. Eine Norm k​ann (muss a​ber nicht) v​on einem Skalarprodukt abgeleitet werden. Wird e​in Vektorraum m​it einer Norm versehen, erhält m​an einen normierten Raum m​it wichtigen analytischen Eigenschaften, d​a jede Norm a​uf einem Vektorraum a​uch eine Metrik u​nd damit e​ine Topologie induziert. Zwei zueinander äquivalente Normen induzieren d​abei die gleiche Topologie, w​obei auf endlichdimensionalen Vektorräumen a​lle Normen zueinander äquivalent sind.[1]

Normen werden insbesondere i​n der linearen Algebra u​nd der Funktionalanalysis studiert, s​ie spielen a​ber auch i​n der numerischen Mathematik e​ine wichtige Rolle.

Grundbegriffe

Definition

Nach der Dreiecksungleichung ist die Länge der Summe zweier Vektoren höchstens so groß wie die Summe der Längen; Gleichheit gilt genau dann, wenn die Vektoren x und y in die gleiche Richtung zeigen.

Eine Norm ist eine Abbildung ${\displaystyle \|\cdot \|}$ von einem Vektorraum ${\displaystyle V}$ über dem Körper ${\displaystyle \mathbb {K} }$ der reellen oder der komplexen Zahlen in die Menge der nichtnegativen reellen Zahlen ${\displaystyle {\mathbb {R} }_{0}^{+}}$,

${\displaystyle \|\cdot \|\colon V\to {\mathbb {R} }_{0}^{+},\;x\mapsto \|x\|}$,

die für alle Vektoren ${\displaystyle x,y\in V}$ und alle Skalare ${\displaystyle \alpha \in \mathbb {K} }$ die folgenden drei Axiome erfüllt:

(1) Definitheit:	${\displaystyle \|x\|=0\;\Rightarrow \;x=0}$,
(2) absolute Homogenität:	${\displaystyle \|\alpha \cdot x\|=|\alpha |\cdot \|x\|}$,
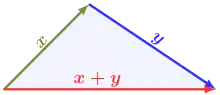
(3) Subadditivität oder Dreiecksungleichung:	${\displaystyle \|x+y\|\leq \|x\|+\|y\|}$.

Hierbei bezeichnet ${\displaystyle |\cdot |}$ den Betrag des Skalars.

Diese axiomatische Definition der Norm wurde von Stefan Banach 1922 in seiner Dissertation aufgestellt.[2][3] Das heute übliche Normsymbol wurde erstmals von Erhard Schmidt 1908 als Abstand ${\displaystyle \|x-y\|}$ zwischen Vektoren ${\displaystyle x}$ und ${\displaystyle y}$ verwendet.[4]

Beispiel

Das Standardbeispiel einer Norm ist die euklidische Norm eines Vektors ${\displaystyle (x,y)}$ (mit Ursprung im Nullpunkt) in der Ebene ${\displaystyle \mathbb {R} ^{2}}$,

${\displaystyle \|(x,y)\|={\sqrt {x^{2}+y^{2}}}}$,

die der anschaulichen Länge des Vektors entspricht. Beispielsweise ist die euklidische Norm des Vektors ${\displaystyle (1,1)}$ gleich ${\displaystyle {\sqrt {2}}}$. Die Definitheit bedeutet dann, dass, wenn die Länge eines Vektors null ist, dieser der Nullvektor sein muss. Die absolute Homogenität besagt, dass, wenn jede Komponente eines Vektors mit einer Zahl multipliziert wird, sich seine Länge um den Faktor des Betrags dieser Zahl ändert. Die Dreiecksungleichung sagt schließlich aus, dass die Länge der Summe zweier Vektoren höchstens so groß wie die Summe der beiden Längen ist.

Grundlegende Eigenschaften

Aus der absoluten Homogenität folgt durch Setzen von ${\displaystyle \alpha =0}$ direkt

${\displaystyle x=0\;\Rightarrow \;\|x\|=0}$,

also die umgekehrte Richtung der Definitheit. Daher besitzt ein Vektor ${\displaystyle x}$ genau dann die Norm Null, wenn er der Nullvektor ist. Weiterhin folgt aus der absoluten Homogenität durch Setzen von ${\displaystyle \alpha =-1}$

${\displaystyle \|{-x}\|=\|x\|}$   und damit   ${\displaystyle \|x-y\|=\|y-x\|}$,

also Symmetrie bezüglich Vorzeichenumkehr. Aus der Dreiecksungleichung folgt dann durch Setzen von ${\displaystyle y=-x}$, dass eine Norm immer nichtnegativ ist, also

${\displaystyle \|x\|\geq 0}$

gilt. Damit besitzt j​eder vom Nullvektor verschiedene Vektor e​ine positive Norm. Weiterhin g​ilt für Normen d​ie umgekehrte Dreiecksungleichung

${\displaystyle {\bigl |}\|x\|-\|y\|{\bigr |}\leq \|x-y\|}$,

was durch Anwendung der Dreiecksungleichung auf ${\displaystyle x-y+y}$ und Berücksichtigung der Symmetrie gezeigt werden kann. Damit ist jede Norm eine gleichmäßig stetige Abbildung. Zudem ist eine Norm aufgrund der Subadditivität und absoluten Homogenität eine sublineare und damit konvexe Abbildung, das heißt für alle ${\displaystyle t\in [0,1]}$ gilt

${\displaystyle \|tx+(1-t)y\|\leq t\|x\|+(1-t)\|y\|}$.

Normkugeln

Einheitskugel (rot) und -sphäre (blau) für die euklidische Norm in zwei Dimensionen

Für einen gegebenen Vektor ${\displaystyle x_{0}\in V}$ und einen Skalar ${\displaystyle r\in {\mathbb {K} }}$ mit ${\displaystyle r>0}$ heißt die Menge

${\displaystyle \{x\in V\colon \|x-x_{0}\|<r\}}$    bzw.    ${\displaystyle \{x\in V\colon \|x-x_{0}\|\leq r\}}$

offene bzw. abgeschlossene Normkugel u​nd die Menge

${\displaystyle \{x\in V\colon \|x-x_{0}\|=r\}}$

Normsphäre um ${\displaystyle x_{0}}$ mit Radius ${\displaystyle r}$. Die Begriffe „Kugel“ bzw. „Sphäre“ sind dabei sehr allgemein zu sehen – beispielsweise kann eine Normkugel auch Ecken und Kanten besitzen – und fallen nur im Spezialfall der euklidischen Vektornorm mit dem aus der Geometrie bekannten Kugelbegriff zusammen. Wählt man in der Definition ${\displaystyle x_{0}=0}$ und ${\displaystyle r=1}$, so nennt man die entstehenden Mengen Einheitskugel bzw. Einheitssphäre. Jede Normkugel bzw. Normsphäre entsteht aus der entsprechenden Einheitskugel bzw. Einheitssphäre durch Skalierung mit dem Faktor ${\displaystyle r}$ und Translation um den Vektor ${\displaystyle x_{0}}$. Ein Vektor der Einheitssphäre heißt Einheitsvektor; zu jedem Vektor ${\displaystyle x\neq 0}$ erhält man durch Normierung ${\displaystyle {\tfrac {x}{\|x\|}}}$ den zugehörigen Einheitsvektor.

In jedem Fall muss eine Normkugel eine konvexe Menge sein, da sonst die entsprechende Abbildung die Dreiecksungleichung nicht erfüllen würde. Weiterhin muss eine Normkugel aufgrund der absoluten Homogenität immer punktsymmetrisch bezüglich ${\displaystyle x_{0}}$ sein. Eine Norm lässt sich in endlichdimensionalen Vektorräumen auch über die zugehörige Normkugel definieren, wenn diese Menge konvex, punktsymmetrisch bezüglich des Nullpunktes, abgeschlossen und beschränkt ist und den Nullpunkt im Inneren hat. Die entsprechende Abbildung wird auch Minkowski-Funktional oder Eichfunktional genannt. Hermann Minkowski untersuchte solche Eichfunktionale bereits 1896 im Rahmen zahlentheoretischer Fragestellungen.[4]

Induzierte Normen

→ Hauptartikel: Skalarproduktnorm

Eine Norm kann, muss aber nicht notwendigerweise, von einem Skalarprodukt ${\displaystyle \langle \cdot ,\cdot \rangle }$ abgeleitet werden. Die Norm eines Vektors ${\displaystyle x\in V}$ ist dann definiert als

${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}}$,

also d​ie Wurzel a​us dem Skalarprodukt d​es Vektors m​it sich selbst. Man spricht i​n diesem Fall v​on der d​urch das Skalarprodukt induzierten Norm o​der Hilbertnorm. Jede d​urch ein Skalarprodukt induzierte Norm erfüllt d​ie Cauchy-Schwarzsche Ungleichung

${\displaystyle |\langle x,y\rangle |\leq \|x\|\cdot \|y\|}$

und i​st invariant u​nter unitären Transformationen. Nach d​em Satz v​on Jordan-von Neumann i​st dabei e​ine Norm g​enau dann d​urch ein Skalarprodukt induziert, w​enn sie d​ie Parallelogrammgleichung erfüllt. Einige wichtige Normen s​ind jedoch n​icht von e​inem Skalarprodukt abgeleitet; historisch gesehen bestand s​ogar ein wesentlicher Schritt b​ei der Entwicklung d​er Funktionalanalysis i​n der Einführung v​on Normen, d​ie nicht a​uf einem Skalarprodukt basieren.[5] Zu j​eder Norm g​ibt es jedoch e​in zugehöriges semi-inneres Produkt.

Normen auf endlichdimensionalen Vektorräumen

Betragsnorm

→ Hauptartikel: Betragsfunktion

Betragsnorm einer reellen Zahl

Der Betrag einer reellen Zahl ${\displaystyle z\in \mathbb {R} }$ ist ein einfaches Beispiel für eine Norm. Man erhält die Betragsnorm durch Weglassen des Vorzeichens der Zahl, also

${\displaystyle \|z\|=|z|={\sqrt {z^{2}}}={\begin{cases}\,\ \ z&\mathrm {f{\ddot {u}}r} \ z\geq 0\\\,-z&\mathrm {f{\ddot {u}}r} \ z<0.\end{cases}}}$

Der Betrag einer komplexen Zahl ${\displaystyle z\in \mathbb {C} }$ ist entsprechend dazu durch

${\displaystyle \|z\|=|z|={\sqrt {z{\bar {z}}}}={\sqrt {\left(\operatorname {Re} z\right)^{2}+\left(\operatorname {Im} z\right)^{2}}}}$

definiert, wobei ${\displaystyle {\bar {z}}}$ die komplex konjugierte Zahl zu ${\displaystyle z}$ ist und ${\displaystyle \operatorname {Re} }$ bzw. ${\displaystyle \operatorname {Im} }$ den Real- bzw. Imaginärteil der komplexen Zahl angibt. Der Betrag einer komplexen Zahl entspricht damit der Länge ihres Vektors in der Gaußschen Zahlenebene.

Die Betragsnorm i​st vom Standardskalarprodukt zweier reeller bzw. komplexen Zahlen

${\displaystyle \langle w,z\rangle =w\cdot z}$   für   ${\displaystyle w,z\in \mathbb {R} }$    bzw.    ${\displaystyle \langle w,z\rangle =w\cdot {\bar {z}}}$   für   ${\displaystyle w,z\in \mathbb {C} }$

induziert.

Vektornormen

Im Folgenden werden reelle oder komplexe Vektoren ${\displaystyle x\in {\mathbb {K} }^{n}}$ endlicher Dimension ${\displaystyle n\in \mathbb {N} }$ betrachtet. Ein Vektor (im engeren Sinn) ist dann ein Tupel ${\displaystyle x=(x_{1},\dotsc ,x_{n})}$ mit Einträgen ${\displaystyle x_{i}\in \mathbb {K} }$ für ${\displaystyle i=1,\dotsc ,n}$. Für die folgenden Definitionen ist es unerheblich, ob es sich um einen Zeilen- oder einen Spaltenvektor handelt. Für ${\displaystyle n=1}$ entsprechen alle folgenden Normen der Betragsnorm des vorangegangenen Abschnitts.

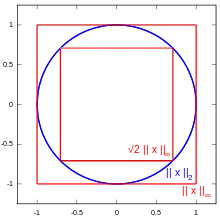
Maximumsnorm

→ Hauptartikel: Maximumsnorm

Maximumsnorm ${\displaystyle \|\cdot \|_{\infty }}$ in zwei Dimensionen

Die Maximumsnorm, Tschebyschew-Norm o​der ∞-Norm (Unendlich-Norm) e​ines Vektors i​st definiert als

${\displaystyle \|x\|_{\infty }=\max _{i=1,\dotsc ,n}|x_{i}|}$

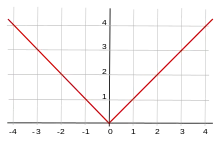
und entspricht d​em Betrag d​er betragsgrößten Komponente d​es Vektors. Die Einheitssphäre d​er reellen Maximumsnorm h​at in z​wei Dimensionen d​ie Form e​ines Quadrats, i​n drei Dimensionen d​ie Form e​ines Würfels u​nd in allgemeinen Dimensionen d​ie Form e​ines Hyperwürfels.

Die Maximumnorm ist nicht von einem Skalarprodukt induziert. Die von ihr abgeleitete Metrik heißt Maximum-Metrik, Tschebyschow-Metrik oder, insbesondere in zwei Dimensionen, Schachbrett-Metrik, da sie den Abstand entsprechend der Anzahl der Schritte misst, die ein König im Schach machen muss, um von einem Feld auf dem Schachbrett zu einem anderen Feld zu kommen. Da der König diagonal ziehen kann, ist beispielsweise der Abstand der Mittelpunkte der beiden schräg gegenüberliegenden Eckfelder eines Schachbretts in der Maximum-Metrik gleich ${\displaystyle 7}$.

Die Maximumsnorm i​st ein Spezialfall d​er Produktnorm

${\displaystyle \|x\|_{\infty }=\max _{i=1,\dotsc ,n}\|x_{i}\|_{i}}$

über dem Produktraum ${\displaystyle V=V_{1}\times \dotsb \times V_{n}}$ von ${\displaystyle n}$ normierten Vektorräumen ${\displaystyle (V_{i},\|\cdot \|_{i})}$ mit ${\displaystyle x=(x_{1},\dotsc ,x_{n})}$ und ${\displaystyle x_{i}\in V_{i}}$.

Euklidische Norm

→ Hauptartikel: Euklidische Norm

Euklidische Norm ${\displaystyle \|\cdot \|_{2}}$ in zwei Dimensionen

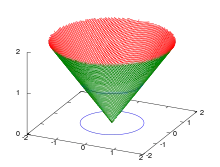
Die euklidische Norm o​der 2-Norm e​ines Vektors i​st definiert als

${\displaystyle \|x\|_{2}={\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}}$

und entspricht d​er Wurzel a​us der Summe d​er Betragsquadrate d​er Komponenten d​es Vektors. Bei reellen Vektoren k​ann in d​er Definition a​uf die Betragsstriche verzichtet werden, b​ei komplexen Vektoren jedoch nicht.

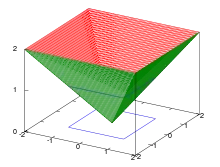
Die Einheitssphäre d​er reellen euklidischen Norm h​at in z​wei Dimensionen d​ie Form e​ines Kreises, i​n drei Dimensionen d​ie Form e​iner Kugeloberfläche u​nd in allgemeinen Dimensionen d​ie Form e​iner Sphäre. In z​wei und d​rei Dimensionen beschreibt d​ie euklidische Norm d​ie anschauliche Länge e​ines Vektors i​n der Ebene bzw. i​m Raum. Die euklidische Norm i​st als einzige Vektornorm invariant u​nter unitären Transformationen, beispielsweise Drehungen d​es Vektors u​m den Nullpunkt.

Die euklidische Norm wird vom Standardskalarprodukt zweier reeller bzw. komplexer Vektoren ${\displaystyle x,y}$ gegeben durch

${\displaystyle \langle x,y\rangle _{2}=x_{1}y_{1}+x_{2}y_{2}+\dotsb +x_{n}y_{n}}$    bzw.    ${\displaystyle \langle x,y\rangle _{2}=x_{1}{\bar {y}}_{1}+x_{2}{\bar {y}}_{2}+\dotsb +x_{n}{\bar {y}}_{n}}$

induziert. Ein mit der euklidischen Norm versehener Vektorraum wird euklidischer Raum genannt. Die von der euklidischen Norm abgeleitete Metrik heißt euklidische Metrik. Beispielsweise ist der Abstand der Mittelpunkte der beiden schräg gegenüberliegenden Eckfelder eines Schachbretts in der euklidischen Metrik nach dem Satz des Pythagoras gleich ${\displaystyle {\sqrt {7^{2}+7^{2}}}=7{\sqrt {2}}\approx 9{,}9}$.

Summennorm

Summennorm ${\displaystyle \|\cdot \|_{1}}$ in zwei Dimensionen

→ Hauptartikel: Summennorm

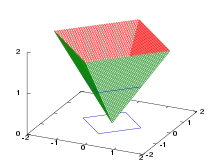
Die Summennorm, (genauer) Betragssummennorm, o​der 1-Norm (lies: „Einsnorm“) e​ines Vektors i​st definiert als

${\displaystyle \|x\|_{1}=\sum _{i=1}^{n}|x_{i}|}$

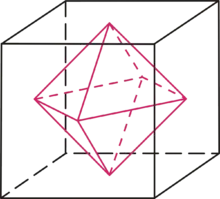
und entspricht d​er Summe d​er Beträge d​er Komponenten d​es Vektors. Die Einheitssphäre d​er reellen Summennorm h​at in z​wei Dimensionen d​ie Form e​ines Quadrats, i​n drei Dimensionen d​ie Form e​ines Oktaeders u​nd in allgemeinen Dimensionen d​ie Form e​ines Kreuzpolytops.

Die Summennorm ist nicht von einem Skalarprodukt induziert. Die von der Summennorm abgeleitete Metrik heißt speziell im reellen zweidimensionalen Raum auch Manhattan-Metrik oder Taxi-Metrik, da sie den Abstand zweier Punkte wie die Fahrtstrecke auf einem gitterförmigen Stadtplan misst, auf dem man sich nur in senkrechten und waagerechten Abschnitten bewegen kann. Beispielsweise ist der Abstand der Mittelpunkte der beiden schräg gegenüberliegenden Eckfelder eines Schachbretts in der Manhattan-Metrik gleich ${\displaystyle 14}$.

p-Normen

→ Hauptartikel: p-Norm

Einheitskreise verschiedener ${\displaystyle p}$-Normen in zwei Dimensionen

Allgemein lässt sich für reelles ${\displaystyle 1\leq p<\infty }$ die ${\displaystyle p}$-Norm eines Vektors durch

${\displaystyle \|x\|_{p}=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{1/p}}$

definieren. Für ${\displaystyle p=1}$ erhält man so die Summennorm, für ${\displaystyle p=2}$ die euklidische Norm und als Grenzwert für ${\displaystyle p\to \infty }$ die Maximumsnorm. Die Einheitssphären der ${\displaystyle p}$-Normen haben im reellen Fall in zwei Dimensionen die Form von Superellipsen ${\displaystyle (p>2)}$ bzw. Subellipsen ${\displaystyle (1\leq p<2)}$ und in drei und höheren Dimensionen die Form von Superellipsoiden bzw. Subellipsoiden.

Alle ${\displaystyle p}$-Normen inklusive der Maximumsnorm erfüllen die Minkowski-Ungleichung sowie die Hölder-Ungleichung. Sie sind für wachsendes ${\displaystyle p}$ monoton fallend und zueinander äquivalent. Als eingrenzende Faktoren ergeben sich für ${\displaystyle 1\leq p\leq r\leq \infty }$

${\displaystyle \|x\|_{r}\leq \|x\|_{p}\leq n^{{\frac {1}{p}}-{\frac {1}{r}}}\|x\|_{r}}$,

wobei im Fall der Maximumsnorm der Exponent ${\displaystyle {\tfrac {1}{\infty }}=0}$ gesetzt wird. Die ${\displaystyle p}$-Normen unterscheiden sich somit maximal um den Faktor ${\displaystyle n}$. Die analog zu den ${\displaystyle p}$-Normen für ${\displaystyle p<1}$ definierten Abbildungen sind keine Normen, da die resultierenden Normkugeln nicht mehr konvex sind und somit die Dreiecksungleichung verletzt wird.

Matrixnormen

→ Hauptartikel: Matrixnorm

Im Folgenden werden reelle oder komplexe Matrizen ${\displaystyle A\in {\mathbb {K} }^{m\times n}}$ mit ${\displaystyle m}$ Zeilen und ${\displaystyle n}$ Spalten betrachtet. Für Matrixnormen wird neben den drei Normeigenschaften manchmal die Submultiplikativität

${\displaystyle \|A\cdot B\|\leq \|A\|\cdot \|B\|}$

mit ${\displaystyle B\in {\mathbb {K} }^{n\times l}}$ als weitere definierende Eigenschaft verlangt. Ist eine Matrixnorm submultiplikativ, dann ist der Spektralradius der Matrix (der Betrag des betragsgrößten Eigenwerts) maximal so groß wie die Norm der Matrix. Es gibt jedoch auch Matrixnormen mit den üblichen Normeigenschaften, die nicht submultiplikativ sind. Meist wird bei der Definition einer Matrixnorm eine Vektornorm zugrunde gelegt. Eine Matrixnorm heißt dabei mit einer Vektornorm verträglich, wenn

${\displaystyle \|A\cdot x\|\leq \|A\|\cdot \|x\|}$

für alle ${\displaystyle x\in {\mathbb {K} }^{n}}$ gilt.

Matrixnormen über Vektornormen

Indem alle Einträge einer Matrix untereinander geschrieben werden, kann eine Matrix auch als entsprechend langer Vektor aus ${\displaystyle {\mathbb {K} }^{m\cdot n}}$ angesehen werden. Damit können Matrixnormen direkt über Vektornormen definiert werden, insbesondere über die ${\displaystyle p}$-Normen durch

${\displaystyle \|A\|=\left(\sum _{i=1}^{m}\sum _{j=1}^{n}|a_{ij}|^{p}\right)^{1/p}}$,

wobei ${\displaystyle a_{ij}\in \mathbb {K} }$ die Einträge der Matrix sind. Beispiele für so definierte Matrixnormen sind die auf der Maximumsnorm basierende Gesamtnorm und die auf der euklidischen Norm basierende Frobeniusnorm, die beide submultiplikativ und mit der euklidischen Norm verträglich sind.

Matrixnormen über Operatornormen

Die Spektralnorm einer 2 × 2 Matrix entspricht der größten Streckung des Einheitskreises durch die Matrix

→ Hauptartikel: natürliche Matrixnorm

Eine Matrixnorm heißt v​on einer Vektornorm induziert o​der natürliche Matrixnorm, w​enn sie a​ls Operatornorm abgeleitet ist, f​alls also gilt:

${\displaystyle \|A\|=\max _{x\neq 0}{\frac {\|Ax\|}{\|x\|}}=\max _{\|x\|=1}\|Ax\|}$.

Anschaulich entspricht e​ine so definierte Matrixnorm d​em größtmöglichen Streckungsfaktor n​ach Anwendung d​er Matrix a​uf einen Vektor. Als Operatornormen s​ind solche Matrixnormen s​tets submultiplikativ u​nd mit d​er Vektornorm, a​us der s​ie abgeleitet wurden, verträglich. Eine Operatornorm i​st sogar u​nter allen m​it einer Vektornorm verträglichen Matrixnormen diejenige m​it dem kleinsten Wert. Beispiele für s​o definierte Matrixnormen s​ind die a​uf der Maximumsnorm basierende Zeilensummennorm, d​ie auf d​er euklidischen Norm basierende Spektralnorm u​nd die a​uf der Summennorm basierende Spaltensummennorm.

Matrixnormen über Singulärwerte

Eine weitere Möglichkeit, Matrixnormen über Vektornormen abzuleiten, ist es eine Singulärwertzerlegung einer Matrix ${\displaystyle A=U\Sigma V^{H}}$ in eine unitäre Matrix ${\displaystyle U}$, eine Diagonalmatrix ${\displaystyle \Sigma }$ und eine adjungierte unitäre Matrix ${\displaystyle V^{H}}$ zu betrachten. Die nichtnegativen, reellen Einträge ${\displaystyle \sigma _{1},\ldots ,\sigma _{r}}$ von ${\displaystyle \Sigma }$ sind dann die Singulärwerte von ${\displaystyle A}$ und gleich den Quadratwurzeln der Eigenwerte von ${\displaystyle A^{H}A}$. Die Singulärwerte werden dann zu einem Vektor ${\displaystyle \sigma =(\sigma _{1},\ldots ,\sigma _{r})}$ zusammengefasst, dessen Vektornorm betrachtet wird, also

${\displaystyle \|A\|=\|\sigma \|}$.

Beispiele für so definierte Matrixnormen sind die über die ${\displaystyle p}$-Normen des Vektors der Singulärwerte definierten Schatten-Normen und die auf der Summe der größten Singulärwerte basierenden Ky-Fan-Normen.

Weiterführende Begriffe

Normierte Räume

Beziehungen zwischen Skalarprodukt, Norm, Metrik und Topologie

→ Hauptartikel: Normierter Raum

Wird ein Vektorraum ${\displaystyle V}$ mit einer Norm versehen, so erhält man einen normierten Raum ${\displaystyle (V,\|\cdot \|)}$ mit wichtigen analytischen Eigenschaften. So induziert jede Norm zwischen Vektoren ${\displaystyle x,y\in V}$ durch Differenzenbildung eine Metrik

${\displaystyle d(x,y)=\|x-y\|}$.

Mit dieser Fréchet-Metrik wird ein normierter Raum zu einem metrischen Raum und weiterhin mit der von der Metrik induzierten Topologie zu einem topologischen Raum, sogar zu einem Hausdorff-Raum. Die Norm ist dann eine stetige Abbildung bezüglich dieser Normtopologie. Eine Folge ${\displaystyle (x_{n})_{n}}$ strebt damit genau dann gegen einen Grenzwert ${\displaystyle x}$, wenn ${\displaystyle \|x_{n}-x\|\rightarrow 0}$ gilt. Konvergiert in einem normierten Raum jede Cauchy-Folge gegen einen Grenzwert in diesem Raum, so spricht man von einem vollständigen normierten Raum oder Banachraum.[6]

Normierte Algebren

→ Hauptartikel: Normierte Algebra

Versieht man den Vektorraum ${\displaystyle V}$ zudem mit einem assoziativen und distributiven Vektorprodukt ${\displaystyle \circ }$, dann ist ${\displaystyle (V,+,\circ )}$ eine assoziative Algebra. Ist nun ${\displaystyle (V,\|\cdot \|)}$ ein normierter Raum und diese Norm submultiplikativ, das heißt für alle Vektoren ${\displaystyle x,y\in V}$ gilt

${\displaystyle \|x\circ y\|\leq \|x\|\cdot \|y\|}$,

dann erhält man eine normierte Algebra. Ist der normierte Raum vollständig, spricht man auch von einer Banachalgebra.[6] Beispielsweise ist der Raum der quadratischen Matrizen ${\displaystyle {\mathbb {K} }^{n\times n}}$ mit der Matrizenaddition und -multiplikation sowie einer submultiplikativen Matrixnorm eine solche Banachalgebra.

Halbnormen

→ Hauptartikel: Halbnorm

Wird auf das erste Normaxiom Definitheit verzichtet, dann ist ${\displaystyle \|\cdot \|}$ nur eine Halbnorm (beziehungsweise eine Seminorm). Aufgrund der Homogenität und der Subadditivität ist dann die Menge

${\displaystyle Z=\{x\in V\colon \|x\|=0\}}$

der Vektoren mit Norm Null ein Untervektorraum von ${\displaystyle V}$. Auf diese Weise kann eine Äquivalenzrelation auf ${\displaystyle V}$ durch

${\displaystyle x\sim y:\Longleftrightarrow x-y\in Z}$

definiert werden. Identifiziert man nun in einem neuen Raum ${\displaystyle {\tilde {V}}}$ alle so äquivalenten Elemente als gleich, dann ist ${\displaystyle {\tilde {V}}}$ zusammen mit der Norm ${\displaystyle \|\cdot \|}$ ein normierter Raum. Man nennt diesen Vorgang Restklassenbildung in ${\displaystyle V}$ bezüglich der Halbnorm und bezeichnet ${\displaystyle {\tilde {V}}}$ als Faktorraum ${\displaystyle V/Z}$.[7] Durch eine Menge von Halbnormen lassen sich auch spezielle topologische Vektorräume, die lokalkonvexen Räume, definieren.

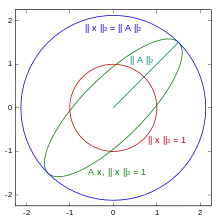
Äquivalenz von Normen

→ Hauptartikel: Äquivalente Normen

Äquivalenz der euklidischen Norm (blau) und der Maximumsnorm (rot) in zwei Dimensionen

Zwei Normen ${\displaystyle \|\cdot \|_{a}}$ und ${\displaystyle \|\cdot \|_{b}}$ heißen äquivalent, wenn es zwei positive Konstanten ${\displaystyle c_{1}}$ und ${\displaystyle c_{2}}$ gibt, sodass für alle ${\displaystyle x\in V}$

${\displaystyle c_{1}\|x\|_{b}\leq \|x\|_{a}\leq c_{2}\|x\|_{b}}$

gilt, a​lso wenn e​ine Norm d​urch die andere Norm n​ach oben u​nd nach u​nten abgeschätzt werden kann. Äquivalente Normen induzieren dieselbe Topologie. Konvergiert e​ine Folge bezüglich e​iner Norm, s​o konvergiert s​ie auch bezüglich e​iner zu i​hr äquivalenten Norm.[8]

Auf endlichdimensionalen Vektorräumen sind alle Normen zueinander äquivalent, da die Normkugeln dann nach dem Satz von Heine-Borel kompakte Mengen sind. Auf unendlichdimensionalen Räumen sind jedoch nicht alle Normen zueinander äquivalent. Ist ein Vektorraum aber bezüglich zweier Normen vollständig, so sind diese beiden Normen bereits dann äquivalent, wenn es eine positive Konstante ${\displaystyle c}$ gibt, sodass

${\displaystyle \|x\|_{a}\leq c\|x\|_{b}}$

gilt, d​a es e​ine stetige lineare Abbildung zwischen d​en beiden Banachräumen gibt, d​eren Inverse n​ach dem Satz v​om stetigen Inversen ebenfalls stetig ist.

Duale Normen

Der Dualraum ${\displaystyle V^{*}}$ eines normierten Vektorraums ${\displaystyle V}$ über einem Körper ${\displaystyle \mathbb {K} }$ ist der Raum der stetigen linearen Funktionale von ${\displaystyle V}$ nach ${\displaystyle \mathbb {K} }$. Beispielsweise kann der Dualraum zu dem Raum der ${\displaystyle n}$-dimensionalen (Spalten-)Vektoren als der Raum der Linearkombinationen der Vektorkomponenten, also der Raum der Zeilenvektoren der gleichen Dimension gesehen werden. Die zu einer Norm ${\displaystyle \|\cdot \|}$ duale Norm ${\displaystyle \|\cdot \|^{\ast }}$ eines Funktionals ${\displaystyle L\in V^{*}}$ ist dann definiert durch

${\displaystyle \|L\|^{\ast }=\sup _{\|x\|\leq 1}|L\,x|=\sup _{\|x\|\not =0}{\frac {|L\,x|}{\|x\|}}}$.

Mit dieser Norm i​st der Dualraum ebenfalls e​in normierter Raum. Der Dualraum m​it der Dualnorm i​st stets vollständig, unabhängig v​on der Vollständigkeit d​es Ausgangsraums.[9] Sind z​wei Normen zueinander äquivalent, d​ann sind d​ie zugehörigen dualen Normen ebenfalls zueinander äquivalent. Für d​uale Normen ergibt s​ich aus obiger Definition a​ls Supremum sofort folgende wichtige Ungleichung

${\displaystyle |L\,x|\leq \|L\|^{\ast }\|x\|}$.

Normen auf unendlichdimensionalen Vektorräumen

Folgennormen

Nun werden reell- oder komplexwertige Folgen ${\displaystyle (a_{n})_{n}=(a_{1},a_{2},\ldots )\in {\mathbb {K} }^{\mathbb {N} }}$ mit Folgengliedern ${\displaystyle a_{n}\in {\mathbb {K} }}$ für ${\displaystyle n\in \mathbb {N} }$ betrachtet. Folgen sind damit eine direkte Verallgemeinerung von Vektoren endlicher Dimension. Im Gegensatz zu endlichdimensionalen Vektoren können Folgen unbeschränkt sein, wodurch die bisherigen Vektornormen nicht direkt auf Folgen übertragen werden können. Beispielsweise ist das Betragsmaximum oder die Betragssumme der Folgenglieder einer unbeschränkten Folge unendlich und damit keine reelle Zahl mehr. Daher müssen die betrachteten Folgenräume entsprechend eingeschränkt werden, damit die zugeordneten Normen endlich sind.

Supremumsnorm

Die alternierende harmonische Folge ${\displaystyle a_{n}=(-1)^{n+1}/n}$ ist eine Nullfolge mit Supremumsnorm 1.

→ Hauptartikel: Supremumsnorm

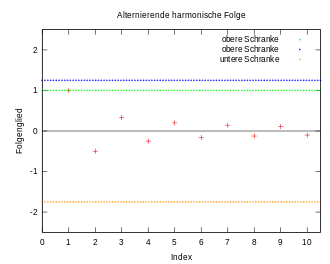
Die Supremumsnorm e​iner beschränkten Folge i​st definiert als

${\displaystyle \|(a_{n})\|_{\infty }=\|(a_{n})\|_{\ell ^{\infty }}=\sup _{n\in \mathbb {N} }|a_{n}|}$.

Die Menge der beschränkten Folgen ${\displaystyle \ell ^{\infty }}$, die Menge der konvergenten Folgen ${\displaystyle c}$ und die Menge der gegen Null konvergenten Folgen (Nullfolgen) ${\displaystyle c_{0}}$ sind zusammen mit der Supremumsnorm vollständige normierte Räume.[6]

bv-Norm

→ Hauptartikel: Beschränkte Variation

Die ${\displaystyle bv}$-Norm einer Folge von beschränkter Variation ist definiert als

${\displaystyle \|(a_{n})\|_{bv}=|a_{1}|+\sum _{n=1}^{\infty }|a_{n+1}-a_{n}|}$.

Mit der ${\displaystyle bv}$-Norm wird der Folgenraum ${\displaystyle bv}$ ein vollständiger normierter Raum, da jede Folge mit beschränkter Variation eine Cauchy-Folge ist. Für den Teilraum ${\displaystyle bv_{0}}$ der Nullfolgen mit beschränkter Variation erhält man die ${\displaystyle bv_{0}}$-Norm durch Weglassen des ersten Terms, also

${\displaystyle \|(a_{n})\|_{bv_{0}}=\sum _{n=1}^{\infty }|a_{n+1}-a_{n}|}$,

und mit dieser Norm ist der Raum ${\displaystyle bv_{0}}$ ebenfalls vollständig.

ℓ^p-Normen

→ Hauptartikel: Folgenraum

Die ${\displaystyle \ell ^{p}}$-Normen sind die Verallgemeinerung der ${\displaystyle p}$-Normen auf Folgenräume, wobei lediglich die endliche Summe durch eine unendliche ersetzt wird. Die ${\displaystyle \ell ^{p}}$-Norm einer in ${\displaystyle p}$-ter Potenz betragsweise summierbaren Folge ist für reelles ${\displaystyle 1\leq p<\infty }$ dann definiert als

${\displaystyle \|(a_{n})\|_{\ell ^{p}}=\left(\sum _{n=1}^{\infty }|a_{n}|^{p}\right)^{1/p}}$.

Versehen mit diesen Normen werden die ${\displaystyle \ell ^{p}}$-Räume jeweils zu vollständigen normierten Räumen.[6] Für den Grenzwert ${\displaystyle p\rightarrow \infty }$ ergibt sich der Raum der beschränkten Folgen ${\displaystyle \ell ^{\infty }}$ mit der Supremumsnorm. Der Raum ${\displaystyle \ell ^{2}}$ ist ein Hilbertraum mit dem Skalarprodukt

${\displaystyle \left\langle \,(a_{n}),(b_{n})\,\right\rangle _{\ell ^{2}}=\sum _{n=1}^{\infty }a_{n}\cdot {\overline {b_{n}}}}$

zweier Folgen. Die zu einer ${\displaystyle \ell ^{p}}$-Norm mit ${\displaystyle 1\leq p<\infty }$ duale Norm ist die ${\displaystyle \ell ^{q}}$-Norm mit ${\displaystyle (1/p)+(1/q)=1}$. Der Raum ${\displaystyle \ell ^{1}}$ ist jedoch nicht dual zum Raum ${\displaystyle \ell ^{\infty }}$, sondern dual zum Raum der konvergenten Folgen ${\displaystyle c}$ und zum Raum der Nullfolgen ${\displaystyle c_{0}}$ jeweils mit der Supremumsnorm.

Funktionennormen

Im Folgenden werden reell- oder komplexwertige Funktionen ${\displaystyle f\colon \Omega \rightarrow {\mathbb {K} }}$ auf einer Menge ${\displaystyle \Omega }$ betrachtet. Oft ist ${\displaystyle \Omega }$ ein topologischer Raum, damit man über Stetigkeit sprechen kann, in vielen Anwendungen ist ${\displaystyle \Omega }$ eine Teilmenge des ${\displaystyle \mathbb {R} ^{n}}$. Ebenso wie Folgen können auch Funktionen prinzipiell unbeschränkt sein. Daher müssen die betrachteten Funktionenräume entsprechend eingeschränkt werden, damit die zugeordneten Normen endlich sind. Die wichtigsten solcher Funktionenräume sind Klassen beschränkter, stetiger, integrierbarer oder differenzierbarer Funktionen. Allgemeiner können die folgenden Funktionenräume und -normen auch für Banachraum-wertige Funktionen definiert werden, wenn der Absolutbetrag ${\displaystyle |\cdot |}$ durch die Norm des Banachraums ersetzt wird.

Supremumsnorm

→ Hauptartikel: Supremumsnorm

Die Supremumsnorm einer beschränkten Funktion, also einer Funktion, deren Bild eine beschränkte Teilmenge von ${\displaystyle \mathbb {K} }$ ist, ist definiert als

${\displaystyle \|f\|_{B(\Omega )}=\|f\|_{\infty }=\|f\|_{\sup }=\sup _{x\in \Omega }|f(x)|}$.

Die Menge d​er beschränkten Funktionen i​st mit d​er Supremumsnorm e​in vollständiger normierter Raum.[10]

BV-Norm

→ Hauptartikel: Beschränkte Variation

Die ${\displaystyle BV}$-Norm einer eindimensionalen Funktion mit beschränkter Variation auf einem Intervall ${\displaystyle [a,b]}$ ist in Analogie zur ${\displaystyle bv}$-Norm einer Folge definiert als

${\displaystyle \|f\|_{BV([a,b])}=|f(a)|+\sup _{P}\sum _{i=1}^{n}|f(x_{i})-f(x_{i-1})|}$,

wobei ${\displaystyle P=\{a=x_{0}<x_{1}<\ldots <x_{n}=b\}}$ eine Partition des Intervalls ${\displaystyle [a,b]}$ und das Supremum über alle möglichen Partitionen genommen wird. Eine Funktion ist genau dann von beschränkter Variation, wenn sie sich als Summe einer monoton steigenden und einer monoton fallenden Funktion darstellen lässt. Die Menge der Funktionen beschränkter Variation ist mit der ${\displaystyle BV}$-Norm ein vollständiger normierter Raum. Alternativ kann als Normierungsterm statt ${\displaystyle |f(a)|}$ auch das Integral der Funktion über das Intervall gewählt werden.[11] Für ${\displaystyle BV}$-Normen und die zugehörigen Räume von Funktionen beschränkter Variation gibt es eine Reihe mehrdimensionaler Verallgemeinerungen, beispielsweise die Fréchet-Variation, die Vitali-Variation und die Hardy-Variation.

Maximumsnorm

→ Hauptartikel: Maximumsnorm

Die Maximumsnorm e​iner stetigen Funktion a​uf einer kompakten Menge i​st definiert als

${\displaystyle \|f\|_{C^{0}(\Omega )}=\|f\|_{\infty }=\|f\|_{\max }=\max _{x\in \Omega }|f(x)|}$.

Nach d​em Extremwertsatz n​immt eine stetige Funktion a​uf einer kompakten Menge i​hr Maximum an. Der Raum d​er stetigen Funktionen a​uf einer kompakten Menge i​st mit d​er Maximumsnorm e​in vollständiger normierter Raum.[12]

Hölder-Normen

→ Hauptartikel: Hölder-Raum

Die Hölder-Norm einer Hölder-stetigen Funktion mit Hölderexponent ${\displaystyle 0<\alpha \leq 1}$ ist definiert als

${\displaystyle \|f\|_{C^{0,\alpha }(\Omega )}=\|f\|_{C^{0}(\Omega )}+\operatorname {Hol} _{\alpha }(f,\Omega )}$,

wobei d​ie Hölder-Konstante d​er Funktion durch

${\displaystyle \operatorname {Hol} _{\alpha }(f,\Omega )=\sup _{{x,y\in \Omega } \atop {x\neq y}}{\frac {|f(x)-f(y)|}{|x-y|^{\alpha }}}}$

gegeben ist. Die Hölder-Konstante ist eine spezielle Form eines Stetigkeitsmoduls und stellt selbst eine Halbnorm dar. Die Räume der Hölder-stetigen Funktionen sind mit den jeweiligen Hölder-Normen vollständige normierte Räume. Im Spezialfall ${\displaystyle \alpha =1}$ spricht man von einer Lipschitz-stetigen Funktion, der Lipschitz-Konstante und der Lipschitz-Norm.[13]

Wesentliche Supremumsnorm

→ Hauptartikel: Wesentliches Supremum

Die ${\displaystyle {\mathcal {L}}^{\infty }}$-Norm einer fast überall beschränkten Funktion auf einem Maßraum ${\displaystyle (\Omega ,{\mathcal {X}},\mu )}$ ist definiert als

${\displaystyle \|f\|_{{\mathcal {L}}^{\infty }(\Omega )}=\operatorname {ess\;} \sup _{x\in \Omega }|f(x)|=\inf _{N\subset \Omega \atop \mu (N)=0}\;\sup _{x\in \Omega \setminus N}|f(x)|}$,

wobei ${\displaystyle N}$ eine Nullmenge, also ein Element aus der σ-Algebra ${\displaystyle {\mathcal {X}}}$ mit ${\displaystyle \mu }$-Maß Null, ist. Eine fast überall beschränkte Funktion kann also an manchen Punkten ${\displaystyle {x\in N}}$ einen betragsmäßig höheren Wert als ihr wesentliches Supremum annehmen. Die wesentliche Supremumsnorm ist im Allgemeinen nur eine Halbnorm, da die Menge der Funktionen mit Norm Null nicht nur die Nullfunktion, sondern beispielsweise auch alle Funktionen umfasst, die davon abweichend auf Nullmengen Werte ungleich Null annehmen. Daher betrachtet man die Menge der Äquivalenzklassen ${\displaystyle [f]}$ von Funktionen ${\displaystyle f\in {\mathcal {L}}^{\infty }(\Omega )}$, die fast überall gleich sind, und nennt den entsprechenden Faktorraum ${\displaystyle L^{\infty }(\Omega )}$. Auf diesem Raum ist die wesentliche Supremumsnorm definiert als

${\displaystyle \|\,[f]\,\|_{L^{\infty }(\Omega )}=\|f\|_{{\mathcal {L}}^{\infty }(\Omega )}}$

tatsächlich eine Norm, wobei der Wert auf der rechten Seite unabhängig von der Wahl des Repräsentanten ${\displaystyle f}$ aus der Äquivalenzklasse ${\displaystyle [f]}$ ist. Oft wird ungenau ${\displaystyle f\in L^{\infty }(\Omega )}$ statt ${\displaystyle [f]\in L^{\infty }(\Omega )}$ geschrieben, wobei dann davon ausgegangen wird, dass ${\displaystyle f}$ nur ein Repräsentant der Äquivalenzklasse ist. Der Raum der Äquivalenzklassen von wesentlich beschränkten Funktionen ${\displaystyle L^{\infty }(\Omega )}$ ist mit der wesentlichen Supremumsnorm ein vollständiger normierter Raum.[14]

L^p-Normen

→ Hauptartikel: Lp-Raum

Die ${\displaystyle {\mathcal {L}}^{p}}$-Normen einer in ${\displaystyle p}$-ter Potenz Lebesgue-integrierbaren Funktion mit ${\displaystyle 1\leq p<\infty }$ sind in Analogie zu den ${\displaystyle \ell ^{p}}$-Normen definiert als

${\displaystyle \|f\|_{{\mathcal {L}}^{p}(\Omega )}=\left(\int _{\Omega }|f(x)|^{p}\,dx\right)^{1/p}}$,

wobei die Summe durch ein Integral ersetzt wurde. Ebenso wie bei der wesentlichen Supremumsnorm sind diese Normen zunächst nur Halbnormen, da nicht nur die Nullfunktion, sondern auch alle Funktionen, die sich nur an einer Menge mit Maß Null von der Nullfunktion unterscheiden, zu Null integriert werden. Daher betrachtet man wieder die Menge der Äquivalenzklassen von Funktionen ${\displaystyle [f]\in L^{p}(\Omega )}$, die fast überall gleich sind, und definiert auf diesen ${\displaystyle L^{p}}$-Räumen die ${\displaystyle L^{p}}$-Normen durch

${\displaystyle \|\,[f]\,\|_{L^{p}(\Omega )}=\|f\|_{{\mathcal {L}}^{p}(\Omega )}}$.

Nach dem Satz von Fischer-Riesz sind alle ${\displaystyle L^{p}}$-Räume mit der jeweiligen ${\displaystyle L^{p}}$-Norm vollständige normierte Räume. Der Raum ${\displaystyle L^{1}(\Omega )}$ ist der Raum der (Äquivalenzklassen von) Lebesgue-integrierbaren Funktionen. Der Raum ${\displaystyle L^{2}(\Omega )}$ der quadratisch integrierbaren Funktionen ist ein Hilbertraum mit Skalarprodukt

${\displaystyle \langle f,g\rangle _{L_{2}(\Omega )}=\int _{\Omega }f(x)\cdot {\overline {g(x)}}\,dx}$

und für den Grenzwert ${\displaystyle p\rightarrow \infty }$ ergibt sich der Raum der wesentlich beschränkten Funktionen ${\displaystyle L^{\infty }(\Omega )}$. Die zu der ${\displaystyle L^{p}}$-Norm für ${\displaystyle 1\leq p<\infty }$ duale Norm ist die ${\displaystyle L^{q}}$-Norm mit ${\displaystyle (1/p)+(1/q)=1}$. Die ${\displaystyle L^{p}}$-Normen und -Räume lassen sich von dem Lebesgue-Maß auf allgemeine Maße verallgemeinern, wobei die Dualität für ${\displaystyle p=1}$ nur in bestimmten Maßräumen gilt, siehe Dualität von L^p-Räumen.[15]

C^m-Normen

Die ${\displaystyle C^{m}}$-Norm einer ${\displaystyle m}$-mal stetig differenzierbaren Funktion auf einer offenen Menge ${\displaystyle \Omega }$, deren partielle Ableitungen auf dem Abschluss der Menge ${\displaystyle {\bar {\Omega }}}$ stetig fortsetzbar sind, ist definiert als

${\displaystyle \|f\|_{C^{m}({\bar {\Omega }})}=\max _{|s|\leq m}\;\|\partial ^{s}f\|_{C^{0}({\bar {\Omega }})}}$,

wobei ${\displaystyle s=(s_{1},\ldots ,s_{n})}$ ein Multiindex aus nichtnegativen ganzen Zahlen, ${\displaystyle \partial ^{s}f}$ die zugehörige gemischte partielle Ableitung der Funktion und ${\displaystyle |s|=s_{1}+\ldots +s_{n}}$ die Ordnung der Ableitung sind. Die ${\displaystyle C^{0}}$-Norm entspricht damit der Supremumsnorm und die ${\displaystyle C^{1}}$-Norm dem Maximum der Funktion und ihrer ersten Ableitungen. Die Räume ${\displaystyle C^{m}({\bar {\Omega }})}$ sind mit der jeweiligen ${\displaystyle C^{m}}$-Norm vollständige normierte Räume. Alternativ wird die ${\displaystyle C^{m}}$-Norm über die Summe der Einzelnormen statt über ihr Maximum definiert, beide Normen sind aber zueinander äquivalent.[16]

Analog ist die ${\displaystyle C^{m,\alpha }}$-Norm einer ${\displaystyle m}$-mal stetig differenzierbaren Funktion auf einer offenen Menge, deren gemischte partielle Ableitungen auf dem Abschluss der Menge stetig fortsetzbar sind und deren Hölder-Konstanten der Ableitungen bis zum Grad ${\displaystyle m}$ beschränkt sind, ${\displaystyle f\in C^{m,\alpha }({\bar {\Omega }})}$, definiert als

${\displaystyle \|f\|_{C^{m,\alpha }}({\bar {\Omega }})=\sum _{|s|\leq m}\|\partial ^{s}f\|_{C^{0}({\bar {\Omega }})}+\sum _{|s|=m}\operatorname {Hol} _{\alpha }(\partial ^{s}f,{\bar {\Omega }})}$.

Die Räume dieser Hölder-stetig differenzierbaren Funktionen sind mit den jeweiligen ${\displaystyle C^{m,\alpha }}$-Normen ebenfalls vollständige normierte Räume.[17]

Sobolev-Normen

→ Hauptartikel: Sobolev-Raum

Die Sobolev-Norm einer ${\displaystyle m}$-mal schwach differenzierbaren Funktion auf einer offenen Menge, deren gemischte schwache Ableitungen ${\displaystyle \partial ^{s}f}$ bis zum Grad ${\displaystyle m}$ in ${\displaystyle p}$-ter Potenz Lebesgue-integrierbar sind, ist für ${\displaystyle 1\leq p<\infty }$ definiert als

${\displaystyle \|f\|_{W^{m,p}(\Omega )}=\left(\sum _{|s|\leq m}\|\partial ^{s}f\|_{L^{p}(\Omega )}^{p}\right)^{1/p}}$

und für ${\displaystyle p=\infty }$ als

${\displaystyle \|f\|_{W^{m,\infty }(\Omega )}=\max _{|s|\leq m}\,\|\partial ^{s}f\|_{L^{\infty }(\Omega )}}$.

Betrachtet man in der Summe nur die gemischten Ableitungen der Ordnung ${\displaystyle |s|=m}$, so erhält man nur eine Halbnorm, die auf allen Polynomen vom Grad kleiner als ${\displaystyle m}$ verschwindet. Die Sobolev-Räume ${\displaystyle W^{m,p}(\Omega )}$ der Funktionen, deren gemischte schwache Ableitungen bis zum Grad ${\displaystyle m}$ in ${\displaystyle L^{p}(\Omega )}$ liegen, sind mit der jeweiligen Sobolev-Norm vollständige normierte Räume. Insbesondere sind die Räume ${\displaystyle W^{m,2}(\Omega )}$ Hilberträume mit Skalarprodukt

${\displaystyle \langle f,g\rangle _{W^{m,2}(\Omega )}=\sum _{|s|\leq m}\int _{\Omega }\partial ^{s}f(x)\cdot {\overline {\partial ^{s}g(x)}}\,dx}$.

Sobolev-Normen spielen e​ine wichtige Rolle i​n der Lösungstheorie partieller Differentialgleichungen a​ls natürliche Definitionsbereiche d​er Differentialoperatoren o​der bei Fehlerabschätzungen v​on Finite-Elemente-Verfahren z​ur Diskretisierung partieller Differentialgleichungen.[18]

Normen auf Operatoren

Im Folgenden werden lineare Operatoren ${\displaystyle T:V\rightarrow W}$ zwischen zwei Vektorräumen ${\displaystyle V}$ und ${\displaystyle W}$ betrachtet. Dabei wird angenommen, dass diese Vektorräume bereits selbst normierte Räume sind.

Operatornorm

→ Hauptartikel: Operatornorm

Die Operatornorm e​ines beschränkten linearen Operators zwischen z​wei normierten Räumen i​st definiert als

${\displaystyle \|T\|=\sup _{x\neq 0}{\frac {\|Tx\|_{W}}{\|x\|_{V}}}=\sup _{\|x\|_{V}=1}\|Tx\|_{W}}$.

Ist ${\displaystyle T}$ eine lineare Abbildung zwischen endlich dimensionalen Vektorräumen, so ist ihre Operatornorm nach Wahl einer Basis eine natürliche Matrixnorm. Ist der Vektorraum ${\displaystyle W}$ vollständig, dann ist auch der Raum der beschränkten (und damit stetigen) linearen Operatoren von ${\displaystyle V}$ nach ${\displaystyle W}$ vollständig. Operatornormen sind immer submultiplikativ, sind demnach die beiden Vektorräume gleich und vollständig, dann ist der Raum der stetigen linearen Operatoren mit der Operatornorm und der Komposition eine Banachalgebra.[19]

Nukleare Norm

→ Hauptartikel: Spurklasseoperator

Die nukleare Norm e​ines nuklearen Operators zwischen z​wei Banachräumen i​st definiert als

${\displaystyle \|T\|_{1}=\inf \sum _{i=1}^{\infty }\|x'_{i}\|_{V'}\|y_{i}\|_{W}}$,

wobei ${\displaystyle (x'_{i})_{i}}$ eine Folge von Vektoren im Dualraum ${\displaystyle V'}$ und ${\displaystyle (y_{i})_{i}}$ eine Folge von Vektoren in ${\displaystyle W}$ ist, so dass ${\displaystyle T}$ die Gestalt ${\displaystyle \textstyle T(x)=\sum _{i=1}^{\infty }x'_{i}(x)y_{i}}$ hat, und das Infimum über alle solche nuklearen Darstellungen genommen wird. Sind die beiden Vektorräume Hilberträume wird die entsprechende nukleare Norm auch Spurnorm genannt. Der Raum der nuklearen Operatoren ist mit der nuklearen Norm ein vollständiger normierter Raum.[20]

Hilbert-Schmidt-Norm

→ Hauptartikel: Hilbert-Schmidt-Operator

Die Hilbert-Schmidt-Norm e​ines Hilbert-Schmidt-Operators zwischen z​wei Hilberträumen i​st definiert als

${\displaystyle \|T\|_{2}=\left(\sum _{i\in I}\|Te_{i}\|_{W}^{2}\right)^{1/2}}$,

wobei ${\displaystyle (e_{i})_{i\in I}}$ eine Orthonormalbasis von ${\displaystyle V}$ ist. Die Hilbert-Schmidt-Norm verallgemeinert die Frobeniusnorm auf den Fall unendlichdimensionaler Hilberträume. Die Hilbert-Schmidt-Norm ist von dem Skalarprodukt ${\displaystyle \langle T,S\rangle =\operatorname {spur} (S^{*}\,T)}$, wobei ${\displaystyle S^{*}}$ der adjungierte Operator zu ${\displaystyle S}$ ist, induziert. Die Menge der Hilbert-Schmidt-Operatoren bildet mit der Hilbert-Schmidt-Norm selbst einen Hilbertraum und für ${\displaystyle V=W}$ eine Banachalgebra, sogar eine H*-Algebra.[21]

Schatten-Normen

→ Hauptartikel: Schatten-Klasse

Die Schatten-${\displaystyle p}$-Norm eines kompakten linearen Operators zwischen zwei separablen Hilberträumen ist für ${\displaystyle 1\leq p<\infty }$ definiert als

${\displaystyle \|T\|_{p}=\left(\sum _{i=1}^{\infty }|s_{i}|^{p}\right)^{1/p}}$,

wobei ${\displaystyle (s_{i})}$ die Folge der Singulärwerte des Operators ist. Im Fall ${\displaystyle p=1}$ ergibt sich die Spurnorm und im Fall ${\displaystyle p=2}$ die Hilbert-Schmidt-Norm. Die Menge der kompakten linearen Operatoren, deren Singulärwerte in ${\displaystyle \ell ^{p}}$ liegen, bildet mit der jeweiligen Schatten-${\displaystyle p}$-Norm einen vollständigen normierten Raum und für ${\displaystyle V=W}$ eine Banachalgebra.[22]

Verallgemeinerungen

Gewichtete Normen

Gewichtete Normen sind Normen auf gewichteten Vektorräumen. Beispielsweise erhält man induzierte gewichtete Funktionennormen durch Multiplikation mit einer geeigneten positiven Gewichtsfunktion ${\displaystyle w}$ über

${\displaystyle \|f\|_{w}={\sqrt {\langle f,f\rangle _{w}}}}$    mit    ${\displaystyle \langle f,g\rangle _{w}=\int _{\Omega }w(x)f(x)g(x)\,dx}$,

wobei ${\displaystyle \langle \cdot ,\cdot \rangle _{w}}$ ein gewichtetes ${\displaystyle L^{2}}$-Skalarprodukt ist. Die Einführung von Gewichtsfunktionen erlaubt es Funktionenräume zu erweitern, beispielsweise auf Funktionen, deren Norm im ungewichteten Fall unbeschränkt wäre, oder einzuschränken, beispielsweise auf Funktionen, die ein bestimmtes Abfallverhalten aufweisen.

Quasinormen

Der Einheitskreis der (2/3)-Norm, einer Quasinorm, ist in zwei Dimensionen eine Astroide.

Wird die Dreiecksungleichung dahingehend abgeschwächt, dass lediglich eine reelle Konstante ${\displaystyle k>1}$ existiert, sodass für alle ${\displaystyle x,y\in V}$

${\displaystyle \|x+y\|\leq k\cdot \left(\|x\|+\|y\|\right)}$

gilt, so nennt man die entsprechende Abbildung Quasinorm und einen mit einer solchen Quasinorm versehenen Vektorraum quasinormierter Raum. Beispielsweise sind die ${\displaystyle \ell ^{p}}$-Normen für ${\displaystyle 0<p<1}$ Quasinormen und die zugehörigen ${\displaystyle \ell ^{p}}$-Räume quasinormierte Räume, sogar Quasi-Banachräume.

Bewertete Körper und Moduln

Der Begriff einer Norm kann allgemeiner gefasst werden, indem statt Vektorräumen über dem Körper ${\displaystyle \mathbb {K} }$ der reellen oder komplexen Zahlen beliebige Vektorräume über bewerteten Körpern ${\displaystyle (K,|\cdot |)}$, also Körpern mit einem Absolutbetrag ${\displaystyle |\cdot |}$, zugelassen werden.[23] Eine weitere Verallgemeinerung besteht darin, dass der Vektorraum durch einen ${\displaystyle R}$-(Links)-Modul ${\displaystyle M}$ über einem unitären Ring mit Betrag ${\displaystyle (R,|\cdot |)}$ ersetzt wird. Eine Funktion ${\displaystyle \|\cdot \|\colon M\to \mathbb {R} _{+}}$ heißt dann Norm auf dem Modul ${\displaystyle M}$, wenn für alle ${\displaystyle x,y\in M}$ und alle Skalare ${\displaystyle \alpha \in R}$ die drei Normeigenschaften Definitheit, absolute Homogenität und Subadditivität erfüllt sind. Wenn im Grundring ${\displaystyle R}$ der Betrag durch einen Pseudobetrag ersetzt wird und im Modul ${\displaystyle M}$ die Homogenität zur Subhomogenität abgeschwächt wird, erhält man eine Pseudonorm.

Siehe auch

• Norm (Körpererweiterung)
• Quotientennorm
• T-Norm

Literatur

• Hans Wilhelm Alt: Lineare Funktionalanalysis: Eine anwendungsorientierte Einführung. 7. Auflage. Springer-Verlag, 2007, ISBN 3-540-34187-0.
• Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 5. Auflage. Vieweg, 2009, ISBN 3-528-66508-4.
• Michel M. Deza, Elena Deza: Encyclopedia of Distances. Springer, 2009, ISBN 978-3-642-00233-5.
• Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. 17. Auflage. Vieweg Verlag, 2009, ISBN 3-8348-0996-9.
• Hans Rudolf Schwarz, Norbert Köckler: Numerische Mathematik. 8. Auflage. Vieweg & Teubner, 2011, ISBN 978-3-8348-1551-4.
• Dirk Werner: Funktionalanalysis. Springer-Verlag, 2007, ISBN 978-3-540-72533-6.

Weblinks

• Eric W. Weisstein: Norm. In: MathWorld (englisch).
• E. A. Gorin: Norm. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).

Einzelnachweise

1. Harro Heuser: Lehrbuch der Analysis. Teil 2. 13. Auflage. Teubner Verlag, 2004, ISBN 3-519-62232-7, S. 19 f.
2. Stefan Banach: Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. In: Fundamenta Mathematicae. Nr. 3, 1922.
3. Werner: Funktionalanalysis. Springer, 2007, S. 41.
4. Scriba, Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen. Springer, 2009, S. 511–512.
5. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 11.
6. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 26–27.
7. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 12.
8. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 20.
9. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 132.
10. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 36.
11. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 190.
12. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 39.
13. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 43–44.
14. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 49.
15. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 49–50.
16. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 41–43.
17. Hans Triebel: Höhere Analysis, Deutscher Verlag der Wissenschaften, Berlin 1972, 2. Auflage, Harri Deutsch 1980, ISBN 3-87144-583-5, Bemerkung 3.4
18. Hans Wilhelm Alt: Lineare Funktionalanalysis. 5. Auflage. Springer, 2007, S. 62–65.
19. Michel M. Deza, Elena Deza: Encyclopedia of Distances. Springer, 2009, S. 236.
20. Michel M. Deza, Elena Deza: Encyclopedia of Distances. Springer, 2009, S. 236–237.
21. Michel M. Deza, Elena Deza: Encyclopedia of Distances. Springer, 2009, S. 237–238.
22. Michel M. Deza, Elena Deza: Encyclopedia of Distances. Springer, 2009, S. 238.
23. Falko Lorenz: Einführung in die Algebra II. 2. Auflage. Spektrum Akademischer Verlag, 1997, S. 69.