Euklidischer Abstand
Der euklidische Abstand ist der Abstandsbegriff der euklidischen Geometrie. Der euklidische Abstand zweier Punkte in der Ebene oder im Raum ist die zum Beispiel mit einem Lineal gemessene Länge einer Strecke, die diese zwei Punkte verbindet. Dieser Abstand ist invariant unter Bewegungen (Kongruenzabbildungen).

In kartesischen Koordinaten kann der euklidische Abstand mit Hilfe des Satzes von Pythagoras berechnet werden. Mit Hilfe der so gewonnenen Formel kann der Begriff des euklidischen Abstands auf -dimensionale euklidische und unitäre Vektorräume, euklidische Punkträume und Koordinatenräume verallgemeinert werden.
„Euklidisch“ heißt dieser Abstand in Abgrenzung zu allgemeineren Abstandsbegriffen, wie zum Beispiel:
- dem der hyperbolischen Geometrie,
- dem der riemannschen Geometrie,
- Abständen in normierten Vektorräumen,
- Abständen in beliebigen metrischen Räumen.
Euklidischer Raum

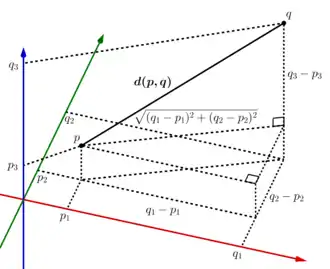
In der zweidimensionalen euklidischen Ebene oder im dreidimensionalen euklidischen Raum stimmt der euklidische Abstand mit dem anschaulichen Abstand überein. Im allgemeineren Fall des -dimensionalen euklidischen Raumes ist er für zwei Punkte oder Vektoren durch die euklidische Norm des Differenzvektors zwischen den beiden Punkten definiert. Sind die Punkte und durch die Koordinaten und gegeben, so gilt:
Ein bekannter Spezialfall der Berechnung eines euklidischen Abstandes für ist der Satz des Pythagoras.
Der euklidische Abstand ist eine Metrik und erfüllt insbesondere die Dreiecksungleichung. Neben dem euklidischen Abstand gibt es eine Reihe weiterer Abstandsmaße. Da der euklidische Abstand von einer Norm herrührt, nämlich der euklidischen Norm, ist er translationsinvariant.
In der Statistik ist der euklidische Abstand ein Spezialfall des gewichteten euklidischen Abstands und sein Quadrat ein Spezialfall des Mahalanobis-Abstands.
Beispiel
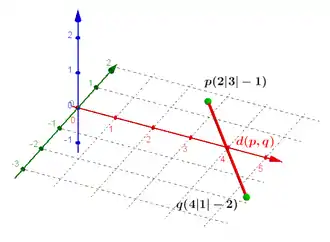
Der euklidische Abstand der beiden Punkte und ist
- .
Literatur
- Hermann Schichl, Roland Steinbauer: Einführung in das mathematische Arbeiten. 2. überarbeitete Auflage. Springer, 2012, ISBN 978-3-642-28646-9, S. 382 ff.
- Winfried Schröter: Neuere statistische Verfahren und Modellbildung in der Geoökologie. Springer, 2013, ISBN 978-3-322-83735-6, S. 120 ff.
- Elena Deza, Michel Marie Deza: Encyclopedia of Distances. Springer, 2009, ISBN 978-3-642-00233-5, S. 94
Weblinks
- Eric W. Weisstein: Distance. In: MathWorld (englisch).
- Eric W. Weisstein: Euclidean Metric. In: MathWorld (englisch).