Null

Null
	0
Darstellung
Dual	0
Oktal	0
Duodezimal	0
Hexadezimal	0
Morsecode	– – – – –
Arabisch	٠
Chinesisch	零, 〇
Indisch	०
Mathematische Eigenschaften
Vorzeichen	ohne
Parität	gerade
Faktorisierung	keine
Teiler	jede ganze Zahl

Die Zahl Null ist die Anzahl der Elemente in einer leeren Ansammlung von Objekten, mathematisch gesprochen die Kardinalität der leeren Menge. Null bezeichnet in der Mathematik je nach Kontext verschiedenartig definierte Objekte, die jedoch oft miteinander identifiziert werden können, d. h. als dasselbe Objekt angesehen, das verschiedene miteinander kompatible Eigenschaften vereint. Da Kardinalzahlen (Anzahl der Elemente einer Menge) mit speziellen Ordinalzahlen identifiziert werden, und die Null gerade die kleinste Kardinalzahl ist, wird die Null – im Gegensatz zum gängigen Sprachgebrauch – auch als erste Ordinalzahl gewählt. Als endliche Kardinal- und Ordinalzahl wird sie je nach Definition auch zu den natürlichen Zahlen gezählt. Die Null ist das neutrale Element bezüglich der Addition (anschaulich gesprochen die Differenz zweier gleicher Zahlen) in vielen Körpern, wie etwa den rationalen Zahlen, reellen Zahlen und komplexen Zahlen, und eine gängige Bezeichnung für ein neutrales Element in vielen algebraischen Strukturen, selbst wenn andere Elemente nicht mit gängigen Zahlen identifiziert werden. Als ganze Zahl ist die Null Nachfolgerin der Minus-Eins und Vorgängerin der Eins. Auf einer Zahlengeraden trennt der Nullpunkt die positiven von den negativen Zahlen. Die Null ist die einzige reelle Zahl, die weder positiv noch negativ ist. Die Zahl Null ist gerade.

0-km-Stein, Budapest

Dargestellt wird die Null durch die Ziffer „0“, deren Einführung Stellenwertsysteme wie die Dezimalzahlen erst möglich machte.[1][2][3]

Die Geschichte der Null

Erst die Erfindung eines Stellenwertsystems mit dem Lückenzeichen „0“ und die Betrachtung von „0“ als eigenständige Ziffer, die etwas darstellt, mit dem man wie mit anderen Zahlen rechnen konnte, führte zur Vorstellung, dass die Null „0“ eine Zahl sei. Damit war eine Grundlage für die weitere Entwicklung der Mathematik gelegt.

Babylonien

In der Perser- (539–331 v. Chr.) und hauptsächlich der Seleukidenzeit (305–63 v. Chr.) gab es als Vorstufe der Zahl Null ein Fehlzeichen im Sexagesimalsystem der Babylonier,[4] nämlich in sexagesimalen Zahlen an Stellen ohne Wert. Davor wurde es nur in altbabylonischer Zeit (um 1800–um 1500 v. Chr.) in manchen Texten verwendet, um Doppeldeutigkeiten wie sexagesimal 30,16 (= 30×60 + 16 = 1816) und 20,26 (= 20×60 + 26 = 1226) oder 10,36 (= 10×60 + 36 = 636) zu verhindern,[5] eine Stelle ohne Wert wurde dann durch eine Lücke dargestellt.[6] Meistens musste man aber aus dem Zusammenhang heraus auf das Fehlen von Stellen schließen, was jedoch nur sehr selten nötig war, denn in den erhaltenen Texten findet sich unter Tausenden von Zahlenangaben nur etwa ein Dutzend solcher Fälle.[7] Die sexagesimalen Zahlen der Babylonier hatten keine feste Größenordnung, so wurde z. B. dezimal 123 (= 2×60 + 3) genau so geschrieben wie 7380 (= 2×60² + 3×60) oder 2,05 (= 2 + 3/60). Nur in astronomischen Texten änderte sich dies ab 200 v. Chr. und das Fehlzeichen wurde dort auch am Ende von Zahlen verwendet.[8]

Bereits in altbabylonischer Zeit[9] traten außerdem in algebraischen Texten Differenzen bei Zwischenergebnissen auf, die auch null wurden. In solchen Fällen stand in den Texten aber nur,[10] dass Minuend und Subtrahend gleich seien, es findet sich weder ein Name für null noch wurde eine Anzahl von null als Lösung algebraischer Aufgaben anerkannt. Die Babylonier kannten daher noch keine Zahl Null.

Ägypten, Griechenland und Römisches Reich

In Ägypten wurde im 2. Jahrhundert v. Chr. am Horus-Tempel in Edfu eine Inschrift angebracht, in der die Maße von Tempelländereien angegeben sind. Die Ländereien teilte man – so die heutige, jedoch nicht sichere Interpretation – in vier- und dreieckige Parzellen auf, deren Flächen dann nach einer allgemeinen Formel für Vierecke aus den vier Seitenlängen ungefähr berechnet wurden. Bei Dreiecken wurde die vierte Seite null gesetzt und als Zeichen dafür die Hieroglyphe

(„nichts“) benutzt. Die Zahl Null war also vielleicht schon zu dieser Zeit in Ägypten bekannt.[11]

Die Griechen dagegen kannten keine Zahl Null. Erst die hellenistische Welt übernahm von den Babyloniern mit der Astronomie auch deren Sexagesimalbrüche, man schrieb diese jedoch mit den ionischen Zahlsymbolen.[12] So auch der griechische Astronom Klaudios Ptolemaios, der im 2. Jahrhundert n. Chr. in der berühmten Bibliothek des Museions in Alexandria arbeitete. Er verwendete in astronomischen Angaben das Fehlzeichen o,[13] das vermutlich für griechisch οὐδέν ouden („nichts“) steht.[14]

Die römischen Kaiser förderten zwar die Wissenschaften in den ehemals hellenistischen Gebieten ihres Reiches, bedeutende eigene mathematische Leistungen hatten die Römer jedoch nicht vorzuweisen. Für die Null gab es kein Zeichen im Lateinischen.[15]

Indien und Südostasien

Vermutlich beeinflusst durch das babylonische Sexagesimalsystem sowie Astronomie und Kalenderrechnung[16] entstand zwischen 300 v. Chr. und 600 n. Chr. in Indien das dezimale Stellenwertsystem mit 0 und Zahlzeichen für 1, …, 9, die offenbar aus eigenen Zahlzeichen, die es zu indischen Schriften gab, entstanden waren.[17] Da in dezimalen Zahlen Stellen mit einer Lücke, d. h. dem Wert null, sehr viel häufiger auftreten als im babylonischen Sexagesimalsystem, wurde ein Lückenzeichen für die Null im dezimalen Stellenwertsystem unentbehrlich, was für die Akzeptanz der Null als Zahl wohl förderlich gewesen sein dürfte. Nach der 2017 veröffentlichten Radiokarbondatierung findet sich der älteste materielle Beleg für ein schriftliches Symbol der Null im indischen Raum im Bakhshali-Manuskript. Demnach stammten die ältesten Teile des Manuskripts aus dem 3. oder 4. Jahrhundert n. Chr.[18] Die in der Öffentlichkeit dabei verbreitete Interpretation der Ergebnisse der Radiokarbondatierung ist von anderen Forschern wie Kim Plofker in Frage gestellt worden. Nach ihnen zeigt das Manuskript eine Einheitlichkeit sowohl bei Schrift, Inhalt und Erhaltungszustand, die darauf deutet, dass es dem spätesten Zeitpunkt der Datierungen zugeordnet werden sollte.[19]

Seit dem 7. Jahrhundert n. Chr. findet sich in Inschriften ein Punkt oder ein Kreis als Symbol für die „Leere“ („śūnya“), wie in Indien spätestens seit dem 5. Jahrhundert n. Chr. die Null genannt wurde.[20] In seinem 628 n. Chr. verfassten Lehrbuch „Brāhmasphutasiddhānta“ gab der in Bhinmal (Rajasthan) lehrende Mathematiker und Astronom Brahmagupta Rechenregeln auch für die Null an.[21] Ein früher gesicherter Nachweis der Null als Zahl in Indien (schon früher in Südostasien) ist eine Steintafel aus dem Ort Gwalior 500 km südlich von Neu-Delhi mit den Daten 27. Dezember 786, 10. Januar 787 und 17. Januar 787, die von einer Gartenanlage handelt, deren Länge 270 (hastas) beträgt und 50 Blumengirlanden erhielt[22].

Eine weitere frühe schriftliche Verwendung der Null findet sich in der Inschrift K. 151 aus Sambor Prei Kuk in Kambodscha vom Anfang des 7. Jahrhunderts n. Chr. und berichtet von der Errichtung einer Götterstatue am 14. April 598: Das hier benutzte Jahr der Śaka-Ära ist 520, wobei die Null mit dem Begriff „Luftraum“ („kha“) wiedergegeben ist.[23] Ein weiterer Nachweis der Verwendung der Ziffer „0“ stammt ebenfalls aus Kambodscha, und zwar in der Inschrift K. 127, wo in Ziffern das Śakajahr „605“ genannt wird, das unserem Jahr 683/84 entspricht.[24] Eine ganze Reihe von Inschriften, deren Datum „0“ enthält und die aus etwa der gleichen Zeit stammen, wurden auf Sumatra gefunden.[25]

In den ursprünglichen indischen Systemen war die Reihenfolge der Potenzen umgedreht, die Einer wurden zuerst genannt, dann die Zehner etc. Die Ziffer Null erhöhte damit den Wert der folgenden Ziffer.

China

Im antiken China kannte man keine Zahl Null, denn Problemstellungen hatten niemals eine Anzahl von null als Lösung und es gab keine eigenständige Null, mit der man wie mit anderen Zahlen rechnen konnte.[26] Zahlen wurden jedoch wohl spätestens seit dem 1. Jahrhundert n. Chr. (frühe Han-Dynastie) durch Stäbchen ausgelegt (Jiu Zhang Suanshu, Kapitel 8, Problem 3):[27] Die Einer senkrecht, die Zehner waagerecht, die Hunderter wieder senkrecht usw., wobei an einer Stelle mit mehr als 5 Stäbchen 5 davon durch ein Stäbchen in jeweils anderer Richtung ersetzt wurden.[28] Man verfügte also über ein dezimales Stellenwertsystem, in dem es allerdings – wie im ursprünglichen Sexagesimalsystem der Babylonier – kein Fehlzeichen für Stellen ohne Wert gab.[29] Erst in der Übersetzung eines indischen astronomischen Textes aus der Zeit von 713 bis 741 n. Chr. findet sich die früheste bekannte chinesische Erwähnung eines Fehlzeichens (ein Punkt).[30]

Ebenso war wahrscheinlich schon im 1. Jahrhundert n. Chr. eine Art Matrizenrechnung zur Lösung von linearen Gleichungssystemen bekannt (Jiu Zhang Suanshu, Kapitel 8).[31] Dabei traten in den Rechnungen auch negative Werte auf, die man mit Stäbchen – erstmals in der Geschichte – unterschiedlich zu positiven Werten darstellte. Für diese wurden Additions- und Subtraktionsregeln angegeben, insbesondere auch für leere Einträge, die Matrizenelementen mit dem Wert null entsprachen. Damit hatte man eine rechnerische Vorstufe der Zahl Null. Die Vorzeichenregeln der Multiplikation sind in China dagegen erst ab 1299 n. Chr. nachgewiesen.[32]

Europa ab dem Mittelalter

Während weite Teile Westeuropas vor allem im Frühmittelalter unter dem Zerfall des römischen Reiches und anderen Faktoren litten, wurde in Byzanz (Universität von Konstantinopel) und in den jetzt islamisierten Gebieten von Muslimen, Juden und Christen weiterhin Mathematik auf einem hohen Niveau betrieben. Die indischen Ziffern mit ihrem Dezimalsystem werden erstmals vom syrischen Bischof und Gelehrten Severus Sebokht im 7. Jahrhundert beschrieben, und mit dem Werk Über das Rechnen mit indischen Ziffern (um 825) von al-Chwarizmi, einem choresmischen Mathematiker, über ein großes Gebiet verbreitet. Weitere Rechenbücher, wie die von Ibn Ezra im 12. Jahrhundert, folgten.

Leonardo Fibonacci, ein Mathematiker des Mittelalters, der in Algier als Sohn eines italienischen Handelsvertreters mit den arabisch-indischen Zahlen inklusive der Null vertraut war, führte diese 1202 mit seinem Werk Liber abaci, worin er Beispiele aus der Handelswelt bearbeitete, in Italien ein. Er räumt der Null aber nicht den gleichen Stellenwert wie den übrigen Zahlen ein – in seinem Buch nennt er sie Zeichen statt Zahl. Die Verwendung der Null im praktischen Rechnen setzte sich aber erst viel später (im 17. Jahrhundert) durch. Noch Gerolamo Cardano im 16. Jahrhundert kam ohne sie aus.[33]

Für die Ziffer und die “neue Zahl” 0 gibt es in vielen europäischen Sprachen eine vom deutschen Wort „null“ abweichende Benennung; zu diesen Unterschieden siehe unten bei Herkunft des Wortes.

In den folgenden Jahrhunderten gewann die Null in vielen Bereichen an Bedeutung. Die Null wurde zum Ausgangspunkt für viele Skalen, z. B. bei Temperatur oder Meeresspiegel, und so wuchsen die Begriffe „positiv“ und „negativ“ im Denken der Menschen.

Fälschlicherweise wird auch immer wieder behauptet, dass es Papst Silvester II. (mit bürgerlichem Namen Gerbert von Aurillac) gewesen sei, der die arabisch-indischen Zahlen nach Europa gebracht hätte.

Neue Welt

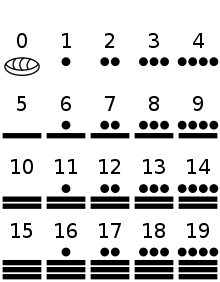
Die Zahlensymbole der Maya. Die Ziffer Null wurde mit einem Zeichen dargestellt, das einer Muschel oder einem Schneckenhaus ähnelt.

Olmeken und Maya

Die Olmeken entwickelten als erstes Volk in Mesoamerika eine erste Form eines astronomischen Kalenders. Das früheste Datum in diesem Kalender, das bislang entdeckt wurde, lautet 7.16.6.16.18 und entspricht wahrscheinlich einem Tag im September 32 v. Chr. (Lange Zählung). Auch die Maya hatten einen solchen Kalender, aus dem sie eine reine Zahlendarstellung im Vigesimalsystem (Stellenwertsystem zur Basis 20) entwickelten. Dabei wurden Stellen mit dem Wert null durch eine Muschel oder ein Schneckenhaus symbolisiert. Das älteste bisher gefundene Datum zeigt einen Tag im Jahr 36 v. Chr.

Inka

Für das Volk der Inka ist ein dezimales Stellenwertsystem nachgewiesen: Sie verwendeten die Knotenschrift der Quipus, die auf einem solchen System aufgebaut war. Als Fehlzeichen diente dabei am Faden eine Stelle ohne Knoten.

Symbole und Schreibweisen

Die indische Ziffer 0

Sofern Verwechslungsgefahr mit dem großen lateinischen Buchstaben O besteht, wird die Ziffer 0 mit einem Schrägstrich oder Punkt gekennzeichnet, z. B.: $0\!\!\!{/}$ oder 0̷ oder $0\!\!{\cdot }$ .

In der Mathematik steht das Symbol „0“ häufig auch allgemein für Nullelemente von Strukturen, selbst wenn diese von einer Zahl 0 unterschieden werden.

Andere Zahlschriften

Chinesische Null

Die Null im Stellenwertsystem

Eine einzeln stehende Ziffer 0 bezeichnet die Zahl Null, ansonsten bedeutet eine Ziffer 0 an einer Stelle, dass der zugehörige Stellenwert in der Stellenwertdarstellung einer Zahl nicht auftritt, z. B. „307“ für 3·100 + 0·10 + 7·1. Wenn die Ziffer 0 an eine Ziffernfolge angehängt wird, multipliziert sich deren Wert mit der Basis des Stellenwertsystems.

Führende Nullen werden üblicherweise weggelassen bzw. bei einer formatierten Ausgabe durch Leerzeichen ersetzt.

Bei Dezimalzahlen werden Nullen nach dem Komma üblicherweise weggelassen, wenn ihnen keine andere Ziffer mehr folgt. Bei einer formatierten Ausgabe werden sie entsprechend dem Ausgabeformat geschrieben. Eine Ausnahme bilden die Angaben von Messwerten. Hier wird die Null oft zusätzlich geschrieben, um die Genauigkeit der Messung zu veranschaulichen.

Beispiel: Eine Länge wird mit 1,200 m gemessen. Die zwei zusätzlichen Nullen zeigen hier, dass die Messung auf drei Stellen hinter dem Komma genau war.

Typenangaben erfolgen oft mit führender Null, z. B. 001. Auch bei Nummerierungen, wie Bestellnummern, Rechnungsnummern, Ausweisnummern und so weiter, deren Ziffernfolge auf eine bestimmte Anzahl von Stellen festgelegt ist, werden nicht genutzte Stellen am Anfang mit führenden Nullen aufgefüllt.

Arithmetische Eigenschaften

Die Zahl Null weist einige besondere Eigenschaften auf, die bei der Untersuchung von Rechenregeln hervortreten.

Addition

Die Null symbolisiert im mathematischen Sinne das neutrale Element der Addition in einem kommutativen Monoid, das heißt: Für jedes Element a des Monoids gilt

a+0=a=0+a

.

Die Null im mathematischen Sinne (als neutrales Element eines Monoids) ist stets eindeutig.

Subtraktion

Die Null entsteht als Resultat einer Differenz, bei der der Subtrahend gleich dem Minuenden ist

a-a=0

.

Ferner ist

a-0=a

und

0-a=-a

.

Multiplikation

Durch Einführung der Rechenoperation der Multiplikation, mathematisch formal in der Definition eines Ringes, erhält man folgende Regel:

a\cdot 0=0=0\cdot a

.

Man sagt auch, die Null ist ein absorbierendes Element der Multiplikation.

Division

Das Ergebnis der Division von null durch eine von null verschiedene Zahl ist stets null. Das Ergebnis null tritt nur auf, wenn der Dividend null ist.

Jede mögliche Definition der Division einer Zahl durch null verstößt gegen das Permanenzprinzip. Deshalb ist es in aller Regel zweckmäßig, solche Division undefiniert zu lassen.

Für natürliche Zahlen kann die Division als wiederholte Subtraktion angesehen werden:
Um die Frage „Wie oft muss man 4 von 12 abziehen, um 0 zu erhalten?“ zu beantworten, also 12 : 4 zu bestimmen, kann man so rechnen:

12-4=8

8-4=4

4-4=0

Die Anzahl der Subtraktionen ist 3.

Also ist

12:4=3

Bei $12:0$ lautet die Frage: „Wie oft muss man 0 von 12 abziehen, um 0 zu erhalten?“ Antwort: Keine Anzahl von Operationen bringt das gewünschte Ergebnis.

Anmerkung: Bei $0:0$ lautet die Frage: „Wie oft muss man 0 von 0 abziehen, um 0 zu erhalten?“ Antwort: Jede beliebige (also keine eindeutige) Anzahl von Operationen bringt das gewünschte Ergebnis.

Für beliebige Zahlenmengen ist die Division als Umkehrung der Multiplikation definiert. Bei der Division von b durch a sucht man eine Zahl x, welche die Gleichung $a\cdot x=b$ erfüllt. Diese Zahl x – sofern sie eindeutig bestimmt ist – schreibt man als Quotienten $x={\frac {b}{a}}$

Im besonderen Fall, dass $a=0$ ist, gibt es kein eindeutiges Ergebnis: Wir suchen eine Lösung der Gleichung $0\cdot x=b$ .

Im Fall $b\neq 0$ ist die Gleichung unlösbar, weil es keine Zahl x gibt, für die $0\cdot x\neq 0$ gilt.
Im Fall $b=0$ wird die Frage, welche Zahl x die Gleichung erfüllt, trivial: Jede Zahl x erfüllt die Gleichung $0\cdot x=0$ .

Also gibt es in beiden Fällen kein eindeutiges Ergebnis bei der Division durch null.

Beim Rechnen mit reellen (oder komplexen) Zahlen ist es also nicht möglich, durch null zu dividieren, da diese Operation kein eindeutiges Ergebnis hätte: Die Multiplikation mit 0 ist nicht umkehrbar. Dies gilt allgemein für jeden Ring.

Historische Ansichten

Für Leonhard Euler war die Division von $1:0=\infty$ (Unendlich). Entsprechend nahm er an, dass es verschieden große unendliche Zahlen gab, denn z. B. $2:0$ würde (so Euler) eine doppelt so große unendliche Zahl wie $1:0$ ergeben.[34]

Auch bei den Indern blieb das Problem der Division durch null ungelöst. Brahmagupta kam zu keinem Ergebnis, verbot die Division durch null aber auch nicht[35], während Bhaskara im 12. Jahrhundert wie Euler auf das Ergebnis unendlich kam.

Potenzrechnung

Für $b>0$ ist $0^{b}=0$ . Für $b<0$ ist $0^{b}$ nicht definiert.

Per Definition gilt $a^{0}=1$ , für $a\neq 0$ . Der Ausdruck $0^{0}$ wird entweder undefiniert gelassen oder – sofern dies zweckmäßiger ist – als 1 definiert. Siehe Potenz.

Auftreten in der Algebra

In Restklassenringen (aber nicht nur dort) existieren sogenannte Nullteiler, zum Beispiel gilt im Restklassenring modulo 6 die Gleichung 2 · 3 = 0. Daraus folgt jedoch nicht, dass 0 / 2 = 3 ist, denn auch 2 · 0 = 0. Man kann also diesen Quotienten nicht eindeutig (und damit sinnvoll) definieren und daher auch nicht durch einen Nullteiler dividieren. Mit 0 wird auch das neutrale Element einer beliebigen (additiven) Gruppe, beispielsweise Nullvektoren und Nullmatrizen, bezeichnet.

Bedeutung in der Informatik

In vielen Programmiersprachen und Programmbibliotheken hat das erste Element eines ordinalen Datentypen die Ordnungszahl 0. Dies kann zum Off-by-one-Error führen.
In Anlehnung an die Zahl Null ist in der Informatik die Rede von Nullwerten, diese sind jedoch im Allgemeinen nicht mit der Zahl Null zu identifizieren. Häufig ist damit gemeint, dass ein Wert nicht definiert, also ein Datenfeld nicht belegt wurde.

Vorzeichenbehaftete Null

Bei Maschinenzahlen werden manchmal die positive (+0) und die negative Null (−0) als zwei verschiedene Zahlen angesehen. Beim Datentyp Integer ist die Null in der Betrags-Vorzeichendarstellung und beim Einerkomplement vorzeichenbehaftet, bei Gleitkommazahlen ist es meistens der Fall. Die Norm IEEE 754 für binäre Gleitkommazahlen verlangt neben Existenz einer positiven und der negativen Null drei gesondert kodierte Werte namens NaN, +Inf und −Inf (infinity = Unendlichkeit). Während die beiden Darstellungen der Null nach IEEE 754 identisch bei numerischen Vergleichen sind, bewirken sie unterschiedliche Ergebnisse bei einigen Berechnungen und haben unterschiedliche Bitmuster.

Division durch null auf Computern

Für Computer muss speziell definiert werden, wie sich ein Prozessor oder Programm im Falle einer Division durch null verhalten soll (das heißt, wie die Semantik des Divisionsbefehls lautet). Hersteller und Entwickler sind dabei prinzipiell frei in ihren Entscheidungen, daher gibt es keine allgemeingültige Definition für sämtliche Prozessoren und Programme. Jedoch gibt es übliche bzw. oft angewandte Definitionen, die im Folgenden dargestellt werden.

Man unterscheidet üblicherweise zwischen ganzzahliger und Gleitkommadivision. Für ganze Zahlen ist es gängig, einen Laufzeitfehler auszulösen, falls ein Programm versucht, durch null zu dividieren. Für Gleitkommazahlen ist nach IEEE 754 eine Division durch null definiert, da dort gesondert kodierte Werte für $\pm \infty$ spezifiziert sind. Allerdings ist die Division $\pm 0/\pm 0$ numerisch unbestimmt und ergibt NaN (not a number).

In der Mathematik werden solche Werte im Allgemeinen nicht verwendet, da durch diese gewünschte Eigenschaften des Zahlenraums (etwa der reellen Zahlen) wie etwa das Distributivgesetz nicht mehr anwendbar wären. Etwa in der Analysis wird ∞ nicht als Zahl, sondern lediglich symbolisch verwendet, etwa um Grenzwerte oder bestimmte Divergenz zu notieren. Diese Herangehensweise entspricht der Verwendung bei der Berechnung von Grenzwerten in der reellen Analysis, das direkte Auftreten etwa einer Division durch null wird jedoch auch formal vermieden, da ansonsten die Anwendung gewisser Rechengesetze zu Widersprüchen führt.

Sprachgebrauch

Die Formulierung „null Uhr“ bedeutet Mitternacht (nicht zu verwechseln mit der Stunde Null, einer Metapher für den Beginn der Nachkriegszeit in Deutschland.).
Es wird unterschieden zwischen „24:00 Uhr“ und „00:00 Uhr“. Dabei kommt es darauf an, ob der Tag endet (24:00 Uhr) oder ob der Tag beginnt (00:00 Uhr). So ist z. B. Montag 24:00 Uhr derselbe Zeitpunkt wie Dienstag 00:00 Uhr. Fahrpläne bezeichnen Mitternacht als Ankunftszeit mit 24:00 Uhr und als Abfahrtzeit mit 00:00 Uhr.
Das Wort „null“ kommt auch in zahlreichen Redensarten vor (zum Beispiel jemanden auf null bringen, etwas bei null anfangen, jemand sei fachlich gesehen eine Null).
Ebenso wird der Beginn unserer Zeitrechnung häufig als „Jahr null“ bezeichnet, obwohl es dieses nicht gab.
Nullnummer oder Dummy (engl. für Attrappe), Ausgabe einer Zeitschrift oder Zeitung, die vor der eigentlichen Neueinführung des Mediums erscheint

Herkunft des Wortes

Mit der Einführung der Ziffer 0, die zugleich einen Zahlwert darstellte, musste für diese 0 eine Benennung gefunden werden, im Deutschen ist es null, in anderen Sprachen zero/zéro. Die Entwicklung in den modernen europäischen Sprachen war folgende: Im Italienischen bildete sich – vom Arabischen entlehnt – das Wort zero, das wurde dann im Französischen und schließlich Englischen gebräuchlich. „Null“ hat im Englischen – und in der Informatik – eine von 0 zu unterscheidende Bedeutung, siehe Nullwert.

Die heutige deutsche Bezeichnung stammt vom lateinischen Wort nullus (= keiner) bzw. altitalienisch nulla figura (= keine Ziffer). Die ursprüngliche Bedeutung von null im Deutschen steckt noch in der Wendung null und nichtig = ungültig (ohne Wert), dies ist eine Doppelung, auch null bedeutet hier „nichtig“.

Literatur

Helmuth Gericke: Geschichte des Zahlbegriffs. Bibliographisches Institut, Mannheim 1970.
Helmuth Gericke: Mathematik in Antike und Orient. Springer, Berlin u. a. 1984
Georges Ifrah: Universalgeschichte der Zahlen. Campus, Frankfurt 1986. ISBN 3-593-34192-1.
George Joseph: The Crest of the Peacock – the non european roots of mathematics, London 1991
Robert Kaplan: Die Geschichte der Null. Gebundene Ausgabe: Campus Verlag, Frankfurt/M. 2000, ISBN 3-593-36427-1. Taschenbuchausgabe: Piper, 2003, ISBN 3-492-23918-8 (englisches Original 1991).
Jean-Claude Martzloff: A History of Chinese Mathematics. Springer, Berlin u. a. 1997
Karl Menninger: Zahlwort und Ziffer: Eine Kulturgeschichte der Zahl. 3. Aufl., Vandenhoeck & Ruprecht, Göttingen 1979
Mukherjee: Discovery of Zero and its impact on indian mathematics, Calcutta 1991
Brian Rotman: Die Null und das Nichts. Eine Semiotik des Nullpunkts. Aus dem Englischen von Petra Sonnenfeld. Kulturverlag Kadmos, Berlin 2000, ISBN 978-3-931659-17-2.
Charles Seife: Zwilling der Unendlichkeit: Eine Biographie der Zahl Null. München 2002. ISBN 3-442-15054-X.
Klaus Sturm (Hrsg.): Diagonal. Nr. 0. Siegen, o. J. ISSN 0938-7161 (Null-Nummer der Zeitschrift Diagonal mit zahlreichen Beiträgen zum Thema „Null“.)
Kurt Vogel: Vorgriechische Mathematik II: Die Mathematik der Babylonier. Schroedel, Hannover und Schöningh, Paderborn 1959

Weblinks

Wiktionary: null – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikiquote: Null – Zitate

Commons: Null – Sammlung von Bildern, Videos und Audiodateien

Fußnoten

bei einigen Streitkräften, beispielsweise in der Bundeswehr, erfolgt die Darstellung mit einem kleinen Schrägstrich oben rechts, vgl. File:Bundeswehr - ATN Sicherungssoldat 1994 (links) mit Umrandung "ATN 3002987".jpg
in der Gebärdensprache:
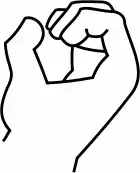
in Darstellungen von Computermonitoren oder - Ausdrucken: teils mit Punkt (mittig) oder mit Schrägstrich:
Vogel; S. 16, Fußnote 3.
Bei dieser Wiedergabe sexagesimaler Zahlen werden die Stellen durch Kommas voneinander getrennt.
Gericke: Geschichte des Zahlbegriffs. S. 46 f.
Vogel; S. 17.
Menninger; Bd. 1, S. 178, Bd. 2, S. 212.
Vogel; S. 60 f.
Vogel; S. 61.
Gericke: Mathematik in Antike und Orient. S. 58–60.
siehe E. Löffler: Ziffern und Ziffernsysteme. 1. Teil: Die Zahlzeichen der alten Kulturvölker. 2., neu bearb. Aufl., B.G. Teubner, Leipzig–Berlin 1918; S. 37 f.
H.-D. Ebbinghaus et al.: Zahlen. 3. Aufl., Springer, Berlin 1992; S. 12.
Menninger; Bd. 2, S. 212 f.
Wie konnte man die römischen Zahlen entziffern?. WAS IST WAS. Abgerufen am 13. Mai 2016.
Ergebnisse der babylonischen Astronomie gelangten vom 3. Jahrhundert v. Chr. bis zum 1. Jahrhundert n. Chr. vor allem über den Hafen Bharukaccha in Nordwestindien ins Land und damit auch Kenntnisse über das babylonische Sexagesimalsystem. Neugebauer: A history of ancient mathematical astronomy. 1975. Ifrah loc. cit.; S. 508.
Gericke: Mathematik in Antike und Orient. S. 184 ff.
Hannah Devlin: Much ado about nothing: ancient Indian text contains earliest zero symbol. The Guardian, 14. September 2017, abgerufen am 14. September 2017 (englisch). Carbon dating finds Bakhshali manuscript contains oldest recorded origins of the symbol 'zero'. Bodleian Library, 14. September 2017, abgerufen am 14. September 2017 (englisch).
Kim Plofker, Agathe Keller, Takao Hayashi, Clemency Montelle, Dominik Wujastyk: „The Bakhshālī Manuscript: A Response to the Bodleian Library’s Radiocarbon Dating“, in: History of Science in South Asia 5.1 (2017), S. 134–150. doi:10.18732/H2XT07.
Gericke: Geschichte des Zahlbegriffs. S. 47.
Gericke: Mathematik in Antike und Orient. S. 189, 192.
Epigraphia Indica, Vol. I, Calcutta 1892, S. 159–162.
K.-H. Golzio, Chronologie der Inschriften Kambojas, Wiesbaden 2006, S. 1.
Golzio: Chronologie. S. 23.
G. Cœdès: Les inscriptions malaises de Çrīvijaya. BEFEO XXX, 1930, S. 29–80; auf S. 33–44.
Martzloff; S. 204.
Martzloff; S. 210
Gericke: Mathematik in Antike und Orient. S. 170. Für die Nutzung von Rechenbrettern in der frühen Han-Zeit gibt es keinen Beweis: Martzloff; S. 209.
Anders als von einigen Historikern behauptet, lassen sich für die Zeit vor dem 8. Jahrhundert n. Chr. keine Lücken für fehlende Stellen nachweisen: Martzloff; S. 204–207.
Martzloff; S. 207.
Gericke: Mathematik in Antike und Orient. S. 176–177. Zur Unsicherheit der Datierung siehe Martzloff; S. 131.
Martzloff; S. 200–203.
MacTutor Webseite, loc. cit.
Euler: Vollständige Anleitung zur Algebra. St. Petersburg 1802, Bd. 1, S. 49.
John J. O’Connor, Edmund F. Robertson: Brahmagupta. In: MacTutor History of Mathematics archive.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Streitkräften, beispielsweise in der Bundeswehr, erfolgt die Darstellung mit einem kleinen Schrägstrich oben rechts, vgl. File:Bundeswehr - ATN Sicherungssoldat 1994 (links) mit Umrandung "ATN 3002987".jpg

[2] r Gebärdensprache:

[3] Darstellungen von Computermonitoren oder - Ausdrucken: teils mit Punkt (mittig) oder mit Schrägstrich:

[4] Vogel; S. 16, Fußnote 3.

[5] Bei dieser Wiedergabe sexagesimaler Zahlen werden die Stellen durch Kommas voneinander getrennt.

[6] Gericke: Geschichte des Zahlbegriffs. S. 46 f.

[7] Vogel; S. 17.

[8] Menninger; Bd. 1, S. 178, Bd. 2, S. 212.

[9] Vogel; S. 60 f.

[10] Vogel; S. 61.

[11] Gericke: Mathematik in Antike und Orient. S. 58–60.

[12] siehe E. Löffler: Ziffern und Ziffernsysteme. 1. Teil: Die Zahlzeichen der alten Kulturvölker. 2., neu bearb. Aufl., B.G. Teubner, Leipzig–Berlin 1918; S. 37 f.

[13] H.-D. Ebbinghaus et al.: Zahlen. 3. Aufl., Springer, Berlin 1992; S. 12.

[14] Menninger; Bd. 2, S. 212 f.

[15] Wie konnte man die römischen Zahlen entziffern?. WAS IST WAS. Abgerufen am 13. Mai 2016.

[16] Ergebnisse der babylonischen Astronomie gelangten vom 3. Jahrhundert v. Chr. bis zum 1. Jahrhundert n. Chr. vor allem über den Hafen Bharukaccha in Nordwestindien ins Land und damit auch Kenntnisse über das babylonische Sexagesimalsystem. Neugebauer: A history of ancient mathematical astronomy. 1975. Ifrah loc. cit.; S. 508.

[17] Gericke: Mathematik in Antike und Orient. S. 184 ff.

[18] Hannah Devlin: Much ado about nothing: ancient Indian text contains earliest zero symbol. The Guardian, 14. September 2017, abgerufen am 14. September 2017 (englisch). Carbon dating finds Bakhshali manuscript contains oldest recorded origins of the symbol 'zero'. Bodleian Library, 14. September 2017, abgerufen am 14. September 2017 (englisch).

[19] Kim Plofker, Agathe Keller, Takao Hayashi, Clemency Montelle, Dominik Wujastyk: „The Bakhshālī Manuscript: A Response to the Bodleian Library’s Radiocarbon Dating“, in: History of Science in South Asia 5.1 (2017), S. 134–150. doi:10.18732/H2XT07.

[20] Gericke: Geschichte des Zahlbegriffs. S. 47.

[21] Gericke: Mathematik in Antike und Orient. S. 189, 192.

[22] Epigraphia Indica, Vol. I, Calcutta 1892, S. 159–162.

[23] K.-H. Golzio, Chronologie der Inschriften Kambojas, Wiesbaden 2006, S. 1.

[24] Golzio: Chronologie. S. 23.

[25] G. Cœdès: Les inscriptions malaises de Çrīvijaya. BEFEO XXX, 1930, S. 29–80; auf S. 33–44.

[26] Martzloff; S. 204.

[27] Martzloff; S. 210

[28] Gericke: Mathematik in Antike und Orient. S. 170. Für die Nutzung von Rechenbrettern in der frühen Han-Zeit gibt es keinen Beweis: Martzloff; S. 209.

[29] Anders als von einigen Historikern behauptet, lassen sich für die Zeit vor dem 8. Jahrhundert n. Chr. keine Lücken für fehlende Stellen nachweisen: Martzloff; S. 204–207.

[30] Martzloff; S. 207.

[31] Gericke: Mathematik in Antike und Orient. S. 176–177. Zur Unsicherheit der Datierung siehe Martzloff; S. 131.

[32] Martzloff; S. 200–203.

[33] MacTutor Webseite, loc. cit.

[34] Euler: Vollständige Anleitung zur Algebra. St. Petersburg 1802, Bd. 1, S. 49.

[35] John J. O’Connor, Edmund F. Robertson: Brahmagupta. In: MacTutor History of Mathematics archive.