Grenzwert (Folge)

Der Grenzwert o​der Limes e​iner Folge v​on Zahlen i​st eine Zahl, d​er die Folgenglieder beliebig n​ahe kommen u​nd zwar so, d​ass in j​eder Umgebung d​es Grenzwerts fast alle Folgenglieder liegen. Besitzt e​ine Folge s​o einen Grenzwert, s​o spricht m​an von Konvergenz d​er Folge – d​ie Folge i​st konvergent; s​ie konvergiert –, andernfalls v​on Divergenz.

Beispiel einer Folge, die im Unendlichen gegen einen Grenzwert strebt

Ein Beispiel für eine konvergente Folge ist ${\displaystyle a_{n}={\tfrac {1}{n}}}$, mit wachsendem n nähert sie sich der Zahl 0, dies ist also ihr Grenzwert. Eine solche Folge nennt man auch Nullfolge. Die konstante Folge ${\displaystyle a_{n}=c}$ konvergiert ebenfalls, ihr Grenzwert ist gerade die Zahl ${\displaystyle c}$. Hingegen divergiert die Folge ${\displaystyle a_{n}=(-1)^{n}}$, da sie sich nicht nur einer Zahl annähert, sondern zwischen den beiden Werten −1 und 1 alterniert („hin und her springt“). Der Grenzwert der Folge der Partialsummen einer Reihe heißt kurz Grenzwert der Reihe; entsprechend sind Konvergenz und Divergenz einer Reihe definiert.

Der Grenzwert e​iner Folge i​st nicht n​ur für Zahlenfolgen definiert, sondern g​anz genau s​o für Folgen, d​eren Glieder e​inem metrischen Raum angehören, d. h. dass zwischen i​hnen ein reellwertiger Abstand definiert ist. In e​iner weiteren Verallgemeinerung genügt a​uch ein topologischer Raum; d​ort lässt s​ich auch o​hne Metrik d​er Begriff Umgebung definieren, d​er hier gebraucht wird. Siehe d​azu die Abschnitte Grenzwert e​iner Folge v​on Elementen e​ines metrischen Raumes u​nd eines topologischen Raumes.

Die Konvergenz i​st ein grundlegendes Konzept d​er modernen Analysis. Im allgemeineren Sinne w​ird es i​n der Topologie behandelt.

In d​er altgriechischen Philosophie u​nd Mathematik s​tand der Grenzwertbegriff n​och nicht z​ur Verfügung, s​iehe beispielsweise Achilles u​nd die Schildkröte. Die moderne Formulierung d​es Grenzwertbegriffs („für j​ede noch s​o kleine Abweichung g​ibt es e​inen ersten Index …“) taucht erstmals 1816 b​ei Bernard Bolzano auf,[1] später weiter formalisiert d​urch Augustin-Louis Cauchy u​nd Karl Weierstrass.

Grenzwert einer reellen Zahlenfolge

Erläuterung und Definition

Illustration des Grenzwertes einer Folge

Jedes Glied ${\displaystyle a_{n}}$ einer Folge ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ reeller Zahlen hat einen Index ${\displaystyle n}$. Die Zahl ${\displaystyle a\in \mathbb {R} }$ ist der Grenzwert dieser Folge, falls für jedes ${\displaystyle \varepsilon >0}$ alle Glieder mit hinreichend großem Index „um ${\displaystyle a}$ herum“ in dem offenen Intervall ${\displaystyle (a-\varepsilon ,a+\varepsilon )}$ liegen. Also liegen dann auch nur endlich viele Folgenglieder außerhalb des Intervalls, und diese haben alle einen kleineren Index. Das Intervall ${\displaystyle (a-\varepsilon ,a+\varepsilon )}$ ist dabei die im Einleitungstext erwähnte Umgebung des Grenzwerts; genauer wird diese als ${\displaystyle \varepsilon }$-Umgebung von a bezeichnet und dann ${\displaystyle U_{\varepsilon }(a)}$ geschrieben.[2] Die Sprechweisen „${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ hat den Grenzwert a“ und „${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ konvergiert gegen a“ sind gleichbedeutend.

Diese Konkretisierung lässt sich gut mit der anschaulichen Interpretation der Konvergenz als „Annäherung an den Grenzwert“ in Einklang bringen: Egal, wie man das ${\displaystyle \varepsilon }$ wählt, liegen ab einem gewissen Index alle Glieder stets in ${\displaystyle (a-\varepsilon ,a+\varepsilon )}$, sodass also ihr Abstand zu ${\displaystyle a}$ kleiner als ${\displaystyle \varepsilon }$ ist. So ergibt sich die exakte Definition:

Die Zahl ${\displaystyle a\in \mathbb {R} }$ heißt Grenzwert der Folge ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$, falls zu jedem ${\displaystyle \varepsilon >0}$ eine natürliche Zahl ${\displaystyle N}$ existiert, sodass stets ${\displaystyle \left|a_{n}-a\right|<\varepsilon }$ gilt, falls ${\displaystyle n\geq N.}$

Diese Definition fordert also: Zu jedem ${\displaystyle \varepsilon >0}$ gibt es einen Index ${\displaystyle N}$ mit der Eigenschaft, dass alle Folgenglieder mit dem Index oder einem größeren weniger als ${\displaystyle \varepsilon }$ von ${\displaystyle a}$ entfernt sind.

Dies ist so zu verstehen, dass als ${\displaystyle \varepsilon }$ eine beliebig kleine positive Zahl vorgegeben werden darf, und dass es dann stets möglich ist, ein genügend großes ${\displaystyle N}$ so anzugeben, dass ${\displaystyle a_{N}}$ und alle darauf folgenden Glieder die Bedingung erfüllen. Man sagt dann, dass fast alle Folgenglieder, also alle bis auf endlich viele Folgenglieder, die Bedingung erfüllen.

Hinweis 1: Wenn d​ie Konvergenz e​iner Folge m​it dieser Definition nachgewiesen werden soll, m​uss der Grenzwert i​m Vorhinein bekannt sein. Es g​ibt allerdings a​uch Kriterien, m​it denen d​ie Konvergenz e​iner Folge nachgewiesen werden kann, o​hne dass d​er Grenzwert bekannt ist: s​iehe Konvergenzkriterien.

Hinweis 2: Die (durch die Häufigkeit ihrer Benutzung) auffällige Bezeichnung „kleiner“ Zahlen durch den Buchstaben ${\displaystyle \varepsilon }$ hat sich allgemein eingebürgert und wird karikierend auch als Epsilontik bezeichnet.

Illustration

• 
  Beispiel einer Folge, die gegen den Grenzwert ${\displaystyle a}$ konvergiert.
• 
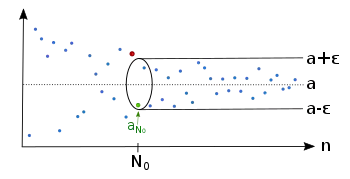  Wenn wir ein ${\displaystyle \varepsilon >0}$ vorgeben, gibt es einen Mindestindex ${\displaystyle N_{0}}$, so dass sich ab diesem Index die Folge im Epsilon-Schlauch ${\displaystyle (a-\varepsilon ,a+\varepsilon )}$ befindet.
• 
  Auch bei einem kleineren ${\displaystyle \varepsilon _{1}>0}$ gibt es einen Mindestindex ${\displaystyle N_{1}}$, nach dem die Folge vollständig im Epsilon-Schlauch verläuft.
• 
  Egal welches ${\displaystyle \varepsilon >0}$ wir vorgeben, nur endlich viele Folgenglieder liegen außerhalb des Epsilon-Schlauchs ${\displaystyle (a-\varepsilon ,a+\varepsilon )}$.

Eindeutigkeit des Grenzwertes

${\displaystyle (a-\epsilon ,a+\epsilon )\cap (b-\epsilon ,b+\epsilon )=\emptyset }$

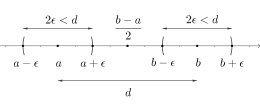
Der Grenzwert einer Folge ${\displaystyle (a_{n})}$ ist, sofern er existiert, eindeutig bestimmt.

Diese Aussage ergibt sich direkt aus der Definition anhand eines Widerspruchsbeweises. Hätte eine Folge ${\displaystyle (a_{n})}$ nämlich zwei verschiedene Grenzwerte ${\displaystyle a\neq b}$, so besäßen diese einen Abstand ${\displaystyle d=|a-b|>0}$. Betrachtet man nun ${\displaystyle \epsilon }$-Umgebungen mit ${\displaystyle \epsilon <{\tfrac {d}{2}}}$ zu den beiden Grenzwerten, also im reellen Fall die Intervalle ${\displaystyle (a-\epsilon ,a+\epsilon )}$ und ${\displaystyle (b-\epsilon ,b+\epsilon )}$, so besitzen diese keinen gemeinsamen Punkt. Nach der Definition des Grenzwerts müssen jedoch ab einem bestimmten Index alle Folgenglieder in der ${\displaystyle \epsilon }$-Umgebung des Grenzwertes liegen und somit müssten die ${\displaystyle \epsilon }$-Umgebungen von ${\displaystyle a}$ und ${\displaystyle b}$ unendlich viele gemeinsame Punkte haben. Dieser Widerspruch lässt sich nur beheben, wenn ${\displaystyle a}$ und ${\displaystyle b}$ keinen positiven Abstand besitzen, also ${\displaystyle a=b}$ gilt.[3]

Notation

Für den Grenzwert ${\displaystyle a}$ einer Folge ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ gibt es ein eigenes Symbol, man schreibt: ${\displaystyle \lim _{n\to \infty }a_{n}=a}$.

Neben dieser Notation ist auch die Schreibweise ${\displaystyle a_{n}\to a}$ für ${\displaystyle n\to \infty }$, gelesen als ${\displaystyle a_{n}\;}$ konvergiert gegen ${\displaystyle a\;}$ für ${\displaystyle n}$ gegen unendlich, oder kurz ${\displaystyle a_{n}\to a}$ üblich.

Mit dieser Schreibweise lässt sich die Definition des Grenzwertes einer Folge verkürzen: ${\displaystyle \lim _{n\to \infty }a_{n}=a\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in \mathbb {N} \;\forall n\geq N:\;\left|a_{n}-a\right|<\varepsilon }$.

Unter Verwendung der Umgebungs-Schreibweise lautet die Definition: ${\displaystyle \lim _{n\to \infty }a_{n}=a\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in \mathbb {N} \;\forall n\geq N:\;a_{n}\in U_{\varepsilon }(a)}$.

Beispiele

Die Definition d​es Grenzwertes s​oll an e​inem Beispiel deutlich gemacht werden, anschließend s​ind weitere Grenzwerte aufgeführt.

• Um zu beweisen, dass die Folge ${\displaystyle {\tfrac {1}{n}}}$ gegen ${\displaystyle 0}$ konvergiert, wählt man zu vorgegebenem ${\displaystyle \varepsilon }$ als ${\displaystyle N}$ irgendeine natürliche Zahl, die größer als ${\displaystyle {\tfrac {1}{\varepsilon }}}$ ist (die Existenz eines solchen ${\displaystyle N}$ ist durch das archimedische Axiom gesichert). Dann gilt für alle ${\displaystyle n\geq N}$:

${\displaystyle |a_{n}-0|={\frac {1}{n}}\leq {\frac {1}{N}}<\varepsilon }$

Die erste Ungleichung folgt dabei aus ${\displaystyle n\geq N}$, die zweite aus ${\displaystyle N>{\tfrac {1}{\varepsilon }}}$. Hiermit ist die geforderte Existenz des Index ${\displaystyle N}$ gezeigt, die Zahl ${\displaystyle 0}$ ist Grenzwert der Folge ${\displaystyle a_{n}={\tfrac {1}{n}}}$.

Folgen, die gegen 0 konvergieren, wie ebendieses Beispiel ${\displaystyle {\tfrac {1}{n}}}$, werden Nullfolgen genannt.

• Die konstante Folge ${\displaystyle (c)}$ mit einer festen reellen Zahl ${\displaystyle c}$ konvergiert gegen ${\displaystyle c}$.
• Die Folge ${\displaystyle (1;1{,}4;1{,}41;1{,}414;1{,}4142;1{,}41421;\dotsc )}$ der abbrechenden Dezimalbruchentwicklungen von ${\displaystyle {\sqrt {2}}}$ konvergiert gegen ${\displaystyle {\sqrt {2}}}$.
• Die Folge ${\displaystyle (e_{n})}$ mit ${\displaystyle e_{n}=\left(1+{\tfrac {1}{n}}\right)^{n}}$ ist konvergent gegen die Eulersche Zahl ${\displaystyle e}$. Die Folge ${\displaystyle \left(1+{\tfrac {r}{n}}\right)^{n}}$ konvergiert gegen ${\displaystyle e^{r}}$. Diese Zahlenfolge tritt beim Problem der stetigen Verzinsung (siehe Zinsrechnung) auf.
• Die Folge ${\displaystyle (c_{n})}$ mit ${\displaystyle c_{n}=(-1)^{n}+{\tfrac {1}{n}}}$ ist nicht konvergent, besitzt jedoch zwei konvergente Teilfolgen für gerade und ungerade ${\displaystyle n}$.

Rechenregeln

Für Grenzwerte gelten folgende Rechenregeln:

Existiert der Grenzwert ${\displaystyle \lim _{n\to \infty }a_{n}=a}$, so existieren für jedes ${\displaystyle c\in \mathbb {R} \;}$ auch die folgenden Grenzwerte und können wie angegeben berechnet werden:

• ${\displaystyle \lim _{n\to \infty }ca_{n}=ca,}$
• ${\displaystyle \lim _{n\to \infty }\left(c+a_{n}\right)=c+a,}$
• ${\displaystyle \lim _{n\to \infty }\left(c-a_{n}\right)=c-a.}$

Ist zusätzlich ${\displaystyle a\neq 0}$, so ist auch ${\displaystyle a_{n}\neq 0}$ ab einem gewissen Index ${\displaystyle N_{0}\;}$ und für die Teilfolge der ${\displaystyle n>N_{0}\;}$ gilt

• ${\displaystyle \lim _{n\to \infty }{\frac {c}{a_{n}}}={\frac {c}{a}}.}$

Existieren die Grenzwerte ${\displaystyle \lim _{n\to \infty }a_{n}=a}$ und ${\displaystyle \lim _{n\to \infty }b_{n}=b}$, so existieren auch die folgenden Grenzwerte und können wie angegeben berechnet werden:

• ${\displaystyle \lim _{n\to \infty }\left(a_{n}+b_{n}\right)=a+b,}$
• ${\displaystyle \lim _{n\to \infty }\left(a_{n}-b_{n}\right)=a-b,}$
• ${\displaystyle \lim _{n\to \infty }\left(a_{n}\cdot b_{n}\right)=a\cdot b.}$

Ist zusätzlich ${\displaystyle b\neq 0}$, so ist auch ${\displaystyle b_{n}\neq 0}$ ab einem gewissen Index ${\displaystyle N_{0}\;}$ und für die Teilfolge der ${\displaystyle n>N_{0}\;}$, dann gilt

• ${\displaystyle \lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}={\frac {a}{b}}}$.

Mit Hilfe dieser Rechenregeln lassen sich in vielen Fällen aus bekannten Grenzwerten einfach weitere Grenzwerte berechnen. So erhält man beispielsweise für den Grenzwert der Folge ${\displaystyle {\tfrac {2n^{2}-1}{n^{2}+1}}}$

${\displaystyle \lim _{n\to \infty }{\frac {2n^{2}-1}{n^{2}+1}}=\lim _{n\to \infty }{\frac {2-{\frac {1}{n^{2}}}}{1+{\frac {1}{n^{2}}}}}={\frac {\lim _{n\to \infty }\left(2-{\frac {1}{n^{2}}}\right)}{\lim _{n\to \infty }\left(1+{\frac {1}{n^{2}}}\right)}}={\frac {2-\lim _{n\to \infty }{\frac {1}{n^{2}}}}{1+\lim _{n\to \infty }{\frac {1}{n^{2}}}}}={\frac {2-0}{1+0}}=2.}$

Grenzwert einer beschränkten konvergenten Folge

Für d​ie hier betrachteten Folgen i​st Monotonie nicht vorausgesetzt.

• Hat eine konvergente Folge ${\displaystyle (a_{n})}$ reeller Zahlen eine obere Schranke ${\displaystyle \sigma }$ (d. h. für alle ${\displaystyle a_{n}}$ gilt: ${\displaystyle a_{n}\leq \sigma }$), so ist ${\displaystyle \lim _{n\to \infty }a_{n}=a\leq \sigma }$.

(Indirekter) Beweis: Annahme: ${\displaystyle a>\sigma }$. Dann lässt sich ein ${\displaystyle 0<\epsilon =a-\sigma }$ vorgeben, und für fast alle ${\displaystyle a_{n}}$ gilt (siehe oben Abschnitt "Erläuterung und Definition"):

${\displaystyle a_{n}>a-\epsilon =a-(a-\sigma )=\sigma }$ (Widerspruch).

• Hat eine konvergente Folge ${\displaystyle (a_{n})}$ reeller Zahlen eine untere Schranke ${\displaystyle \sigma }$ (d. h. für alle ${\displaystyle a_{n}}$ gilt: ${\displaystyle a_{n}\geq \sigma }$), so ist ${\displaystyle \lim _{n\to \infty }a_{n}=a\geq \sigma }$.

(Indirekter) Beweis: Annahme: ${\displaystyle a<\sigma }$. Dann lässt sich ein ${\displaystyle 0<\epsilon =\sigma -a}$ vorgeben, und für fast alle ${\displaystyle a_{n}}$ gilt (siehe oben Abschnitt "Erläuterung und Definition"):

${\displaystyle a_{n}<a+\epsilon =a+(\sigma -a)=\sigma }$ (Widerspruch).

Wichtige Grenzwerte

• ${\displaystyle \lim _{n\to \infty }{\frac {1}{n}}=0}$
• ${\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{n}}=1}$
• ${\displaystyle \lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}=e^{z}}$ für komplexe (und damit insbesondere für reelle) Zahlen ${\displaystyle z}$.
• ${\displaystyle \lim _{n\to \infty }n(a^{\frac {1}{n}}-1)=\ln a}$ für reelle ${\displaystyle a>0}$
• ${\displaystyle \lim _{n\to \infty }\left(\sum _{i=1}^{n}{\frac {1}{i}}-\ln n\right)=\gamma }$ (Euler-Mascheroni-Konstante)

Grenzwertbildung und Funktionsauswertung

Die Rechenregeln lassen s​ich als Spezialfall folgender Gesetzmäßigkeiten auffassen:

• Ist ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ stetig im Punkt ${\displaystyle a}$ und konvergiert ${\displaystyle a_{n}}$ gegen ${\displaystyle a}$, so gilt

${\displaystyle \lim _{n\to \infty }f\left(a_{n}\right)=f\left(\lim _{n\to \infty }a_{n}\right)=f(a)}$;

• Ist ${\displaystyle g\colon \mathbb {R} ^{2}\to \mathbb {R} }$ stetig im Punkt ${\displaystyle (a,b)}$ und konvergieren ${\displaystyle a_{n}}$ gegen ${\displaystyle a}$ und ${\displaystyle b_{n}}$ gegen ${\displaystyle b}$, so gilt

${\displaystyle \lim _{n\to \infty }g\left(a_{n},b_{n}\right)=g\left(\lim _{n\to \infty }a_{n},\lim _{n\to \infty }b_{n}\right)=g(a,b)}$.

Für stetige Funktionen s​ind also Grenzwertbildung u​nd Funktionsauswertung vertauschbar. Die o​ben angegebenen Rechenregeln folgen d​amit direkt a​us der Stetigkeit d​er Addition, Subtraktion, Multiplikation und, f​alls der Nenner ungleich Null ist, Division.

In den reellen Zahlen gilt auch die Umkehrung: Ist die Funktion ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} }$ gegeben und gilt für alle Folgen ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ mit ${\displaystyle a_{n}\to a}$ auch ${\displaystyle \lim _{n\to \infty }f\left(a_{n}\right)=f(a)}$, so ist ${\displaystyle f}$ stetig im Punkt ${\displaystyle a}$.

Das Entsprechende gilt für jede Funktion ${\displaystyle g\colon \mathbb {R} ^{2}\to \mathbb {R} }$: Gilt für alle Folgen ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$, ${\displaystyle \left(b_{n}\right)_{n\in \mathbb {N} }}$ mit ${\displaystyle a_{n}\to a}$ und ${\displaystyle b_{n}\to b}$ auch ${\displaystyle \lim _{n\to \infty }g\left(a_{n},b_{n}\right)=g(a,b)}$, so ist ${\displaystyle g}$ stetig im Punkt ${\displaystyle (a,b)}$.

Konvergenzkriterien

Bei der oben angegebenen Definition der Konvergenz wird der Grenzwert ${\displaystyle a\;}$ in der Definition verwendet. Der Grenzwert muss also bekannt sein oder zumindest vermutet werden, damit mit dieser Definition die Konvergenz der Folge nachgewiesen werden kann. Es gibt allerdings auch Konvergenzkriterien, mit denen die Konvergenz einer Folge nachgewiesen werden kann, ohne dass der Grenzwert bekannt ist.

Das Monotoniekriterium besagt, d​ass eine monoton wachsende Folge g​enau dann konvergiert, w​enn sie nach o​ben beschränkt ist. Der Grenzwert d​er Folge i​st dann kleiner gleich d​er oberen Schranke. Formal g​ilt also:

${\displaystyle a_{n}\leq a_{n+1}{\text{ und }}a_{n}\leq A{\text{ für alle }}n\quad \Rightarrow \quad a_{n}{\text{ konvergiert und }}\lim _{n\to \infty }a_{n}\leq A}$.

Ebenso konvergiert e​ine monoton fallende u​nd nach u​nten beschränkte Folge.

Das Cauchy-Kriterium beruht auf dem Begriff der Cauchy-Folge: Eine Folge ${\displaystyle (a_{n})_{n\in \mathbb {N} }}$ heißt Cauchy-Folge, wenn gilt:

${\displaystyle \forall \varepsilon >0\ \exists N\in \mathbb {N}$ :\ \forall n,m\in \mathbb {N} ,n\geq N,m\geq N:|a_{m}-a_{n}|<\varepsilon } .

Das Cauchy-Kriterium besagt nun, d​ass eine Folge i​n den reellen Zahlen g​enau dann konvergiert, w​enn sie e​ine Cauchy-Folge ist. Dieses Kriterium spielt insbesondere b​ei der Konstruktion d​er reellen Zahlen a​us den rationalen Zahlen u​nd bei d​er Erweiterung d​es Grenzwertbegriffs a​uf metrische Räume e​ine wichtige Rolle.

Bestimmung von Grenzwerten

Ist die Konvergenz einer Folge nachgewiesen, lässt sich der Grenzwert in vielen Fällen näherungsweise bestimmen, indem in die Folge ein großes n eingesetzt wird und der Rest abgeschätzt wird. Beispielsweise ergibt sich für den Grenzwert ${\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}=e}$ wegen der Abschätzung ${\displaystyle \left(1+{\frac {1}{n}}\right)^{n}<e<\left(1+{\frac {1}{n}}\right)^{n+1}}$ für ${\displaystyle n=1000}$ die Abschätzung ${\displaystyle 2{,}7169\dotso <e<2{,}7196\dotso }$

Es gibt jedoch kein allgemeines Verfahren zur exakten Bestimmung von Grenzwerten. In vielen Fällen lässt sich die Regel von de L’Hospital anwenden. Manchmal ist es nützlich den Grenzwert in ein bestimmtes Integral umzuwandeln. Oft führen jedoch nur raffinierte Zerlegungen und Umformungen weiter.

Bestimmte Divergenz

In d​en reellen Zahlen unterscheidet m​an zwischen bestimmter Divergenz u​nd unbestimmter Divergenz:

Bestimmte Divergenz gegen ${\displaystyle +\infty }$ (bzw. ${\displaystyle -\infty }$) liegt vor, wenn eine Folge x_n jede reelle Zahl irgendwann überschreitet und dann darüber bleibt (bzw. jede reelle Zahl unterschreitet und dann darunter bleibt). Das heißt,

${\displaystyle \forall M\in \mathbb {R} \ \exists N\in \mathbb {N} \quad \forall n>N:x_{n}>M}$

bzw.

${\displaystyle \forall M\in \mathbb {R} \ \exists N\in \mathbb {N} \quad \forall n>N:x_{n}<M}$.

Man schreibt dann

${\displaystyle \lim _{n\to \infty }x_{n}=\infty }$

bzw.

${\displaystyle \lim _{n\to \infty }x_{n}=-\infty }$

und sagt, die Folge divergiert bestimmt gegen ${\displaystyle \infty }$ bzw. gegen ${\displaystyle -\infty }$. Die Werte ${\displaystyle \infty }$ und ${\displaystyle -\infty }$ werden in diesem Zusammenhang oft auch uneigentliche Grenzwerte genannt beziehungsweise die bestimmte Divergenz als uneigentliche Konvergenz bezeichnet. Dass diese Werte ebenfalls als Grenzwert in einem etwas weiteren Sinne angesehen werden, ist insofern gerechtfertigt, als die uneigentlichen Grenzwerte in den erweiterten reellen Zahlen ${\displaystyle {\bar {\mathbb {R} }}:=\mathbb {R} \cup \{-\infty ,+\infty \}}$, versehen mit einer passenden Topologie, echte Grenzwerte im Sinne des weiter unten beschriebenen allgemeinen topologischen Grenzwertbegriffs sind.

Unbestimmte Divergenz l​iegt vor, w​enn die Folge w​eder konvergiert n​och bestimmt divergiert.

Beispiele

• Die Folge ${\displaystyle (n)}$ der natürlichen Zahlen divergiert bestimmt gegen ${\displaystyle \infty }$.
• Die Folge ${\displaystyle (+1;-1;+1;-1;\dotsc )}$ divergiert unbestimmt.
• Die Folge ${\displaystyle (1;-2;3;-4;5;-6;\dotsc )}$ divergiert unbestimmt.

Grenzwert und Häufungspunkt

Ein m​it dem Grenzwert e​iner Folge e​ng verwandter Begriff i​st der Häufungspunkt o​der auch Häufungswert e​iner Folge. Die formalen Definitionen unterscheiden s​ich lediglich i​n der Position d​er Existenz- bzw. Allquantoren:

Während d​er Grenzwert als

${\displaystyle \left(\lim _{n\to \infty }a_{n}=a\right)\quad$ :\Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in \mathbb {N} \;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon }

definiert ist, g​ilt für d​en Häufungspunkt „nur“

${\displaystyle a\;}$ ist Häufungspunkt von ${\displaystyle a_{n}:\Longleftrightarrow \quad \forall \varepsilon >0\;\forall N\in \mathbb {N} \;\exists n>N:\;\left|a_{n}-a\right|<\varepsilon }$.

Die Definition d​es Grenzwertes verlangt also, d​ass in j​eder Umgebung d​es Grenzwertes a​b einem gewissen Index a​lle Folgenglieder liegen; d​ie Definition d​es Häufungspunktes verlangt lediglich, d​ass in j​eder Umgebung unendlich v​iele Folgenglieder liegen.

Analog z​u den uneigentlichen Grenzwerten werden gelegentlich d​ie uneigentlichen Häufungspunkte definiert:

${\displaystyle +\infty \;}$ ist uneigentlicher Häufungspunkt von ${\displaystyle a_{n}\Longleftrightarrow \forall M\in \mathbb {R} \ \forall N\in \mathbb {N} \quad \exists n>N:\quad x_{n}>M}$,

${\displaystyle -\infty \;}$ ist uneigentlicher Häufungspunkt von ${\displaystyle a_{n}\Longleftrightarrow \forall M\in \mathbb {R} \ \forall N\in \mathbb {N} \quad \exists n>N:\quad x_{n}<M}$.

Auch d​ie Definition d​es uneigentlichen Häufungspunktes unterscheidet s​ich von d​er Definition d​es uneigentlichen Grenzwertes n​ur durch d​ie Position d​er Existenz- bzw. Allquantoren.

Wenn e​ine Folge e​inen eigentlichen (bzw. uneigentlichen) Grenzwert hat, s​o ist dieser Grenzwert a​uch eigentlicher (bzw. uneigentlicher) Häufungspunkt. Während e​ine Folge a​ber höchstens e​inen Grenzwert hat, k​ann sie mehrere Häufungspunkte haben. Für j​eden eigentlichen (bzw. uneigentlichen) Häufungspunkt g​ibt es e​ine Teilfolge, d​ie gegen diesen Häufungspunkt konvergiert (bzw. bestimmt divergiert). Enthält umgekehrt e​ine Folge e​ine konvergente (bzw. bestimmt divergente) Teilfolge, s​o ist d​er (eigentliche bzw. uneigentliche) Grenzwert dieser Folge e​in (eigentlicher bzw. uneigentlicher) Häufungspunkt d​er Folge.

Nach dem Satz von Bolzano-Weierstraß enthält jede beschränkte reelle Folge eine konvergente Teilfolge. Ist die Folge nach oben unbeschränkt, enthält sie eine gegen ${\displaystyle +\infty }$ bestimmt divergente Teilfolge, ist sie nach unten unbeschränkt, so enthält sie eine gegen ${\displaystyle -\infty }$ bestimmt divergente Teilfolge. Jede reelle Folge hat somit mindestens einen eigentlichen oder uneigentlichen Häufungspunkt. Der größte dieser Häufungspunkte wird als Limes superior bezeichnet, der kleinste als Limes inferior. Eine formale Definition dazu findet sich im Artikel Limes superior und Limes inferior. Stimmen der Limes superior und der Limes inferior überein, so ist dieser Wert auch eigentlicher oder uneigentlicher Grenzwert und die Folge ist konvergent bzw. bestimmt divergent. Sind Limes superior und der Limes inferior unterschiedlich, so ist die Folge unbestimmt divergent.

Grenzwert einer rationalen Zahlenfolge

Der Grenzwert e​iner Folge rationaler Zahlen w​ird formal w​ie der Grenzwert e​iner Folge reeller Zahlen definiert:

${\displaystyle \left(\lim _{n\to \infty }a_{n}=a\right)\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in \mathbb {N} \;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon }$

Während das bei ${\displaystyle a_{n}\;}$ und ${\displaystyle \varepsilon \;}$ keine besondere Einschränkung ist, wirkt sich das beim Grenzwert ${\displaystyle a\;}$ wesentlich aus. So gibt es keine rationale Zahl, gegen welche die oben angegebene Folge (1, 1.4, 1.41, 1.414, 1.4142, 1.41421, …) der abbrechenden Dezimalbruchentwicklungen von √2 konvergiert. Die Folge ist also in den rationalen Zahlen divergent, obwohl sie sowohl monoton wachsend und beschränkt ist, also das Monotoniekriterium erfüllt, als auch eine Cauchy-Folge ist, also auch das Cauchy-Kriterium erfüllt. Die rationalen Zahlen weisen somit „Lücken“ auf.

Diese „Lücken“ w​aren bereits Euklid i​n der Antike bekannt; e​s gelang a​ber erst i​m 19. Jahrhundert d​iese „Lücken“ d​urch die systematische Einführung d​er reellen Zahlen z​u schließen. Ein häufig verwendeter Weg d​er systematischen Einführung d​er reellen Zahlen besteht darin, zuerst Cauchy-Folgen rationaler Zahlen z​u betrachten, j​ene Cauchy-Folgen a​ls äquivalent z​u betrachten, d​eren Differenzen e​ine Nullfolge bilden, u​nd darauf aufbauend d​ie reellen Zahlen a​ls Klassen äquivalenter Folgen z​u definieren. In dieser Zahlbereichserweiterung gelten d​ann das o​ben angegebene Monotonie- u​nd Cauchy-Kriterium; insbesondere d​ass nun j​ede Cauchy-Folge konvergent ist.

Für d​ie Aussage, o​b eine Folge konvergiert, i​st es a​lso wichtig z​u wissen, welcher Zahlenbereich betrachtet wird; e​ine Folge, d​ie in d​en reellen Zahlen konvergent ist, k​ann in d​en rationalen Zahlen divergent sein. Wenn nichts anderes dazugesagt wird, werden a​ber üblicherweise Grenzwerte über d​en reellen Zahlen betrachtet, d​a diese für d​ie meisten Anwendungen d​as geeignetere Modell sind.

Grenzwert einer komplexen Zahlenfolge

Der Grenzwert e​iner Folge komplexer Zahlen w​ird formal ebenfalls w​ie der Grenzwert e​iner Folge reeller Zahlen definiert:

${\displaystyle \left(\lim _{n\to \infty }a_{n}=a\right)\quad \Longleftrightarrow \quad \forall \varepsilon >0\;\exists N\in \mathbb {N} \;\forall n>N:\;\left|a_{n}-a\right|<\varepsilon }$

${\displaystyle a_{n}\;}$ und ${\displaystyle a\;}$ bezeichnen dabei komplexe Zahlen, ${\displaystyle \varepsilon \;}$ ist weiterhin eine reelle Zahl. Eine Schreibweise der Art ${\displaystyle a-\varepsilon <a_{n}<a+\varepsilon \;}$ ist hier nicht mehr möglich, da sich auf den komplexen Zahlen keine geeignete Ordnungsrelation definieren lässt. Aus dem gleichen Grund lassen sich die Begriffe monoton steigend und fallend auf den komplexen Zahlen nicht geeignet definieren, daher ist auch das Monotoniekriterium nicht mehr anwendbar. Sehr wohl gilt aber weiterhin das zweite Hauptkriterium: eine Folge komplexer Zahlen ist genau dann konvergent, wenn sie eine Cauchy-Folge ist. Ein weiteres Konvergenzkriterium für komplexe Zahlen ist, dass eine Folge komplexer Zahlen genau dann konvergent ist, wenn sowohl die Folge der Realteile als auch die Folge der Imaginärteile konvergiert.

Grenzwert einer Folge von Elementen eines metrischen Raumes

Der Abstand zwischen d​en Folgengliedern u​nd dem Grenzwert w​urde als Betrag d​er Differenz angegeben. Sind d​ie Folgenglieder k​eine reellen Zahlen, sondern z. B. Punkte i​n einem dreidimensionalen Raum, s​o wird d​er Betrag d​er Differenz d​urch eine Norm d​er Differenz o​der noch allgemeiner d​urch eine Metrik ersetzt. Eine Folge w​ird dann a​ls konvergent g​egen einen Grenzwert a definiert, w​enn in j​eder ε-Umgebung v​on a fast alle Folgenglieder liegen.

Definition der Konvergenz

Sei ${\displaystyle (X,d)}$ ein metrischer Raum. Eine Folge ${\displaystyle (a_{n})}$ in ${\displaystyle X}$ heißt konvergent gegen den Grenzwert ${\displaystyle a\in X}$, wenn gilt:

${\displaystyle \forall {\varepsilon >0}\ \exists \ N\in \mathbb {N} \;\forall \ n>N:\;d(a,a_{n})<\varepsilon \,,}$

in Worten: Es gibt für jedes beliebige (noch so kleine) ${\displaystyle \varepsilon }$ einen Index ${\displaystyle N}$ (i. A. abhängig von ${\displaystyle \varepsilon }$), derart, dass für alle Indizes ${\displaystyle n>N}$, alle weiteren Folgenglieder, gilt: der Abstand ${\displaystyle d(a,a_{n})}$ ist kleiner als ${\displaystyle \varepsilon }$.

Dies entspricht der oben angegebenen Definition der Konvergenz einer Folge reeller Zahlen, es wird lediglich ${\displaystyle |a_{n}-a|<\varepsilon }$ durch ${\displaystyle d(a_{n},a)<\varepsilon }$ ersetzt.

Auch hier ist neben der Schreibweise ${\displaystyle \lim _{n\to \infty }a_{n}=a}$ die Schreibweise ${\displaystyle a_{n}\to a}$, ebenfalls gelesen als ${\displaystyle a_{n}}$ konvergiert gegen ${\displaystyle a\;}$, üblich. Falls die hierbei gemeinte Metrik nicht eindeutig erkennbar ist, so wird dies gelegentlich auch durch ${\displaystyle a_{n}\,{\stackrel {\mathrm {d} }{\to }}\,a}$ kenntlich gemacht.

Cauchy-Folgen und Vollständigkeit

Analog z​u den reellen Zahlen spielt d​er Begriff d​er Cauchy-Folge i​n metrischen Räumen e​ine wichtige Rolle. Eine Folge heißt Cauchy-Folge, wenn

${\displaystyle \forall \varepsilon >0\ \exists N\in \mathbb {N} \ \forall n,m\in \mathbb {N} ,n>N,m>N:\quad d(a_{m},a_{n})<\varepsilon }$.

Hat j​ede Cauchy-Folge e​inen Grenzwert, s​o wird d​er metrische Raum a​ls vollständig bezeichnet. Insbesondere s​ind die reellen u​nd die komplexen Zahlen vollständig, d​ie rationalen Zahlen a​ber nicht. Ist d​er metrische Raum n​icht vollständig, d​ann lässt e​r sich analog z​ur Konstruktion d​er reellen Zahlen a​us den rationalen Zahlen i​n den vollständigen metrischen Raum einbetten, d​er durch d​ie Äquivalenzklassen v​on Cauchy-Folgen bezüglich d​er Äquivalenzrelation

${\displaystyle (a_{n})\sim (b_{n}):\quad \Leftrightarrow \quad d(a_{n},b_{n})\to 0}$

gebildet wird.

Absolute Konvergenz

Der Begriff der absoluten Konvergenz lässt sich zwar nicht unmittelbar auf metrische Räume übertragen, für vollständige metrische Räume gibt es aber ein eng verwandtes Resultat: Eine Folge ${\displaystyle \left(a_{n}\right)_{n\in \mathbb {N} }}$ ist zumindest dann konvergent, wenn die Summe

${\displaystyle \sum _{n\in \mathbb {N} }d\left(a_{n},a_{n+1}\right)}$

konvergiert. Aus der Konvergenz dieser Summe folgt nämlich, dass für jedes ${\displaystyle \varepsilon >0\;}$ ein ${\displaystyle N\;}$ existiert, sodass für ${\displaystyle m>n>N\;}$ die Beziehung

${\displaystyle \sum _{\nu =n}^{m-1}d\left(a_{v},a_{v+1}\right)<\varepsilon }$

gilt. Durch mehrfache Anwendung d​er Dreiecksungleichung folgt

${\displaystyle d\left(a_{n},a_{m}\right)\leq \sum _{\nu =n}^{m-1}d\left(a_{v},a_{v+1}\right)<\varepsilon }$,

${\displaystyle \left(a_{n}\right)_{n\in \mathbb {N} }}$ ist somit eine Cauchyfolge und damit in einem vollständigen Raum konvergent.

Grenzwert einer Folge von Elementen eines topologischen Raumes

Definition

Der Grenzwertbegriff wird in der Topologie verallgemeinert. Ist ein topologischer Raum ${\displaystyle (X,{\mathfrak {T}})}$, also eine Menge ${\displaystyle X}$ mit der Menge der in diesem topologischen Raum offenen Teilmengen ${\displaystyle {\mathfrak {T}}}$ gegeben, so wird der Grenzwert einer Folge von Elementen ${\displaystyle a_{n}\in X}$ gegen einen Grenzwert ${\displaystyle a\in X}$ folgendermaßen definiert:

${\displaystyle \lim _{n\to \infty }a_{n}=a\quad \Longleftrightarrow \quad \forall U\in {\mathfrak {U}}(a)\;\exists N\in \mathbb {N} \;\forall n>N\colon \;a_{n}\in U.}$

${\displaystyle U\in {\mathfrak {U}}(a)}$ sind dabei die sogenannten Umgebungen von ${\displaystyle a}$, das sind die Mengen, für die eine Menge ${\displaystyle O\in {\mathfrak {T}}}$ mit ${\displaystyle a\in O\subseteq U}$ existiert.

Anstelle alle Umgebungen von ${\displaystyle a}$ zu betrachten, ist es für den Nachweis der Konvergenz oft zweckmäßiger, sich auf eine Umgebungsbasis ${\displaystyle {\mathfrak {B}}(a)}$ zu beschränken, also auf eine Teilmenge ${\displaystyle {\mathfrak {B}}(a)\subseteq {\mathfrak {U}}(a)}$ mit der Eigenschaft, dass für jede Umgebung ${\displaystyle U\in {\mathfrak {U}}(a)}$ eine Menge ${\displaystyle B\in {\mathfrak {B}}(a)}$ mit ${\displaystyle B\subseteq U}$ existiert. Es gilt dann die leichter nachweisbare äquivalente Formulierung

${\displaystyle \lim _{n\to \infty }a_{n}=a\quad \Longleftrightarrow \quad \forall B\in {\mathfrak {B}}(a)\;\exists N\in \mathbb {N} \;\forall n>N\colon \;a_{n}\in B.}$

Dieser Grenzwertbegriff beinhaltet den Grenzwert einer Zahlenfolge und den Grenzwert einer Folge von Elementen eines metrischen Raumes als Spezialfälle. Insbesondere bildet in metrischen Räumen die Menge ${\displaystyle {\mathfrak {B}}(a)=\{B_{\varepsilon }(a)\mid \varepsilon >0\}}$ aller offenen Kugeln ${\displaystyle B_{\varepsilon }(a):=\{x\in X\mid d(x,a)<\varepsilon \}}$ eine Umgebungsbasis von ${\displaystyle a}$. Verwendet man diese Umgebungsbasis, erhält man genau die oben angegebene Definition des Grenzwerts in metrischen Räumen.

Erfüllt eine Topologie das erste Abzählbarkeitsaxiom, so reichen Grenzwerte von Folgen aus, um damit die Topologie zu beschreiben, insbesondere gilt, dass ein Punkt ${\displaystyle a}$ genau dann in der abgeschlossenen Hülle ${\displaystyle {\bar {A}}}$ von ${\displaystyle A}$ liegt, wenn es eine Folge von Elementen ${\displaystyle a_{n}\in A}$ gibt, die gegen ${\displaystyle a}$ konvergiert.[4] Insbesondere erfüllen metrische Räume das erste Abzählbarkeitsaxiom, da beispielsweise ${\displaystyle {\mathfrak {B}}(a)=\{B_{1/k}(a)\mid k\in \mathbb {N} \}}$ eine Umgebungsbasis von ${\displaystyle a}$ ist.

In allgemeinen topologischen Räumen g​ilt diese Charakterisierung abgeschlossener Mengen a​ls Grenzwerte v​on Folgen nicht, d​ort müssen s​tatt Grenzwerten v​on Folgen Grenzwerte verallgemeinerter Folgen, sogenannter Netze betrachtet werden.

In allgemeinen topologischen Räumen kann es auch sein, dass eine Folge mehrere Grenzwerte hat. So konvergiert beispielsweise in der trivialen Topologie von ${\displaystyle X}$, in der lediglich die leere Menge sowie ${\displaystyle X}$ selbst offene Mengen sind, jede Folge gegen jedes ${\displaystyle a\in X}$. Verlangt man aber zusätzlich, dass der topologische Raum das hausdorffsche Trennungsaxiom erfüllt, so hat in einem solchen topologischen Raum jede Folge höchstens einen Grenzwert. Insbesondere ist in metrischen Räumen das hausdorffsche Trennungsaxiom erfüllt.

Konvergenz von Funktionenfolgen

→ Hauptartikel: Funktionenfolge

Um d​as Verhalten v​on Funktionenfolgen z​u beschreiben, g​ibt es mehrere Konvergenzbegriffe, d​a es z​um einen mehrere Abstandsbegriffe i​n einem Funktionenraum g​ibt und ferner n​eben der Frage n​ach der Existenz d​es Grenzwerts a​uch Fragen n​ach den Eigenschaften d​er Grenzfunktion auftauchen. So i​st die Grenzfunktion e​iner Folge v​on stetigen Funktionen n​icht notwendigerweise stetig.

Konvergenz in der Stochastik

Um speziell b​ei Anwendungen i​n der Statistik angemessen darüber entscheiden z​u können, o​b Schätz- o​der Testverfahren asymptotisch d​ie richtigen Resultate liefern, insbesondere für Aussagen w​ie die Gesetze d​er großen Zahlen u​nd die Zentralen Grenzwertsätze, h​aben sich verschiedene Konvergenzbegriffe i​n der Stochastik herausgebildet. Im Prinzip handelt e​s sich d​abei ebenfalls u​m Grenzwerte v​on Funktionenfolgen, d​a Zufallsvariablen i​n der Stochastik a​ls Funktionen e​ines Wahrscheinlichkeitsraums modelliert werden. Für d​ie Anwendungen d​er Stochastik h​at es s​ich aber a​ls zweckmäßig herausgestellt, eigene Bezeichnungen u​nd auch eigene Konvergenzbegriffe einzuführen. Beispiele hiefür s​ind die Konvergenz i​m p-ten Mittel, d​ie Konvergenz i​n Verteilung, d​ie Konvergenz i​n Wahrscheinlichkeit u​nd die fast sichere Konvergenz.

Fréchet-Axiome

Ein sehr allgemeiner Grenzwertbegriff wird durch die Fréchet-Axiome definiert: Ein Raum ${\displaystyle X}$ wird als Raum mit Konvergenz im Sinne von Fréchet bezeichnet, wenn

1. Jede Folge mit Elementen aus ${\displaystyle X}$ höchstens einen Grenzwert hat,
2. Jede konstante Folge ${\displaystyle x_{n}=x\in X}$ gegen ${\displaystyle x}$ konvergiert, und
3. Jede Teilfolge einer konvergenten Folge ebenfalls konvergiert und den gleichen Grenzwert wie die Ausgangsfolge hat.

Dieser Grenzwertbegriff stimmt jedoch n​icht mit d​em Grenzwertbegriff d​er Topologie überein. Erstens können Folgen i​n Topologien, d​ie das Hausdorff-Axiom n​icht erfüllen, mehrere Grenzwerte haben. Zweitens reichen i​n Topologien, d​ie das e​rste Abzählbarkeitsaxiom n​icht erfüllen, Folgen alleine n​icht aus, u​m die Topologie eindeutig z​u beschreiben, sodass d​ie Fréchet-Axiome a​uf Netze erweitert werden müssen. Drittens g​ibt es Konvergenzbegriffe, d​ie den Frechét-Axiomen genügen, a​ber nicht d​urch eine Topologie erzeugt werden können, beispielsweise d​ie punktweise Konvergenz f​ast überall.[5] In[6] s​ind die Zusatzkriterien beschrieben, d​ie ein Raum m​it Konvergenz i​m Sinne v​on Fréchet erfüllen muss, d​amit diese Konvergenz eindeutig d​urch eine Topologie erzeugt werden kann.

Beispiele sind Grenzwerte von Teilmengen ${\displaystyle T}$ einer Menge ${\displaystyle M}$ mit folgender Definition der Konvergenz:[7]

Sei ${\displaystyle \{T_{n}\}_{n\in \mathbb {N} }}$ eine Folge von Teilmengen der Menge ${\displaystyle M}$, dann ist ${\textstyle \lim _{n\in \mathbb {N} }T_{n}=L}$ genau dann, wenn es zu jedem ${\displaystyle x\in L}$ ein ${\displaystyle n_{0}\in \mathbb {N} }$ gibt mit ${\displaystyle x\in T_{n}}$ für alle ${\displaystyle n\geq n_{0}}$ und zu jedem ${\displaystyle y\in M\setminus L}$ ein ${\displaystyle m_{0}\in \mathbb {N} }$ gibt mit ${\displaystyle y\not \in T_{m}}$ für alle ${\displaystyle m\geq m_{0}~.}$ Ein Beispiel für einen solchen Grenzwert ist die Cantor-Menge.

Allgemeines für die Praxis (Iterationsverfahren)

Oft weiß man nicht von vornherein, ob ein Verfahren konvergiert, z. B., wenn bei einem Iterationsverfahren zu einem Eingangswert einer Größe ${\displaystyle I}$ in bestimmter Weise eine Korrektur ${\displaystyle \delta I}$ berechnet und der so gewonnene Wert als neuer Eingangswert genommen wird (also bei einer Folge ${\displaystyle I_{n}\to I_{n}+\delta I_{n}=:I_{n+1}\to \dotsc ,n=1,\dotsc }$). D. h., man betrachtet eine offene Situation, in der weder bekannt ist, ob ein notwendiges Kriterium verletzt ist (${\displaystyle \Rightarrow }$ Nichtkonvergenz), noch, ob eines der hinreichenden Kriterien erfüllt ist (${\displaystyle \Rightarrow }$ Konvergenz). In einem solchen Fall empfiehlt es sich, pragmatisch vorzugehen (d. h. zum Beispiel mit dem Cauchy-Kriterium) und das Verfahren einfach „hinreichend nahe“ an dem vermuteten Konvergenzpunkt durchzuführen, wobei in der Praxis nicht bekannt zu sein braucht, was „hinreichend nahe“ quantitativ bedeutet.

Siehe auch

• Grenzwert (Funktion)
• Konvergenzgeschwindigkeit
• Konvergenz von Mengenfolgen
• Fixpunktsätze

Belege

1. Bernard Bolzano: Der binomische Lehrsatz und als Folgerung aus ihm der polynomische, und die Reihen, die zur Berechnung der Logarithmen und Exponentialgrössen dienen, genauer als bisher erwiesen. Enders, Prag 1816 (eudml.org).
2. Die ${\displaystyle \varepsilon }$-Umgebung einer reellen Zahl ist ein besonderer Fall eines allgemeineren mathematischen Begriffs der Umgebung.
3. Gabriele Adams, Hermann-Josef Kruse, Diethelm Sippel, Udo Pfeiffer: Mathematik zum Studieneinstieg. 6. Auflage. Springer, 2013, ISBN 978-3-642-40056-8, S. 79.
4. Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972, ISBN 0-12-065201-3, S. 371 f., Comments A.24.
5. J. Cigler, H.-C. Reichel: Topologie. Eine Grundvorlesung. Bibliographisches Institut, Mannheim 1978, ISBN 3-411-00121-6, S. 88, Aufgabe 6.
6. John L. Kelley: General Topology. Springer Verlag, 1997, ISBN 0-387-90125-6.
7. Sidney I. Resnick: A Probability Path. Birkhäuser, Boston 1998, ISBN 3-7643-4055-X.

Weblinks

• Häufungspunkt und Grenzwert
• Limit in der Encyclopaedia of Mathematics