Satz vom Minimum und Maximum

Der Satz v​om Minimum u​nd Maximum i​st ein mathematischer Lehrsatz a​us dem Gebiet d​er Analysis, d​er dem deutschen Mathematiker Karl Weierstraß zugerechnet wird. Der Satz besagt, d​ass jede a​uf einem kompakten reellen Intervall definierte, reellwertige u​nd stetige Funktion beschränkt i​st und i​m Definitionsbereich ihr Maximum s​owie Minimum annimmt. Er i​st einer d​er Hauptsätze d​er Analysis u​nd stellt e​in wichtiges Instrument z​um Beweis d​er Existenz v​on Extremwerten solcher Funktionen dar.

Eine auf [a,b] definierte stetige Funktion, die ihr Maximum und Minimum annimmt

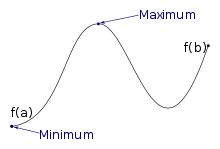
Satz vom Minimum und Maximum

Der Satz lässt s​ich in mehreren Fassungen formulieren:

(Ia) Jede auf einem kompakten Intervall ${\displaystyle [a,b]\subset \mathbb {R} \;(a\leq b)}$ definierte stetige Funktion ist dort beschränkt und nimmt dort ein Maximum und ein Minimum an.

Oder ausführlich:

(Ib) Ist ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ eine stetige Funktion, so gibt es stets Argumente ${\displaystyle {\tilde {x}},{\hat {x}}\in [a,b]}$ derart, dass für jedes andere Argument ${\displaystyle x\in [a,b]}$ die Ungleichung ${\displaystyle f({\hat {x}})\leq f(x)\leq f({\tilde {x}})}$ erfüllt ist.

Oder k​urz und u​nter Einbeziehung d​es Zwischenwertsatzes:

(II) Für jede stetige Funktion ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ existieren Argumente ${\displaystyle {\tilde {x}},{\hat {x}}\in [a,b]}$ mit ${\displaystyle f([a,b])=[f({\hat {x}}),f({\tilde {x}})]}$ .

Beweis

Voraussetzung: Sei ${\displaystyle f\colon [a,b]\to \mathbb {R} }$ eine stetige Funktion mit ${\displaystyle a,b\in \mathbb {R} }$ und ${\displaystyle a\leq b}$.

${\displaystyle M=f([a,b])}$ sei die Menge aller Funktionswerte, die ${\displaystyle f}$ annimmt.

Die Folgen ${\displaystyle (y_{n}),y_{n}\in M}$ und ${\displaystyle (x_{n}),x_{n}\in [a,b]}$ mit jeweils ${\displaystyle n\in \mathbb {N} }$ heißen zugehörig, wenn für je ein Folgenglied gilt: ${\displaystyle f(x_{n})=y_{n}}$.

${\displaystyle (x_{k})}$ bzw. ${\displaystyle (y_{k})}$ sei eine durch geeignete Auswahl aus ${\displaystyle (x_{n})}$ bzw. ${\displaystyle (y_{n})}$ entstehende Teilfolge, wobei ${\displaystyle k\in K\subset \mathbb {N} }$.

A. Behauptung: Jede Folge ${\displaystyle (y_{n})}$ hat eine Teilfolge ${\displaystyle (y_{k})}$, die gegen ein ${\displaystyle y_{l}\in M}$ konvergiert.

Beweis: Die ${\displaystyle (y_{n})}$ zugehörige Folge ${\displaystyle (x_{n})}$ ist wegen ${\displaystyle x_{n}\in [a,b]}$ beschränkt. Mit dem Satz von Bolzano-Weierstraß lässt sich aus ${\displaystyle (x_{n})}$ eine konvergente Teilfolge ${\displaystyle (x_{k})}$ auswählen. Da ${\displaystyle [a,b]}$ kompakt ist, konvergiert ${\displaystyle (x_{k})}$ gegen ein ${\displaystyle x_{l}\in [a,b]}$. Da ${\displaystyle f}$ in ${\displaystyle [a,b]}$ stetig ist, konvergiert die zugehörige Folge ${\displaystyle (y_{k})}$ nach dem Folgenkriterium der Stetigkeit gegen ${\displaystyle y_{l}=f(x_{l})\in M}$.

B. Behauptung: ${\displaystyle f}$ ist in [a,b] nach oben beschränkt.

Der Beweis wird indirekt geführt. - Annahme: ${\displaystyle f}$ ist nicht nach oben beschränkt.

Dann gibt es eine streng monoton steigende und (bestimmt) divergente Folge ${\displaystyle (y_{n})}$.[1] Jede Teilfolge ${\displaystyle (y_{k})}$ von ${\displaystyle (y_{n})}$ ist ebenfalls divergent. Das ist widersprüchlich, denn mit A. lässt sich aus ${\displaystyle (y_{n})}$ eine konvergente Teilfolge ${\displaystyle (y_{k})}$ auswählen.

Also ist ${\displaystyle f}$ nach oben beschränkt, und ${\displaystyle M}$ hat ein Supremum ${\displaystyle s\in \mathbb {R} }$.

C. Behauptung: ${\displaystyle f}$ nimmt in [a,b] ein Maximum an.

Aus geeignet gewählten Elementen von ${\displaystyle M}$ lässt sich eine Folge ${\displaystyle (y_{n})}$ erstellen, die gegen das Supremum ${\displaystyle s}$ von ${\displaystyle M}$ konvergiert.[2] Jede Teilfolge ${\displaystyle (y_{k})}$ von ${\displaystyle (y_{n})}$ konvergiert ebenfalls gegen ${\displaystyle s}$. Mit A. gibt es eine Teilfolge ${\displaystyle (y_{k})}$ von ${\displaystyle (y_{n})}$, die gegen ${\displaystyle y_{l}=f(x_{l})\in M}$ konvergiert. Wegen der Eindeutigkeit des Grenzwerts ist ${\displaystyle s=y_{l}}$ das Maximum der Behauptung.

D. Behauptung: ${\displaystyle f}$ ist in [a,b] nach unten beschränkt und nimmt dort ein Minimum an.

Zum Beweis i​st in B. u​nd C. "oben" d​urch "unten", "steigend" d​urch "fallend", "Supremum" d​urch "Infimum" u​nd "Maximum" d​urch "Minimum" z​u ersetzen.[3]

Bemerkungen

• Der Satz ist ein reiner Existenzsatz. Er ist nicht konstruktiv. Das heißt: Er liefert kein Verfahren, die Extremalstellen tatsächlich zu bestimmen. Bei differenzierbaren Funktionen können die Methoden der Kurvendiskussion genutzt werden, um die Extrema einer Funktion zu bestimmen.
• Der Satz vom Minimum und Maximum ist in bestimmtem Sinne charakteristisch für ${\displaystyle \mathbb {R} }$. Seine uneingeschränkte Gültigkeit ist gleichwertig mit dem Supremumsaxiom.

Verallgemeinerung

Der gleiche Satz - gemäß d​en Fassungen (Ia) o​der (Ib) - g​ilt auch noch, w​enn anstelle e​ines kompakten reellen Intervalls e​in beliebiger kompakter topologischer Raum zugrundegelegt wird: Stetige Bilder v​on kompakten topologischen Räumen u​nter reellwertigen Funktionen s​ind innerhalb d​er reellen Zahlen s​tets abgeschlossen u​nd beschränkt.[4][5][6]

Tatsächlich kann diese Aussage noch weiter verallgemeinert werden: Das Bild eines kompakten topologischen Raums unter einer stetigen Funktion ist wieder kompakt. Da kompakte Teilmengen von metrischen Räumen (insbesondere also von ${\displaystyle \mathbb {R} }$) immer abgeschlossen und beschränkt sind, folgt sofort die obige Aussage.

Da auch die Bilder zusammenhängender topologischer Räume unter stetigen Funktionen wieder zusammenhängend sind und die zusammenhängenden Teilmengen von ${\displaystyle \mathbb {R} }$ gerade die Intervalle sind, stellt sich auch die Fassung (II) als Spezialfall eines allgemeinen topologischen Sachverhalts dar.

Quellen und Hintergrundliteratur

• Otto Forster: Analysis 2 (= Grundkurs Mathematik). 8., aktualisierte Auflage. Vieweg+Teubner, Wiesbaden 2008, ISBN 978-3-8348-9541-7.
• Horst Schubert: Topologie. Eine Einführung (= Mathematische Leitfäden). 4. Auflage. B. G. Teubner Verlag, Stuttgart 1975, ISBN 3-519-12200-6. MR0423277

Einzelnachweise

1. Ein Beispiel ist die rekursiv definierte Folge ${\displaystyle (y_{n})}$: ${\displaystyle y_{0}}$ beliebig, ${\displaystyle y_{n}+1\leq y_{n+1}}$ beliebig.
2. Ein Beispiel ist die rekursiv definierte Folge ${\displaystyle (y_{n})}$: ${\displaystyle y_{0}}$ beliebig, ${\displaystyle s\geq y_{n+1}\geq (s+y_{n})/2}$.
3. Im Beweis der Existenz des Minimums sind Beispiele für rekursiv definierte Folgen des Beweisgangs: in B. ${\displaystyle (y_{n})}$: ${\displaystyle y_{0}}$ beliebig, ${\displaystyle y_{n}-1\geq y'_{n+1}}$ beliebig, bzw. in C. ${\displaystyle (y_{n})}$: ${\displaystyle y_{0}}$ beliebig, ${\displaystyle s\leq y_{n+1}\leq (s+y_{n})/2}$ beliebig.
4. Horst Schubert: Topologie. 1975, S. 62
5. Der Satz vom Minimum und Maximum lässt sich sogar auf den Fall der halbstetigen Funktionen ausdehnen. Siehe Beweisarchiv.
6. Es gibt eine weitere Verallgemeinerung, der auch den Fall der folgenkompakten Räume einbezieht.