Manhattan-Metrik

Die Manhattan-Metrik (auch Manhattan-Distanz, Mannheimer Metrik, Taxi- oder Cityblock-Metrik) ist eine Metrik, in der die Distanz $d$ zwischen zwei Punkten $A$ und $B$ als die Summe der absoluten Differenzen ihrer Einzelkoordinaten definiert wird:[1]

d(A,B)=\sum _{i}\left|A_{i}-B_{i}\right|

Die Linien in rot, blau und gelb sind drei Beispiele für die Manhattan-Distanz zwischen den zwei schwarzen Punkten (je 12 Einheiten lang); die grüne Linie stellt zum Vergleich den Euklidischen Abstand dar, der eine Länge von

6{\sqrt {2}}\approx 8.5

Einheiten hat.

Die zugrundeliegende Geometrie wurde zuerst von Hermann Minkowski untersucht.

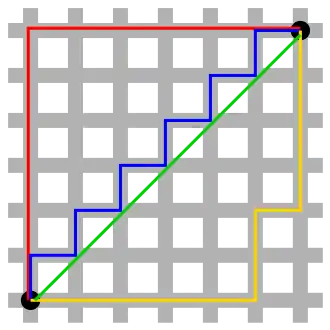
Ihren Namen hat diese Distanzdefinition von der Schachbrettmuster-artigen Anlage der Gebäudeblöcke und dem orthogonalen Straßengitter Manhattans, die einen Taxifahrer zwingen, die Entfernung zwischen zwei Adressen durch Aneinanderreihung „vertikaler“ und „horizontaler“ Wegstücke zu überwinden. Die Innenstadt Mannheims weist eine vergleichbare Struktur auf.

Ein Taxifahrer, der seine Route durch ein derartiges System plant, legt auf der Fahrt zu seinem Ziel immer die gleiche Streckenlänge zurück, sofern er nur Wege benutzt, die ihn seinem Ziel näher bringen. Dabei verlässt er niemals ein am Raster ausgerichtetes Rechteck, dessen gegenüberliegende Ecken auf dem Start- und dem Zielpunkt liegen.

Die Manhattan-Metrik ist die von der Summennorm (1-Norm) eines Vektorraums erzeugte Metrik.

So ist beispielsweise in der nebenstehenden Grafik die Manhattan-Metrik in einem zweidimensionalen Raum, sodass sich

d(A,B)=|A_{1}-B_{1}|+|A_{2}-B_{2}|=|6|+|6|=12

ergibt, wobei $A=(A_{1},A_{2})$ und $B=(B_{1},B_{2})$ die schwarz markierten Punkte sind.

Siehe auch

Französische Eisenbahnmetrik

Weblinks

Eric W. Weisstein: Taxicab Metric. In: MathWorld (englisch).

Einzelnachweise

Christian Royer: Simultane Optimierung von Produktionsstandorten, Produktionsmengen und Distributionsgebieten. Utz, Wiss., München 2001, ISBN 3-8316-0042-2, S. 55.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Christian Royer: Simultane Optimierung von Produktionsstandorten, Produktionsmengen und Distributionsgebieten. Utz, Wiss., München 2001, ISBN 3-8316-0042-2, S. 55.