Symmetrie (Geometrie)

Mit dem geometrischen Begriff Symmetrie (altgriechisch συμμετρία symmetria Ebenmaß, Gleichmaß, aus σύν syn „zusammen“ und μέτρον metron, Maß) bezeichnet man die Eigenschaft, dass ein geometrisches Objekt durch Bewegungen auf sich selbst abgebildet werden kann, also unverändert erscheint. Eine Umwandlung, die ein Objekt auf sich selbst abbildet, heißt Symmetrieabbildung oder Symmetrieoperation.

Symmetrie und Asymmetrie

Symmetrie

in der Architektur

in der Biologie

Leonardo da Vincis „vitruvianischer Mensch“

Manchmal werden auch zwei (oder mehr) verschiedene geometrische Objekte als zueinander symmetrisch bezeichnet, wenn sie, zusammen betrachtet, eine symmetrische Figur bilden.

Abhängig von der Zahl der betrachteten Dimensionen gibt es folgende unterschiedliche Symmetrien:

Symmetrien im Eindimensionalen

Im Eindimensionalen, also auf einer Geraden, gibt es die Symmetrie zu einem einzelnen Punkt sowie die Symmetrie der Translation (Verschiebung).

Symmetrien im Zweidimensionalen

Im Zweidimensionalen muss zwischen Punkt- und Achsensymmetrie unterschieden werden. Daneben treten auch hier Translationssymmetrien auf, aber auch andere Symmetrieformen, die es im Eindimensionalen nicht geben kann.

Rotationssymmetrie / Drehsymmetrie

Vier reguläre Polygone und zwei weitere geometrische Figuren mit den Kennzahlen ihrer Rotationssymmetrie, auch Drehsymmetrie genannt (n=1 bedeutet: ohne Drehsymmetrie)

Eine zweidimensionale geometrische Figur besitzt dann die Eigenschaft, rotationssymmetrisch zu sein, wenn die Figur einen zentralen Punkt besitzt, und die Figur auf sich selbst abgebildet wird, wenn man sie um diesen Punkt dreht. Ein Kreis oder ein Kreisring sind rotationssymmetrisch im engeren Sinne. Eine Drehung um jeden beliebigen Winkel bildet sie auf sich selbst ab.

Rotationssymmetrisch wird eine Figur auch dann genannt, wenn sie auf sich abgebildet werden kann, indem sie um einen festen Winkel $\varphi$ mit 0°< $\varphi$ < 360° um den zentralen Punkt gedreht wird.[1] Der Drehwinkel kann nur durch Division des vollen Winkels durch eine natürliche Zahl $n$ >1 entstehen, also $\varphi ={\tfrac {360^{\circ }}{n}}$ . Diese Zahl $n$ ist eine Kennzahl der Rotationssymmetrie und wird auch „Zähligkeit“ genannt.[2] Entsprechend heißt diese Symmetrie auch $n$ -zählige oder $n$ -fache Rotationssymmetrie (analog zum Englischen „ $n$ -fold rotational symmetry“) oder auch " $n$ -zählige Drehsymmetrie".[3]

Reguläre Polygone sind typische drehsymmetrische Figuren. Die rechts stehende Grafik zeigt die ersten vier, wobei die jeweils größtmögliche Kennzahl $n$ der Rotationssymmetrie mit eingezeichnet worden ist. Außerdem sind zwei weitere Figuren dargestellt, und zwar eine ohne und eine mit 2-facher Rotationssymmetrie. Im Trivialfall $n=1$ liegt keine Rotationssymmetrie/Drehsymmetrie vor und die Kennzahl 1 wird im mathematischen Kontext nicht verwendet, es sei denn, man möchte die triviale zyklische Gruppe $C_{1}$ kennzeichnen, die nur aus der identischen Abbildung besteht.

Die Schoenflies-Symbolik legt für die Symmetrieelemente und Symmetriegruppen der Rotationssymmetrie das Symbol $C_{n}$ fest. Weitere Beispiele für 2-fache Rotationssymmetrie sind die weiter unten abgebildeten punktsymmetrischen Figuren. Dass punktsymmetrische Objekte stets auch rotationssymmetrisch sind, gilt jedoch nur im Zweidimensionalen.

Spiegelsymmetrie / Achsensymmetrie

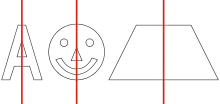
Spiegelsymmetrische Objekte in der Ebene

Alle Symmetrieelemente der obigen Polygone, einschließlich ihrer Spiegelsymmetriegeraden

Die Spiegelsymmetrie ist eine Form der Symmetrie, die bei Objekten auftritt, die senkrecht zu einer Symmetrieachse gespiegelt sind (siehe Zeichnung rechts).[4] Im Zweidimensionalen ist sie gleichbedeutend mit axialer Symmetrie oder Achsensymmetrie. Für jede Achsenspiegelung gilt:

Figur und Bildfigur sind deckungsgleich zueinander.
Strecke und Bildstrecke sind gleich lang.
Winkel und Bildwinkel sind gleich groß.
Figur und Bildfigur haben verschiedenen Umlaufsinn, sofern in der Figur ein Umlaufssinn definiert ist.

Beispiele

Dreiecke können eine oder drei Spiegelsymmetrieachsen haben: Ein gleichschenkliges Dreieck ist achsensymmetrisch zur Mittelsenkrechten der Basis. Homogene gleichseitige Dreiecke haben drei Spiegelsymmetrieachsen, wie die nebenstehende Grafik zeigt. Die Tatsache, dass bei diesen farbig dargestellten Polygonen die Zahl der Symmetrieachsen mit der oben genannten Zähligkeit für die Drehsymmetrie jeweils übereinstimmt, gilt nicht allgemein, denn es gibt viele drehsymmetrische Objekte, die keine Spiegelsymmetrie aufweisen, beispielsweise die weiter unten abgebildeten punktsymmetrischen Formen.
Vierecke können eine, zwei oder sogar vier Spiegelsymmetrieachsen besitzen:
- Mindestens eine Spiegelsymmetrieachse haben gleichschenklige Trapeze (durch die Mittelpunkte der parallelen Seiten) und Drachenvierecke (entlang einer Diagonale).
- Mindestens zwei Spiegelsymmetrieachsen liegen vor beim Rechteck (die Mittelsenkrechten von gegenüber liegenden Seiten) und bei der Raute (beide Diagonalen).
- Das homogene Quadrat schließlich ist Rechteck und Raute zugleich und weist vier Spiegelsymmetrieachsen auf. Ist es „gefüllt“, kann sich die Anzahl reduzieren, wie die nebenstehende Grafik ebenfalls zeigt.
Kreise und Kreisringe weisen sogar unendlich viele Symmetrieachsen auf, da sie zu jeder Achse durch den Mittelpunkt symmetrisch sind.
Eine weitere Figur mit unendlich vielen Symmetrieachsen ist die Gerade. Da sie unendlich lang ist, ist sie symmetrisch zu jeder zu ihr senkrechten Achse sowie der auf ihr selbst liegenden Achse.

Achsensymmetrie von Funktionsgraphen

Achsensymmetrischer Funktionsgraph

Eine vor allem in der Schulmathematik beliebte Aufgabenstellung besteht darin, für den Graphen einer Funktion die Achsensymmetrie nachzuweisen. Dieser Nachweis ist besonders einfach im Falle der Symmetrie der y-Achse des (kartesischen) Koordinatensystems. Eine Funktion ist achsensymmetrisch zur y-Achse, wenn gilt:

f(-x)\,=\,f(x)

Ist sie für alle x gültig, liegt Achsensymmetrie vor, das heißt f ist eine gerade Funktion.

Diese Bedingung läuft darauf hinaus, dass die Funktionswerte für die entgegengesetzt gleichen Argumente $x$ und $-x$ übereinstimmen müssen.

Allgemeiner gilt: Der Graph einer Funktion f ist genau dann achsensymmetrisch zur Geraden mit der Gleichung $x=a$ , wenn die folgende Bedingung für beliebige Werte von x richtig ist:

f(a-x)\,=\,f(a+x)

Durch Substitution von $x$ mit $x-a$ erhält man die äquivalente Bedingung:

f(2a-x)\,=\,f(x)

Symmetrien lateinischer Großbuchstaben

Symmetrien lateinischer Großbuchstaben

In der Abbildung Symmetrien lateinischer Großbuchstaben sind die 26 Buchstaben nach ihren geometrischen Symmetrieeigenschaften in fünf Gruppen unterteilt. Die Buchstaben FGJLPQR besitzen keine Symmetrie. NSZ sind zweizählig drehsymmetrisch. AMTUVWY sind zu einer vertikalen und BCDEK zu einer horizontalen Spiegelgeraden symmetrisch. Die höchste Symmetrie mit vier Symmetrieelementen weisen die Buchstaben HIOX auf, die sowohl zweizählig drehsymmetrisch sind, als auch jeweils eine horizontale und eine vertikale Spiegelgerade besitzen.

Die Symmetrieeigenschaften von Buchstaben ist hierbei so zu verstehen, dass sie nicht zwangsläufig für jeden Schrifttyp auftreten. So ist beispielsweise das B in vielen Schriftarten nicht spiegelsymmetrisch (etwa als $B$ ), in der hier gewählten Abbildung aber sehr wohl. Generell kann man festhalten, dass bei Kursivschrift sämtliche Spiegelsymmetrien der Buchstaben verloren gehen, die Punktsymmetrien jedoch erhalten bleiben.

Geometrische Symmetrie gibt es auch bei einigen Wörtern. Die Interjektion OHO zum Beispiel hat vier Symmetrieelemente, OTTO hat eine senkrechte und BOB eine waagerechte Spiegelgerade. Diese Wörter sind außerdem Wortpalindrome. DECKE und HEIDE sind spiegelsymmetrisch zu einer horizontalen Geraden.

Punktsymmetrie

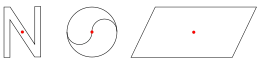
Punktsymmetrische Objekte in der Ebene

Die Punktsymmetrie, auch Zentralsymmetrie,[4] ist eine Eigenschaft geometrischer Objekte. Ein geometrisches Objekt (z. B. ein Viereck) heißt (in sich) punktsymmetrisch, wenn es eine Punktspiegelung gibt, die dieses Objekt auf sich abbildet. Der Punkt, an dem diese Spiegelung erfolgt, wird als Symmetriezentrum bezeichnet.

Beispiele

Bei einem Viereck liegt Punktsymmetrie (in sich) genau dann vor, wenn es sich um ein Parallelogramm handelt. Das Symmetriezentrum ist in diesem Fall der Schnittpunkt seiner Diagonalen. Als Sonderfälle des Parallelogramms sind auch Rechteck, Raute und Quadrat punktsymmetrisch.
Jeder Kreis ist (in sich) punktsymmetrisch zu seinem Mittelpunkt.
Zwei Kreise mit gleichem Radius sind zueinander punktsymmetrisch. Das Symmetriezentrum ist der Mittelpunkt der Verbindungsstrecke zwischen den beiden Kreismittelpunkten. Bei der Punktsymmetrie sind zueinander symmetrische Strecken immer gleich lang.

Punktsymmetrie von Funktionsgraphen

Punktsymmetrischer Funktionsgraph

Eine vor allem in der Schulmathematik häufige Aufgabenstellung besteht darin nachzuweisen, dass der Graph einer gegebenen Funktion punktsymmetrisch ist. Dieser Nachweis kann mit der folgenden Formel geführt werden:

f(a+x)-b=-f(a-x)+b

.

Ist diese Gleichung für alle x erfüllt, liegt Punktsymmetrie zum Punkt (a,b) vor. Im Spezialfall von Punktsymmetrie um dem Ursprung (0,0) vereinfacht sich diese Gleichung zu:

f(-x)=-f(x)

.

Ist sie für alle x gültig, dann liegt Punktsymmetrie in Bezug auf den Koordinatenursprung vor.

Translationssymmetrie

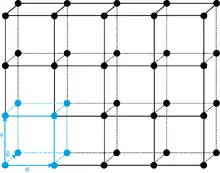
Translationssymmetrisches Gitter

Figuren, die durch eine Verschiebung oder Translation (die nicht die Identität ist) in sich selbst überführt werden, haben eine Translationssymmetrie. Sie werden auch als periodisch bezeichnet.

Figuren, die translationssymmetrisch sind, müssen zwangsläufig unbeschränkt sein. In Anwendungen der Mathematik ist dies praktisch nie gegeben, daher bezeichnet man dort auch beschränkte Teilmengen von periodischen Mengen (Gitter, Kristallstruktur u. Ä.) als periodisch.
Eine Funktion $f\colon X\to Y$ ist translationsinvariant, wenn es einen Vektor ${\vec {a}}\in X$ gibt mit $f({\vec {x}})=f({\vec {x}}-{\vec {a}})$ für alle ${\vec {x}}\in X$ .
Die Schaubilder periodischer reeller Funktionen wie der Sinus-Funktion weisen eine Translationssymmetrie in einer Richtung auf.

In einem Gitter mit den Basisvektoren ${\vec {\alpha }},{\vec {\beta }},{\vec {\gamma }}$ kann durch den Translationsvektor ${\vec {T}}$ jeder Punkt durch ganzzahlige Werte von $u,v,w$ erreicht werden. Der Winkel zwischen ${\vec {\alpha }},{\vec {\beta }},{\vec {\gamma }}$ ist dabei beliebig. Die Basisvektoren sind ebenso Transaltionsvektoren und spannen zusammen die sogenannte Einheitszelle auf.[5]

{\vec {T}}=u*{\vec {\alpha }}+v*{\vec {\beta }}+w*{\vec {\gamma }}

Skalensymmetrie

In manchen mathematischen und physikalischen Zusammenhängen wird die Unveränderbarkeit eines Objekts unter Vergrößerung oder Verkleinerung als Skalensymmetrie oder Skaleninvarianz bezeichnet. Sehr deutlich wird dieses Phänomen bei den sogenannten Fraktalen.

Farbtauschsymmetrie

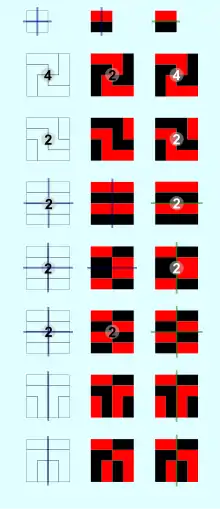
Beispiele farbtauschsymmetrischer Paare

Beispiele klassisch-symmetrischer und autofarbtauschsymmetrischer Figuren

Eine weitere geometrische Symmetrie ist die Farbtauschsymmetrie. Man kann Drehungen und Spiegelungen mit einem Farbtausch kombinieren. Wie zuvor ausgeführt können zwei unterschiedliche Figuren zueinander symmetrisch sein. Symmetrie ist in diesem Fall eine Relation von zwei Objekten. Das gilt auch für die Farbtauschsymmetrie. Besitzt dagegen eine einzelne Figur Farbtauschsymmetrien, so ist sie autofarbtauschsymmetrisch. Autofarbtauschsymmetrisch ist eine Figur, die nach Drehungen und/oder Spiegelungen und einem anschließenden Farbtausch (oder umgekehrt) wieder genau so ausschaut wie vorher.[6]

Die Grafik „Beispiele farbtauschsymmetrischer Paare“ zeigt jeweils zwei farbtauschsymmetrische Figuren. Die „klassischen“ Symmetrien, Zähligkeit und Spiegelsymmetriegeraden, sind, so vorhanden, in die Figuren eingezeichnet. Die Art und Anzahl der Symmetrien sind bei einem Paar farbtauschsymmetrischer Figuren gleich. Nur das in der Grafik unterste Paar besitzt keine solche Symmetrien. Autofarbtauschsymmetrisch ist keine dieser Figuren. Als „Positive“ und „Negative“ sollte man die beiden Figuren eines Paars nicht bezeichnen, da diese Termini durch die Fotografie anderweitig belegt sind. Auch mit Komplementärfarben hat der Farbtausch nichts zu tun.

Im einfachen Fall einer zweifarbigen Figur, und auf diese wollen wir uns hier beschränken, gibt es zwei Voraussetzungen, dass sie überhaupt autofarbtauschsymmetrisch sein kann. Entfernt man die Farben muss die Figur der Umrisse zum einen symmetrisch sein. Zum anderen müssen die Teilbereiche, die die unterschiedlichen Farben einnehmen, kongruent und damit flächengleich sein.

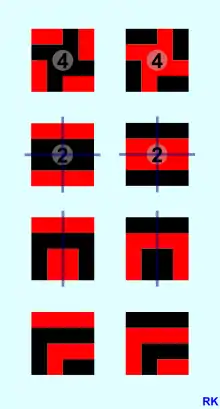
Die Grafik „Beispiele klassisch-symmetrischer und autofarbtauschsymmetrischer Figuren“ zeigt drei Säulen von 7 Figuren, die entstehen, wenn vier Quadrate des kleinen Quadrats oben zu einem größeren Quadrat zusammengefügt und dabei speziell gedreht werden. Das trifft auch auf die Figuren der ersten Grafik zu. Für jede Figur sind ihre Symmetrieelemente, die Zähligkeit bei Rotationssymmetrie und die Spiegelsymmetriegeraden, eingezeichnet.

Die erste und zweite Säule zeigen die Umrisse der Farbflächen bzw. die Farbflächen und deren „klassische“ Symmetrien. Die Zähligkeit ist mit einer schwarzen 4 bzw. 2 markiert, die Spiegelsymmetriegeraden haben die Farbe blau. Die beiden unteren Figuren und die sechste Figur (von unten gezählt) der mittleren Säule besitzen keine „klassischen“ Symmetrien, aber Farbtauschsymmetrien.

In die Figuren der dritten Säule sind die Farbtauschsymmetrien eingezeichnet. Jede Symmetrieoperation entsteht aus zwei Operationen, der Drehung bzw. Spiegelung und gleichzeitig aus einem Austausch der Farben. Die Zähligkeit ist mit einer weißen 4 bzw. 2 markiert, die Farbtauschspiegelsymmetriegeraden haben die Farbe grün. Wie man sieht, verteilen sich die Symmetrien der Umrissfiguren auf „klassische“ und Farbtauschsymmetrien.

Symmetrien im Dreidimensionalen

Nur die mediane Sagittalebene (Medianebene) des Körpers der Bilateria ist eine Spiegelebene

In der Natur

Symmetrie der Stachelhäuter (Pentamerie) am Beispiel des Seesterns: fünfzählige Drehachse und vertikale Spiegelebenen (Punktgruppe C_5v nach Schoenflies)

Der Körperbau der weitaus meisten Tierarten sowie der Aufbau vieler Pflanzenorgane ist äußerlich annähernd spiegelsymmetrisch – in der Biologie als bilateralsymmetrisch bezeichnet – mit einer linken und einer rechten Hälfte. Die einzige Symmetrieebene (Monosymmetrie) ist die anatomische Medianebene, d. h. die mediane (mittig gelegene) Sagittalebene; das ist jede Ebene durch den Körper, die sich von vorne nach hinten und von oben nach unten erstreckt. 95 Prozent aller Tierarten, darunter der Mensch, sind Bilateria („Zweiseitentiere“) mit der namensgebenden Körpersymmetrie (bei den übrigen, sehr ursprünglichen Tieren (z. B. Quallen) findet sich oft Rotationssymmetrie bzgl. einer Längsachse, ihre Körper ist somit ein angenäherter Rotationskörper). Aufgrund der Monosymmetrie der Bilateria lassen sich eindeutige Ebenen und Richtungen des Körpers definieren, was eine anatomische Beschreibung vereinfacht. Doch die Symmetrie des Körpers ist nicht vollkommen, so sind viele einfach vorkommende (unpaare) innere Organe (z. B. Herz) von der Spiegelsymmetrie ausgenommen. Auch alle symmetrisch ausgebildeten Körperteile, beispielsweise beim Menschen Augen, Ohren, Arme, Beine, Brüste usw., weisen zueinander jeweils geringfügige Abweichungen in Lage, Form und Größe auf.

In der Zoologie wird die innerhalb der Bilateria einzigartige fünfstrahlige Radiärsymmetrie der Stachelhäuter als Pentamerie bezeichnet (d. h. beim Seestern verlaufen fünf Symmetrieebenen durch die zentrale Drehachse). In der Mathematik kann man die Symmetrieeigenschaften des Seesterns durch eine Drehgruppe beschreiben. (Die Larven des Seesterns sind noch zweiseitig symmetrisch, wie die meisten anderen Tiere der Gruppe auch. Erst während der Metamorphose entwickelt sich die Pentamerie.)

Ohne eine Symmetrie, d. h. asymmetrisch, sind die Gewebelosen (Schwämme und Placozoa).

Entsprechungen zu zweidimensionalen Symmetrieelementen

Der Achsensymmetrie im Zweidimensionalen entspricht die Spiegelsymmetrie bzgl. einer Ebene im Dreidimensionalen. Der Punktsymmetrie im Zweidimensionalen entspricht die Achsensymmetrie (Drehsymmetrie um 180°). Daneben gibt es noch die Punkt-/ Zentralsymmetrie im Raum und wie in der Ebene Translationssymmetrien.

Rotationssymmetrie / Drehsymmetrie

Reguläre Prismen mit Rotationsachsen und deren Zähligkeiten (n=1 bedeutet: ohne Drehsymmetrie)

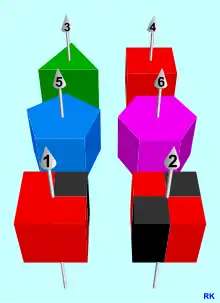
Dreidimensionale Objekte sind rotationssymmetrisch in engeren Sinn, wenn eine Drehung um jeden beliebigen Winkel um eine Achse (die Symmetrieachse) das Objekt auf sich selbst abbildet. Diese Art Rotationssymmetrie um eine Achse wird auch als Zylindersymmetrie bezeichnet. Dreidimensionale geometrische Objekte mit dieser Eigenschaft nennt man auch Rotationskörper.

Analog zum Zweidimensionalen wird der Begriff der Rotations- oder Drehsymmetrie auch angewendet, wenn der Körper durch Drehung um gewisse Winkel um eine Achse auf sich selbst abgebildet werden kann. Als Beispiele für rotationssymmetrische 3D-Objekte sind in der nebenstehenden Grafik Prismen perspektivisch dargestellt, die entstehen, wenn die 2D-Polygone der obigen Grafik Vier reguläre Polygone und zwei weitere geometrische Figuren mit den Kennzahlen ihrer Rotationssymmetrie längs einer senkrecht zur Figur liegenden Geraden im Raum verschoben werden. Bei dieser Vorgehensweise spricht man auch von einer Extrusion des Polygons. Es entstehen gerade Prismen, spezielles Polyeder, die in diesem Fall, wenn die gegebenen Polygone reguläre Polygone sind, reguläre Prismen genannt werden.

Das Symmetriezentrum eines 2D-Objekts wird durch die Extrusion zur Rotationsachse mit einer Pfeilspitze, durch die festgelegt werden kann, ob der Drehwinkel positiv oder negativ zu zählen ist (vgl. Korkenzieherregel). Die dargestellten Symmetrien gehören zu den zyklischen Gruppen $C_{1}$ bis $C_{6}$ und sind Untergruppen der jeweils vollen Symmetriegruppen der Prismen. Es ist zu beachten, dass diese 3D-Objekte weitere Rotations- und Spiegelsymmetrien besitzen. Stellvertretend für die sechs abgebildeten regulären Prismen werden im folgenden Abschnitt alle Rotationssymmetrien eines homogenen Würfels betrachtet.

Drehsymmetrien eines Würfels

Alle 13 Achsen der Rotationssymmetrie eines homogenen Würfels

Drei 4-zählige Achsen

Vier 3-zählige Achsen

Sechs 2-zählige Achsen

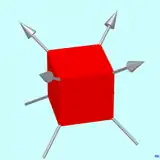
Ein homogener Würfel besitzt insgesamt 13 Drehachsen (Achsen der Rotationssymmetrie), wie in der nebenstehenden Grafik dargestellt:

3 die durch die Mittelpunkte gegenüberliegender Flächen,
4 die durch gegenüberliegende Ecken und
6 die durch die Mittelpunkte gegenüberliegender Kanten verlaufen.

Zählt man die Symmetrieelemente der Rotationssymmetrie des Würfels, so sind es: Das neutrale Element, je 3 für 4-zählige, je 2 für 3-zählige und je eines für 2-zählige Rotationsachsen. Das sind insgesamt $1+3\cdot 3+4\cdot 2+6\cdot 1=24$ Symmetrieelemente.

Diese 24 Elemente bilden zusammen die Würfel-Drehgruppe. Würfel und reguläres Oktaeder sind duale Platonische Körper und besitzen die gleichen Symmetrien. Deshalb werden die Würfel-Drehgruppe und die Oktaeder-Drehgruppe im Artikel Oktaedergruppe gemeinsam abgehandelt. Kombiniert man die Würfel-Drehgruppe mit der Punktspiegelung am Mittelpunkt des Würfels, so ergeben sich $2\cdot 24=48$ Elemente der vollen Symmetriegruppe des Würfels (s. u.).

Spiegelsymmetrie

Piazza del Popolo mit den beiden (näherungsweise) spiegelsymmetrischen Kirchen Santa Maria di Monte Santo und Santa Maria dei Miracoli (und dem Obelisco Flaminio)

Vier Spiegelebenen von neun insgesamt und eine von 13 Rotationsachsen eines homogenen Würfels

Spiegelsymmetrie wird in zwei Bedeutungen verwendet:

Ein Körper besitzt Spiegelsymmetrie, wenn es eine Ebene gibt und die Spiegelung an dieser Ebene eine Symmetrieoperation des betrachteten Körpers ist. Das betrachtete Objekt ist nach der Spiegelung also deckungsgleich mit sich selber. Die Spiegelsymmetrieebene wird auch einfach als Spiegelebene[7] bezeichnet. In dieser Bedeutung ist die Spiegelsymmetrie ein Automorphismus. In der Mathematik wird als Automorphismus eine Abbildung eines mathematischen Objekts auf sich selbst bezeichnet, bei der Objekt und abgebildetes Objekt nicht unterscheidbar sind.[8]

Zwei Körper nennt man zueinander spiegelsymmetrisch, wenn sie sich nur durch Spiegelung an einer Ebene unterscheiden. Umgangssprachlich spricht man von einer spiegelverkehrten Kopie (oder einem spiegelverkehrten Bild). Auf die Lage der beiden Körper im Raum kommt es dabei nicht an. Es kann also sein, dass zunächst eine Verschiebung und eine Drehung erforderlich sind, bevor eine gemeinsame Spiegelebene gefunden werden kann. Die beiden Kirchen Santa Maria di Monte Santo und Santa Maria dei Miracoli an der Piazza del Popolo in Rom sind (näherungsweise) spiegelsymmetrisch und stehen einander gegenüber, so dass eine Spiegelung möglicherweise ohne Verschiebung möglich wäre. Die Kirchen wären dann auch spiegelsymmetrisch in der oben beschriebenen, ersten Bedeutung des Begriffs. Ein weiteres klassisches Beispiel zweier spiegelsymmetrischer Gebäude sind die als King Charles Court und Queen Anne Court bezeichneten Gebäude der von Christopher Wren erbauten Marineakademie Royal Naval College in Greenwich.

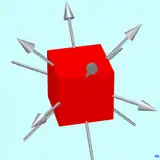
Hochsymmetrische Objekte (wie einige der Prismen in der nebenstehenden Grafik) können sehr viele Spiegelebenen besitzen, die sich alle in einem Punkt schneiden. Eine Kugel hat unendlich viele Spiegelebenen. In der Grafik rechts unten sind vier von neun Spiegelebenen und eine der 13 Rotationsachsen eines homogenen Würfels dargestellt. Die Spiegelebenen schneiden sich in der 4-zähligen Rotationsachse. Die dargestellte Symmetrie ist vom Typ einer Diedergruppe $D_{4}$ und ist eine Untergruppe der Würfelgruppe. Die 48 Symmetrieelemente der Würfelgruppe insgesamt unterteilen den Würfel in 48 (äquivalente) Fundamentalbereiche.

Drehspiegelsymmetrie

Drehspiegelsymmetrie ist die Symmetrie eines Körpers, die sich aus zwei Teiloperationen zusammensetzt. Die erste Teiloperation ist eine Drehung um eine Achse, die Drehspiegelachse, die zweite eine Spiegelung an einer Ebene rechtwinklig zur Drehachse, die Drehspiegelebene.[9] Diese Ebene geht durch das Symmetriezentrum, durch den Mittelpunkt des Körpers. Ist die Drehspiegelebene keine Spiegelsymmetrieebene des Körpers, so sind beide Teiloperationen für sich genommen keine Symmetrieoperationen, sondern nur ihre Kombination. Auf die Reihenfolge der Teiloperationen kommt es dabei nicht an. Wir können auch zuerst die Spiegelung und dann die Drehung ausführen.

Drehspiegelsymmetrien eines Würfels

Ausgewählte Drehspiegelachsen und Drehspiegelebenen eines homogenen Würfels und Wirkung der Drehspiegelung

Eine von drei 4-zähligen Achsen

Eine von vier 6-zähligen Achsen

Eine von sechs 2-zähligen Achsen (Inversion)

Die Drehspiegelung von Körpern auf sich selbst gehört zu den weniger bekannten, aber vielleicht interessantesten Symmetrieoperationen, die man leicht anhand von geeigneten Grafiken nachvollziehen kann. Die drei Grafiken zeigen einen Würfel und jeweils eine der Drehspiegelachsen und ihre zugehörigen Drehspiegelebenen. Um die Drehspiegelebenen von Spiegelsymmetrieebenen zu unterscheiden, werden sie als graue Kreisscheiben dargestellt, die projektiv als Ellipsen erscheinen. Für die Würfel der Grafiken wurde der Zeichenmodus halbtransparent gewählt. Da die Drehspiegelachsen auch Drehachsen sind, werden sie in der Reihenfolge der obigen Grafik Alle 13 Achsen der Rotationssymmetrie ... angeordnet.

Die erste der drei Grafiken zeigt eine der drei 4-zähligen Drehspiegelachsen und die zugehörige Drehspiegelebene. Die Wirkung der Drehspiegelung lässt sich nachvollziehen, wenn man die Bahn der mit einem weißen Punkt markierten Ecke verfolgt. Die Drehspiegelebene ist durch die Drehspiegelachse orientiert. Wir können deshalb sagen, der weiße Punkt liegt oberhalb der Drehspiegelebene. Nach der Drehung um 90° (rechte Handregel: Daumen in Richtung der Achse, Drehung in Richtung der anderen Finger) wird der Punkt zunächst auf die rechte obere Ecke und durch die Spiegelung auf die rechte untere Ecke abgebildet, die durch einen schwarzen Punkt markiert ist. Punkt und Bildpunkt sind durch einen Pfeil verbunden. Die erneute Drehspiegelung um 90° führt zum rechten oberen schwarzen Punkt usw. Nach vierfacher Drehspiegelung ist der Ausgangspunkt wieder erreicht.

Die Bahn eines Punkts des Würfels in allgemeiner Lage ist ein räumlicher, geschlossener Zickzack-Pfad um die Drehspiegelebene. Liegt der Punkt, den wir verfolgen, auf der Drehspiegelebene, ist seine Bahn ein Quadrat. Liegt er auf der Drehspiegelachse, springt er auf der Drehspiegelachse, von der Drehspiegelebene gespiegelt, viermal hin und her. Das Symmetriezentrum, der Schwerpunkt des Würfels, wird stets auf sich selbst abgebildet. Man beachte, dass die Drehspiegelebene in diesem Fall auch eine Spiegelsymmetrieebene des Würfels ist.

Interessant ist der in der zweiten Grafik dargestellte Fall einer von vier 6-zähligen Drehspiegelachsen. Interessant einerseits deshalb, weil die Drehspiegelebene offensichtlich keine Spiegelsymmetrieebene des Würfels ist. Andererseits, weil die 3-zählige Drehachse zur 6-zähligen Drehspiegelachse wird. Dass sie 6-zählig ist, erkennt man wiederum, wenn man die Bahn verfolgt, die ein Punkt des Würfels, zum Beispiel in der Grafik die Bahn der mit einem weißen Punkt markierten Ecke verfolgt. Durch die erste Teiloperation, eine Drehung um 60° um die Drehspiegelachse, wird der weiße Punkt auf einen Punkt abgebildet, der kein Eckpunkt ist. Die zweite Teiloperation, die Spiegelung an der Drehspiegelebene, führt zum ersten Bildpunkt, der als schwarzer Punkt markiert ist und der oberhalb der Drehspiegelebene liegt (schwarzer Punkt rechts oben). Wieder sind Punkt und Bildpunkt mit einem Pfeil verbunden. Wendet man nun die Drehspiegelung um 60° erneut auf den ersten Bildpunkt an, führt das zum zweiten schwarzen Bildpunkt rechts unten usw. Nach 6 Drehspiegelungen um jeweils 60° ist der weiße Ausgangspunkt wieder erreicht. Liegt der Punkt, den wir verfolgen, auf der Drehspiegelebene, ist seine Bahn ein reguläres Sechseck.

Vermutlich unerwartet ist die Wirkung der 2-zähligen Drehspiegelung, der die dritte Grafik gewidmet ist. Dargestellt ist eine der 2-zähligen Drehspiegelachsen, von denen wir, im Analogieschluss von den Drehachsen ausgehend, sechs erwarten. Führen wir die 2-zählige Drehspiegelung nach dem oben skizzierten Vorgehen aus, stellen wir fest, dass jeder Punkt des Würfels auf seinen „Antipoden“ abgebildet wird, auf den Punkt also, der auf der gegenüberliegenden Seite des Würfels liegt. Punkt und Bildpunkt liegen gemeinsam mit dem Symmetriezentrum auf einer Geraden und haben den gleichen Abstand vom Symmetriezentrum. In der Grafik sind in diesem Fall vier weiße Punkte markiert und ihre Bildpunkte als vier schwarze. Alle vier Verbindungsvektoren zwischen Punkt und Bildpunkt schneiden sich im Symmetriezentrum.

Interessant ist auch der Fakt, dass die Drehspiegelungen um alle sechs möglichen 2-zähligen Drehspiegelachsen zum gleichen Symmetrietyp führen. Dieser Symmetrietyp, die Punktspiegelung am Symmetriezentrum, wird in der Gruppentheorie und der Kristallographie Inversion genannt.[10] Man kann daher in Symmetriebetrachtungen alle 2-zähligen Drehspiegelachsen weglassen und sie durch eine einzige Operation, die Inversion, ersetzen.[11]

Eine Drehspiegelung lässt keinen Punkt des Würfels, also keine Ecke, aber auch keine Fläche oder Kante an ihrem ursprünglichen Platz. Einziger Fixpunkt einer Drehspiegelung ist das Symmetriezentrum, der Mittelpunkt des Würfels, worauf bereits hingewiesen wurde.

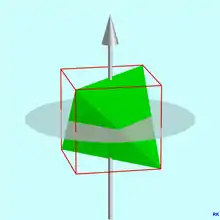
Eine von drei 4-zähligen Drehspiegelachsen mit Drehspiegelebene eines homogenen, regulären Tetraeders

Ein homogenes, reguläres Tetraeder besitzt ebenfalls die 4-zählige Drehspiegelsymmetrie eines homogenen Würfels, wie die Grafik am Beispiel einer Achse zeigt. Wie man aus der Grafik erkennt, ist, im Unterschied zum Würfel, die Drehspiegelebene keine Spiegelsymmetrieebene des Tetraeders. In die Grafik ist auch ein Drahtgittermodell eines umhüllenden Würfels eingezeichnet.

Unterschiede zwischen Drehspiegelung und Drehung

Die Eigenschaften der Drehspiegelungen unterscheiden sich von denen der Drehungen:

Drehachsen eines Körpers können auch Drehspiegelachsen des Körpers sein, aber nicht jede Drehachse ist zwangsläufig eine Drehspiegelachse. Beim Tetraeder zum Beispiel sind dessen 3-zählige Drehachsen keine Drehspiegelachsen.
Das Produkt der Symmetrieoperation einer Drehung mit sich selbst ist stets ein neues Symmetrieelement der Gruppe. Bei einer n-zähligen Drehachse geht die Potenz bis zu (n-1). Das Produkt der Symmetrieoperation einer Drehspiegelachse mit sich selbst ist kein neues Symmetrieelement der Gruppe, sondern eine (einfache) Drehung infolge der zweifachen Spiegelung.
Die Zähligkeiten einer Drehachse und einer gleichgerichteten Drehspiegelachse können gleich sein (beide sind 4-zählig in der ersten Grafik zum Würfel) oder sie können sich unterscheiden (3-zählig bei Drehsymmetrie und 6-zählig bei Drehspiegelsymmetrie in der zweiten Grafik).
Zu jeder Drehspiegelachse eines Würfels gehören zwei Symmetrieelemente pro Drehspiegelachse, unabhängig von ihrer Zähligkeit. Da der Würfel drei 4-zählige und vier 3-zählige Drehspiegelachsen besitzt, gibt es $2\cdot (3+4)=14$ Drehspiegelelemente der Würfelgruppe im engeren Sinne. Hinzu kommt eine Punktspiegelung aller 2-zähligen Drehspiegelachsen, die Inversion, so dass sich 15 Drehspiegelelemente insgesamt ergeben.

Wie eingangs erwähnt ist die Punktspiegelung im Zweidimensionalen gleichbedeutend mit einer Drehung um 180° um den Fixpunkt und somit kein eigenes Symmetrieelement.

Punktsymmetrie / Inversionssymmetrie

Wirkung der Punktspiegelung / Inversion für vier ausgewählte Ecken eines Würfels

Wie im vorangegangenen Abschnitt beschrieben, ist die Punktsymmetrie oder Inversionssymmetrie die Symmetrie eines Körpers bezüglich eines Punkts, des Symmetriezentrums. Jeder Punkt tauscht mit dem Punkt, der auf der Geraden, die von diesem Punkt durch das Zentrum geht und auf der anderen Seite des Zentrums im gleichen Abstand liegt, seine Position. Es handelt sich um eine Punktspiegelung des Körpers auf sich selbst. Die Punktspiegelung, lässt keinen Punkt des Körpers an seinem ursprünglichen Platz, mit einer Ausnahme: Einziger Fixpunkt einer Drehspiegelung ist das Symmetriezentrum, der Mittelpunkt des Körpers.

Die Grafik zeigt die Abbildung von vier ausgewählten Ecken (weiße Punkte) eines Würfels durch Inversion (schwarze Punkte). Umgekehrt werden alle schwarzen Punkte auf die weißen abgebildet. Die Grafik ist eine Wiederholung der dritten obigen Grafik (Ausgewählte Drehspiegelachsen ...) ohne 2-zählige Drehspiegelachse und Drehspiegelebene.

Die homogenen Platonischen Körper Würfel, Oktaeder, Dodekaeder und Ikosaeder sind punktsymmetrisch. Der einfachste Platonische Körper dagegen, das reguläre Tetraeder, ist es nicht.

Im Fall des Würfels hatten sich (einschließlich der Inversion) 15 Drehspiegelsymmetrien ergeben. Zusammen mit den 9 Spiegelebenen ergibt das 24 Symmetrieelemente, also genau so viele, wie es Elemente der Würfel-Drehgruppe gibt. Das ist kein Zufall, denn jedes Spiegel- oder Drehspiegelelement lässt sich als eine Kombination aus einer Drehung und einer Inversion interpretieren. In diesem Sinne besitzt die Inversion eines inversionssymmetrischen Körpers eine ähnlich herausgehobene Stellung wie das neutrale Element innerhalb einer Symmetriegruppe.

Kugelsymmetrie

Rotationssymmetrie um jede beliebige Achse durch denselben Punkt ist ein Spezialfall der Rotationssymmetrie und wird als Kugelsymmetrie bzw. Radialsymmetrie bezeichnet. Sterne sind z. B. annähernd kugelsymmetrisch, da deren Eigenschaften (wie z. B. die Dichte) zwar nicht überall gleich sind, aber nur vom Abstand zum Mittelpunkt abhängen. Auch deren Schwerefelder sowie z. B. das elektrische Feld einer rotationssymmetrisch geladenen Kugel sind kugelsymmetrisch.

Kombinationen

Aus der Möglichkeit, Symmetrieoperationen zu kombinieren, lassen sich die symmetrischen Grundoperationen herleiten:

Identität (Null-Operation, keine Veränderung)
Rotation (Drehung)
Rotation – Inversion (Drehspiegelung)
Translation (Verschiebung)
Gleitspiegelung
Schraubung

Siehe auch

Literatur

Hermann Weyl: Symmetrie: Ergänzt durch den Text „Symmetry and Congruence'“ aus dem Nachlass und mit Kommentaren von Domenico Giulini, Erhard Scholz und Klaus Volkert. Übersetzerin Lulu Hofmann Bechtolsheim. 3. Auflage. Springer Spektrum, Berlin / Heidelberg 2017, ISBN 978-3-662-52711-5 (VII, 232, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 23. Juli 2019]). Reprint des Originals von 1952 in Hermann Weyl: Symmetry. Princeton University Press, Princeton NJ 2015 (176 S., eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 23. Juli 2019]).
H. Schupp: Elementargeometrie. UTB Schöningh 1977, ISBN 3-506-99189-2, S. 35, 45.
Will Kleber et al.: Einführung in die Kristallographie. 19., verbesserte Auflage. Oldenbourg Verlag, München 2010, ISBN 978-3-486-59075-3 (470 S., eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 18. August 2019]).
Werner Hahn: Symmetrie als Entwicklungsprinzip in Natur und Kunst. Mit einem Vorwort von Rupert Riedl. Königstein i. Ts. (Verlag Langewiesche) 1989.
M.I. Voitsekhovskii: Symmetry. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
Arthur Schoenflies: Krystallsysteme und Krystallstructur. Teubner, Leipzig 1891 (XII, 638 S., Textarchiv – Internet Archive).
David Wade: Macht der Symmetrie. Artemis & Winkler Verlag, 2011, ISBN 978-3-538-07311-1

Weblinks

Commons: Symmetrie – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Symmetrie – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Die Terminologie ist nicht immer einheitlich. Man nennt die Rotationssymmetrie um einen festen Winkel auch Drehsymmetrie, um sie von der Rotationssymmetrie zum Beispiel der eines Kreises zu unterscheiden.
Kleber 2010, S. 52
Drehsymmetrie. Abgerufen am 20. November 2019.
Meyers großes Taschenlexikon in 24 Bänden. BI-Taschenbuchverlag 1992, Band 21, S. 258.
Einführung in die Materialwissenschaft I. Abgerufen am 26. September 2020.
Herbert Glaser: Ein Stufenmodell für das Lehren von Abbildungen und des Symmetriebegriffs. In: Der Mathematikunterricht. Band 52, Nr. 3, 2006, S. 15–24.
Spiegelebene. In: Richard Lenk (Hrsg.): Physik. 2. Auflage. Band 2: Ma–Z. Brockhaus, Leipzig 1989, ISBN 3-325-00192-0, S. 909 (Seiten 601–1146, 48 Tafeln).
Der nahe liegende Begriff Autospiegelsymmetrie, der diese Spiegelsymmetrie von der Spiegelsymmetrie in der ersten Bedeutung unterscheiden würde, ist nicht üblich (kein Treffer bei Google).
Kleber 2010, S. 60 ff.
Man beachte, dass der Name Inversion auch für die Spiegelung an einem Kreis benutzt wird.
Schoenflies weist auf Seite 90 seiner Monographie darauf hin, dass man die zweizähligen Spiegelsymmetrieachsen, die er zweizählige Symmetrieaxen zweiter Art nennt, weglassen und nur von Inversion sprechen sollte: „Diejenige Operation, welche für die zweizählige Symmetrieaxe zweiter Art characteristisch ist, ist die Inversion, die Axe stellt daher dieselbe Symmetrieeigenschaft dar, wie ein Centrum der Symmetrie. Für ein Symmetriecentrum giebt es aber keinerlei ausgezeichnete Richtung mehr, jede zweizählige Axe zweiter Art ist ihm äquivalent. Aus diesem Grunde ist es angezeigt, die Axen zweiter Art ganz aus dem Spiele zu lassen; es könnte sich sonst leicht die irrthümliche Auffassung bilden, dass auch für sie die durch die Axe repräsentirte Richtung eine besondere Bedeutung für die bezügliche Symmetrieeigenschaft hat.“

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Die Terminologie ist nicht immer einheitlich. Man nennt die Rotationssymmetrie um einen festen Winkel auch Drehsymmetrie, um sie von der Rotationssymmetrie zum Beispiel der eines Kreises zu unterscheiden.

[2] Kleber 2010, S. 52

[3] Drehsymmetrie. Abgerufen am 20. November 2019.

[meyers-4] Meyers großes Taschenlexikon in 24 Bänden. BI-Taschenbuchverlag 1992, Band 21, S. 258.

[5] Einführung in die Materialwissenschaft I. Abgerufen am 26. September 2020.

[6] Herbert Glaser: Ein Stufenmodell für das Lehren von Abbildungen und des Symmetriebegriffs. In: Der Mathematikunterricht. Band 52, Nr. 3, 2006, S. 15–24.

[Physik2_1989-7] Spiegelebene. In: Richard Lenk (Hrsg.): Physik. 2. Auflage. Band 2: Ma–Z. Brockhaus, Leipzig 1989, ISBN 3-325-00192-0, S. 909 (Seiten 601–1146, 48 Tafeln).

[8] Der nahe liegende Begriff Autospiegelsymmetrie, der diese Spiegelsymmetrie von der Spiegelsymmetrie in der ersten Bedeutung unterscheiden würde, ist nicht üblich (kein Treffer bei Google).

[9] Kleber 2010, S. 60 ff.

[10] Man beachte, dass der Name Inversion auch für die Spiegelung an einem Kreis benutzt wird.

[11] Schoenflies weist auf Seite 90 seiner Monographie darauf hin, dass man die zweizähligen Spiegelsymmetrieachsen, die er zweizählige Symmetrieaxen zweiter Art nennt, weglassen und nur von Inversion sprechen sollte: „Diejenige Operation, welche für die zweizählige Symmetrieaxe zweiter Art characteristisch ist, ist die Inversion, die Axe stellt daher dieselbe Symmetrieeigenschaft dar, wie ein Centrum der Symmetrie. Für ein Symmetriecentrum giebt es aber keinerlei ausgezeichnete Richtung mehr, jede zweizählige Axe zweiter Art ist ihm äquivalent. Aus diesem Grunde ist es angezeigt, die Axen zweiter Art ganz aus dem Spiele zu lassen; es könnte sich sonst leicht die irrthümliche Auffassung bilden, dass auch für sie die durch die Axe repräsentirte Richtung eine besondere Bedeutung für die bezügliche Symmetrieeigenschaft hat.“