Internationales Einheitensystem

Das Internationale Einheitensystem oder SI (französisch Système international d’unités) ist das am weitesten verbreitete Einheitensystem für physikalische Größen. Die durch das SI definierten Maßeinheiten nennt man SI-Einheiten.

Das SI beruht auf sieben Basisgrößen mit entsprechenden Basiseinheiten, deren Auswahl nach praktischen Gesichtspunkten erfolgte. Seit 2019 sind alle SI-Einheiten über Naturkonstanten definiert.[A 1]

Das SI ist ein metrisches Einheitensystem (d. h., eine Basiseinheit ist der Meter), es ist dezimal (d. h., die verschiedenen Einheiten, mit denen man eine Größe angeben kann, unterscheiden sich nur um ganze Zehnerpotenzen) und es ist kohärent (d. h., jede abgeleitete Einheit ist ein Produkt von Potenzen der Basiseinheiten ohne zusätzliche numerische Faktoren).

Verbreitung und Verwendung

Das SI ist in der ganzen Welt verbreitet. In den meisten Industrieländern ist sein Gebrauch für den amtlichen und geschäftlichen Verkehr gesetzlich vorgeschrieben. Ausnahme unter den Industriestaaten sind die USA, wo das SI zwar gilt,[A 2] im amtlichen und geschäftlichen Verkehr aber auch das angloamerikanische Maßsystem (customary units) zugelassen ist.

Neben den SI-Einheiten werden oft weitere Einheiten verwendet, die keine SI-Einheiten sind. Das Internationale Büro für Maß und Gewicht (BIPM) definiert selbst eine Reihe von Einheiten, die „zur Verwendung mit dem SI zugelassen“ sind, z. B. Hektar, Liter, Minute, Stunde und Winkelgrad. Darüber hinaus gibt es landesspezifisch weitere gesetzlich zugelassene Einheiten, meist für spezielle Zwecke. In der Europäischen Union und der Schweiz sind dies z. B. Tex und Dioptrie.[1]

In einigen Bereichen sind vom SI abweichende Einheiten gebräuchlich und meist auch amtlich zugelassen: In der Schiff- und Luftfahrt werden nicht-SI-konforme Einheiten für Flughöhe (Fuß), Entfernungen (Seemeile) und Geschwindigkeiten (Knoten)[2] verwendet. In Teilgebieten der Physik sind unterschiedliche natürliche Einheiten gebräuchlich, in der Elektrodynamik teilweise noch das Gauß’sche CGS-System.

Zuständigkeiten

Internationale Regelungen

Für internationale Regelungen zum SI sind das Internationale Büro für Maß und Gewicht (Bureau International des Poids et Mesures, BIPM) und dessen Generalkonferenz für Maß und Gewicht (Conférence Générale des Poids et Mesures, CGPM) zuständig. Als Referenz-Regelwerk gilt die vom BIPM publizierte Broschüre Le Système international d’unités – deutsch kurz als „die SI-Broschüre“ bezeichnet. Die 9. Auflage der SI-Broschüre erschien 2019.[3][4]

Nationale Umsetzung

Für die nationale Umsetzung des SI sind meist die metrologischen Staatsinstitute zuständig. Dies sind zum Beispiel

in Deutschland die Physikalisch-Technische Bundesanstalt (PTB) (in der DDR war es das Amt für Standardisierung, Meßwesen und Warenprüfung [ASMW]),
in der Schweiz das Eidgenössische Institut für Metrologie (METAS),
in Österreich das Bundesamt für Eich- und Vermessungswesen (BEV),
in Großbritannien das National Physical Laboratory (NPL) und
in den USA das National Institute of Standards and Technology (NIST).

Eine Anwendungspflicht des SI entsteht erst durch Gesetze oder Rechtsprechung einzelner Staaten.

Gesetze, die die Einführung des SI regelten, traten 1970 in der Bundesrepublik Deutschland (Einheiten- und Zeitgesetz), 1973 in Österreich (Maß- und Eichgesetz), 1974 in der DDR und 1978 in der Schweiz in Kraft; 1978 waren alle Übergangsregelungen betreffend Nicht-SI-Einheiten abgeschlossen.

In der EU ist die Verwendung von Einheiten im Bereich des gesetzlichen Messwesens unter anderem durch die Richtlinie 80/181/EWG weitgehend vereinheitlicht worden. In der Europäischen Union, der Schweiz und den meisten anderen Staaten ist die Benutzung des SI im amtlichen oder geschäftlichen Verkehr gesetzlich vorgeschrieben. Mit der Richtlinie 2009/3/EG[5][6] wurde die Verwendung von zusätzlichen Einheiten in der EU unbefristet erlaubt (durch vorhergehende Richtlinien war dies ursprünglich nur bis zum 31. Dezember 2009 möglich). Dies wird hauptsächlich damit begründet, Exporte von Waren in Drittländer nicht zu behindern.

SI-Einheiten

Der Begriff „SI-Einheit“ umfasst alle im SI definierten Einheiten: die Basiseinheiten und die abgeleiteten Einheiten, ohne und mit SI-Präfix.[7][8]

SI-Basiseinheiten

Die sieben Einheiten „Sekunde“ (s), „Meter“ (m), „Kilogramm“ (kg), „Ampere“ (A), „Kelvin“ (K), „Mol“ (mol) und „Candela“ (cd) wurden im SI in dieser Reihenfolge als Basiseinheiten festgelegt, passend zu den entsprechenden Basisgrößen des zu Grunde liegenden Internationalen Größensystems (ISQ). Jede Größe kann als Kombination der Basisgrößen ausgedrückt werden, aber definitionsgemäß kann keine Basisgröße von den anderen abgeleitet werden. Analog dazu können alle SI-Einheiten auf genau eine Weise durch die Basiseinheiten ausgedrückt werden. Die Basisgrößen und ‑einheiten wurden von der CGPM nach praktischen Gesichtspunkten ausgewählt. Bis zur Reform von 2019 basierte das SI auf den Definitionen der sieben Basiseinheiten.

Jeder Basisgröße wird eine Dimension mit demselben Namen zugeordnet. Beispielsweise heißt die Dimension der Basisgröße Länge ebenfalls Länge. Das Symbol der Größe wird mit einem kursiv geschriebenen Buchstaben „l“ bezeichnet; jenes der Dimension mit einem aufrecht stehenden, großgeschriebenen Buchstaben „L“. Die praktische Realisierung einer Dimension erfolgt durch eine entsprechende kohärente Einheit – im Falle der Länge durch den Meter.

Basisgröße und Dimensionsname	Größen- symbol	Dimensions- symbol	Einheit	Einheiten- zeichen
Zeit	t	T	Sekunde	s
Länge	l	L	Meter	m
Masse	m	M	Kilogramm	kg
Stromstärke	I	I	Ampere	A
Thermodynamische Temperatur	T	Θ	Kelvin	K
Stoffmenge	n	N	Mol	mol
Lichtstärke	I_v	J	Candela	cd

Abgeleitete Größen und Einheiten

Alle physikalischen Größen außer den oben genannten sieben Basisgrößen des ISQ sind abgeleitete Größen. Jede physikalische Größe Q (für engl. quantity) hat eine Dimension, die eindeutig als Potenzprodukt der Dimensionen der sieben Basisgrößen dargestellt werden kann:

dim Q = T^α · L^β · M^γ · I^δ · Θ^ε · N^ζ · J^η

Jeder der Dimensionsexponenten α, β, γ, δ, ε, ζ und η ist entweder Null oder eine positive oder negative, im Allgemeinen ganze Zahl. Der Betrag des Exponenten liegt in der Regel zwischen 0 und 4.

Entsprechend können die zugehörigen abgeleiteten SI-Einheiten als Produkt aus einem numerischen Faktor k und dem Potenzprodukt der Basiseinheiten ausgedrückt werden:

[Q] = k · s^α · m^β · kg^γ · A^δ · K^ε · mol^ζ · cd^η

„[Q]“ stellt dabei symbolisch den Ausdruck „die Einheit der Größe Q“ dar. Wie im Folgenden erklärt, ist das SI so konstruiert, dass k immer eine ganzzahlige Zehnerpotenz ist.

Kohärente Einheiten

Ist der numerische Faktor k gleich eins, so liegt eine kohärente SI-Einheit vor.[7][8] Da jede physikalische Größe eine eindeutig definierte Dimension hat, hat sie genau eine kohärente SI-Einheit. Unterschiedliche physikalische Größen mit derselben Dimension haben auch dieselbe kohärente Einheit. Beispiele:

Meter pro[A 3] Sekunde (m/s) ist die kohärente SI-Einheit der abgeleiteten Größe „Geschwindigkeit“.
Ampere (A) ist die kohärente SI-Einheit der Basisgröße „elektrische Stromstärke“ und der abgeleiteten Größe „magnetische Durchflutung“.

Abgeleitete SI-Einheiten mit besonderem Namen

Für 22 abgeleitete SI-Einheiten wurden eigene Namen und Einheitenzeichen (Symbole) definiert. Diese können selbst wieder mit allen Basis- und abgeleiteten Einheiten kombiniert werden. So eignet sich zum Beispiel die SI-Einheit der Kraft, das Newton, um das Joule, die Einheit der Energie, als Newton mal Meter (N·m) auszudrücken. Diese Namen dürfen aber nur für jeweils die zugeordneten Größen verwendet werden, nicht für andere Größen derselben Dimension. Zum Beispiel wird das Drehmoment in Newton mal Meter angegeben, nicht aber in Joule.

Alle diese Einheiten sind kohärent; bestehende inkohärente metrische Einheiten mit eigenem Namen (Liter, Bar, …) wurden nicht ins SI übernommen. Dies hat den großen Vorteil, dass in physikalischen und technischen Formeln keine Umrechnungsfaktoren zwischen den Einheiten benötigt werden. Beispielsweise gilt einfach 1 J = 1 N·m = 1 C·V = 1 W·s.

Größe^a)	Einheit	Einheiten- zeichen	in anderen SI-Einheiten ausgedrückt	in SI-Basis- Einheiten aus- gedrückt^a)
ebener Winkel	Radiant^b)	rad	m/m	1
Raumwinkel	Steradiant^b)	sr	m²/m²	1
Frequenz	Hertz	Hz		s⁻¹
Kraft	Newton	N	J/m	kg · m · s⁻²
Druck	Pascal	Pa	N/m²	kg · m⁻¹ · s⁻²
Energie, Arbeit, Wärmemenge	Joule	J	N · m; W · s	kg · m² · s⁻²
Leistung	Watt	W	J/s; V · A	kg · m² · s⁻³
elektrische Ladung	Coulomb	C		A · s
elektrische Spannung	Volt	V	W/A; J/C	kg · m² · s⁻³ · A⁻¹
elektrische Kapazität	Farad	F	C/V	kg⁻¹ · m⁻² · s⁴ · A²
elektrischer Widerstand	Ohm	Ω	V/A	kg · m² · s⁻³ · A⁻²
elektrischer Leitwert	Siemens	S	A/V	kg⁻¹ · m⁻² · s³ · A²
magnetischer Fluss	Weber	Wb	V · s	kg · m² · s⁻² · A⁻¹
magnetische Flussdichte	Tesla	T	Wb/m²	kg · s⁻² · A⁻¹
Induktivität	Henry	H	Wb/A	kg · m² · s⁻² · A⁻²
Celsius-Temperatur^c)	Grad Celsius^c)	°C		K
Lichtstrom	Lumen	lm	cd · sr	cd
Beleuchtungsstärke	Lux	lx	lm/m²	cd · m⁻²
Radioaktivität	Becquerel	Bq		s⁻¹
Energiedosis	Gray	Gy	J/kg	m² · s⁻²
Äquivalentdosis	Sievert	Sv	J/kg	m² · s⁻²
katalytische Aktivität	Katal	kat		mol · s⁻¹

^a) Reihenfolge gemäß der SI-Broschüre[3]

^b) Radiant (rad) und Steradiant (sr) können und werden üblicherweise statt der Einheit 1 für den ebenen Winkel bzw. den Raumwinkel verwendet, um die Bedeutung des dazugehörigen Zahlenwertes hervorzuheben.

^c) Die Celsius-Temperatur t ist als die Differenz t = T−T₀ zwischen den beiden thermodynamischen Temperaturen T und T₀ definiert, wobei T₀ = 273,15 K.[6][9]

SI-Präfixe

Aus praktischen Gründen bietet das SI zu allen Größen weitere Einheiten an, die sich von den kohärenten Einheiten um Zehnerpotenzen mit ganzzahligem Exponenten unterscheiden. Sie werden durch Präfixe wie Kilo- (10³) oder Milli- (10⁻³) bezeichnet.

Bis 2018: Separat definierte Basiseinheiten

Bis 2018 hatte jede der sieben Basiseinheiten ihre eigene Definition: „Die Basiseinheit X ist …“ Davon wurden alle anderen Einheiten abgeleitet. Diese Definitionen wurden mit dem fortschreitenden Stand der Messtechnik sowie nach revidierten prinzipiellen Überlegungen mehrfach geändert. So wurde zum Beispiel der Meter ab 1889 anhand eines Prototyps („Urmeter“) und ab 1960 anhand einer speziellen Lichtwellenlänge definiert. Mit der Definition war dadurch zugleich die Realisierung vorgegeben, wobei einige Realisierungen von anderen Basiseinheiten abhingen (z. B. war die Temperatur vorgegeben, bei der die Länge des Meterprototypen gemessen werden sollte). Wenn besser geeignete Verfahren zur Realisierung entwickelt wurden, musste für deren Verwendung die Definition der entsprechenden Basiseinheit geändert werden.

Seit 2019: Definition über physikalische Konstanten

Konstante		exakter Wert[10]		seit
Δν_Cs	Strahlung des Caesium-Atoms[A 4]	9 192 631 770	Hz	1967
c	Lichtgeschwindigkeit	299 792 458	m/s	1983
h	Plancksches Wirkungsquantum	6.62607015e^-34	J·s	2019
e	Elementarladung	1.602176634e^-19	C	2019
k_B	Boltzmann-Konstante	1.380649e^-23	J/K	2019
N_A	Avogadro-Konstante	6.02214076e²³	mol⁻¹	2019
K_cd	Photometrisches Strahlungsäquivalent*	683	lm/W	1979
* für monochromatische Strahlung der Frequenz 540 THz (grünes Licht)

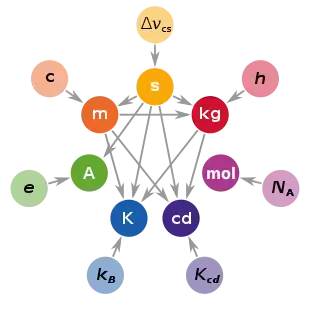
Ableitung der SI-Basiseinheiten von den exakt festgelegten Konstanten[A 1]. Die Pfeile bedeuten dabei jeweils „… wird zur Definition von … verwendet“ (siehe aber Anmerkung[A 5]).

Im November 2018 beschloss die 26. Generalkonferenz für Maß und Gewicht eine grundlegende Revision, die am 20. Mai 2019, dem Weltmetrologietag, in Kraft trat: Nachdem zuvor schon drei der Basiseinheiten (s, m, cd) dadurch definiert gewesen waren, dass man drei physikalischen Konstanten (Δν_Cs, c, K_cd) einen festen Wert zugewiesen hatte, bekamen nun weitere vier Konstanten feste Werte.[A 1] Seitdem ist keine SI-Einheit mehr von Artefakten oder Werkstoffeigenschaften abhängig.[A 4]

Zugleich wurde das Grundprinzip geändert: Seit der Reform lauten die sieben grundlegenden Definitionen jeweils sinngemäß: „Die Konstante X hat den Zahlenwert Y, wenn man sie in kohärenten SI-Einheiten ausdrückt.“[10] Hieraus können alle SI-Einheiten gleichermaßen abgeleitet werden; es gibt keinen prinzipiellen Unterschied mehr zwischen Basiseinheiten und abgeleiteten Einheiten.[11][A 6] Der Begriff „Basiseinheit“ wird jedoch weiterhin verwendet, da es sich als nützlich erwiesen hat, einheitlich dieselben sieben Dimensionen und deren kohärente Einheiten zu verwenden.[12] Die folgende Tabelle gibt an, wie sich diese sieben Einheiten von den sieben definierenden Konstanten ableiten lassen:[13]

Einheit	Definierende Gleichung	unter Verwendung von
Einheit	Definierende Gleichung	explizit	implizit
Sekunde	${\textstyle \Delta \nu _{\mathrm {Cs} }=9\,192\,631\,770\ {\frac {1}{\mathrm {s} }}}$
Meter	${\textstyle c=299\,792\,458\ {\frac {\mathrm {m} }{\mathrm {s} }}}$	s	Δν_Cs
Kilogramm	${\textstyle h=6{,}626\,070\,15\cdot 10^{-34}\ {\frac {\mathrm {kg} \,\mathrm {m} ^{2}}{\mathrm {s} }}}$	s, m	Δν_Cs, c
Ampere	${\textstyle e=1{,}602\,176\,634\cdot 10^{-19}\ \mathrm {A} \,\mathrm {s} }$	s	Δν_Cs
Kelvin	${\textstyle k_{\mathrm {B} }=1{,}380\,649\cdot 10^{-23}\ {\frac {\mathrm {kg} \,\mathrm {m} ^{2}}{\mathrm {s} ^{2}\,\mathrm {K} }}}$	s, m, kg	Δν_Cs, h[A 5]
Mol	${\textstyle N_{\mathrm {A} }=6{,}022\,140\,76\cdot 10^{23}\ {\frac {1}{\mathrm {mol} }}}$
Candela	${\textstyle K_{\mathrm {cd} }=683\ {\frac {\mathrm {cd} \,\mathrm {sr} \,\mathrm {s} ^{3}}{\mathrm {kg} \,\mathrm {m} ^{2}}}}$	s, m, kg	Δν_Cs, h[A 5]

Schreibweisen

Die SI-Broschüre nennt auch Regeln zur Formatierung und Schreibweise von Zahlen, Einheiten und Größen. Einige dieser Regeln wurden von der CGPM beschlossen, andere wurden von der ISO und anderen Organisationen erarbeitet und haben sich als Standard etabliert.

Schreibweise von Zahlen

Das SI lässt zu, dass Zahlen in Gruppen von je drei Ziffern aufgeteilt werden, wobei die Gruppen nicht durch Punkte oder durch Kommata getrennt werden.[14] Als Dezimaltrennzeichen sind sowohl das Komma als auch der Punkt zugelassen;[14] genormt ist im deutschsprachigen Raum allein das Komma.[15]

Schreibweise von Einheiten

Für die Namen der Einheiten sind je nach Sprache unterschiedliche Schreibweisen möglich (Beispiel: dt. Sekunde, engl. second, frz. seconde). Die Einheitennamen unterliegen außerdem der normalen Flexion der jeweiligen Sprache.

Die Zeichen der Einheiten sind international einheitlich. Unabhängig vom Format des umgebenden Textes sind sie in aufrechter Schrift zu schreiben. Groß- und Kleinschreibung sind vorgegeben und können bedeutungsunterscheidend sein (Beispiel: „s“ = Sekunde, „S“ = Siemens). Symbole von Einheiten, die nach einer Person benannt sind, und nur diese, beginnen mit einem Großbuchstaben. Eine Ausnahme ist die Nicht-SI-Einheit Liter: Neben dem klein geschriebenen „l“ darf auch das groß geschriebene „L“ verwendet werden, um Verwechslungen mit der Ziffer „Eins“ zu vermeiden.

Die SI-Präfixe werden unmittelbar vor das Einheitenzeichen der kohärenten Einheit gestellt. Eine Ausnahme bildet das Kilogramm (kg), das nur vom Gramm (g) ausgehend mit SI-Präfixen verwendet werden darf. Beispielsweise muss es für 10⁻⁶ kg „mg“ und nicht „μkg“ heißen.[A 7]

Hinweise auf bestimmte Sachverhalte sollen nicht an Einheitenzeichen angebracht werden; sie gehören zum Formelzeichen der verwendeten physikalischen Größe oder in erläuternden Text. Falsch wäre demnach V_eff als „Einheit“ von Effektivwerten der elektrischen Spannung; korrekt ist die Angabe einer „Effektivspannung“ U_eff in V.

Schreibweise von Größen

Größensymbole (Formelzeichen) können frei gewählt werden – allgemein übliche Formelzeichen wie l, m oder t stellen lediglich Empfehlungen dar. Sie sind in kursiver Schrift zu schreiben. Die Dimensionssymbole der Basisgrößen werden hingegen als aufrecht stehender Großbuchstabe in serifenloser Schrift geschrieben.

Zwischen Zahlenwert und Einheitenzeichen steht kein Multiplikationszeichen, aber ein Leerzeichen – das gilt auch bei Prozent und Grad Celsius. Einzig die Einheitenzeichen °, ′ und ″ für die Nicht-SI-Winkeleinheiten Grad, Minute und Sekunde werden direkt nach dem Zahlenwert ohne Zwischenraum gesetzt. Größenangaben werden wie mathematische Produkte behandelt und unterliegen den Regeln der Multiplikation. Daher kann man z. B. statt „p = 48 kPa“ auch „p/kPa = 48“ schreiben.

Name und Symbol einer physikalischen Größe sollen keinen Bezug zu einer bestimmten Einheit herstellen. Bezeichnungen wie „Literleistung“ sind zu vermeiden.

Geschichte

1790: Die französische Akademie der Wissenschaften erhält von der französischen Nationalversammlung den Auftrag, ein einheitliches System von Maßen und Gewichten zu entwerfen. Sie folgt dabei den Prinzipien, die Grundeinheiten aus naturgegebenen Größen abzuleiten, alle anderen Einheiten darauf zurückzuführen und dezimal zu vervielfachen und zu unterteilen. Als Grundeinheiten werden gewählt:[16]

der Meter als zehnmillionster Teil des Erdmeridianquadranten,
das Grave (später: „Kilogramm“) als Gewicht (später als Masse) von 1 dm³ reinem Wasser bei maximaler Dichte (ca. 4 °C).

1832: Carl Friedrich Gauß entwickelt, in der Folge gemeinsam mit Wilhelm Weber, ein System „absoluter“ elektromagnetischer Einheiten basierend auf Länge (mm), Masse (g) und Zeit (s) mit gebrochenen Exponenten.

1861: Ausgehend von den Arbeiten von Gauß und Weber definiert die British Association for the Advancement of Science (BAAS) elektromagnetische Einheiten mit den Basiseinheiten m (später cm), g, s. Wegen der Unhandlichkeit dabei erhaltener Einheiten werden zusätzlich Einheiten eingeführt, die dezimale Vielfache der Grundeinheiten sind, insbesondere das Volt als 10⁸ und das Ohm als 10⁹ elektromagnetische cgs-Einheiten. In den folgenden Jahrzehnten etablieren sich diese Einheiten weltweit. 1894 werden die Realisierungen dieser Einheiten international vereinheitlicht und zu deren Definition verwendet.

1873: James Clerk Maxwell schlägt vor, die Einheiten von Länge, Zeit und Masse über die Wellenlänge und Periodendauer von Licht sowie die Masse von Molekülen zu definieren.[17]

1875: Die Meterkonvention wird von 17 Staaten unterzeichnet. Das Internationale Büro für Maß und Gewicht wird gegründet.

1889: Auf der ersten Generalkonferenz für Maß und Gewicht (CGPM) werden die angefertigten Urmaße für den Meter und das Kilogramm anerkannt.[18] Zusammen mit der Sekunde werden diese in den folgenden Jahren die Basis mehrerer Einheitensysteme, insbesondere MKS und CGS.

1900: Max Planck schlägt vor, Basiseinheiten durch physikalische „Constanten“ zu definieren.[19]

1901: Giovanni Giorgi zeigt, dass man die mechanischen und elektrischen Einheiten zu einem kohärenten System mit ganzzahligen Exponenten zusammenführen kann, indem man das MKS-System um eine vierte Basisgröße erweitert und die Gleichungen der Elektrodynamik umformuliert.[20] Dieser Vorschlag erhält in den 1930er Jahren Unterstützung durch die Internationale elektrotechnische Kommission (IEC)[21] und die Internationale Union für Reine und Angewandte Physik (IUPAP). Das zuständige Komitee des BIPM empfiehlt das Ampere als vierte Basiseinheit.[22]

1948: Die 9. CGPM beauftragt das Internationale Komitee (CIPM), die Grundlagen für ein einheitliches, „praktisches“ Einheitensystem zu erarbeiten.[23] Das Ampere wird in der bis 2019 gültigen Form definiert. Regeln zur Schreibweise werden festgelegt.[24]

1954: Basierend auf der Arbeit des CIPM beschließt die 10. CGPM ein System mit sechs Basiseinheiten. Neben Meter, Kilogramm und Sekunde (MKS) sind dies das Ampere, das Kelvin – bis 1968 noch als „Grad Kelvin“ bezeichnet – sowie die Candela.[25]

1960: Auf der 11. CGPM erhält dieses erweiterte MKS-System die französische Bezeichnung Système International d’Unités (SI) („Internationales Einheitensystem“).[26] Der Meter wird über die Wellenlänge von Licht neu definiert.[27]

1967: Auf der 13. CGPM erhält die Sekunde ihre heute gültige, atomphysikalische Definition.[28]

1971: Auf der 14. CGPM kommt als siebte und letzte Basiseinheit das Mol hinzu und wird an die 6. Stelle zwischen Kelvin und Candela eingeordnet.[29]

1979: Auf der 16. CGPM erhält die Candela ihre heute gültige Definition und wird dabei mit dem Watt verknüpft.[30] Dadurch werden die photometrischen Einheiten an das MKS-System angebunden.

1983: Die 17. CGPM definiert den Meter neu, indem der Lichtgeschwindigkeit ein fester Wert zugewiesen wird.[31]

2018: Die 26. CGPM beschließt mit Wirkung zum 20. Mai 2019 eine grundlegende Reform: Alle Basiseinheiten und damit alle Einheiten überhaupt werden nun auf sieben physikalische Konstanten zurückgeführt, denen feste Werte zugewiesen werden.[10] Mit Ausnahme der Sekunde[A 4] werden die Einheiten damit von der Realisierung und deren begrenzter Genauigkeit unabhängig („Definitionen für die Ewigkeit“).

Siehe auch

Zur Verwendung mit dem SI zugelassene Einheiten

Literatur

Eugen Bodea: Giorgis rationales MKS-Masssystem mit Dimensionskohärenz. 2. Auflage. Birkhäuser, 1949.
Das System der Einheiten. In: PTB-Mitteilungen 122 (2012) Heft 1, S. 1-102. (online) (PDF; 5,8 MB)

Weblinks

Commons: Internationales Einheitensystem – Sammlung von Bildern, Videos und Audiodateien

Das Internationale Einheitensystem, Internationales Büro für Maß und Gewicht (BIPM) (englisch, französisch)
Le Système international d’unités, 9e édition, 2019, die sogenannte „SI-Broschüre“, BIPM (englisch, französisch)

Anmerkungen

Bei c, h und e handelt es sich um fundamentale Naturkonstanten. Δν_Cs ist eine universell reproduzierbare Frequenz, die unabhängig von einer Realisierungsvorschrift ist. N_A ist ein durch Übereinkunft festgelegter Zahlenwert, der möglichst genau dem Umrechnungsfaktor zwischen der atomaren Masseneinheit und der SI-Einheit „Gramm“ entsprechen soll. k_B und K_cd sind (ebenfalls willkürlich festgelegte) Umrechnungsfaktoren zwischen den thermodynamischen bzw. photometrischen Einheiten und den MKS-Einheiten (siehe SI-Broschüre, 9. Aufl., Kap. 2.2.1).
Bisweilen wird gesagt, das SI gelte nicht in den USA. Dies trifft nicht zu: Seit dem Metric Act von 1866, erweitert 2007 auf das SI, ist das metrische System in den USA zugelassen. Seit dem Metric Conversion Act von 1975 ist es das preferred measurement system for U.S. trade and commerce, allerdings nicht verpflichtend. Für den Handel mit Endverbrauchern schreibt der Fair Packaging and Labeling Act seit 1994 die Kennzeichnung sowohl in metrischen Einheiten als auch in customary units vor.
Für abgeleitete Einheiten, die durch Division entstehen, ist im Deutschen das Wort „durch“ normgerecht – z. B. „Meter durch Sekunde“ (m/s). Umgangssprachlich ist aber das Wort „pro“ üblich.
Die Größe Δν_Cs ist die Frequenz der Strahlung, die beim Übergang zwischen zwei speziellen Energieniveaus des Caesium-133-Atoms emittiert wird. Dies ist keine Materialeigenschaft, sondern ein nicht beeinflussbarer atomarer Vorgang. Allerdings ist damit die Realisierung der Sekunde an diesen Vorgang gebunden. Mittlerweile wurden Atomuhren entwickelt, die auf anderen Atomen beruhen und noch größere Präzision ermöglichen. Es kann sein, dass man deshalb die Sekunde neu definieren wird.
Die Einheiten „Kelvin“ und „Candela“ sind nicht von der Lichtgeschwindigkeit c abhängig. Zwar hängt ihre Definition in der hier gezeigten Darstellung u. a. von den Einheiten „Meter“ und „Kilogramm“ ab und diese wiederum von c. Führt man Kelvin und Candela jedoch ganz auf die definierenden Konstanten des SI zurück, kürzt sich bei der Rechnung c heraus.
Es gibt abgeleitete Einheiten, die „direkter“, d. h. durch weniger Konstanten definiert sind als Basiseinheiten: Das Coulomb ist allein durch die Konstante e definiert, für das Ampere benötigt man zusätzlich Δν_Cs. Für Joule und Watt sind nur h und Δν_Cs erforderlich, für das Kilogramm zusätzlich c.
Für Vielfache des kg ist auch die Verwendung der Nicht-SI-Einheit Tonne (1 t = 10³ kg = 1 Mg) zulässig und üblich, aus der wiederum mit Präfixen Einheiten wie „Kilotonne“ (kt) oder „Megatonne“ (Mt) gebildet werden können.

Einzelnachweise

Text der Einheitenverordnung
DIN EN ISO 80000-3:2013 Größen und Einheiten – Teil 3: Raum und Zeit, Abschnitt 3-8.b
Le Système international d’unités. 9e édition, 2019 (die sogenannte „SI-Broschüre“, französisch und englisch).
Das Internationale Einheitensystem (SI). Deutsche Übersetzung der BIPM-Broschüre „Le Système international d’unités/The International System of Units (8e édition, 2006)“. In: PTB-Mitteilungen. Band 117, Nr. 2, 2007 (Online [PDF; 1,4 MB]). – Zu beachten: Dies ist die Übersetzung der SI-Broschüre von 2006; die Übersetzung der aktuellen Version liegt noch nicht vor.
Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen
Richtlinie (EU) 2019/1258 der Kommission vom 23. Juli 2019 zur Änderung des Anhangs der Richtlinie 80/181/EWG des Rates hinsichtlich der Definitionen der SI-Basiseinheiten zwecks ihrer Anpassung an den technischen Fortschritt, enthält Übersetzungen der Definitionen aus der SI-Broschüre, 9. Aufl.
CIPM: Report of the 90th meeting (2001). In: bipm.org. Bureau International des Poids et Mesures, abgerufen am 1. April 2021 (englisch). S. 120, Kap. 6.1.2
SI-Broschüre, 9. Aufl., Anhang 1, S. 72 (frz.) und S. 180 (engl.)
SI-Broschüre, 9. Aufl., Kap. 2.3.1, S. 21 (frz.) und S. 133 (engl.)
Resolution 1 of the 26th CGPM. On the revision of the International System of Units (SI). Bureau International des Poids et Mesures, 2018, abgerufen am 12. April 2021 (englisch).
Das neue Internationale Einheitensystem (SI) (PDF; 665 kB) Broschüre der PTB mit Erklärung und Beschreibung der Neudefinition der Basiseinheiten 2019, abgerufen am 14. März 2021
“Prior to the definitions adopted in 2018, the SI was defined through seven base units from which the derived units were constructed as products of powers of the base units. Defining the SI by fixing the numerical values of seven defining constants has the effect that this distinction is, in principle, not needed […] Nevertheless, the concept of base and derived units is maintained because it is useful and historically well established […]”, SI-Broschüre, Kapitel 2.3 bipm.org (PDF)
Neue Definitionen im Internationalen Einheitensystem (SI). (PDF; 1,3 MB) PTB, abgerufen am 31. Oktober 2019.
Resolution 10 of the 22nd CGPM. Symbol for the decimal marker. Bureau International des Poids et Mesures, 2003, abgerufen am 12. April 2021 (englisch).
DIN EN ISO 80000-1:2013-08, Größen und Einheiten – Teil 1: Allgemeines; Deutsche Fassung von EN ISO 80000-1:2013.
Grandes Lois de la République, abgerufen am 18. September 2020 (französisch)
J. C. Maxwell: A Treatise on Electricity and Magnetism. Clarendon Press, Oxford 1873, Vol. 1 S. 3–4; Wikisource
Resolution 1 of the 1st CGPM. Sanction of the international prototypes of the metre and the kilogram. Bureau International des Poids et Mesures, 1889, abgerufen am 12. April 2021 (englisch).
„Dem gegenüber dürfte es nicht ohne Interesse sein zu bemerken, dass mit Zuhülfenahme der beiden […] Constanten a und b die Möglichkeit gegeben ist, Einheiten für Länge, Masse, Zeit und Temperatur aufzustellen, welche, unabhängig von speciellen Körpern und Substanzen, ihre Bedeutung für alle Zeiten und für alle, auch ausserirdische und aussermenschliche Culturen notwendig behalten und welche daher als ‚natürliche Maaßeinheiten‘ bezeichnet werden können.“ – M. Planck. In: Ann. Physik, 1, 1900, S. 69; nach: Naturkonstanten als Hauptdarsteller
J. de Boer: Giorgi and the International System of Units. In: C. Egidi (Hrsg.): Giovanni Giorgi and his contribution to electrical metrology. Politecnico, Torino 1990, S. 33–39.
Arthur E. Kennelly: Adoption of the Meter-Kilogram-Mass-Second (M.K.S.) Absolute System of Practical Units by the International Electrotechnical Commission (I.E.C.), Bruxelles, June, 1935 (PDF; 451 kB)
Historical perspective: Unit of electric current, ampere. In: bipm.org. Bureau International des Poids et Mesures, abgerufen am 22. November 2021 (englisch).
Resolution 6 of the 9th CGPM. Proposal for establishing a practical system of units of measurement. Bureau International des Poids et Mesures, 1948, abgerufen am 12. April 2021 (englisch).
Resolution 7 of the 9th CGPM (1948). Writing and printing of unit symbols and of numbers. Bureau International des Poids et Mesures, 1948, abgerufen am 21. Februar 2022 (englisch).
Resolution 6 of the 10th CGPM. Practical system of units. Bureau International des Poids et Mesures, 1954, abgerufen am 12. April 2021 (englisch).
Resolution 12 of the 11th CGPM. Système International d'Unités. Bureau International des Poids et Mesures, 1960, abgerufen am 12. April 2021 (englisch).
Resolution 6 of the 11th CGPM. Definition of the metre. Bureau International des Poids et Mesures, 1960, abgerufen am 12. April 2021 (englisch).
Resolution 1 of the 13th CGPM. SI unit of time (second). Bureau International des Poids et Mesures, 1967, abgerufen am 9. August 2021 (englisch).
Resolution 3 of the 14th CGPM. SI unit of amount of substance (mole). Bureau International des Poids et Mesures, 1971, abgerufen am 12. April 2021 (englisch).
Resolution 3 of the 16th CGPM. SI unit of luminous intensity (candela). Bureau International des Poids et Mesures, 1979, abgerufen am 12. April 2021 (englisch).
Resolution 1 of the 17th CGPM. Definition of the metre. Bureau International des Poids et Mesures, 1983, abgerufen am 12. April 2021 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[anm7konst-1] Bei c, h und e handelt es sich um fundamentale Naturkonstanten. Δν_Cs ist eine universell reproduzierbare Frequenz, die unabhängig von einer Realisierungsvorschrift ist. N_A ist ein durch Übereinkunft festgelegter Zahlenwert, der möglichst genau dem Umrechnungsfaktor zwischen der atomaren Masseneinheit und der SI-Einheit „Gramm“ entsprechen soll. k_B und K_cd sind (ebenfalls willkürlich festgelegte) Umrechnungsfaktoren zwischen den thermodynamischen bzw. photometrischen Einheiten und den MKS-Einheiten (siehe SI-Broschüre, 9. Aufl., Kap. 2.2.1).

[usa-2] Bisweilen wird gesagt, das SI gelte nicht in den USA. Dies trifft nicht zu: Seit dem Metric Act von 1866, erweitert 2007 auf das SI, ist das metrische System in den USA zugelassen. Seit dem Metric Conversion Act von 1975 ist es das preferred measurement system for U.S. trade and commerce, allerdings nicht verpflichtend. Für den Handel mit Endverbrauchern schreibt der Fair Packaging and Labeling Act seit 1994 die Kennzeichnung sowohl in metrischen Einheiten als auch in customary units vor.

[durch-11] Für abgeleitete Einheiten, die durch Division entstehen, ist im Deutschen das Wort „durch“ normgerecht – z. B. „Meter durch Sekunde“ (m/s). Umgangssprachlich ist aber das Wort „pro“ üblich.

[sekunde-14] Die Größe Δν_Cs ist die Frequenz der Strahlung, die beim Übergang zwischen zwei speziellen Energieniveaus des Caesium-133-Atoms emittiert wird. Dies ist keine Materialeigenschaft, sondern ein nicht beeinflussbarer atomarer Vorgang. Allerdings ist damit die Realisierung der Sekunde an diesen Vorgang gebunden. Mittlerweile wurden Atomuhren entwickelt, die auf anderen Atomen beruhen und noch größere Präzision ermöglichen. Es kann sein, dass man deshalb die Sekunde neu definieren wird.

[kelvindef-15] Die Einheiten „Kelvin“ und „Candela“ sind nicht von der Lichtgeschwindigkeit c abhängig. Zwar hängt ihre Definition in der hier gezeigten Darstellung u. a. von den Einheiten „Meter“ und „Kilogramm“ ab und diese wiederum von c. Führt man Kelvin und Candela jedoch ganz auf die definierenden Konstanten des SI zurück, kürzt sich bei der Rechnung c heraus.

[direkt-17] Es gibt abgeleitete Einheiten, die „direkter“, d. h. durch weniger Konstanten definiert sind als Basiseinheiten: Das Coulomb ist allein durch die Konstante e definiert, für das Ampere benötigt man zusätzlich Δν_Cs. Für Joule und Watt sind nur h und Δν_Cs erforderlich, für das Kilogramm zusätzlich c.

[kilotonne-22] Für Vielfache des kg ist auch die Verwendung der Nicht-SI-Einheit Tonne (1 t = 10³ kg = 1 Mg) zulässig und üblich, aus der wiederum mit Präfixen Einheiten wie „Kilotonne“ (kt) oder „Megatonne“ (Mt) gebildet werden können.

[EHV-3] Text der Einheitenverordnung

[din-iso-80000-4] DIN EN ISO 80000-3:2013 Größen und Einheiten – Teil 3: Raum und Zeit, Abschnitt 3-8.b

[SI-Brosch-5] Le Système international d’unités. 9e édition, 2019 (die sogenannte „SI-Broschüre“, französisch und englisch).

[SI-Brosch-de-6] Das Internationale Einheitensystem (SI). Deutsche Übersetzung der BIPM-Broschüre „Le Système international d’unités/The International System of Units (8e édition, 2006)“. In: PTB-Mitteilungen. Band 117, Nr. 2, 2007 (Online [PDF; 1,4 MB]). – Zu beachten: Dies ist die Übersetzung der SI-Broschüre von 2006; die Übersetzung der aktuellen Version liegt noch nicht vor.

[7] Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen

[EU-2019-8] Richtlinie (EU) 2019/1258 der Kommission vom 23. Juli 2019 zur Änderung des Anhangs der Richtlinie 80/181/EWG des Rates hinsichtlich der Definitionen der SI-Basiseinheiten zwecks ihrer Anpassung an den technischen Fortschritt, enthält Übersetzungen der Definitionen aus der SI-Broschüre, 9. Aufl.

[CIPM2001-9] CIPM: Report of the 90th meeting (2001). In: bipm.org. Bureau International des Poids et Mesures, abgerufen am 1. April 2021 (englisch). S. 120, Kap. 6.1.2

[SI-Einh-10] SI-Broschüre, 9. Aufl., Anhang 1, S. 72 (frz.) und S. 180 (engl.)

[Celsius-12] SI-Broschüre, 9. Aufl., Kap. 2.3.1, S. 21 (frz.) und S. 133 (engl.)

[CGPM-26-1-13] Resolution 1 of the 26th CGPM. On the revision of the International System of Units (SI). Bureau International des Poids et Mesures, 2018, abgerufen am 12. April 2021 (englisch).

[PTB1711-16] Das neue Internationale Einheitensystem (SI) (PDF; 665 kB) Broschüre der PTB mit Erklärung und Beschreibung der Neudefinition der Basiseinheiten 2019, abgerufen am 14. März 2021

[SI9-2-3-18] “Prior to the definitions adopted in 2018, the SI was defined through seven base units from which the derived units were constructed as products of powers of the base units. Defining the SI by fixing the numerical values of seven defining constants has the effect that this distinction is, in principle, not needed […] Nevertheless, the concept of base and derived units is maintained because it is useful and historically well established […]”, SI-Broschüre, Kapitel 2.3 bipm.org (PDF)

[def-allebasis-PTB-19] Neue Definitionen im Internationalen Einheitensystem (SI). (PDF; 1,3 MB) PTB, abgerufen am 31. Oktober 2019.

[CGPM-22-10-20] Resolution 10 of the 22nd CGPM. Symbol for the decimal marker. Bureau International des Poids et Mesures, 2003, abgerufen am 12. April 2021 (englisch).

[EN80000-1-21] DIN EN ISO 80000-1:2013-08, Größen und Einheiten – Teil 1: Allgemeines; Deutsche Fassung von EN ISO 80000-1:2013.

[gesetz1793-23] Grandes Lois de la République, abgerufen am 18. September 2020 (französisch)

[maxwell-24] J. C. Maxwell: A Treatise on Electricity and Magnetism. Clarendon Press, Oxford 1873, Vol. 1 S. 3–4; Wikisource

[CGPM-1-1-25] Resolution 1 of the 1st CGPM. Sanction of the international prototypes of the metre and the kilogram. Bureau International des Poids et Mesures, 1889, abgerufen am 12. April 2021 (englisch).

[planck-26] „Dem gegenüber dürfte es nicht ohne Interesse sein zu bemerken, dass mit Zuhülfenahme der beiden […] Constanten a und b die Möglichkeit gegeben ist, Einheiten für Länge, Masse, Zeit und Temperatur aufzustellen, welche, unabhängig von speciellen Körpern und Substanzen, ihre Bedeutung für alle Zeiten und für alle, auch ausserirdische und aussermenschliche Culturen notwendig behalten und welche daher als ‚natürliche Maaßeinheiten‘ bezeichnet werden können.“ – M. Planck. In: Ann. Physik, 1, 1900, S. 69; nach: Naturkonstanten als Hauptdarsteller

[giorgi-27] J. de Boer: Giorgi and the International System of Units. In: C. Egidi (Hrsg.): Giovanni Giorgi and his contribution to electrical metrology. Politecnico, Torino 1990, S. 33–39.

[IEC35-28] Arthur E. Kennelly: Adoption of the Meter-Kilogram-Mass-Second (M.K.S.) Absolute System of Practical Units by the International Electrotechnical Commission (I.E.C.), Bruxelles, June, 1935 (PDF; 451 kB)

[SI-history-ampere-29] Historical perspective: Unit of electric current, ampere. In: bipm.org. Bureau International des Poids et Mesures, abgerufen am 22. November 2021 (englisch).

[CGPM-9-6-30] Resolution 6 of the 9th CGPM. Proposal for establishing a practical system of units of measurement. Bureau International des Poids et Mesures, 1948, abgerufen am 12. April 2021 (englisch).

[CGPM-9-7-31] Resolution 7 of the 9th CGPM (1948). Writing and printing of unit symbols and of numbers. Bureau International des Poids et Mesures, 1948, abgerufen am 21. Februar 2022 (englisch).

[CGPM-10-6-32] Resolution 6 of the 10th CGPM. Practical system of units. Bureau International des Poids et Mesures, 1954, abgerufen am 12. April 2021 (englisch).

[CGPM-11-12-33] Resolution 12 of the 11th CGPM. Système International d'Unités. Bureau International des Poids et Mesures, 1960, abgerufen am 12. April 2021 (englisch).

[CGPM-11-6-34] Resolution 6 of the 11th CGPM. Definition of the metre. Bureau International des Poids et Mesures, 1960, abgerufen am 12. April 2021 (englisch).

[CGPM-13-1-35] Resolution 1 of the 13th CGPM. SI unit of time (second). Bureau International des Poids et Mesures, 1967, abgerufen am 9. August 2021 (englisch).

[CGPM-14-3-36] Resolution 3 of the 14th CGPM. SI unit of amount of substance (mole). Bureau International des Poids et Mesures, 1971, abgerufen am 12. April 2021 (englisch).

[CGPM-16-3-37] Resolution 3 of the 16th CGPM. SI unit of luminous intensity (candela). Bureau International des Poids et Mesures, 1979, abgerufen am 12. April 2021 (englisch).

[CGPM-17-1-38] Resolution 1 of the 17th CGPM. Definition of the metre. Bureau International des Poids et Mesures, 1983, abgerufen am 12. April 2021 (englisch).