Gibbs-Energie

Die Gibbs-Energie (auch freie Enthalpie), benannt nach Josiah Willard Gibbs, ist ein thermodynamisches Potential, also eine Zustandsgröße in der Thermodynamik.[1] Sie ist eine extensive Größe mit der Dimension Energie. Im SI-Einheitensystem wird sie in der Einheit Joule gemessen. Ihr Formelzeichen ist $G$ und ihre natürlichen Variablen sind die Temperatur, der Druck $p$ und die Teilchenzahlen $\{N_{i}\}$ .

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Physikalische Größe

Name

Freie Enthalpie,
Gibbs-Energie

Größenart

Energie

Formelzeichen

$G$

Größen- und Einheitensystem	Einheit	Dimension
SI	J = kg·m²·s⁻²	L²·M·T⁻²

Die Gibbs-Energie eines Systems ergibt sich aus dessen Enthalpie $H$ durch eine Legendre-Transformation bezüglich der Entropie, indem die Enthalpie um das Produkt aus der absoluten Temperatur $T$ und der Entropie $S$ verringert wird:[2]

G(T,p,\{N_{i}\})=H(S,p,\{N_{i}\})-T\,S

.

oder von der inneren Energie $U$ ausgehend:

G(T,p,\{N_{i}\})=U(S,V,\{N_{i}\})+p\,V-T\,S

.

wobei $V$ das Volumen des Systems ist.

Die molare Gibbs-Energie (Einheit: J/mol) ist die auf die Stoffmenge $n$ bezogene Gibbs-Energie:

G_{\text{m}}={\frac {G}{n}}

.

Die spezifische Gibbs-Energie (Einheit: J/kg) ist die auf die Masse $m$ bezogene Gibbs-Energie:

g={\frac {G}{m}}

.

Die molare und die spezifische Gibbs-Energie sind intensive Größen: Haben zwei identische Teilsysteme die gleiche molare oder spezifische Gibbs-Energie, dann hat auch das aus ihnen gebildete Gesamtsystem diese molare bzw. spezifische Gibbs-Energie.

Überblick

Die Gibbs-Energie wird in Joule gemessen, sie ist aber keine eigenständige Energieform, wie beispielsweise die kinetische Energie oder die im System enthaltene innere Energie oder eine umgesetzte Reaktionswärme. Sie darf bei der Berechnung der Gesamtenergie nicht mitsummiert werden. Sie ist lediglich eine Abkürzung für den häufig auftretenden Ausdruck $U+p\,V-T\,S$ . Mit ihrer Hilfe lassen sich Aussagen über das Verhalten des Systems machen, wie beispielsweise über die Richtung freiwillig ablaufender Prozesse oder die Lage von Gleichgewichtszuständen.

Gibbs-Energie als Gleichgewichtskriterium

Ein Prozess in einem gegebenen thermodynamischen System läuft genau dann freiwillig ab, wenn er mit einer Zunahme der Gesamtentropie des Systems und seiner Umgebung verbunden ist. Beschränkt man sich auf Prozesse, die bei konstant gehaltener Temperatur und konstant gehaltenem Druck ablaufen, dann sind die Prozesse, welche die Entropie von System und Umgebung erhöhen, genau diejenigen, welche die Gibbs-Energie des Systems verringern. Ein auf konstanter Temperatur und unter konstantem Druck gehaltenes geschlossenes System nimmt daher jenen Zustand als Gleichgewichtszustand an, in dem seine Gibbs-Energie den kleinsten möglichen Wert besitzt. Befindet sich das System nicht im Gleichgewicht, geht es freiwillig (sofern keine anderweitigen Hemmungen vorliegen) in Zustände geringerer Gibbs-Energie über, bis das Gleichgewicht erreicht ist. Da zahlreiche physikalische und chemische Prozesse bei konstanter Temperatur (isotherm) und konstantem Druck (isobar) ablaufen, liefert die Gibbs-Energie ein häufig anwendbares Kriterium für die Richtung, in welcher der Prozess freiwillig abläuft und für die Lage des Gleichgewichts.

So gilt beispielsweise für eine isotherme und isobare chemische Reaktion:

Ist die Gibbs-Energie der Reaktionsprodukte kleiner als die Gibbs-Energie der Ausgangsstoffe ( $\Delta G<0$ ), dann läuft die Reaktion in Richtung der Produkte ab.
Ist die Gibbs-Energie der Reaktionsprodukte größer als die Gibbs-Energie der Ausgangsstoffe ( $\Delta G>0$ ), dann läuft die Reaktion in umgekehrter Richtung ab.
Die Gibbs-Energie des Gemischs aus Ausgangsstoffen und Produkten hängt in der Regel von der Mischung ab und ändert sich daher im Verlaufe einer Reaktion. Durchläuft sie dabei ein Minimum, ist also bei Erreichen einer bestimmten Mischung ( $\mathrm {d} G=0$ ), dann laufen in diesem Zustand die Hin- und die Rückreaktion mit gleicher Geschwindigkeit ab, das reagierende System hat ein chemisches Gleichgewicht erreicht.

Zwei Phasen einer Substanz stehen genau dann im Gleichgewicht miteinander, wenn die molaren (oder die spezifischen) Gibbs-Energien der Substanz in beiden Phasen gleich sind. Sind die molaren Gibbs-Energien der beteiligten Phasen bekannt, lässt sich also sofort erkennen, ob Gleichgewicht vorliegt oder nicht. Umgekehrt ist bei Vorliegen eines Gleichgewichts die molare Gibbs-Energie aller Phasen bekannt, sobald sie für eine Phase bekannt ist. Liegt beispielsweise flüssiges Wasser im Gleichgewicht mit seinem Dampf vor, dann haben die beiden Phasen dieselbe molare Gibbs-Energie. Diejenige des Dampfes lässt sich (näherungsweise als ideales Gas betrachtet) leicht berechnen, der gefundene Zahlenwert gilt auch für das flüssige Wasser.
Bestehen die Phasen aus Mischungen mehrerer Substanzen, gilt das Gleichgewichtskriterium für jede in der Mischung enthaltene Substanz separat.

Chemisches Potential

In einem Einkomponentensystem ist das chemische Potential identisch mit der molaren Gibbs-Energie des Systems. In einem Mehrkomponentensystem sind die chemischen Potentiale identisch mit den partiellen molaren Gibbs-Energien des Systems.

Änderung der Gibbs-Energie eines Systems

Ändert man die Temperatur eines Systems bei konstantem Druck und konstanten Stoffmengen, ändert sich die Gibbs-Energie des Systems proportional zur Temperaturänderung, die Proportionalitätskonstante ist das Negative der Entropie des Systems; ändert man unter gleichen Bedingungen den Druck, so ändert sich die Gibbs-Energie proportional zur Druckänderung (Proportionalitätskonstante: Volumen des Systems).

Ändert man die Stoffmenge einer der im System enthaltenen Substanzen bei konstanter Temperatur, konstantem Druck und konstanten Stoffmengen der übrigen Substanzen, ändert sich die Gibbs-Energie des Systems proportional zur Stoffmengenänderung, die Proportionalitätskonstante ist das chemische Potential der betreffenden Substanz unter den im System herrschenden Bedingungen.

Wird an einem auf konstanter Temperatur und unter konstantem Druck gehaltenen geschlossenen System ein bestimmter Betrag reversibler physikalischer Arbeit (außer Volumenänderungsarbeit $p\,\mathrm {d} V$ ) geleistet, nimmt die Gibbs-Energie des Systems um den betreffenden Betrag zu. So lässt sich die Gibbs-Energie eines Systems gezielt erhöhen, indem beispielsweise ein bekannter Betrag an Hubarbeit oder elektrischer Arbeit am System geleistet wird. Leistet umgekehrt das System unter den genannten Bedingungen Arbeit (außer Volumenänderungsarbeit), nimmt seine Gibbs-Energie um den betreffenden Betrag ab.

Die Gleichheit der Beträge von umgesetzter Arbeit und Änderung der Gibbs-Energie gilt nur im Fall reversibel geleisteter Arbeit. Im irreversiblen Fall ist je nach dem Ausmaß der Irreversibilität die am System zu leistende Arbeit größer beziehungsweise die vom System geleistete Arbeit geringer als die Änderung der Gibbs-Energie.
In diesem Zusammenhang liefert die Gibbs-Energie ein Maß für die „Triebkraft“ des Prozesses, wie beispielsweise die „Affinität“ der Reaktanden in einer chemischen Reaktion.

Als Fundamentalgleichung

Aus der Gibbs-Energie lässt sich die gesamte thermodynamische Information über das System ableiten. Voraussetzung ist jedoch, dass sie als Funktion der Variablen Temperatur $T$ , Druck $p$ und Molzahlen $n_{i}$ der im System enthaltenen chemischen Komponenten gegeben ist. Dies sind die „natürlichen Variablen“ der Gibbs-Energie. Sie lässt sich auch als Funktion anderer Variablen ansetzen, enthält dann aber nicht mehr die vollständige thermodynamische Information.

Minimumsprinzip der Gibbs-Energie

Gemäß dem Zweiten Hauptsatz der Thermodynamik nimmt ein abgeschlossenes System unter den erreichbaren Zuständen denjenigen als Gleichgewichtszustand ein, der bei der gegebenen inneren Energie die höchste Entropie besitzt. Aus diesem Maximumsprinzip der Entropie lassen sich auch andere, gleichbedeutende Extremalprinzipien ableiten, wie beispielsweise ein Minimumsprinzip der inneren Energie:[3]^:132ff. Bei konstant gehaltener Entropie nimmt ein System denjenigen Zustand als Gleichgewichtszustand ein, der die geringste innere Energie besitzt.

Ein ähnliches Minimumsprinzip existiert für die Gibbs-Energie: Ein System, dessen Temperatur und Druck konstant gehalten werden und das keine Arbeit leistet außer Volumenänderungsarbeit,[4] nimmt von allen erreichbaren Zuständen mit dieser Temperatur und diesem Druck denjenigen als Gleichgewichtszustand ein, in dem die Gibbs-Energie den kleinstmöglichen Wert hat.[3]^:157

Zum Beweis betrachte man ein geschlossenes[Anm. 1] System, dessen Temperatur und Druck auf einem jeweils konstanten Wert gehalten werden. Die Temperatur kann konstant gehalten werden, indem das betrachtete System über eine wärmedurchlässige Wand in Kontakt mit einem zweiten System steht, das unveränderlich die gewünschte Temperatur aufweist (in thermodynamischer Ausdrucksweise: ein Wärmereservoir). Über einen Wärmestrom durch die Kontaktwand kann das betrachtete System im Falle eines Temperaturunterschieds so lange Wärme mit dem Wärmereservoir austauschen, bis es seine Temperatur wieder derjenigen des Reservoirs angeglichen hat. Der Druck kann konstant gehalten werden, indem das System über eine wärmeundurchlässige aber flexible Wand mit einem System in Kontakt steht, das unveränderlich den gewünschten Druck aufweist (ein Volumenreservoir). Durch Verformung der flexiblen Wand kann das betrachtete System im Falle eines Druckunterschieds so lange mit dem Volumenreservoir „Volumen austauschen“, bis es seinen Druck wieder dem des Volumenreservoirs angeglichen hat.

Im Verlaufe eines beliebigen Prozesses ändern sich in der Regel die Entropien des Systems und des Wärmereservoirs (das Volumenreservoir tauscht mit dem betrachteten System keine Wärme und keine Materie, also auch keine Entropie aus). Gemäß dem Zweiten Hauptsatz der Thermodynamik nimmt die Entropie des aus betrachtetem System und Wärmereservoir gebildeten abgeschlossenen Gesamtsystems zu oder bleibt bestenfalls gleich:

\mathrm {d} (S_{\mathrm {Sys} }+S_{\mathrm {Res} })=\mathrm {d} S_{\mathrm {Sys} }+\mathrm {d} S_{\mathrm {Res} }\geq 0

,

oder

\mathrm {d} S_{\mathrm {Sys} }\geq -\mathrm {d} S_{\mathrm {Res} }

.

Das „größer“-Zeichen gilt für Prozesse, welche die Entropie des Gesamtsystems vermehren und daher freiwillig aus eigenem Antrieb ablaufen. Diese Prozesse laufen von selbst (sofern keine anderweitige Hemmung vorliegt) in Richtung des Gleichgewichtszustands ab. Das Gleichheitszeichen gilt, wenn das Gesamtsystem die größte unter den gegebenen Bedingungen erreichbare Entropie angenommen und damit den thermischen Gleichgewichtszustand erreicht hat.

Die Entropieänderung $\mathrm {d} S_{\mathrm {Res} }$ des Reservoirs steht mit der in das Reservoir fließenden Wärme $\mathrm {d} Q_{\mathrm {Res} }$ und der Temperatur des Reservoirs $T_{\mathrm {Res} }$ definitionsgemäß in der Beziehung

\mathrm {d} S_{\mathrm {Res} }=\mathrm {d} Q_{\mathrm {Res} }/T_{\mathrm {Res} }

.

Weil das Reservoir und das betrachtete System die Wärme ausschließlich untereinander austauschen, ist $\mathrm {d} Q_{\mathrm {Sys} }=-\mathrm {d} Q_{\mathrm {Res} }$ , und da das System und das Reservoir laut Voraussetzung dieselbe Temperatur aufweisen, ist $T_{\mathrm {Sys} }=T_{\mathrm {Res} }$ . Daher folgt aus obiger Ungleichung

\mathrm {d} S_{\mathrm {Sys} }\geq \mathrm {d} Q_{\mathrm {Sys} }/T_{\mathrm {Sys} }

.

Damit ist es gelungen, das Entropiekriterium, das die Entropien von System und Reservoir betrachtet, ausschließlich unter Verwendung von Größen des betrachteten Systems zu formulieren, was die Anwendung stark erleichtert. Da keine Unterscheidung mehr nötig ist, werden die Indizes an den Größen des Systems nun fortgelassen und die Ungleichung lautet

\mathrm {d} S\geq \mathrm {d} Q/T

(Clausiussche Ungleichung).[5]

Ferner sei nun vorausgesetzt, dass das System unter konstantem Druck gehalten wird (isobarer Prozess, $\mathrm {d} p=0$ ) und dass das System außerdem so beschaffen sei, dass es außer Volumenänderungsarbeit keine anderen Arten von Arbeit leisten kann. Dann ist die zu- oder abgeführte Wärmemenge zahlenmäßig gleich der Enthalpieänderung des Systems ( $\mathrm {d} H=\mathrm {d} Q$ , siehe → Enthalpie), und aus der Clausiusschen Ungleichung folgt

\mathrm {d} S\geq \mathrm {d} H/T

oder umgestellt

\mathrm {d} H-T\,\mathrm {d} S\leq 0\quad (*)

.

Andererseits ist die Änderung der Gibbs-Energie des Systems gemäß ihrer Definition

\mathrm {d} G=\mathrm {d} (H-T\,S)=\mathrm {d} U+p\mathrm {d} V+V\mathrm {d} p-T\mathrm {d} S-S\mathrm {d} T

,

was sich im vorliegenden Fall wegen der vorausgesetzten Konstanz der Temperatur ( $\mathrm {d} T=0$ ) und des Drucks ( $\mathrm {d} p=0$ ) zu

\mathrm {d} G=\mathrm {d} H-T\,\mathrm {d} S\quad (*)

vereinfacht. Vergleich der markierten Gleichungen $(*)$ liefert schließlich die Aussage:[4]

\mathrm {d} G\leq 0

.

Das „kleiner“-Zeichen gilt für Prozesse, die freiwillig ablaufen. Das Gleichheitszeichen gilt, sobald das System den Gleichgewichtszustand erreicht hat.

Das Maximumsprinzip für die Entropie des Gesamtsystems führt also dazu, dass die Gibbs-Energie des betrachteten Systems auf der Untermenge der Zustände mit konstanter Temperatur und konstantem Druck ein Minimum annimmt. Ist das System noch nicht im Gleichgewicht, bewegt es sich (falls isotherme und isobare Bedingungen vorliegen und das System keine Nicht-Volumenarbeit leistet) freiwillig in Zustände niedrigerer Gibbs-Energie. Das Gleichgewicht ist mit dem Zustand erreicht, in dem die Gibbs-Energie den unter den gegebenen Bedingungen kleinstmöglichen Wert besitzt.

Wollte man den Gleichgewichtszustand mit Hilfe des (allgemein und stets gültigen) Entropiekriteriums direkt bestimmen, müsste das Maximum der Gesamtentropie ermittelt werden, also die Summe der Entropien des untersuchten Systems und seiner Umgebung. Es müsste daher nicht nur die Änderung der System-Entropie bei einer Zustandsänderung betrachtet werden, sondern auch die Entropie-Änderung, die das System durch Rückwirkung auf die Umgebung dort erzeugt. Das Gibbs-Energie-Kriterium ist eine Umformulierung des Entropiekriteriums, in welche ausschließlich Eigenschaften des betrachteten Systems eingehen und welche die Rückwirkung auf die Umgebung (unter isothermen und isobaren Bedingungen) durch den Term $-T\,S$ automatisch berücksichtigt, denn unter den gegebenen Bedingungen ist $\mathrm {d} (-T\,S)=\mathrm {d} (T_{\mathrm {Res} }S_{\mathrm {Res} })$ .[3]^:156 Bei Verwendung des Gibbs-Energie-Kriteriums kann die Ermittlung des (isothermen und isobaren) Gleichgewichtszustands sich also auf die Betrachtung des Systems beschränken, was die Untersuchungen merklich erleichtert.[6]

Für einen realen physikalischen oder chemischen Prozess kann oft die Atmosphäre als Wärme- und Volumenreservoir dienen. Wegen ihres großen Volumens ändern sich ihre Temperatur und ihr Druck nicht nennenswert, wenn ein System Wärme oder Volumen auf sie überträgt. Die Voraussetzungen für die Anwendbarkeit des Minimumsprinzips der Gibbs-Energie sind also insbesondere erfüllt, wenn ein System der freien Atmosphäre ausgesetzt ist und seine Prozesse daher isotherm und isobar ablaufen. Sie sind aber beispielsweise auch erfüllt, wenn ein Teilsystem innerhalb eines größeren Systems betrachtet wird, welches aufgrund seiner Größe ein Wärme- und Volumenreservoir für das Teilsystem (etwa für eine Traube in einem Gärbottich[3]^:167) darstellt.

Man vergleiche das Minimumsprinzip der Gibbs-Energie unter isothermen und isobaren Bedingungen mit den Extremalprinzipien anderer thermodynamischer Potentiale, welche die Gleichgewichtsbedingungen in geschlossenen Systemen unter anderen Randbedingungen darstellen:[7]^:50

Konstant gehaltene Größen	Gleichgewichtsbedingung
Innere Energie $U$ und Volumen $V$	Maximum der Entropie $S(U,V,n_{1},\dots ,n_{r})$
Entropie $S$ und Volumen $V$	Minimum der inneren Energie $U(S,V,n_{1},\dots ,n_{r})$
Entropie $S$ und Druck $p$	Minimum der Enthalpie $H(S,p,n_{1},\dots ,n_{r})$
Temperatur $T$ und Volumen $V$	Minimum der freien Energie $F(T,V,n_{1},\dots ,n_{r})$
Temperatur $T$ und Druck $p$	Minimum der Gibbs-Energie $G(T,p,n_{1},\dots ,n_{r})$

In diesem Abschnitt wurde vorausgesetzt, dass das System keine Arbeit außer Volumenänderungsarbeit leistet. Der folgende Abschnitt behandelt Systeme, die auch andere Formen von Arbeit leisten.

Gibbs-Energie und maximale Nicht-Volumenarbeit

Im Verlaufe eines Prozesses tauscht ein System in der Regel Wärme und Arbeit mit seiner Umgebung aus. Wie im Folgenden gezeigt wird, ist bei einem isothermen, isobaren und reversiblen Prozess die Abnahme der Gibbs-Energie des Systems zahlenmäßig gleich der vom System an der Umgebung geleisteten Arbeit, wenn die eventuell geleistete Volumenänderungsarbeit $p\,\mathrm {d} V$ nicht berücksichtigt wird.[Anm. 2]

Maximale Nicht-Volumenarbeit

Ändert sich die Enthalpie $H=U+p\,V$ eines Systems im Verlaufe eines Prozesses, so gilt für eine differentielle Enthalpieänderung allgemein

{\begin{alignedat}{3}\mathrm {d} H&=\mathrm {d} (U+pV)&&\\&=\mathrm {d} U&&\,+\,p\,\mathrm {d} V+V\,\mathrm {d} p\\&=\mathrm {d} Q+\mathrm {d} W&&\,+\,p\,\mathrm {d} V+V\,\mathrm {d} p\\&=\mathrm {d} Q+\mathrm {d} W_{V}+\mathrm {d} W_{N}&&\,+\,p\,\mathrm {d} V+V\,\mathrm {d} p\end{alignedat}}

.

Die Änderung der inneren Energie $\mathrm {d} U$ lässt sich nämlich nach dem Ersten Hauptsatz der Thermodynamik aufspalten in die ausgetauschte Wärme $\mathrm {d} Q$ und die ausgetauschte Arbeit $\mathrm {d} W$ . Die Arbeit wiederum lässt sich unterteilen in Volumenänderungsarbeit $\mathrm {d} W_{V}$ und andere Formen von Arbeit (beispielsweise mechanische, elektrische, chemische Arbeit), die als Nicht-Volumenarbeit $\mathrm {d} W_{N}$ zusammengefasst seien.

Falls der Prozess reversibel verläuft,

lässt sich nach dem Zweiten Hauptsatz die ausgetauschte Wärme durch die ausgetauschte Entropie ausdrücken: $\mathrm {d} Q=T\mathrm {d} S$ ,
ist die am System geleistete Volumenänderungsarbeit gegeben durch $\mathrm {d} W_{V}=-p\,\mathrm {d} V$ ,
wird die für die vorliegende Zustandsänderung maximal mögliche Arbeit am System geleistet und es ist $\mathrm {d} W_{N}=\mathrm {d} W_{N_{\mathrm {max} }}$ .

In diesem reversiblen Fall lässt sich die obige Gleichung schreiben als

{\begin{alignedat}{5}\mathrm {d} H&=T\mathrm {d} S&&\,-\,p\,\mathrm {d} V&&\,+\,\mathrm {d} W_{N_{\mathrm {max} }}&&\,+\,p\,\mathrm {d} V&&\,+\,V\,\mathrm {d} p\\&=T\mathrm {d} S&&&&\,+\,\mathrm {d} W_{N_{\mathrm {max} }}&&&&\,+\,V\,\mathrm {d} p\end{alignedat}}

.

Für die mit dem Prozess verbundene Änderung der Gibbs-Energie des Systems schließlich gilt gemäß deren Definition und unter Verwendung des soeben hergeleiteten Ausdrucks für $\mathrm {d} H$ :

{\begin{alignedat}{6}\mathrm {d} G&=\mathrm {d} (H-TS)&&&&&\\&=\mathrm {d} H&&&\,-\,&T\mathrm {d} S&\,-\,S\mathrm {d} T\\&=(T\mathrm {d} S&\,+\,&\mathrm {d} W_{N_{\mathrm {max} }}+V\mathrm {d} p)&\,-\,&T\mathrm {d} S&\,-\,S\mathrm {d} T\\&=&&\mathrm {d} W_{N_{\mathrm {max} }}+V\mathrm {d} p&&&\,-\,S\mathrm {d} T\end{alignedat}}

Falls der Prozess unter isothermen ( $\mathrm {d} T=0$ ) und isobaren ( $\mathrm {d} p=0$ ) Bedingungen verläuft, vereinfacht sich dies zu

\mathrm {d} G=\mathrm {d} W_{N_{\mathrm {max} }}

.[8]

Möchte man die vom System geleistete und der Umgebung zur Verfügung gestellte Arbeit positiv zählen, ist ihr Vorzeichen umzukehren

\mathrm {d} W'_{N_{\mathrm {max} }}=-\mathrm {d} W_{N_{\mathrm {max} }}

und es ist die freigesetzte Arbeit

\mathrm {d} W'_{N_{\mathrm {max} }}=-\mathrm {d} G

.

Ändert sich also im Zuge eines isothermen, isobaren und reversiblen Prozesses die Gibbs-Energie eines Systems, dann ist die Abnahme der Gibbs-Energie des Systems gleich der vom System während des Prozesses an die Umgebung abgegebenen Nicht-Volumenarbeit. Wird umgekehrt Nicht-Volumenarbeit am System geleistet, nimmt dessen Gibbs-Energie um den entsprechenden Betrag zu.[Anm. 3]

Dieser Zusammenhang lässt sich beispielsweise zur Berechnung der elektrischen Arbeit nutzen, die aus elektrochemischen Zellen oder aus Brennstoffzellen gewonnen werden kann.[9] Umgekehrt kann aus der Messung der elektrischen Arbeit einer Reaktion deren Gibbssche Reaktionsenergie $\Delta _{r}G$ bestimmt werden, falls sich mit dieser Reaktion eine elektrochemische Zelle betreiben lässt. Durch Anlegen einer geeignet gewählten Gegenspannung lässt sich die Zelle nahe dem Gleichgewichtszustand betreiben, so dass die elektrochemische Reaktion praktisch reversibel abläuft und die maximal mögliche elektrische Arbeit liefert.

Mit einem ähnlichen Argument wie oben lässt sich zeigen, dass derselbe Zusammenhang zwischen Nicht-Volumenarbeit und Gibbs-Energie auch für Prozesse gilt, die vorübergehend andere, vom Anfangs- und Endzustand abweichende Temperaturen und Drücke annehmen.[10]^{:68, 72ff} Dies ist beispielsweise der Fall bei Verbrennungsreaktionen. Wählt man als Endzustand einen Zustand, in dem das System nach der Verbrennung wieder die Ausgangstemperatur – beispielsweise 20 °C – angenommen hat, dann wird der Gesamtprozess inklusive Aufheizung und Abkühlung durch die Gibbs-Energien der Ausgangsstoffe und Produkte bei 20 °C beschrieben. Allerdings ist eine freie Verbrennung eine Reaktion, die fernab vom Gleichgewichtszustand und damit irreversibel stattfindet, so dass sie nicht die maximal mögliche Arbeitsleistung liefern kann. Soll ein Prozess, in dem das System vorübergehend auch andere Temperaturen als die Temperatur $T$ von Anfangs- und Endzustand und andere Drücke als den Druck $p$ von Anfangs- und Endzustand annimmt, reversibel geführt werden, so ist insbesondere sicherzustellen, dass trotz der Veränderlichkeit von Temperatur und Druck der Wärmeaustausch mit dem Wärmereservoir bei der Temperatur $T$ und der Volumenaustausch mit dem Druckreservoir beim Druck $p$ stattfindet.

Läuft ein isothermer, isobarer und nicht reversibler Prozess ab, dann wird nicht die gesamte Abnahme der Gibbs-Energie in Nicht-Volumenarbeit umgesetzt, ein Teil wird als Wärme abgegeben. In diesem Fall ist die Ausbeute an Nicht-Volumenarbeit $\mathrm {d} W'_{N_{\mathrm {irrev} }}$ geringer:

-\mathrm {d} G=\mathrm {d} W'_{N_{\mathrm {max} }}>\mathrm {d} W'_{N_{\mathrm {irrev} }}

.

Erstes Beispiel

Als Beispiel für die maximale Nicht-Volumenarbeit einer chemischen Reaktion sei ermittelt, welche Nicht-Volumenarbeit ein Organismus bei einer Körpertemperatur von 37 °C und Atmosphärendruck aus der Verbrennung von einem Mol Glucose gewinnen kann, um damit seine Funktionen (wie etwa die letztlich elektrische Nerven- und Muskeltätigkeit) aufrecht zu erhalten. Aus einschlägigen Tabellen entnimmt man für Glucose die Verbrennungsenthalpie

\Delta _{c}H=-2808\ \mathrm {\tfrac {kJ}{mol}}

(der Index c steht für combustion) und die mit der Verbrennung verbundene Entropieänderung

\Delta _{c}S=+182{,}4\ \mathrm {\tfrac {J}{K\ mol}}

.

Die Zahlen gelten streng genommen für 25 °C und werden hier näherungsweise für 37 °C verwendet. Da Enthalpie und Entropie Zustandsgrößen sind und daher nur vom Anfangs- und Endzustand abhängen, gelten diese Zahlenwerte für die Oxidation von Glucose unabhängig davon, ob sie in einer offenen Verbrennung oder – wie hier – in einer enzymatisch katalysierten Reaktion erfolgt. Die Gibbssche Reaktionsenthalpie ist

\Delta _{c}G=\Delta _{c}H-T\ \Delta _{c}S=-2808\ \mathrm {\tfrac {kJ}{mol}} -(310\ \mathrm {K} )\ (182{,}4\ \mathrm {\tfrac {J}{K\ mol}} )=-2865\ \mathrm {\tfrac {kJ}{mol}}

.

Aus der Verbrennung von einem Mol Glucose können also maximal $2865\ \mathrm {kJ}$ Nicht-Volumenarbeit gewonnen werden.[11] Läuft der Verbrennungsprozess nicht-reversibel ab, ist die gewinnbare Arbeit je nach Ausmaß der Irreversibilität geringer.

Zweites Beispiel

In der weiter unten diskutierten Herleitung der barometrischen Höhenformel tritt neben einem druckabhängigen Term auch ein höhenabhängiger auf: Die Gibbs-Energie des betrachteten Volumenelements erhöht sich um den Betrag der Hubarbeit, die beim Hochheben des Volumenelements im Schwerefeld geleistet wird.

Prozesse ohne Nicht-Volumenarbeit

Läuft ein isothermer, isobarer und reversibler Prozess ab, in dessen Verlauf das System keine Nicht-Volumenarbeit leistet (also keinerlei Arbeit, außer eventuell Volumenänderungsarbeit), dann ändert sich bei diesem Prozess die freie Energie des Systems nicht:

-\mathrm {d} G=\mathrm {d} W'_{N_{\mathrm {max} }}=0

.

Wird beispielsweise ein Teil einer gegebenen Menge Wasser durch Zuführen von Latentwärme in eine Dampfphase überführt, die mit dem restlichen Wasser bei gleicher Temperatur und gleichem Druck im Gleichgewicht steht, dann ist dieser isotherme, isobare und reversible Prozess zwar (wegen der Ausdehnung des Wassers beim Verdampfen) mit Volumenänderungsarbeit verbunden, er leistet aber keine Nicht-Volumenarbeit. Folglich hat der Dampf dieselbe molare Gibbs-Energie wie das Wasser, mit dem er im Gleichgewicht steht.[12]^:86 Die Gleichheit der molaren Gibbs-Energie in verschiedenen Phasen einer Substanz, die miteinander im Gleichgewicht stehen, wird später noch eingehender behandelt.

Läuft ein isothermer, isobarer und irreversibler Prozess ab, in dessen Verlauf das System keine Nicht-Volumenarbeit leistet

\mathrm {d} W'_{N_{\mathrm {irrev} }}=0

,

dann gilt die Ungleichung (siehe oben)

-\mathrm {d} G=\mathrm {d} W'_{N_{\mathrm {max} }}>\mathrm {d} W'_{N_{\mathrm {irrev} }}=0

,

oder

\mathrm {d} G<0

.

Spontan ablaufende Prozesse sind stets irreversibel. Läuft also ein isothermer und isobarer Prozess, in dessen Verlauf das System keine Nicht-Volumenarbeit leistet, spontan ab, dann ist er mit einer Abnahme der Gibbs-Energie verbunden.[12]^:90 Dieses Ergebnis ist bereits aus dem vorigen Abschnitt bekannt.

Ableitungen der Gibbs-Energie

Da die Änderung der Gibbs-Energie ein wichtiger Aspekt bei ihrer Anwendung auf thermodynamische Prozesse ist, wird in diesem Abschnitt untersucht, wie sie von ihren Variablen $T$ , $p$ und $n_{1},\dots ,n_{r}$ abhängt. Zur Vorbereitung werden zunächst die Ableitungen der inneren Energie und einige damit zusammenhängende Definitionen betrachtet.

Die Ableitungen der inneren Energie

Geht man von der inneren Energie $U$ als Funktion ihrer natürlichen Variablen $S,V,n_{1},\dots ,n_{r}$ [Anm. 4] aus und bildet ihr totales Differential, erhält man:

\mathrm {d} U(S,V,n_{1},\dots ,n_{r})=\left({\frac {\partial U}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}\mathrm {d} S+\left({\frac {\partial U}{\partial V}}\right)_{S,n_{1},\dots ,n_{r}}\mathrm {d} V\,+\,\sum _{i=1}^{r}\left({\frac {\partial U}{\partial n_{i}}}\right)_{S,V,n_{j\neq i}}\mathrm {d} n_{i}

.

Die hierbei auftretenden partiellen Ableitungen werden in der Thermodynamik als die Definitionen von Temperatur $T$ , Druck $p$ und chemischem Potential der i-ten Substanz $\mu _{i}$ interpretiert:[3]^:35

T:=\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}

p:=-\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial V}}\right)_{S,n_{1},\dots ,n_{r}}

\mu _{i}:=\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{S,V,n_{j\neq i}}

.

Mit diesen Definitionen lässt sich das Differential der inneren Energie auch schreiben als

\mathrm {d} U(S,V,n_{1},\dots ,n_{r})=T\,\mathrm {d} S-p\,\mathrm {d} V\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} n_{i}

.

Die Ableitungen der Gibbs-Energie

Das totale Differential der Gibbs-Energie $G$ als Funktion ihrer natürlichen Variablen $T,p,n_{1},\dots ,n_{r}$ ist einerseits formal

\mathrm {d} G(T,p,n_{1},\dots ,n_{r})=\left({\frac {\partial G}{\partial T}}\right)_{p,n_{1},\dots ,n_{r}}\mathrm {d} T+\left({\frac {\partial G}{\partial p}}\right)_{T,n_{1},\dots ,n_{r}}\mathrm {d} p\,+\,\sum _{i=1}^{r}\left({\frac {\partial G}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}\mathrm {d} n_{i}\quad (*)

.

und andererseits, unter Benutzung ihrer Definition und Verwendung des soeben hergeleiteten Ausdrucks für $\mathrm {d} U$ :

{\begin{alignedat}{13}\mathrm {d} G&\,=\mathrm {d} (U&&&&&\,+\,&pV&&&\,-\,&TS)&&\\&\,=\mathrm {d} U&&&&&\,+\,&p\,\mathrm {d} V&\,+\,&V\,\mathrm {d} p&\,-\,&T\,\mathrm {d} S&\,-\,&S\mathrm {d} T\\&\,=T\,\mathrm {d} S&\,-\,&p\,\mathrm {d} V&\,+\,&\sum \mu _{i}\,\mathrm {d} n_{i}&\,+\,&p\,\mathrm {d} V&\,+\,&V\,\mathrm {d} p&\,-\,&T\,\mathrm {d} S&\,-\,&S\mathrm {d} T\\&\,=&&&&\sum \mu _{i}\,\mathrm {d} n_{i}&&&\,+\,&V\,\mathrm {d} p&&&\,-\,&S\mathrm {d} T\\\end{alignedat}}

also umgestellt

\mathrm {d} G=-S\,\mathrm {d} T+V\,\mathrm {d} p\,+\,\sum \mu _{i}\,\mathrm {d} n_{i}\quad (*)

so dass aus dem Vergleich der Koeffizienten in den markierten Gleichungen $(*)$ folgt[13]

\left({\frac {\partial G}{\partial T}}\right)_{p,n_{1},\dots ,n_{r}}=-S

,

sowie

\left({\frac {\partial G}{\partial p}}\right)_{T,n_{1},\dots ,n_{r},\dots }=V

und

\left({\frac {\partial G}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}=\mu _{i}

.

Diese einfachen Zusammenhänge werden in den folgenden Abschnitten näher diskutiert.

Die Herleitung zeigt gleichzeitig, wie die Addition der Terme $-T\,S$ und $p\,V$ die Liste der unabhängigen Variablen von $(S,V,\dots )$ in $(T,p,\dots )$ ändert,[13] indem dadurch im totalen Differential die von $\mathrm {d} S$ und $\mathrm {d} V$ abhängigen Terme entfernt und dafür von $\mathrm {d} T$ und $\mathrm {d} p$ abhängige Terme hinzugefügt werden.

Die zweite der markierten Gleichungen ist eine „differentielle Fundamentalfunktion“,[7]^{:13, 48} nämlich die häufig benötigte differentielle Gibbs-Energie als Funktion ihrer natürlichen Variablen:[Anm. 4]

\mathrm {d} G(T,p,n_{1},\dots ,n_{r})=-S\,\mathrm {d} T+V\mathrm {d} p\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} n_{i}

.

Gibbs-Energie und chemisches Potential

Man betrachte eine homogene Phase mit der Temperatur $T$ und dem Druck $p$ , die aus einer Mischung von $r$ Substanzen besteht, wobei jeweils die $i$ -te Substanz in der Menge $n_{i}$ vorhanden ist. Aus der oben hergeleiteten Gleichung[Anm. 5]

\left({\frac {\partial G}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}=\mu _{i}

folgt eine anschauliche Interpretation des chemischen Potentials $\mu _{i}$ :

Das chemische Potential $\mu _{i}$ der $i$ -ten Komponente der Phase gibt an, um welchen (infinitesimalen) Betrag $\mathrm {d} G$ sich die Gibbs-Energie der Phase ändert, wenn die Menge der $i$ -ten Komponente in der Phase sich um den (infinitesimalen) Betrag $\mathrm {d} n_{i}$ ändert, wobei die Temperatur $T$ , der Druck $p$ und die Mengen $n_{j}$ der übrigen Komponenten konstant gehalten werden. Die Menge der $i$ -ten Komponente kann sich beispielsweise im Zuge einer in der Phase ablaufenden chemischen Reaktion ändern, oder weil sie der Phase aus der Umgebung (das kann auch eine andere Phase des Systems sein) zugeführt wird.

Der Übergang von der infinitesimalen Größe $\mathrm {d} G$ zur gesamten Gibbs-Energie $G$ des Systems scheint zunächst eine Integration zu erfordern. Diese wäre außerdem schwierig, weil $\mathrm {d} G$ in komplizierter Weise von den vorhandenen Substanzmengen $n_{1},\dots ,n_{r}$ abhängen kann, die sich ihrerseits im Verlaufe des Prozesses in komplizierter Weise ändern können. Es stellt sich jedoch heraus, dass der Zusammenhang zwischen $\mathrm {d} G$ (beziehungsweise den $\mu _{i}$ ) und $G$ überraschend einfach ist.

Ausgangspunkt der Betrachtungen[10]^:93 ist die oben hergeleitete allgemeingültige differentielle Fundamentalfunktion

\mathrm {d} G=-S\,\mathrm {d} T+V\,\mathrm {d} p+\mu _{1}\,\mathrm {d} n_{1}+\dots +\mu _{r}\,\mathrm {d} n_{r}

.

Man denke sich nun die Größe der Phase vervielfacht. Bei diesem Vorgang bleiben die Temperatur und der Druck unverändert, da sie intensive Größen sind. In diesem Fall sind also $\mathrm {d} T=0$ und $\mathrm {d} p=0$ und das Differential vereinfacht sich zu

\mathrm {d} G=\mu _{1}\,\mathrm {d} n_{1}+\dots +\mu _{r}\,\mathrm {d} n_{r}

.

Da die chemischen Potentiale $\mu _{1},\dots ,\mu _{r}$ ebenfalls intensive Größen sind, bleiben sie auch unverändert. Die direkte Integration des Differentials liefert daher

{\begin{aligned}\Delta G=\int \mathrm {d} G&=\int \mu _{1}\,\mathrm {d} n_{1}+\dots +\int \mu _{r}\,\mathrm {d} n_{r}\\&=\mu _{1}\int \mathrm {d} n_{1}+\dots +\mu _{r}\int \mathrm {d} n_{r}\\&=\mu _{1}\Delta n_{1}+\dots +\mu _{r}\Delta n_{r},\end{aligned}}

weil die $\mu _{1},\dots ,\mu _{r}$ als konstante Größen vor die jeweiligen Integrale gezogen werden können.

Wird die Phase auf $k$ -fache Größe vermehrt, dann nehmen auch die Zahlenwerte der extensiven Größen $G$ , $n_{1}$ … $n_{r}$ auf das $k$ -fache zu und es gilt

\Delta G=k\,G-G=(k-1)\,G

\Delta n_{i}=k\,n_{i}-n_{i}=(k-1)\,n_{i}

Einsetzen in die vorhergehende Gleichung führt auf

(k-1)G=\mu _{1}(k-1)n_{1}+\dots +\mu _{r}(k-1)n_{r}

und damit

G=n_{1}\mu _{1}+\dots +n_{r}\mu _{r}

.

Es besteht also ein einfacher Zusammenhang zwischen der Gibbs-Energie der Phase und den chemischen Potentialen der in der Phase enthaltenen Substanzen:

Wird jedes chemische Potential

\mu _{i}

mit der Menge

n_{i}

der betreffenden Substanz

i

multipliziert und die Summe über alle Substanzen gebildet, ist das Ergebnis gleich der Gibbs-Energie der Phase.[10]^:94

Sowohl $G$ als auch die $\mu _{i}$ sind dabei jeweils nur bis auf eine Konstante bestimmt.

Division durch die Gesamt-Stoffmenge $n$ der Phase liefert die oft benutzte molare Gibbs-Energie

{\frac {G}{n}}={\frac {n_{1}}{n}}\mu _{1}+\dots +{\frac {n_{r}}{n}}\mu _{r}=x_{1}\mu _{1}+\dots +x_{r}\mu _{r}

mit den Stoffmengenanteilen $x_{i}=n_{i}/n$ .

Für ein System, das nur aus einer einzigen Substanz besteht ( $r=1$ ) ist insbesondere

{\frac {G}{n}}=\mu

.

In einem Mehrkomponentensystem sind die chemischen Potentiale also identisch mit den partiellen molaren Gibbs-Energien des Systems. In einem Einkomponentensystem ist das chemische Potential identisch mit der molaren Gibbs-Energie des Systems.[3]^:168

Chemisches Potential in Phasen, die im Gleichgewicht stehen

Thermodynamische Potentiale nehmen in der Regel in den verschiedenen Phasen eines Systems unterschiedliche Werte an. Beispielsweise unterscheiden sich die molaren Enthalpien von Wasser und Wasserdampf, die im Gleichgewicht stehen, um den Betrag der Verdampfungsenthalpie des Wassers. Das chemische Potential hingegen nimmt in allen Phasen eines im Gleichgewicht stehenden Systems denselben Wert an.

Zum Beweis betrachte man ein einkomponentiges aus mehreren Phasen bestehendes, im Gleichgewicht befindliches System und nehme zunächst an, das chemische Potential habe an verschiedenen Orten $A$ und $B$ im System unterschiedliche Werte $\mu _{A}$ beziehungsweise $\mu _{B}$ . Denkt man sich eine Substanzmenge $\mathrm {d} n$ von Ort $A$ nach Ort $B$ transportiert, ändert sich die Gibbs-Energie an Ort $A$ um den Betrag $-\mu _{A}\mathrm {d} n$ und an Ort $B$ um den Betrag $+\mu _{B}\mathrm {d} n$ , die gesamte Gibbs-Energie des Systems ändert sich also um $\mathrm {d} G=(\mu _{B}-\mu _{A})\mathrm {d} n$ . Ist $\mu _{B}<\mu _{A}$ , dann ist die Änderung der Gibbs-Energie negativ und der Transport läuft spontan ab, im Widerspruch zur Annahme, dass sich das System bereits im Gleichgewicht befinde. Das System kann sich also nur im Gleichgewicht befinden, wenn $\mu _{A}=\mu _{B}$ ist.[14]

Da die beiden verglichenen Orte in verschiedenen Phasen aber auch in derselben Phase liegen können, folgt die Gleichheit des chemischen Potentials in allen Phasen, aber auch an allen Stellen innerhalb jeder Phase.[14]

Da im betrachteten Fall einer einzelnen Substanz das chemische Potential identisch ist mit der molaren Gibbs-Energie, folgt auch die Konstanz der molaren Gibbs-Energie in allen Phasen.

Temperaturabhängigkeit der Gibbs-Energie

Temperaturabhängigkeit

Aus der oben hergeleiteten Gleichung

\left({\frac {\partial G}{\partial T}}\right)_{p,n_{1},\dots ,n_{r}}=-S

folgt unmittelbar, dass die Temperaturabhängigkeit der Gibbs-Energie bei konstantem Druck und konstanten Stoffmengen gegeben ist durch das Negative der Entropie des Systems. Da die Entropie nach dem Dritten Hauptsatz der Thermodynamik stets positiv ist, nimmt die Gibbs-Energie unter diesen Bedingungen stets ab, wenn die Temperatur zunimmt. Bei Gasen mit ihrer hohen Entropie ist die Temperaturabhängigkeit der Gibbs-Energie größer als bei Flüssigkeiten oder Festkörpern.[15]

Division durch die Stoffmenge der Phase liefert die entsprechende Gleichung für die molaren Größen der Phase:

\left({\frac {\partial G_{m}}{\partial T}}\right)_{p,x_{1},\dots ,x_{r-1}}=-S_{m}

Beispiel

Als ein Beispiel für die Temperaturabhängigkeit betrachte man Eis und flüssiges Wasser, die im Gleichgewicht stehen. Die den beiden Phasen gemeinsame Temperatur sei also die dem gemeinsamen Druck entsprechende Schmelztemperatur (beispielsweise 0 °C, wenn der Druck der Atmosphärendruck ist). Da Gleichgewicht vorausgesetzt wird, haben beide Phasen dieselbe molare Gibbs-Energie:

G_{m,\ \mathrm {Eis} }(T)=G_{m,\ \mathrm {Wasser} }(T)

.

Erhöht man bei konstant gehaltenem Druck die Temperatur, dann ändern sich die molaren Gibbs-Energien proportional zum Negativen ihrer jeweiligen molaren Entropien:

{\begin{alignedat}{7}&G_{m,\ \mathrm {Eis} }(T')&&\,=\,G_{m,\ \mathrm {Eis} }(T)&&-S_{m,\ \mathrm {Eis} }&&\mathrm {d} T\\&G_{m,\ \mathrm {Wasser} }(T')&&\,=\,G_{m,\ \mathrm {Wasser} }(T)&&-S_{m,\ \mathrm {Wasser} }&&\mathrm {d} T.\end{alignedat}}

Da das flüssige Wasser im Vergleich zum Eis mit seiner Gitterstruktur die größere molare Entropie besitzt, nimmt seine molare Gibbs-Energie bei Temperaturerhöhung schneller ab, und es hat bei der erhöhten Endtemperatur schließlich eine kleinere molare Gibbs-Energie als das Eis. Das Gleichgewicht zwischen beiden Phasen ist also gestört. Es könnte wiederhergestellt werden, indem entweder das Eis schmilzt und die kleinere molare Gibbs-Energie von Wasser annimmt, oder indem das Wasser gefriert und die größere molare Gibbs-Energie von Eis annimmt. Da beim Schmelzvorgang (bei konstantem Druck und konstant gehaltener neuer Temperatur) die Gibbs-Energie des Gesamtsystems abnimmt, ist es der Schmelzprozess, den das System auswählt und spontan durchläuft, bis sich ein neues Gleichgewicht eingestellt hat.

Wird umgekehrt die Temperatur verringert, nimmt die molare Gibbs-Energie des Wassers stärker zu als die des Eises und das gestörte Gleichgewicht wird spontan wiederhergestellt, indem das Wasser gefriert und sich der kleineren molaren Gibbs-Energie des Eises angleicht.

Druckabhängigkeit der Gibbs-Energie

Druckabhängigkeit

Aus der oben hergeleiteten Gleichung

\left({\frac {\partial G}{\partial p}}\right)_{T,n_{1},\dots ,n_{r}}=V

folgt unmittelbar, dass die Druckabhängigkeit der Gibbs-Energie bei konstanter Temperatur und konstanten Stoffmengen durch das Volumen des Systems gegeben ist. Da das Volumen immer positiv ist, nimmt die Gibbs-Energie unter diesen Bedingungen stets zu, wenn der Druck zunimmt.

Division durch die Stoffmenge der Phase liefert die entsprechende Gleichung für die molaren Größen der Phase:

\left({\frac {\partial G_{m}}{\partial p}}\right)_{T,x_{1},\dots ,x_{r-1}}=V_{m}

.

Beispiel

Als ein Beispiel für die Druckabhängigkeit betrachte man wieder Eis und flüssiges Wasser, die im Gleichgewicht stehen. Da Gleichgewicht vorausgesetzt wird, haben beide Phasen dieselbe molare Gibbs-Energie:

G_{m,\ \mathrm {Eis} }(p)=G_{m,\ \mathrm {Wasser} }(p)

Erhöht man bei konstant gehaltener Temperatur den Druck, dann ändern sich die molaren Gibbs-Energien proportional zum jeweiligen molaren Volumen:

{\begin{alignedat}{7}&G_{m,\ \mathrm {Eis} }(p')&&\,=\,G_{m,\ \mathrm {Eis} }(p)&&+V_{m,\ \mathrm {Eis} }&&\mathrm {d} p\\&G_{m,\ \mathrm {Wasser} }(p')&&\,=\,G_{m,\ \mathrm {Wasser} }(p)&&+V_{m,\ \mathrm {Wasser} }&&\mathrm {d} p.\end{alignedat}}

Da das Eis im Vergleich zum flüssigen Wasser das größere molare Volumen besitzt, nimmt seine molare Gibbs-Energie bei Druckerhöhung schneller zu, und es hat beim erhöhten Enddruck schließlich eine höhere molare Gibbs-Energie als das Wasser. Das Gleichgewicht zwischen beiden Phasen ist gestört. Es wird wiederhergestellt, indem das Eis schmilzt und die kleinere molare Gibbs-Energie von Wasser annimmt. Da durch diesen Schmelzvorgang (bei konstanter Temperatur und konstant gehaltenem neuem Druck) die gesamte Gibbs-Energie des Systems abnimmt, läuft das Schmelzen spontan ab.

Trotz konstant gehaltener Temperatur liegt das unter erhöhtem Druck stehende System jetzt vollständig flüssig vor. Die Temperatur müsste also verringert werden, um beim neuen Druck wieder ein Gleichgewicht zwischen flüssigem Wasser und Eis zu ermöglichen: Durch die Druckerhöhung wurde die Schmelztemperatur gesenkt. Die Eigenschaften der Zustandsgröße Gibbs-Energie erlaubten diese Schlussfolgerung allein aus der Kenntnis der molaren Volumina von Eis und flüssigem Wasser.

Wird umgekehrt der Druck verringert, nimmt die molare Gibbs-Energie des Eises schneller ab als die des Wassers und das gestörte Gleichgewicht wird spontan wiederhergestellt, indem das Wasser gefriert und sich der kleineren molaren Gibbs-Energie des Eises angleicht.

Folgerungen

Ist die Gibbs-Energie bei einem Referenzdruck, beispielsweise dem Standarddruck $p^{\circ }$ bekannt, lässt sie sich für beliebige andere Drücke $p$ durch Integration ermitteln:

G(p)=G(p^{\circ })+\int _{p^{\circ }}^{p}V\,\mathrm {d} p

.

Für die molare Gibbs-Energie gilt entsprechend:

G_{m}(p)=G_{m}(p^{\circ })+\int _{p^{\circ }}^{p}V_{m}\,\mathrm {d} p

.

Bei Flüssigkeiten und Festkörpern ist das molare Volumen $V_{m}$ nur in geringem Maße mit dem Druck veränderlich. $V_{m}$ kann dann näherungsweise als konstant angesehen und vor das Integral gezogen werden:

G_{m}(p)=G_{m}(p^{\circ })+(p-p^{\circ })\,V_{m}

.

Bei nicht allzu extremen Druckzunahmen ist $(p-p^{\circ })\,V_{m}$ in der Regel vernachlässigbar und die Gibbs-Energie von Flüssigkeiten und Festkörpern ist praktisch druckunabhängig:[16]

G_{m}(p)=G_{m}(p^{\circ })

Bei Gasen andererseits ist das molare Volumen zu stark veränderlich, als dass es konstant gesetzt werden dürfte. Hier muss das Integral ausgewertet werden.

Gibbs-Energie des idealen Gases

Bei idealen Gasen lässt sich das Integral sofort berechnen, da das molare Volumen als

V_{m}={\frac {R\,T}{p}}

ausgedrückt und in das Integral eingesetzt werden kann:

{\begin{aligned}G_{m}(p)&=G_{m}(p^{\circ })+R\,T\,\int _{p^{\circ }}^{p}{\frac {1}{p}}\mathrm {d} p\\&=G_{m}(p^{\circ })+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right).\end{aligned}}

Für ein System, das nur aus einer einzigen Substanz besteht, ist die molare Gibbs-Energie $G_{m}$ identisch mit dem chemischen Potential $\mu$ der Substanz (siehe oben) und es gilt[17]

\mu =\mu ^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)

,

worin die molare Gibbs-Energie der Substanz im Standardzustand, $G_{m}(p^{\circ })$ , jetzt als chemisches Potential der Substanz im Standardzustand, $\mu ^{\circ }$ , bezeichnet wird.

Das chemische Potential eines idealen Gases lässt sich also leicht in Abhängigkeit vom Druck berechnen. Dies findet vielfältige Anwendung, denn es lässt sich auf diese Weise nicht nur das chemische Potential näherungsweise idealer Gase ermitteln. Betrachtet man beispielsweise eine Flüssigkeit, die mit ihrem Dampf im Gleichgewicht steht, dann ist die molare Gibbs-Energie – und damit auch das chemische Potential – in beiden Phasen identisch (siehe oben), und das chemische Potential der Flüssigkeit ist daher bekannt, sofern der Dampf in hinreichend guter Näherung als ideales Gas behandelt werden darf.

Gibbs-Energie eines Lösungsmittels

Als Beispiel hierfür sei eine Lösung betrachtet, also eine Mischung aus einem Lösungsmittel und einer darin gelösten Substanz. Gemäß dem Raoultschen Gesetz ist der Dampfdruck $p$ des Lösungsmittels proportional zum Stoffmengenanteil $x$ , mit dem es in der Lösung vertreten ist:

p\,=\,c\,x

.

(In den meisten Fällen gilt das Raoultsche Gesetz nur im Grenzfall stark verdünnter Lösungen; es sei im Folgenden die Gültigkeit für die betrachtete Lösung vorausgesetzt.) Ändert man den Stoffmengenanteil des Lösungsmittels von $x_{0}$ auf $x$ , verhalten sich die zugehörigen Dampfdrücke $p_{0}$ und $p$ also wie die Stoffmengenanteile:

{\frac {p}{p_{0}}}\,=\,{\frac {x}{x_{0}}}

.

Setzt man ferner voraus, dass der Lösungsmitteldampf in hinreichender Näherung als ideales Gas behandelt werden darf, dann ist die Formel aus dem letzten Abschnitt anwendbar und für die chemischen Potentiale $\mu _{0}$ und $\mu$ des Dampfes über den beiden betrachteten Lösungsmittelanteilen gilt:

\mu =\mu _{0}+R\,T\,\ln \left({\frac {p}{p_{0}}}\right)=\mu _{0}+R\,T\,\ln \left({\frac {x}{x_{0}}}\right)

.

Wählt man als Ausgangspunkt das reine Lösungsmittel (durch einen Stern $^{*}$ gekennzeichnet), dann ist wegen $x_{0}=x^{*}=1$ das chemische Potential des Lösungsmitteldampfs über dem Lösungsmittel mit Anteil $x$ [12]^:125ff

\mu =\mu ^{*}+R\,T\,\ln(x)

.

Weil das Lösungsmittel mit seinem Dampf im Gleichgewicht steht, besitzt es dasselbe chemische Potential. Da der Stoffmengenanteil $x$ des Lösungsmittels kleiner als Eins ist, hat sein Logarithmus negatives Vorzeichen. Die Anwesenheit einer gelösten Substanz verringert also unter den genannten Voraussetzungen das chemische Potential des Lösungsmittels. Dies ist die Ursache für Erscheinungen wie Osmose, Gefrierpunktserniedrigung in Lösungen und Ähnliches.

Wird der Stoffmengenanteil der gelösten Substanz mit $x_{2}:=1-x$ bezeichnet, dann wird

{\begin{aligned}\mu &=\mu ^{*}+R\,T\,\ln(x)\\&=\mu ^{*}+R\,T\,\ln(1-x_{2})\\&\approx \mu ^{*}-R\,T\,x_{2},\end{aligned}}

das chemische Potential des Lösungsmittels nimmt also proportional zum Stoffmengenanteil der gelösten Substanz ab.[12]^:125ff[Anm. 6] Man beachte, dass die Änderung des chemischen Potentials des Lösungsmittels nicht von der Natur der gelösten Substanz abhängt, sondern nur von ihrem Stoffmengenanteil, siehe → kolligative Eigenschaft.

Gibbssche Mischungsenergie idealer Gase

Man betrachte einen Behälter mit zwei Kammern, in denen sich die reinen Gase $A$ beziehungsweise $B$ befinden. Ihre Stoffmengen seien $n_{\mathrm {A} }$ beziehungsweise $n_{\mathrm {B} }$ (mit $n_{\mathrm {A} }+n_{\mathrm {B} }=n$ ). Ihre Temperaturen $T$ seien gleich, ebenso ihre Drücke $p$ . Da die Gibbs-Energie eine extensive Größe ist, berechnet sich die Gibbs-Energie des Gesamtsystems als Summe der Gibbs-Energien beider Teilsysteme. Benutzt man die molaren Gibbs-Energien, die wiederum identisch mit den chemischen Potentialen sind, ergibt sich

G_{\mathrm {Anfang} }=n_{\mathrm {A} }\ G_{\mathrm {m,A} }+n_{\mathrm {B} }\ G_{\mathrm {m,B} }=n_{\mathrm {A} }\ \mu _{\mathrm {A} }+n_{\mathrm {B} }\ \mu _{\mathrm {B} }

.

Handelt es sich insbesondere um ideale Gase, dann ist die Gibbs-Energie unter Verwendung der im vorigen Abschnitt abgeleiteten Formel für das chemische Potential eines idealen Gases:

G_{\mathrm {Anfang} }=n_{\mathrm {A} }\left(\mu _{\mathrm {A} }^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)\right)+n_{\mathrm {B} }\left(\mu _{\mathrm {B} }^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)\right)

.

Entfernt man die Trennwand zwischen den Kammern, vermischen sich die Gase. Sie haben im vermischten Zustand die Partialdrücke $p_{\mathrm {A} }$ beziehungsweise $p_{\mathrm {B} }$ (mit $p_{\mathrm {A} }+p_{\mathrm {B} }=p$ ). Mit diesen Drücken wird die Gibbs-Energie des Systems im vermischten Endzustand[Anm. 7]

G_{\mathrm {Ende} }=n_{\mathrm {A} }\left(\mu _{\mathrm {A} }^{\circ }+R\,T\,\ln \left({\frac {p_{\mathrm {A} }}{p^{\circ }}}\right)\right)+n_{\mathrm {B} }\left(\mu _{\mathrm {B} }^{\circ }+R\,T\,\ln \left({\frac {p_{\mathrm {B} }}{p^{\circ }}}\right)\right)

.

Die Differenz zwischen den Gibbs-Energien im End- und Anfangszustand ist die Gibbssche Mischungsenergie $\Delta _{\mathrm {mix} }G$ :

\Delta _{\mathrm {mix} }G=G_{\mathrm {Ende} }-G_{\mathrm {Anfang} }=n_{\mathrm {A} }\ R\,T\,\ln \left({\frac {p_{\mathrm {A} }}{p}}\right)+n_{\mathrm {B} }\ R\,T\,\ln \left({\frac {p_{\mathrm {B} }}{p}}\right)

.

Gemäß dem Daltonschen Gesetz lässt sich der Partialdruck $p_{\mathrm {A} }$ ausdrücken als das Produkt aus Stoffmengenanteil $x_{\mathrm {A} }$ und Gesamtdruck $p$ :

p_{\mathrm {A} }=x_{\mathrm {A} }\ p

.

Außerdem ist aufgrund der Definition des Stoffmengenanteils

n_{\mathrm {A} }=x_{\mathrm {A} }\ n

,

und entsprechende Ausdrücke gelten jeweils auch für Gas $B$ . Damit wird die Gibbssche Mischungsenergie idealer Gase:

\Delta _{\mathrm {mix} }G=n\ R\,T\,(x_{\mathrm {A} }\ln x_{\mathrm {A} }+x_{\mathrm {B} }\ln x_{\mathrm {B} })

.

Da die Stoffmengenanteile gemäß ihrer Definition im betrachteten Fall immer kleiner als Eins sind, werden die Logarithmen stets negativ, und auch die Gibbssche Mischungsenergie ist immer negativ. Die Gibbs-Energie des Gesamtsystems idealer Gase nimmt beim Vermischen also immer ab und das Vermischen idealer Gase ist daher ein freiwillig ablaufender Vorgang, was auch der Erfahrung mit realen aber näherungsweise idealen Gasen entspricht.[18]

Mischt man stark nicht-ideale Substanzen, ergeben sich andere Formeln für die Gibbssche Mischungsenergie. Sie kann dann unter Umständen sogar positive Werte annehmen. In einem solchen Fall entmischt sich eine Mischung freiwillig, die beteiligten Komponenten sind nicht mischbar.[19] Nimmt die Gibbssche Mischungsenergie nur in einem bestimmten Bereich von Zusammensetzungen der Mischung positive Werte an, ist die Mischung nur für diese Zusammensetzungen instabil – es liegt eine Mischungslücke vor.

Im betrachteten Fall nicht-reagierender idealer Gase blieben die Stoffmengen beider Komponenten beim Mischungsvorgang konstant. Wenn die gemischten Substanzen chemisch miteinander reagieren können, sind die Stoffmengen variabel. Sie stellen sich dann freiwillig so ein, dass die Gibbssche Mischungsenergie den kleinsten mit den Bedingungen der Reaktion verträglichen Wert annimmt. Der Zustand, der sich auf diese Weise einstellt, ist der Zustand chemischen Gleichgewichts. Die Lage dieses Gleichgewichtszustands lässt sich bei Kenntnis der Gibbsschen Mischungsenergie des Systems also vorherberechnen.

Anwendung

Osmose

Der Effekt der Osmose zeigt sich beispielsweise, wenn ein Lösungsmittel, das gelöste Stoffe enthält, durch eine für das Lösungsmittel durchlässige aber für die gelösten Stoffe undurchlässige Membran von reinem Lösungsmittel getrennt ist. Reines Lösungsmittel fließt dann spontan durch die Membran in die Lösung, auch ohne dass ein Druckunterschied anliegt.

Zur näheren Erläuterung betrachte man eine Phase, die eine Mischung aus einem Lösungsmittel und gelösten Stoffen ist. Sie stehe über eine semipermeable, nur für das Lösungsmittel durchlässige Membran in Kontakt mit einer zweiten Phase, die aus dem reinen Lösungsmittel besteht. Ein Beispiel wären eine Phase mit Zuckerwasser und eine Phase mit reinem Wasser, die durch eine Cellophanfolie voneinander getrennt sind.[20] Temperatur und Druck seien auf beiden Seiten identisch.

In der Mischung hat das Lösungsmittel ein kleineres chemisches Potential als im reinen Zustand (man vergleiche die obige Diskussion der Gibbs-Energie eines Lösungsmittels). Die unterschiedlichen chemischen Potentiale des Lösungsmittels in den beiden Phasen setzen einen ausgleichenden Lösungsmittelfluss in Gang, der Lösungsmittel von der Seite mit dem höheren chemischen Potential auf die Seite mit dem geringeren chemischen Potential (nämlich auf die Seite mit der Mischung) transportiert.

Will man den osmotischen Transport unterbinden, muss man bewirken, dass das Lösungsmittel sowohl in der reinen Phase als auch in der Mischphase dasselbe chemische Potential hat. Dies kann dadurch geschehen, dass man von der Forderung beidseitig gleichen Drucks abgeht und den Druck in der Mischphase erhöht (während die Temperaturen identisch bleiben). Wie oben erläutert, erhöht eine Druckzunahme das chemische Potential. Der Zusatzdruck $\Pi$ , den man anlegen muss, um Gleichgewicht herzustellen heißt osmotischer Druck. Ist $p$ der Druck im reinen Lösungsmittel und $p^{\prime }$ der Druck in der Mischung, dann ist also im Gleichgewicht

\Pi =p'-p

.

Das chemische Potential des reinen Lösungsmittel sei mit $\mu _{p}^{*}$ bezeichnet; der Stern kennzeichnet die reine Substanz und der Index $p$ den Druck, unter dem die Substanz steht.

Für die Mischphase sei der einfacheren Behandlung wegen angenommen, dass es sich um eine ideale Mischung[Anm. 8] handelt. Dann ist das chemische Potential des Lösungsmittels (Stoffmengenanteil $x$ ) in der Mischphase unter dem Druck $p'$ gegeben durch[10]^:263

\mu _{p'}^{*}+R\,T\,\ln x

.

Im osmotischen Gleichgewicht sind die beiden chemischen Potentiale gleich:

\mu _{p}^{*}=\mu _{p'}^{*}+R\,T\,\ln x

,

oder umgestellt und unter Berücksichtigung der Druckabhängigkeit des chemischen Potentials des reinen Lösungsmittels:

{\begin{aligned}R\,T\,\ln x&=\mu _{p}^{*}-\mu _{p'}^{*}\\&=\int _{p'}^{p}V_{m}\ \mathrm {d} p,\end{aligned}}

wobei $V_{\mathrm {m} }$ das molare Volumen des reinen Lösungsmittels ist. Mit ${\overline {V}}_{\mathrm {m} }$ als dem Mittelwert des molaren Volumens über das Druckintervall $p-p'$ wird daraus:

R\,T\,\ln x={\overline {V}}_{\mathrm {m} }\,(p-p')=-{\overline {V}}_{\mathrm {m} }\ \Pi

.

Für den osmotischen Druck gilt also:

\Pi =-{\frac {R\,T}{{\overline {V}}_{\mathrm {m} }}}\,\ln x

.

Mit $\textstyle \sum x_{\mathrm {i} }$ als der Summe über die Stoffmengenanteile aller gelösten Substanzen ist

\Pi =-{\frac {R\,T}{{\overline {V}}_{\mathrm {m} }}}\,\ln(1-\sum x_{\mathrm {i} })

,

was sich für kleines $\textstyle \sum x_{\mathrm {i} }$ zu

\Pi \approx {\frac {R\,T}{{\overline {V}}_{\mathrm {m} }}}\,\sum x_{\mathrm {i} }

vereinfacht,[10]^:264 dem van-’t-Hoff’schen Gesetz. Der osmotische Druck[Anm. 9] hinreichend verdünnter Lösungen ist also proportional zur Summe der Stoffmengenanteile der gelösten Substanzen.

Clausius-Clapeyron-Gleichung

Bei der obigen Diskussion der Temperatur- und der Druckabhängigkeit der Gibbs-Energie wurde gezeigt, dass ein bestehendes Gleichgewicht zweier Phasen einer Substanz gestört wird, wenn entweder die Temperatur des Systems bei konstant gehaltenem Druck oder der Druck des Systems bei konstant gehaltener Temperatur geändert wird. Es ist jedoch möglich, Druck und Temperatur gemeinsam so zu ändern, dass die Phasen im Gleichgewicht bleiben, sofern die Änderungen $\mathrm {d} T$ und $\mathrm {d} p$ geeignet aufeinander abgestimmt sind.

Befindet sich das betrachtete System zweier Phasen $1$ und $2$ einer Substanz anfangs im Gleichgewicht, sind die spezifischen[Anm. 10] Gibbs-Energien der beiden Phasen gleich. Nach den Änderungen $\mathrm {d} T$ und $\mathrm {d} p$ sollen die Phasen ebenfalls im Gleichgewicht sein, ihre spezifischen Gibbs-Energien müssen daher – in der Regel mit geänderten Zahlenwerten – wiederum gleich sein. Die spezifischen Gibbs-Energien beider Phasen müssen sich also um denselben Betrag geändert haben:

\mathrm {d} g_{1}=\mathrm {d} g_{2}

.

Da das System nur aus einer einzigen Substanz besteht,[Anm. 11] reduziert sich die differentielle Gibbs-Funktion (siehe oben) auf den Ausdruck $\mathrm {d} g=-s\,\mathrm {d} T+v\,\mathrm {d} p$ , und aus

v_{1}\,\mathrm {d} p-s_{1}\,\mathrm {d} T=v_{2}\,\mathrm {d} p-s_{2}\,\mathrm {d} T

folgt die Clapeyron-Gleichung

{\frac {\mathrm {d} p}{\mathrm {d} T}}={\frac {s_{2}-s_{1}}{v_{2}-v_{1}}}

.

Die Differenz $s_{2}-s_{1}$ ist der Unterschied der spezifischen Entropien beider Phasen. Sie ist identisch mit der spezifischen Latent-Enthalpie $\Delta h$ , die einer Masseneinheit der Substanz bei der gegebenen Temperatur und dem gegebenen Druck zugeführt werden muss, um sie reversibel von Phase $1$ in Phase $2$ zu überführen, dividiert durch die vorliegende Temperatur $T$ :

s_{2}-s_{1}={\frac {\Delta h}{T}}

.

Einsetzen dieses Ausdrucks ergibt die Clausius-Clapeyron-Gleichung:[12]^:110ff

{\frac {\mathrm {d} p}{\mathrm {d} T}}\,=\,{\frac {\Delta h}{T\,\Delta v}}

.

Dampfdruck über Tropfen

Der Sättigungsdampfdruck einer Flüssigkeit bei einer gegebenen Temperatur ist jener Druck, bei dem die Flüssigkeit mit ihrem Dampf im Gleichgewicht steht. Dabei wird üblicherweise vorausgesetzt, dass die Flüssigkeitsoberfläche eben ist. Über gekrümmten Oberflächen nimmt der Sättigungsdampfdruck andere Werte an: Er ist über konvex gekrümmten Oberflächen (z. B. über Tropfen) höher und über konkav gekrümmten Oberflächen (z. B. über dem Meniskus in einer teilweise gefüllten Kapillare) geringer als über einer ebenen Oberfläche.

Die Ursache dafür ist der veränderte Druck, unter dem die Flüssigkeit bei gekrümmter Oberfläche steht. Bei ebener Oberfläche ist (da ja Gleichgewicht vorausgesetzt wird) der Druck in der Flüssigphase gleich dem Druck in der Dampfphase. Die Flüssigkeit in einem Tropfen des Radius $r$ steht jedoch unter einem höheren Druck, da die Oberflächenspannung $\gamma$ einen zusätzlichen kapillaren Druck

p_{\mathrm {k} }=2\gamma /r

im Tropfen erzeugt. Der Gesamtdruck im Tropfen ist die Summe aus dem Kapillardruck und dem von der Dampfphase auf den Tropfen ausgeübten Sättigungsdampfdruck. Gesucht ist der neue Sättigungsdampfdruck, der sich unter diesen veränderten Druckbedingungen über der gekrümmten Oberfläche einstellen muss, um das Gleichgewicht zu erhalten.

Die Druckabhängigkeit des Sättigungsdampfdrucks lässt sich durch Betrachtung der Druckabhängigkeit der chemischen Potentiale der Flüssigkeit $\mu _{\mathrm {l} }$ und des Dampfes $\mu _{\mathrm {g} }$ ermitteln (der Index l steht für liquid, der Index g für gas). In jedem Gleichgewicht von Flüssigkeit und Dampf sind die chemischen Potentiale der beiden Phasen gleich:

\mu _{\mathrm {g} }=\mu _{\mathrm {l} }

.

Geschieht eine Änderung, die in ein neues Gleichgewicht führt, ändern sich im Allgemeinen $\mu _{\mathrm {g} }$ und $\mu _{\mathrm {l} }$ , sie bleiben aber untereinander gleich, müssen sich also beide auf dieselbe Weise ändern:

\mathrm {d} \mu _{\mathrm {g} }=\mathrm {d} \mu _{\mathrm {l} }

.

Besteht die Änderung in einer Druckänderung $\mathrm {d} p_{\mathrm {l} }$ in der Flüssigkeit, dann ändert sich das chemische Potential der Flüssigkeit (siehe Druckabhängigkeit der Gibbs-Energie) dabei um

\mathrm {d} \mu _{\mathrm {l} }=V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }

,

wobei $V_{\mathrm {m,l} }$ das molare Volumen der Flüssigkeit ist. Ein entsprechender Ausdruck gilt für die Dampfphase und es folgt

V_{\mathrm {m,g} }\,\mathrm {d} p_{\mathrm {g} }=V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }

.

Aus dieser Gleichung lässt sich ermitteln, welche Druckänderung $\mathrm {d} p_{\mathrm {g} }$ in der Dampfphase zur Neueinstellung des Gleichgewichts notwendig ist, wenn der Druck in der Flüssigphase sich um $\mathrm {d} p_{\mathrm {l} }$ ändert.

Zur Vereinfachung sei angenommen, dass der Dampf sich wie ein ideales Gas verhält. Sein molares Volumen ist dann gegeben durch $V_{\mathrm {m,g} }=R\,T/p_{\mathrm {g} }$ und es gilt

{\frac {\mathrm {d} p_{\mathrm {g} }}{p_{\mathrm {g} }}}={\frac {V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }}{R\,T}}

Diese Formel wird nun integriert, vom Anfangszustand ohne zusätzlichen Druck bis zum Endzustand, in dem in der Flüssigkeit ein zusätzlicher Druck $\Delta p$ herrscht. Im Anfangszustand sind die Drücke im Dampf und in der Flüssigkeit gleich dem normalen Sättigungsdampfdruck $p_{0}$ . Im Endzustand herrscht in der Flüssigkeit der um $\Delta p$ erhöhte Druck $p_{0}+\Delta p$ ,[Anm. 12] im Dampf herrscht der zu bestimmende Druck $p$ :

\int _{p_{0}}^{p}{\frac {\mathrm {d} p_{\mathrm {g} }}{p_{\mathrm {g} }}}={\frac {1}{R\,T}}\int _{p_{0}}^{p_{0}+\Delta p}V_{\mathrm {m,l} }\,\mathrm {d} p_{\mathrm {l} }

.

Wird als weitere Vereinfachung angenommen, dass das molare Volumen der Flüssigkeit im betrachteten Druckbereich konstant (die Flüssigkeit also inkompressibel) ist, folgt

{\begin{aligned}\ln \left({\frac {p}{p_{0}}}\right)&={\frac {V_{\mathrm {m,l} }}{R\,T}}\,(p_{0}+\Delta p-p_{0})\\&={\frac {V_{\mathrm {m,l} }}{R\,T}}\,\Delta p\end{aligned}}

oder umgeformt[21]

p=p_{0}\,e^{\frac {V_{\mathrm {m,l} }\,\Delta p}{R\,T}}

.

Diese Formel beschreibt, wie der Sättigungsdampfdruck von $p_{0}$ auf $p$ zunimmt, wenn auf die Flüssigkeit ein zusätzlicher Druck $\Delta p$ ausgeübt wird, und zwar unabhängig davon, auf welche Weise der Druckanstieg $\Delta p$ in der Flüssigkeit erzeugt wurde.

Eine offene Wasseroberfläche beispielsweise ist dem Atmosphärendruck ausgesetzt statt nur ihrem eigenen Sättigungsdampfdruck; der Sättigungsdampfdruck in feuchter Atmosphärenluft ist daher geringfügig höher als in einer reinen Wasserdampfatmosphäre bei der gleichen Temperatur (Poynting-Effekt). So beträgt der Sättigungsdampfdruck reinen Wassers im Gleichgewicht mit einer nur aus Wasserdampf bestehenden Atmosphäre am Tripelpunkt 612 Pa. Wird der Dampfphase Luft hinzugefügt, bis der atmosphärische Gesamtdruck von 101325 Pa erreicht wird, ist der Gleichgewichts-Partialdruck des Wasserdampfs in der Mischung aus Dampf und Luft (in der so genannten „feuchten Luft“) wegen des gut 10⁵ Pa betragenden Druckanstiegs um 0,5 Pa höher als in der reinen Wasserdampfatmosphäre.[22][Anm. 13]

Ist der Druckanstieg auf Kapillarkräfte zurückzuführen, weil statt der Flüssigkeit mit ebener Oberfläche nun ein Tropfen des Radius $r$ betrachtet wird, dann ist $\Delta p=2\gamma /r$ und für den Sättigungsdampfdruck über dem Tropfen gilt[21]

p_{\mathrm {Tr} }=p_{0}\,e^{\frac {2\gamma \,V_{\mathrm {m,l} }}{R\,T\,r}}

Dies ist die Kelvingleichung. Über einem Wassertröpfchen mit 0,001 mm Radius beispielsweise ist bei 25 °C[23] der Sättigungsdampfdruck um den Faktor 1,001 größer als über einer ebenen Wasseroberfläche.[24] Über einem konkaven Meniskus mit demselben Radius ist der Sättigungsdampfdruck um den gleichen Faktor geringer.

Barometrische Höhenformel

Diese kurze alternative Herleitung der barometrischen Höhenformel demonstriert die Änderung der Gibbs-Energie eines Volumenelements ín einem Fluid, wenn sich der einwirkende hydrostatische Druck ändert und wenn Nicht-Volumenarbeit am Element geleistet wird.

Gegeben sei eine im Gleichgewicht befindliche vertikale Säule eines Fluids (zum Beispiel Wasser oder Luft) im homogenen Schwerefeld der Feldstärke ${\overline {g}}$ .[Anm. 14] Untersucht wird die Gibbs-Energie eines Volumenelements in Abhängigkeit von seiner Höhe in der Fluidsäule. Zu diesem Zweck wird angenommen, das Volumenelement sei von einem Punkt $A$ zu einem Punkt $B$ auf einer anderen Höhe transportiert worden. Die Änderung seiner spezifischen (also auf die Masse bezogenen) Gibbs-Energie $g$ bei diesem Prozess besteht aus zwei Beiträgen:

Die Veränderung des hydrostatischen Drucks $P$ entlang des Weges ändert die spezifische Gibbs-Energie um

\Delta g_{P}=\int _{A}^{B}v\,\mathrm {d} P

,

wobei $v$ das spezifische Volumen des Fluids unter dem jeweiligen Druck ist.

Die bei der Höhenänderung $\Delta h$ am Volumenelement geleistete (als reversibel angenommene) spezifische Hubarbeit ist Nicht-Volumenarbeit, sie erhöht die spezifische Gibbs-Energie des Volumenelements also um

\Delta g_{W}=\mathrm {d} w_{N_{\mathrm {max} }}=\int _{A}^{B}{\overline {g}}\,\mathrm {d} h

.

Insgesamt ändert sich die spezifische Gibbs-Energie bei der Höhenänderung um

\Delta g=\Delta g_{P}+\Delta g_{W}=\int _{A}^{B}v\,\mathrm {d} P+\int _{A}^{B}{\overline {g}}\,\mathrm {d} h

.

Da angenommen wird, die Fluidsäule befinde sich im Gleichgewicht, muss die spezifische Gibbs-Energie auf allen Höhen denselben Wert besitzen, es ist also $\Delta g=0$ , woraus folgt

v\,\mathrm {d} P+{\overline {g}}\,\mathrm {d} h=0

.

Umstellen und Einsetzen der Dichte $\textstyle \rho ={\frac {1}{v}}$ liefert

{\frac {\mathrm {d} P}{\mathrm {d} h}}=-{\frac {\overline {g}}{v}}=-{\overline {g}}\,\rho

.[12]^:109f

Dies ist der bekannte Zusammenhang zwischen der Höhenänderung und der Änderung des hydrostatischen Drucks in einem Fluid. Integration dieser Gleichung liefert die barometrische Höhenformel.

Chemisches Reaktionsgleichgewicht idealer Gase

Einführendes Beispiel

Als einführendes Beispiel[25] sei eine einfache chemische Gleichgewichtsreaktion des Typs

\mathrm {A\rightleftharpoons B}

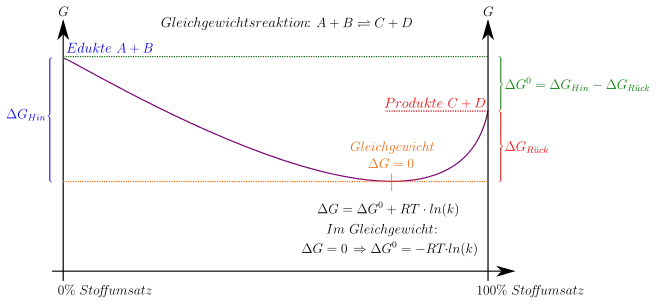
betrachtet, die bei konstanter Temperatur und konstantem Druck ablaufe. Das System bestehe anfangs aus reinem Ausgangsstoff $A$ , und es bilde sich daraus zunehmend das Produkt $B$ . Da es sich voraussetzungsgemäß um eine Gleichgewichtsreaktion handelt, findet gleichzeitig auch eine Rückumwandlung von $B$ nach $A$ statt (es könnte sich beispielsweise um eine Isomerisierung handeln, die in beide Richtungen ablaufen kann). Die Rückumwandlungsrate ist anfangs Null, da noch gar kein $B$ existiert. Je mehr $B$ jedoch durch die Hinreaktion $A\to B$ entstanden ist, desto größer wird auch die Rückumwandlungsrate. Bei einer bestimmten Zusammensetzung des chemischen Systems laufen Hin- und Rückreaktion mit derselben Umwandlungsrate ab, und die Zusammensetzung des Systems ändert sich nicht mehr – die Gleichgewichts-Zusammensetzung ist erreicht. Da sich ein solches System erfahrungsgemäß freiwillig in diesen Zustand begibt und der Prozess voraussetzungsgemäß unter isothermen und isobaren Bedingungen abläuft, ist die Gleichgewichts-Zusammensetzung dadurch gekennzeichnet, dass sie die Zusammensetzung mit der kleinsten Gibbs-Energie ist. Diese Tatsache erlaubt es, die zu erwartende Gleichgewichts-Zusammensetzung zu berechnen.

Der Reaktionsfortschritt beim Ablauf der Reaktion wird durch die Umsatzvariable $\xi$ gemessen. Im Anfangszustand hat $\xi$ den Wert Null. Wenn ein Mol in der Reaktion umgesetzt wurde, die Stoffmenge von $A$ also um ein Mol abgenommen und die Stoffmenge von $B$ um ein Mol zugenommen hat, dann hat $\xi$ den Wert 1 Mol erreicht, und so weiter.

Die Reaktion läuft laut Voraussetzung bei konstanter Temperatur und konstantem Druck ab, in der differentiellen Fundamentalfunktion $\mathrm {d} G$ (siehe oben)

\mathrm {d} G=-S\ \mathrm {d} T+V\ \mathrm {d} p+\mu _{A}\ \mathrm {d} n_{A}+\mu _{B}\ \mathrm {d} n_{B}

fallen also die von $\mathrm {d} T$ und $\mathrm {d} p$ abhängigen Terme fort und für die Änderung $\mathrm {d} G$ von $G$ bleiben unter diesen Bedingungen nur die Terme

{\begin{aligned}(\mathrm {d} G)_{T,p}&=\mu _{A}\ \mathrm {d} n_{A}+\mu _{B}\ \mathrm {d} n_{B}\\&=-\mu _{A}\ \mathrm {d} \xi +\mu _{B}\ \mathrm {d} \xi \end{aligned}}

Umstellen liefert die Gleichung

\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\mu _{B}-\mu _{A}

.

Diese Gleichung gibt für eine gegebene Mischung von $A$ und $B$ Auskunft darüber, in welcher Reaktionsrichtung die Gibbs-Energie abnimmt, in welche Richtung das System also von der vorliegenden Mischung ausgehend freiwillig läuft. Ausschlaggebend hierfür sind die chemischen Potentiale $\mu _{A}$ und $\mu _{B}$ . Im Fall $\mu _{B}<\mu _{A}$ ist die rechte Seite negativ, $G$ nimmt in positiver Reaktionsrichtung ab, die Reaktion läuft also in Richtung $B$ ; im Fall $\mu _{B}>\mu _{A}$ läuft sie in Richtung $A$ . Im Zuge des Reaktionsverlaufs ändern sich auch die von der Mischung abhängigen chemischen Potentiale, und sobald $\mu _{A}=\mu _{B}$ wird,[Anm. 15] ist auch $\mathrm {d} G=0$ . Die Gibbs-Energie ist im Minimum angekommen und das System hat sein Gleichgewicht erreicht, in dem sich seine Zusammensetzung nicht mehr ändert. Die allgemeine thermodynamische Gleichgewichtsbedingung für ein solches chemisches System lautet also einfach

0=\mu _{B}-\mu _{A}

oder

\mu _{B}=\mu _{A}

.

Hier zeigt sich auch der Grund für die Benennung „chemisches Potential“: Das chemische System strebt einen „Potentialausgleich“ an und hat das Gleichgewicht erreicht, wenn die beiden chemischen Potentiale gleich geworden sind.

Handelt es sich bei den reagierenden Substanzen insbesondere um ideale Gase, können die oben abgeleiteten Ausdrücke für deren chemische Potentiale in Abhängigkeit von den Partialdrücken $p_{A}$ und $p_{B}$ eingesetzt werden:

{\begin{aligned}\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}&=\mu _{B}-\mu _{A}\\&=\mu _{B}^{\circ }+RT\ \ln \left({\frac {p_{B}}{p^{\circ }}}\right)-\mu _{A}^{\circ }-RT\ \ln \left({\frac {p_{A}}{p^{\circ }}}\right)\\&=\mu _{B}^{\circ }-\mu _{A}^{\circ }+RT\ \ln \left({\frac {p_{B}}{p_{A}}}\right)\end{aligned}}

.

Die Ableitung $\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}$ auf der linken Seite beschreibt die Änderung der Gibbs-Energie pro Mol Formelumsatz bei der vorliegenden Zusammensetzung der reagierenden Mischung. Sie wird auch kurz als Gibbssche Reaktionsenergie $\Delta _{r}G$ bezeichnet.

Das chemische Potential $\mu _{A}^{\circ }$ bezieht sich auf den Standardzustand und daher auf die reine Substanz $A$ . Für diesen Fall ist aber, wie oben beschrieben, das chemische Potential identisch mit der molaren Gibbs-Energie. Die Differenz $\mu _{B}^{\circ }-\mu _{A}^{\circ }$ ist also gleich der Differenz $G_{m,B}^{\circ }-G_{m,A}^{\circ }$ der molaren Gibbs-Energien der im Standardzustand befindlichen reinen Substanzen $A$ und $B$ . Diese Differenz wird auch als molare Gibbssche Standardreaktionsenergie $\Delta _{r}G^{\circ }$ bezeichnet.

Die Gleichung lässt sich mit diesen Definitionen kürzer schreiben als

\Delta _{r}G=\Delta _{r}G^{\circ }+RT\ \ln \left({\frac {p_{B}}{p_{A}}}\right)

.

Im Gleichgewicht ist $\Delta _{r}G=0$ , also

-{\frac {\Delta _{r}G^{\circ }}{RT}}=\ln \left({\frac {p_{B}}{p_{A}}}\right)

oder

{\frac {p_{B}}{p_{A}}}=e^{-{\frac {\Delta _{r}G^{\circ }}{RT}}}=:K

Während die Einzelwerte $p_{A}$ und $p_{B}$ von den vorhandenen Anfangsmengen mitbestimmt werden und für verschieden angesetzte Experimente im Gleichgewicht unterschiedliche Werte annehmen können, ist ihr Verhältnis im Gleichgewichtszustand allein durch $\Delta _{r}G^{\circ }$ und die Temperatur bestimmt. Es ist für gegebene Substanzen $A$ und $B$ sowie gegebene Temperatur also eine Konstante, die Gleichgewichtskonstante $K$ . Das Gleichgewicht ist erreicht, sobald das Verhältnis der Partialdrücke diesen Zahlenwert angenommen hat.

Allgemeiner Fall

Änderung der Gibbs-Energie während einer Gleichgewichtsreaktion. Der vollständige Umsatz der Edukte wird nicht erreicht, da es stets eine Rückreaktion der Produkte gibt.

Im allgemeinen Fall[26] einer Reaktion mit komplexerer Stöchiometrie, die durch

a\ A+b\ B+\dots \,=\,p\ P+q\ Q+\dots

symbolisiert sei, stellt man die Reaktionsgleichung wie bei der Umformung einer mathematischen Gleichung so um, dass alle Summanden auf der rechten Seite stehen und erhält eine Reaktionsgleichung der Form

0=\sum _{J}\nu _{J}\ J

.

Dabei hat die zur Substanz $J$ gehörige stöchiometrische Zahl $\nu _{J}$ negatives Vorzeichen für die Ausgangsstoffe auf der linken Seite der ursprünglichen Gleichung und positives Vorzeichen für die Produkte auf der rechten Seite.

Schreitet die Umsatzvariable $\xi$ um $\mathrm {d} \xi$ fort, dann ändert sich die Stoffmenge der Substanz $J$ gemäß ihrer stöchiometrischen Zahl um $\mathrm {d} n_{J}=\nu _{J}\ \mathrm {d} \xi$ [Anm. 16] und die Änderung der Gibbs-Energie im Zuge der isothermen und isobaren Reaktion beträgt

(\mathrm {d} G)_{T,p}=-S\ \mathrm {d} T+V\ \mathrm {d} p+\sum _{J}\mu _{J}\ \mathrm {d} n_{J}=\sum _{J}\mu _{J}\ \nu _{J}\ \mathrm {d} \xi

.

Umstellen ergibt

\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=\sum _{J}\nu _{J}\ \mu _{J}

.

Im Gleichgewichtszustand ist die linke Seite Null und die allgemeine thermodynamische Gleichgewichtsbedingung für eine Reaktion mit dieser Stöchiometrie lautet

0=\sum _{J}\nu _{J}\ \mu _{J}

.

Hier strebt das System also einen Ausgleich der mit den (teils positiven, teils negativen) stöchiometrischen Zahlen gewichteten chemischen Potentiale an.

Handelt es sich bei den reagierenden Substanzen insbesondere um ideale Gase, können wieder die bekannten Ausdrücke für deren chemische Potentiale eingesetzt werden. Es ergibt sich unter Verwendung der Definition für die Gibbssche Reaktionsenergie $\left({\frac {\partial G}{\partial \xi }}\right)_{T,p}=:\Delta _{r}G$ sowie der auf mehrere Summanden erweiterten Definition der molaren Gibbsschen Standardreaktionsenergie $\sum _{J}\nu _{J}\ \mu _{J}^{\circ }=:\Delta _{r}G^{\circ }$ :

{\begin{aligned}\Delta _{r}G&=\sum _{J}\nu _{J}\ \mu _{J}\\&=\sum _{J}\nu _{J}\left(\mu _{J}^{\circ }+RT\ \ln \left({\frac {p_{J}}{p^{\circ }}}\right)\right)\\&=\left(\sum _{J}\nu _{J}\ \mu _{J}^{\circ }\right)+RT\ \sum _{J}\nu _{J}\ \ln \left({\frac {p_{J}}{p^{\circ }}}\right)\\&=\Delta _{r}G^{\circ }+RT\ \sum _{J}\ln \left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}\\&=\Delta _{r}G^{\circ }+RT\ \ln \prod _{J}\left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}\end{aligned}}

Im Gleichgewichtszustand ist $\Delta _{r}G=0$ , also

-{\frac {\Delta _{r}G^{\circ }}{RT}}=\ln \prod _{J}\left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}

oder

\prod _{J}\left({\frac {p_{J}}{p^{\circ }}}\right)^{\nu _{J}}=e^{-{\frac {\Delta _{r}G^{\circ }}{RT}}}=:K

Liegt beispielsweise die Reaktion

2\ A+3\ B\rightleftharpoons C+2\ D

vor, dann sind die zugehörigen stöchiometrischen Zahlen $\nu _{A}=-2$ , $\nu _{B}=-3$ , $\nu _{C}=1$ und $\nu _{D}=2$ .

Die allgemeine thermodynamische Gleichgewichtsbedingung für beliebige Substanzen $A$ , $B$ , $C$ und $D$ lautet

0=-2\ \mu _{A}-3\ \mu _{B}+\mu _{C}+2\ \mu _{D}

.

Handelt es sich insbesondere um eine ideale Gasmischung, dann liefert Verwendung der Formeln für die chemischen Potentiale idealer Gase die molare Gibbssche Standardreaktionsenergie

\Delta _{r}G_{m}^{\circ }=-2\mu _{A}^{\circ }-3\ \mu _{B}^{\circ }+\mu _{C}^{\circ }+2\ \mu _{D}^{\circ }

und die Gleichgewichtskonstante

K=e^{-{\frac {\Delta _{r}G^{\circ }}{RT}}}

.

Für die Partialdrücke folgt die Gleichgewichtsbedingung

{\frac {\left({\frac {p_{C}}{p^{\circ }}}\right)\left({\frac {p_{D}}{p^{\circ }}}\right)^{2}}{\left({\frac {p_{A}}{p^{\circ }}}\right)^{2}\left({\frac {p_{B}}{p^{\circ }}}\right)^{3}}}=K

.

Auch hier hängen die sich einstellenden Zahlenwerte für $p_{A},\dots ,p_{D}$ unter anderem von den eingesetzten Anfangsmengen ab, aber der genannte Ausdruck für das Verhältnis der Partialdrücke ist allein durch $\Delta _{r}G_{m}^{\circ }$ sowie die Temperatur bestimmt, ist also für die Substanzen $A,\dots ,D$ und die gegebene Temperatur in einer Reaktion der gegebenen Stöchiometrie eine Konstante, die Gleichgewichtskonstante $K$ . Die Reaktion hat den Gleichgewichtszustand erreicht, sobald das Verhältnis der Partialdrücke die obige Gleichgewichtsbedingung erfüllt.

Zur Ermittlung der molaren Gibbsschen Standardreaktionsenergie $\Delta _{r}G_{m}^{\circ }$ werden nur die molaren Gibbs-Energien der beteiligten reinen Stoffe im Standardzustand benötigt, die einschlägigen Tabellenwerken entnommen werden können.

Elektrochemie

In der Elektrochemie (s. Elektrochemische Spannungsreihe) kann die geleistete Nutzarbeit einer freiwilligen Umwandlung von chemischen Stoffen (z. B. einer Brennstoffzelle) über folgende Beziehung bestimmt werden:

\Delta _{\mathrm {r} }G=-z\cdot F\cdot E

mit

$\Delta _{\mathrm {r} }G$ – molare freie Reaktionsenthalpie
$z$ – Anzahl der übertragenen Elektronen in der betrachteten Reaktion
$F$ – Faradaykonstante: 96485,3399(24) A s/mol
$E$ – Gleichgewichtszellspannung

Gibbs-Energie als Fundamentalfunktion

Betrachtet man ein System, dessen Eigenschaften durch die Zustandsgrößen Entropie $S$ , Volumen $V$ und Molzahlen $n_{1},\dots ,n_{r}$ der $r$ chemischen Komponenten gegeben sind, dann ist die innere Energie $U$ des Systems, ausgedrückt als Funktion der genannten Zustandsgrößen (nämlich aller extensiven Variablen des Systems),

U=U(S,V,n_{1},\dots ,n_{r})

eine Fundamentalfunktion des Systems. Sie beschreibt das System vollständig, es lassen sich alle thermodynamischen Eigenschaften des Systems aus ihr ableiten.[3]^:13

Oft sind diese Variablen jedoch für die praktische Arbeit ungünstig und man würde vorziehen, etwa die Temperatur oder den Druck in der Variablenliste zu haben. Im Gegensatz zur sonst üblichen Vorgehensweise darf ein Variablenwechsel im vorliegenden Fall jedoch nicht durch eine einfache Substitution geschehen, da sonst Information verloren geht. Soll beispielsweise die Entropie durch die Temperatur $T$ ersetzt werden, könnte $S$ aus den Funktionen $U(S,V,n_{i})$ und $T(S,V,n_{i})$ eliminiert werden, um eine Funktion der Form $U(T,V,n_{i})$ zu erhalten. Da jedoch die Temperatur thermodynamisch als partielle Ableitung der inneren Energie nach der Entropie definiert ist

T=\left({\frac {\partial U}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}

wäre diese Formulierung gleichbedeutend mit einer partiellen Differentialgleichung für $U$ , welche $U$ nur bis auf unbestimmte Funktionen festlegen würde. Dieses $U$ wäre nach wie vor eine Beschreibung des betrachteten Systems, aber es wäre keine vollständige Beschreibung und damit keine Fundamentalfunktion mehr.[3]^{:63ff., 137ff.}

Zum Variablenwechsel unter Erhaltung der vollständigen Information muss eine Legendre-Transformation durchgeführt werden. Soll beispielsweise zur Variablenliste $(T,p,n_{1},\dots ,n_{r})$ übergegangen werden, lautet die Transformation:[3]^:147

{\begin{aligned}G(T,p,n_{1},\dots ,n_{r})&:=U(S,V,n_{1},\dots ,n_{r})-\left({\frac {\partial U}{\partial S}}\right)_{V,n_{1},\dots ,n_{r}}\cdot S-\left({\frac {\partial U}{\partial V}}\right)_{S,n_{1},\dots ,n_{r}}\cdot V\\&=U-T\,S+p\,V\\&=H-T\,S\end{aligned}}

Die Legendre-Transformierte $G=H-T\ S$ wird Gibbs-Energie genannt. Sie ist wiederum eine Fundamentalfunktion,[3]^:147 wenn sie als Funktion der Variablen $(T,p,n_{1},\dots ,n_{r})$ – dies sind die natürlichen Variablen der Gibbs-Energie – gegeben ist. Sie kann auch in Abhängigkeit von anderen Variablen ausgedrückt werden, ist dann aber keine Fundamentalfunktion mehr.

Die Herkunft der Gibbs-Energie aus einer Legendre-Transformation erklärt die additiven Terme $-T\,S$ und $p\,V$ : Sie kompensieren den Informationsverlust, der sonst mit dem Variablenwechsel verbunden wäre.

Die folgende Tabelle zeigt an einigen Beispielen, wie sich andere thermodynamische Größen aus der Fundamentalfunktion „Gibbs-Energie“ ableiten lassen:[27]

Zustandsgleichungen:

s(T,p)=-\left({\frac {\partial g}{\partial T}}\right)_{p}

v(T,p)=\left({\frac {\partial g}{\partial p}}\right)_{T}

h(T,p)=g-T\left({\frac {\partial g}{\partial T}}\right)_{p}

Ableitungen der kalorischen Zustandsgleichungen:

c_{p}(T,p):=\left({\frac {\partial h}{\partial T}}\right)_{p}=-T\left({\frac {\partial ^{2}g}{\partial T^{2}}}\right)_{p}

\left({\frac {\partial h}{\partial p}}\right)_{T}=v-T\left({\frac {\partial v}{\partial T}}\right)_{p}

Ableitungen der Entropie:

\left({\frac {\partial s}{\partial T}}\right)_{p}={\frac {c_{p}(T,p)}{T}}

\left({\frac {\partial s}{\partial p}}\right)_{T}=-\left({\frac {\partial v}{\partial T}}\right)_{p}

Literatur

Ulrich Nickel: Lehrbuch der Thermodynamik. Eine anschauliche Einführung. 3., überarbeitete Auflage. PhysChem, Erlangen 2019, ISBN 978-3-937744-07-0.
Hans Rudolf Christen: Grundlagen der allgemeinen und anorganischen Chemie. 5. Auflage. Verlag Sauerländer, 1977, S. 291–313.
Handbook of Chemistry and Physics. CRC-Press, Florida 1981.

Weblinks

Wikibooks: Tabellensammlung Chemie/ Thermodynamische Daten – Lern- und Lehrmaterialien

Video: Berechnung von Gleichgewichten - wo liegt das Minimum der GIBBSsche Energie?. Jakob Günter Lauth (SciFox) 2013, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/15666.

Anmerkungen

Die folgende Argumentation setzt voraus, dass das System Wärme nur mit dem Wärmereservoir und Volumen (und damit Volumenänderungsarbeit) nur mit dem Volumenreservoir austauscht. Würde Materie über die Systemgrenze fließen, könnte sie zusätzliche Wärme transportieren und Arbeit leisten, was daher ausgeschlossen werden muss.
Soll die gesamte vom System geleistete Arbeit untersucht werden, also unter Einschluss der Volumenänderungsarbeit, bietet sich die Verwendung der Freien Energie anstelle der Gibbs-Energie an, denn bei einem isothermen reversiblen Prozess ist die Abnahme der Freien Energie zahlenmäßig gleich der abgegebenen Gesamtarbeit: $\mathrm {d} W'_{\mathrm {gesamt} }=-\mathrm {d} F$ .
Die spezifische Gibbs-Energie in einem Gravitationsfeld ist nichts anderes als das Potential des Gravitationsfeldes.
Bewegt sich ein Teilchen der Masse $m$ in einem Gravitationsfeld, dann ist die vom Teilchen geleistete Arbeit
$\mathrm {d} W_{N}={\vec {K}}\cdot {\vec {\mathrm {d} l}}\,=\,K\,\cos(\vartheta )\,\mathrm {d} l$
ein Beispiel für mechanische Nicht-Volumenarbeit. Dabei ist $K$ der Betrag des auf das Teilchen wirkenden Kraftvektors, $\mathrm {d} l$ die Länge des vom Teilchen im Kraftfeld zurückgelegten Weges und $\vartheta$ der Winkel zwischen Kraftvektor und Weg.
Der Einfachheit halber seien im Folgenden Temperatur und Druck konstant und die Arbeitsleistung reversibel. Für die Änderung der Gibbs-Energie des Teilchens gilt dann
$\mathrm {d} G=-\mathrm {d} W_{N}\,=\,-K\,\cos(\vartheta )\,\mathrm {d} l$ .
Für die spezifische (also auf die Masse bezogene) Gibbs-Energie ist
$\mathrm {d} g=-\mathrm {d} w_{N}\,=\,-k\,\cos(\vartheta )\,\mathrm {d} l$
und die Änderung der spezifischen Gibbs-Energie bei einer Bewegung des Teilchens von Punkt $A$ nach Punkt $B$ ist
$\Delta g\,=\,-\int _{A}^{B}k\,\cos(\vartheta )\,\mathrm {d} l$ .
Das negative Integral über die von einer Einheitsmasse verrichtete Arbeit ist aber das Potential des Kraftfeldes.
Ähnliche Zusammenhänge lassen sich auch zwischen der Gibbs-Energie und anderen (konservativen) Kraftfeldern aufstellen.
In der Wahl des Variablensatzes $S,V,n_{1},\dots ,n_{r}$ steckt implizit auch die Voraussetzung, dass das System als einzige Form von Arbeit nur Volumenänderungsarbeit leistet, denn bei diesem Variablensatz steht nur $\mathrm {d} V$ als „Arbeitskoordinate“ zur Verfügung, die den Verlauf der Arbeitsleistung beschreiben kann. Soll das System auch andere Formen von Arbeit $W_{N}$ leisten, folgt aus der im Abschnitt zur maximalen Nicht-Volumenarbeit gezeigten Herleitung des Ausdrucks für $\mathrm {d} G$ die erweiterte differentielle Fundamentalfunktion
$\mathrm {d} G(T,p,{\color {NavyBlue}\dots },n_{1},\dots ,n_{r})=-S\,\mathrm {d} T+V\mathrm {d} p\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} n_{i}+{\color {NavyBlue}\mathrm {d} W_{N}}$ ,
wobei die Variablenliste um geeignete Arbeitskoordinaten zur Beschreibung von $W_{N}$ zu erweitern ist.
Die übrigen Folgerungen im vorliegenden Abschnitt bleiben davon unberührt.
Das chemische Potential kann neben der Gibbs-Energie auch aus anderen thermodynamischen Potentialen abgeleitet werden. Es ergibt sich dann als Funktion der natürlichen Variablen des betreffenden thermodynamischen Potentials. So gilt also für die innere Energie $U$ , die Enthalpie $H$ , die freie Energie $F$ und die Gibbs-Energie $G$ :
$\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{S,V,n_{j\neq i}}=\mu _{i}(S,V,n_{1},\dots ,n_{r})$

$\left({\frac {\partial H(S,p,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{S,p,n_{j\neq i}}=\mu _{i}(S,p,n_{1},\dots ,n_{r})$

$\left({\frac {\partial F(T,V,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{T,V,n_{j\neq i}}=\mu _{i}(T,V,n_{1},\dots ,n_{r})$

$\left({\frac {\partial G(T,p,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}=\mu _{i}(T,p,n_{1},\dots ,n_{r})$
Dabei ist zusätzlich vorauszusetzen, dass die gelöste Substanz einen so geringen Dampfdruck hat, dass sie nicht wesentlich im Dampfraum über der Lösung vorhanden ist, da sonst der Dampf über der Lösung eine Mischung und damit – entgegen der Annahme – kein einkomponentiges ideales Gas mehr ist.
In einer Mischung ist die Gibbssche Gesamtenergie im Allgemeinen nicht die Summe der (mit den Stoffmengen gewichteten) molaren Gibbs-Energien der Komponenten im reinen Zustand, sondern die Summe der (mit den Stoffmengen gewichteten) partiellen molaren Gibbs-Energien, die je nach Ausmaß der Wechselwirkungen der Komponenten miteinander sehr komplizierte Funktionen der Temperatur, des Drucks und der vorhandenen Stoffmengenanteile sein können. Die im vorliegenden Fall betrachteten idealen Gase wechselwirken jedoch definitionsgemäß nicht miteinander, so dass die im vorhergehenden Abschnitt abgeleitete Formel für das chemische Potential eines reinen idealen Gases auch für die idealen Gase in einer Mischung verwendet werden kann.
Ähnlich wie es sich bei „idealen Gasen“ um idealisierte Gase mit besonders einfachem Verhalten handelt, sind „ideale Mischungen“ idealisierte Mischungen mit besonders einfachem Verhalten. Ideale Gase müssen nicht unbedingt dadurch definiert werden, dass sie dem idealen Gasgesetz gehorchen. Sie können alternativ auch dadurch definiert werden, dass ihr chemisches Potential durch die Formel
$\mu =\mu ^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)$
beschrieben wird – sie befolgen dann automatisch das ideale Gasgesetz. Entsprechend können ideale Mischungen dadurch definiert werden, dass die chemischen Potentiale aller ihrer Komponenten durch Formeln der Gestalt
$\mu _{i}=\mu _{i}^{*}+R\,T\,\ln x_{i}$
beschrieben werden – sie haben dann automatisch die der Idealität entsprechenden einfachen Eigenschaften. $\mu _{i}^{*}$ ist das chemische Potential der $i$ -ten Substanz im reinen Zustand. $x_{i}$ ist der Stoffmengenanteil, mit dem die $i$ -te Substanz in der Mischung vertreten ist. Man beachte, dass die Stoffmengenanteile stets kleiner als Eins sind, ihr Logarithmus und damit der gesamte Term $R\,T\,\ln x_{i}$ also negative Werte annimmt. Diese Formeln beschreiben daher wie erwartet, dass das chemische Potential einer Substanz in einer (idealen) Mischung kleiner ist als im reinen Zustand.
Der Begriff „osmotischer Druck“ im weiteren Sinn bezeichnet hydrostatische Druckunterschiede, die sich aufgrund osmotischer Effekte einstellen. Im engeren Sinne ist aber damit der spezielle Zahlenwert für $\Pi$ gemeint, der gemäß dem van-’t-Hoff’schen Gesetz die osmotischen Eigenschaften einer Lösung charakterisiert. Es ist dabei gleichgültig, ob und in welchem Ausmaß in der vorliegenden Situation die osmotischen Effekte tatsächlich zu einer hydrostatischen Druckdifferenz zwischen den Phasen führen. Falls das aufgrund der Osmose durch die Membran tretende Lösungsmittel ungehindert abfließen kann, tritt trotz des Vorliegens von Osmose kein hydrostatischer Druckunterschied auf. Falls das Lösungsmittel in ein geschlossenes Volumen fließt, steigt dort der hydrostatische Druck $p$ an, bis er den Zahlenwert des die Lösung charakterisierenden Kennwerts „osmotischer Druck $\Pi$ “ erreicht hat. Je nach Zu- und Abflussverhältnissen können sich auch hydrostatische Drücke zwischen diesen Extremen ergeben.
Der Kennwert „osmotischer Druck“ kann in ähnlicher Weise anstelle der Stoffmengenanteile der gelösten Stoffe zur Charakterisierung der Lösung dienen, wie die Taupunkttemperatur der Luft anstelle des Wasserdampf-Partialdrucks zur Charakterisierung der Luftfeuchte dienen kann (und in der Regel nicht mit der Lufttemperatur identisch ist).
Die Herleitung kann ebenso gut mit den molaren Größen geführt werden, in den resultierenden Gleichungen treten dann die molaren Entropien, Latent-Enthalpien und Volumina auf.
Außerdem ist vorauszusetzen, dass im Verlaufe des Prozesses keine Nicht-Volumenarbeit geleistet wird, da in der differentiellen Gibbs-Funktion sonst ein zusätzlicher Term $\mathrm {d} w_{N}$ auftreten würde.
Genau genommen ändert sich der Druck in der Flüssigkeit nicht nur um die von der externen Ursache aufgeprägte Druckänderung $\Delta p$ , sondern zusätzlich noch um die resultierende Erhöhung des Dampfdrucks, der ja auf die Flüssigkeit zurückwirkt. Der Beitrag der Dampfdruckerhöhung ist in der Regel jedoch klein gegen $\Delta p$ und wird vernachlässigt.
Weil sich gleichzeitig Luft im ursprünglich reinen Wasser löst, tritt zusätzlich wegen des Raoultschen Gesetzes eine Erniedrigung des Sättigungsdampfdrucks um 0,014 Pa ein.
Der Überstrich dient lediglich dazu, den Betrag der Schwerefeldstärke ${\overline {g}}$ von der spezifischen Gibbs-Energie $g$ zu unterscheiden.
Es muss eine Zusammensetzung der Mischung geben, für die $\mu _{A}=\mu _{B}$ wird, da es sich gemäß Voraussetzung ja um eine Reaktion handelt, die einen Gleichgewichtszustand anstrebt und schließlich erreicht.
Im einführenden Beispiel war $\nu _{A}=-1$ und $\nu _{B}=1$ , also $\mathrm {d} \xi =-\mathrm {d} n_{A}=\mathrm {d} n_{B}$ .

Einzelnachweise

J. K. Fink: Physical Chemistry in Depth. Springer, Berlin Heidelberg 2009, ISBN 978-3-642-01013-2, S. 84.
Eintrag zu Gibbs energy (function). In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.G02629 – Version: 2.0.2.
H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 115.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 107.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 114.
E. Keszei: Chemical Thermodynamics. Springer, Berlin / Heidelberg 2012, ISBN 978-3-642-19863-2.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 118f.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 119.
K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge 1981, ISBN 0-521-28150-4.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 119 (die dortigen 2864 kJ hier korrekt auf 2865 kJ gerundet).
N. E. Edlefsen, A. B. C. Anderson: Thermodynamics of soil moisture. Hilgardia Band 15, Nr. 2 (Februar 1943), 31-298, doi:10.3733/hilg.v15n02p031.
H.-J. Lange: Die Physik des Wetters und des Klimas. Dietrich Reimer Verlag, Berlin 2002, ISBN 3-496-02747-9, S. 28f.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 144f.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 131.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 132.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 132.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 171.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 176.
J.C. Kotz, P.M. Treichel, J.R. Townsend: Chemistry & Chemical Reactivity. Thomson Brooks/Cole, Belmont, CA, 2009, ISBN 978-0-495-38703-9, S. 635 eingeschränkte Vorschau in der Google-Buchsuche
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 160.
J.E. McDonald: Intermolecular Attractions and Saturation Vapor Pressure. Journal of the Atmospheric Sciences, Band 20 (März 1963), Nr. 2, doi:10.1175/1520-0469(1963)020<0178:IAASVP>2.0.CO;2
$\gamma =0{,}073\ \mathrm {N\,m^{-1}}$ , $V_{\mathrm {m,l} }=18\ \mathrm {cm^{3}\,mol^{-1}} =1{,}8\cdot 10^{-5}\ \mathrm {m^{3}\,mol^{-1}}$
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 161.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 220 ff.
P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 223 f.
H. D. Baehr: Thermodynamik. 12. Auflage. Springer, Berlin/ Heidelberg/ New York 2005, ISBN 3-540-23870-0, S. 140.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[geschlossen-5] Die folgende Argumentation setzt voraus, dass das System Wärme nur mit dem Wärmereservoir und Volumen (und damit Volumenänderungsarbeit) nur mit dem Volumenreservoir austauscht. Würde Materie über die Systemgrenze fließen, könnte sie zusätzliche Wärme transportieren und Arbeit leisten, was daher ausgeschlossen werden muss.

[Arbeit-9] Soll die gesamte vom System geleistete Arbeit untersucht werden, also unter Einschluss der Volumenänderungsarbeit, bietet sich die Verwendung der Freien Energie anstelle der Gibbs-Energie an, denn bei einem isothermen reversiblen Prozess ist die Abnahme der Freien Energie zahlenmäßig gleich der abgegebenen Gesamtarbeit: $\mathrm {d} W'_{\mathrm {gesamt} }=-\mathrm {d} F$ .

[Kraftfeld-11] Die spezifische Gibbs-Energie in einem Gravitationsfeld ist nichts anderes als das Potential des Gravitationsfeldes.
Bewegt sich ein Teilchen der Masse $m$ in einem Gravitationsfeld, dann ist die vom Teilchen geleistete Arbeit
$\mathrm {d} W_{N}={\vec {K}}\cdot {\vec {\mathrm {d} l}}\,=\,K\,\cos(\vartheta )\,\mathrm {d} l$
ein Beispiel für mechanische Nicht-Volumenarbeit. Dabei ist $K$ der Betrag des auf das Teilchen wirkenden Kraftvektors, $\mathrm {d} l$ die Länge des vom Teilchen im Kraftfeld zurückgelegten Weges und $\vartheta$ der Winkel zwischen Kraftvektor und Weg.
Der Einfachheit halber seien im Folgenden Temperatur und Druck konstant und die Arbeitsleistung reversibel. Für die Änderung der Gibbs-Energie des Teilchens gilt dann
$\mathrm {d} G=-\mathrm {d} W_{N}\,=\,-K\,\cos(\vartheta )\,\mathrm {d} l$ .
Für die spezifische (also auf die Masse bezogene) Gibbs-Energie ist
$\mathrm {d} g=-\mathrm {d} w_{N}\,=\,-k\,\cos(\vartheta )\,\mathrm {d} l$
und die Änderung der spezifischen Gibbs-Energie bei einer Bewegung des Teilchens von Punkt $A$ nach Punkt $B$ ist
$\Delta g\,=\,-\int _{A}^{B}k\,\cos(\vartheta )\,\mathrm {d} l$ .
Das negative Integral über die von einer Einheitsmasse verrichtete Arbeit ist aber das Potential des Kraftfeldes.
Ähnliche Zusammenhänge lassen sich auch zwischen der Gibbs-Energie und anderen (konservativen) Kraftfeldern aufstellen.

[Variablen-16] In der Wahl des Variablensatzes $S,V,n_{1},\dots ,n_{r}$ steckt implizit auch die Voraussetzung, dass das System als einzige Form von Arbeit nur Volumenänderungsarbeit leistet, denn bei diesem Variablensatz steht nur $\mathrm {d} V$ als „Arbeitskoordinate“ zur Verfügung, die den Verlauf der Arbeitsleistung beschreiben kann. Soll das System auch andere Formen von Arbeit $W_{N}$ leisten, folgt aus der im Abschnitt zur maximalen Nicht-Volumenarbeit gezeigten Herleitung des Ausdrucks für $\mathrm {d} G$ die erweiterte differentielle Fundamentalfunktion
$\mathrm {d} G(T,p,{\color {NavyBlue}\dots },n_{1},\dots ,n_{r})=-S\,\mathrm {d} T+V\mathrm {d} p\,+\,\sum _{i=1}^{r}\mu _{i}\,\mathrm {d} n_{i}+{\color {NavyBlue}\mathrm {d} W_{N}}$ ,
wobei die Variablenliste um geeignete Arbeitskoordinaten zur Beschreibung von $W_{N}$ zu erweitern ist.
Die übrigen Folgerungen im vorliegenden Abschnitt bleiben davon unberührt.

[chemPot-18] Das chemische Potential kann neben der Gibbs-Energie auch aus anderen thermodynamischen Potentialen abgeleitet werden. Es ergibt sich dann als Funktion der natürlichen Variablen des betreffenden thermodynamischen Potentials. So gilt also für die innere Energie $U$ , die Enthalpie $H$ , die freie Energie $F$ und die Gibbs-Energie $G$ :
$\left({\frac {\partial U(S,V,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{S,V,n_{j\neq i}}=\mu _{i}(S,V,n_{1},\dots ,n_{r})$

$\left({\frac {\partial H(S,p,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{S,p,n_{j\neq i}}=\mu _{i}(S,p,n_{1},\dots ,n_{r})$

$\left({\frac {\partial F(T,V,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{T,V,n_{j\neq i}}=\mu _{i}(T,V,n_{1},\dots ,n_{r})$

$\left({\frac {\partial G(T,p,n_{1},\dots ,n_{r})}{\partial n_{i}}}\right)_{T,p,n_{j\neq i}}=\mu _{i}(T,p,n_{1},\dots ,n_{r})$

[Loesung-23] Dabei ist zusätzlich vorauszusetzen, dass die gelöste Substanz einen so geringen Dampfdruck hat, dass sie nicht wesentlich im Dampfraum über der Lösung vorhanden ist, da sonst der Dampf über der Lösung eine Mischung und damit – entgegen der Annahme – kein einkomponentiges ideales Gas mehr ist.

[partiellmolar-24] In einer Mischung ist die Gibbssche Gesamtenergie im Allgemeinen nicht die Summe der (mit den Stoffmengen gewichteten) molaren Gibbs-Energien der Komponenten im reinen Zustand, sondern die Summe der (mit den Stoffmengen gewichteten) partiellen molaren Gibbs-Energien, die je nach Ausmaß der Wechselwirkungen der Komponenten miteinander sehr komplizierte Funktionen der Temperatur, des Drucks und der vorhandenen Stoffmengenanteile sein können. Die im vorliegenden Fall betrachteten idealen Gase wechselwirken jedoch definitionsgemäß nicht miteinander, so dass die im vorhergehenden Abschnitt abgeleitete Formel für das chemische Potential eines reinen idealen Gases auch für die idealen Gase in einer Mischung verwendet werden kann.

[idealeMischung-28] Ähnlich wie es sich bei „idealen Gasen“ um idealisierte Gase mit besonders einfachem Verhalten handelt, sind „ideale Mischungen“ idealisierte Mischungen mit besonders einfachem Verhalten. Ideale Gase müssen nicht unbedingt dadurch definiert werden, dass sie dem idealen Gasgesetz gehorchen. Sie können alternativ auch dadurch definiert werden, dass ihr chemisches Potential durch die Formel
$\mu =\mu ^{\circ }+R\,T\,\ln \left({\frac {p}{p^{\circ }}}\right)$
beschrieben wird – sie befolgen dann automatisch das ideale Gasgesetz. Entsprechend können ideale Mischungen dadurch definiert werden, dass die chemischen Potentiale aller ihrer Komponenten durch Formeln der Gestalt
$\mu _{i}=\mu _{i}^{*}+R\,T\,\ln x_{i}$
beschrieben werden – sie haben dann automatisch die der Idealität entsprechenden einfachen Eigenschaften. $\mu _{i}^{*}$ ist das chemische Potential der $i$ -ten Substanz im reinen Zustand. $x_{i}$ ist der Stoffmengenanteil, mit dem die $i$ -te Substanz in der Mischung vertreten ist. Man beachte, dass die Stoffmengenanteile stets kleiner als Eins sind, ihr Logarithmus und damit der gesamte Term $R\,T\,\ln x_{i}$ also negative Werte annimmt. Diese Formeln beschreiben daher wie erwartet, dass das chemische Potential einer Substanz in einer (idealen) Mischung kleiner ist als im reinen Zustand.

[OsmotischerDruck-29] Der Begriff „osmotischer Druck“ im weiteren Sinn bezeichnet hydrostatische Druckunterschiede, die sich aufgrund osmotischer Effekte einstellen. Im engeren Sinne ist aber damit der spezielle Zahlenwert für $\Pi$ gemeint, der gemäß dem van-’t-Hoff’schen Gesetz die osmotischen Eigenschaften einer Lösung charakterisiert. Es ist dabei gleichgültig, ob und in welchem Ausmaß in der vorliegenden Situation die osmotischen Effekte tatsächlich zu einer hydrostatischen Druckdifferenz zwischen den Phasen führen. Falls das aufgrund der Osmose durch die Membran tretende Lösungsmittel ungehindert abfließen kann, tritt trotz des Vorliegens von Osmose kein hydrostatischer Druckunterschied auf. Falls das Lösungsmittel in ein geschlossenes Volumen fließt, steigt dort der hydrostatische Druck $p$ an, bis er den Zahlenwert des die Lösung charakterisierenden Kennwerts „osmotischer Druck $\Pi$ “ erreicht hat. Je nach Zu- und Abflussverhältnissen können sich auch hydrostatische Drücke zwischen diesen Extremen ergeben.
Der Kennwert „osmotischer Druck“ kann in ähnlicher Weise anstelle der Stoffmengenanteile der gelösten Stoffe zur Charakterisierung der Lösung dienen, wie die Taupunkttemperatur der Luft anstelle des Wasserdampf-Partialdrucks zur Charakterisierung der Luftfeuchte dienen kann (und in der Regel nicht mit der Lufttemperatur identisch ist).

[spezifisch-30] Die Herleitung kann ebenso gut mit den molaren Größen geführt werden, in den resultierenden Gleichungen treten dann die molaren Entropien, Latent-Enthalpien und Volumina auf.

[ClauClap-31] Außerdem ist vorauszusetzen, dass im Verlaufe des Prozesses keine Nicht-Volumenarbeit geleistet wird, da in der differentiellen Gibbs-Funktion sonst ein zusätzlicher Term $\mathrm {d} w_{N}$ auftreten würde.

[Delta_p-32] Genau genommen ändert sich der Druck in der Flüssigkeit nicht nur um die von der externen Ursache aufgeprägte Druckänderung $\Delta p$ , sondern zusätzlich noch um die resultierende Erhöhung des Dampfdrucks, der ja auf die Flüssigkeit zurückwirkt. Der Beitrag der Dampfdruckerhöhung ist in der Regel jedoch klein gegen $\Delta p$ und wird vernachlässigt.

[Raoult-35] Weil sich gleichzeitig Luft im ursprünglich reinen Wasser löst, tritt zusätzlich wegen des Raoultschen Gesetzes eine Erniedrigung des Sättigungsdampfdrucks um 0,014 Pa ein.

[overline-38] Der Überstrich dient lediglich dazu, den Betrag der Schwerefeldstärke ${\overline {g}}$ von der spezifischen Gibbs-Energie $g$ zu unterscheiden.

[muA=muB-40] Es muss eine Zusammensetzung der Mischung geben, für die $\mu _{A}=\mu _{B}$ wird, da es sich gemäß Voraussetzung ja um eine Reaktion handelt, die einen Gleichgewichtszustand anstrebt und schließlich erreicht.

[dnJ-42] Im einführenden Beispiel war $\nu _{A}=-1$ und $\nu _{B}=1$ , also $\mathrm {d} \xi =-\mathrm {d} n_{A}=\mathrm {d} n_{B}$ .

[Fink_84-1] J. K. Fink: Physical Chemistry in Depth. Springer, Berlin Heidelberg 2009, ISBN 978-3-642-01013-2, S. 84.

[2] Eintrag zu Gibbs energy (function). In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi:10.1351/goldbook.G02629 – Version: 2.0.2.

[Callen_1985-3] H. B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8.

[Atkins_115-4] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 115.

[6] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 107.

[7] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 114.

[Keszei_2012-8] E. Keszei: Chemical Thermodynamics. Springer, Berlin / Heidelberg 2012, ISBN 978-3-642-19863-2.

[10] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 118f.

[12] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 119.

[Denbigh_1981-13] K. Denbigh: The Principles of Chemical Equilibrium. 4th ed., Cambridge University Press, Cambridge 1981, ISBN 0-521-28150-4.

[14] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 119 (die dortigen 2864 kJ hier korrekt auf 2865 kJ gerundet).

[Edlefsen_1943-15] N. E. Edlefsen, A. B. C. Anderson: Thermodynamics of soil moisture. Hilgardia Band 15, Nr. 2 (Februar 1943), 31-298, doi:10.3733/hilg.v15n02p031.

[HJLange_28f-17] H.-J. Lange: Die Physik des Wetters und des Klimas. Dietrich Reimer Verlag, Berlin 2002, ISBN 3-496-02747-9, S. 28f.

[Atkins_144f-19] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 144f.

[20] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 131.

[21] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 132.

[22] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 132.

[25] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 171.

[26] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 176.

[27] J.C. Kotz, P.M. Treichel, J.R. Townsend: Chemistry & Chemical Reactivity. Thomson Brooks/Cole, Belmont, CA, 2009, ISBN 978-0-495-38703-9, S. 635 eingeschränkte Vorschau in der Google-Buchsuche

[Atkins_160-33] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 160.

[34] J.E. McDonald: Intermolecular Attractions and Saturation Vapor Pressure. Journal of the Atmospheric Sciences, Band 20 (März 1963), Nr. 2, doi:10.1175/1520-0469(1963)020<0178:IAASVP>2.0.CO;2

[36] $\gamma =0{,}073\ \mathrm {N\,m^{-1}}$ , $V_{\mathrm {m,l} }=18\ \mathrm {cm^{3}\,mol^{-1}} =1{,}8\cdot 10^{-5}\ \mathrm {m^{3}\,mol^{-1}}$

[37] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 161.

[39] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 220 ff.

[41] P. W. Atkins: Physikalische Chemie. 2. Nachdr. d. 1. Auflage. VCH, Weinheim 1990, ISBN 3-527-25913-9, S. 223 f.

[43] H. D. Baehr: Thermodynamik. 12. Auflage. Springer, Berlin/ Heidelberg/ New York 2005, ISBN 3-540-23870-0, S. 140.