Ionenradius
Der Ionenradius bezeichnet die effektive Größe eines einatomigen Ions in einem Ionengitter. Dabei wird vereinfachend angenommen, dass es sich um starre Kugeln handelt, deren Radien unabhängig vom Partner in der Ionenverbindung sind (sofern die Koordinationszahl gleich bleibt).
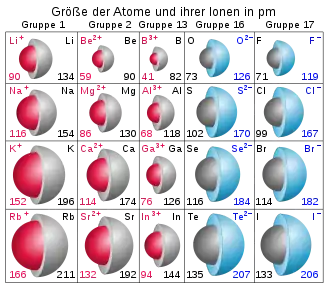
Um die Ionenradien zu ermitteln, bestimmt man zunächst die Abstände der im Kristallgitter auftretenden Ionen. Aus diesen Kationen-Anionen-Abständen erhält man zunächst die Radiensumme für verschiedene Ionenkombinationen. Damit die Radien der einzelnen Ionen bestimmt werden können, muss der Radius wenigstens eines beteiligten Ions unabhängig bekannt sein.
Pauling hat den Wert von 140 pm für ein O2−-Ion theoretisch bestimmt; dieser und die damit ermittelten weiteren Ionenradien gelten für die Koordinationszahl 6.
| Ion | Ionenradius in pm[2] |
|---|---|
| H− | 154 |
| F− | 133 |
| Cl− | 181 |
| O2− | 140 |
| S2− | 184 |
| Li+ | 76 |
| Na+ | 102 |
| K+ | 138 |
| NH4+ | 143 |
| Cu+ | 77 |
| Ag+ | 115 |
| Au+ | 137 |
Abhängigkeiten
Von Atomradius und Ladung
Ionenradien stehen mit Atomradien und Ladungen in folgendem Zusammenhang:
- bei Kationen, also positiv geladenen Ionen, ist der Ionenradius kleiner als der Atomradius. Je größer die positive Ladung, desto kleiner der Ionenradius.
- bei Anionen, also negativ geladenen Ionen, ist der Ionenradius größer als der Atomradius. Je größer die negative Ladung, desto größer der Ionenradius.
Kationen sind daher immer kleiner als die Anionen derselben Periode. Einige Kationen (K+, Rb+, Cs+, NH4+, Ba2+) sind jedoch größer als das insgesamt kleinste Anion F−.
Von der Stellung im Periodensystem
- Innerhalb einer Gruppe (d. h. im Periodensystem von oben nach unten) steigen die Ionenradien, da in jeder Periode ein neues Atomorbital vorhanden ist und so der Abstand der Valenzelektronen zum Atomkern zunimmt.
- Innerhalb einer Periode (d. h. im Periodensystem von links nach rechts) sinkt der Ionenradius (aber nur innerhalb der Kationen und dann wieder innerhalb der größeren Anionen, vgl. o. g. Abhängigkeit von der Ladung), da die Kernladungszahl (= Protonenzahl) steigt und so die Anziehungskraft des Atomkerns auf die Valenzelektronen größer wird.
Für Ionen der Übergangsmetalle hängt der Radius außerdem vom Spin-Zustand ab (Ligandenfeldtheorie).
Von der Koordinationszahl
Die Ionenradien stehen immer im direkten Zusammenhang mit der Koordinationszahl, d. h. mit der Anzahl der benachbarten Ionen: erhöht sich diese, so erhöhen sich auch die Abstoßungskräfte zwischen den Elektronenhüllen der Ionen, als Folge hieraus nimmt der Gleichgewichtsabstand zu.
Aus experimentell bestimmten Ionenradien ergibt sich, dass die relativen Änderungen der einzelnen Ionen individuell sind und man nur eine mittlere Näherung angeben kann:[3]
| Koordinationszahl | 8 | 6 | 4 |
|---|---|---|---|
| Ionenradius | 1,1 | 1,0 | 0,8 |
Die Tabelle zeigt, dass sich die Ionenradien von ein und demselben Ion verhalten wie 1,1:1,0:0,8 für die Koordinationszahlen 8, 6, 4. Daraus lässt sich schlussfolgern, dass sich die Ionenradien aus dem Gleichgewichtsabstand in einem Kristall ergeben und das Bild einer starren Kugel für ein isoliertes Ion nicht zutrifft.
Ein Ion verhält sich in verschiedenen Verbindungen also nur dann als starre Kugel mit annähernd konstantem Radius, wenn sich die Koordinationszahl nicht verändert.
Das Verhältnis der Ionenradien von Kationen/Anionen bestimmt, von wie vielen anderen Ionen sie jeweils umgeben sind (Koordinationszahl), und damit u. a. auch die Kristallstruktur bzw. den Kristallstrukturtyp.
Siehe auch
Literatur
- Erwin Riedel: Anorganische Chemie. de Gruyter, Berlin 2004, ISBN 3-11-018168-1.
- Erwin Riedel, Christoph Janiak: Anorganische Chemie. 7. Auflage. de Gruyter, Berlin 2007, ISBN 978-3-11-018903-2.
Einzelnachweise
- R. D. Shannon: Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. In: Acta Cryst. A32, 1976, S. 751–767, doi:10.1107/S0567739476001551 (englisch).
- Erwin Riedel, Christoph Janiak: Anorganische Chemie. 7. Auflage. de Gruyter, Berlin 2007, ISBN 978-3-11-018903-2, S. 75.
- Erwin Riedel, Christoph Janiak: Anorganische Chemie. 7. Auflage. de Gruyter, Berlin 2007, ISBN 978-3-11-018903-2, S. 74.