Gruppenbeitragsmethoden
Gruppenbeitragsmethoden (auch Fragmentmethoden oder Inkrementenmethoden) sind ein in der Technischen Chemie weit verbreitetes Verfahren zur Abschätzung von Stoffdaten.
Verfahren
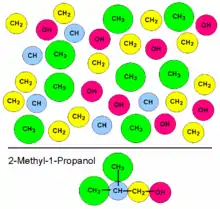
Chemische Eigenschaften, die etwa in der Prozesssimulation benötigt werden, sind immer Eigenschaften eines Stoffes oder einer Mischung von Stoffen. Da es eine nahezu unendliche und exponentiell weiter ansteigende Anzahl reiner Stoffe und Mischungen gibt, sind Gruppenbeitragsmethoden entwickelt worden, die Stoffeigenschaften nicht mehr den ganzen Stoffen zuordnen, sondern Fragmenten.
Der erzielte Effekt ist, dass aus wenigen Gruppeneigenschaften, typischerweise ein Dutzend bis wenige Hundert, die Stoffdaten für viele tausend Substanzen und deren Mischungen bestimmt werden können.
Diese Fragmente (die Gruppen) sind im Allgemeinen die funktionellen Gruppen eines Moleküls, wie etwa die Hydroxygruppe (-OH), die Aminogruppe (-NH2) oder die Carboxygruppe (-COOH). Häufig werden als Gruppen auch andere Molekülmerkmale hinzugenommen, wie etwa ortho-/meta-/para-Stellungen an Aromaten, Ringgrößen und Kettenlängen.
Reinstoffeigenschaften
Die gesuchte Eigenschaft wird als Funktion der Summe der Gruppenbeiträge errechnet:
Einige Ansätze zur Abschätzung von Reinstoffgrößen werden direkt über die Summe der Gruppenbeiträge abgeschätzt. Vielfach beschreibt die Summe der Gruppenbeiträge jedoch nicht die gesuchte Stoffgröße, sondern nur eine Rechengröße mit der die gesuchte Stoffgröße korreliert wird. Zusätzlich erfolgt darüber hinaus häufig auch noch eine Korrelation mit anderen Stoffgrößen. So wird beispielsweise bei der Berechnung der kritischen Temperatur in der Regel zusätzlich die Normalsiedetemperatur als weiterer Inputparameter verwendet: (Korrelationsgleichung nach Joback und Reid)
Gemischeigenschaften
Bei Modellen, die Eigenschaften von Mischungen abschätzen, werden häufig nicht allein die Summen der Gruppenbeiträge verwendet, sondern Gruppenwechselwirkungsparameter und verwendet.
Eine Eigenschaft, die typischerweise durch Gruppenwechselwirkungsmodelle wie UNIFAC oder ASOG berechnet wird, ist der Aktivitätskoeffizient .
Eine negative Auswirkung der Verwendung von Gruppenwechselwirkungen ist die massive Erhöhung der benötigten Parameter. Für 10 Gruppen werden bspw. bereits Wechselwirkungsparameter benötigt. Daher sind Gruppenwechselwirkungsmodelle zumeist nicht vollständig parametrisiert.
Bestimmung der Gruppenbeiträge
Die Gruppenbeiträge werden üblicherweise direkt an experimentell ermittelte Stoffdaten mittels multilinearer oder nichtlinearer Regression angepasst. Nichtlineare Regressionen stellen in aller Regel multimodale Optimierungsprobleme dar, also Optimierungsprobleme mit mehr als einem Optimum im betrachteten Lösungsraum. Zur Anpassung von Gruppenwechselwirkungsparametern werden daher oftmals Evolutionäre Algorithmen (z. B. (verschachtelte) Evolutionsstrategien, Genetische Algorithmen etc.) eingesetzt, da deterministische Optimierungsalgorithmen in der Regel nicht in der Lage sind, das globale Optimum (bei Regressionen: Minimum) zu finden.
Als Datenbasis experimentell ermittelter Stoffdaten dienen z. B. Faktendatenbanken wie Beilstein, die Dortmunder Datenbank oder die DIPPR 801-Datenbank. Oftmals werden auch zur Ergänzung experimentelle Messungen durchgeführt, wenn es Lücken in der betrachteten Gruppenwechselwirkungsmatrix gibt oder Gruppenbeitragsmethoden zusätzlich eine Temperatur- und/oder Druckabhängigkeit beschreiben.
Einschätzung der Genauigkeit
Die Vorhersagegenauigkeit einer Gruppenbeitragsmethode wird durch zwei Faktoren beeinflusst: Die Genauigkeit der Wiedergabe der experimentellen Daten durch die Gruppenbeitragsmethode und die Genauigkeit der zugrunde liegenden experimentellen Daten.
Beim Test der Güte einer Vorhersage wird in der Regel nur die Differenz zwischen Vorhersage und experimentellen Daten berücksichtigt. Entscheidend ist dabei, dass der Abgleich auch mit externen Daten erfolgt. Bei vielen Gruppenbeitragsmethoden (wie beispielsweise der Joback-Methode) wird in den entsprechenden Veröffentlichungen nur die Genauigkeit der Wiedergabe der experimentellen Daten angegeben, die für die Methodenentwicklung verwendet wurden. Das Problem hierbei ist, dass die Parameter der Methode (z. B. die Gruppenbeiträge) an genau diese Daten angepasst wurden. Sie wurden also für genau diesen Datensatz optimiert. Die erhaltenen Fehler der Vorhersage spiegeln daher oft nicht die tatsächliche Genauigkeit wider.
Um eine belastbare Aussage über Genauigkeit und Verlässlichkeit der Vorhersage treffen zu können, ist daher eine externe Validierung nötig. Dazu wird in der Regel vor Beginn der Methodenentwicklung ein Teil der verfügbaren experimentellen Daten (das so genannte Test Set) aus der Datenbasis entfernt. Mit Hilfe der verbliebenen Daten (dem so genannten Training Set) erfolgt dann die Entwicklung der Methode und die Anpassung der Parameter. Im Anschluss daran wird die Methode auf die Stoffe des Test Set angewendet und der entsprechende Fehler berechnet. Nur ein Fehler, der für ein Test Set ermittelt wurde, sollte als Genauigkeit einer Gruppenbeitragsmethode (oder analog eines QSPR-Modells) angesehen werden. Andernfalls muss die Genauigkeit der Vorhersage als unbekannt angesehen werden.[1]
Literatur
- Bruce E. Poling, John M. Prausnitz, John P. O’Connell, „The Properties of Gases and Liquids“, McGraw-Hill Publishing Co., 5th Edition.
- Jürgen Gmehling, Bärbel Kolbe, „Thermodynamik“, Georg-Thieme-Verlag, 1988.
- Peter Ulbig, Gruppenbeitragsmodelle UNIVAP & EBGCM, Gelsenkirchen, 1996, ISBN 3-920088-70-0.
- Hannes Geyer, Entwicklung und Untersuchung von Gruppenbeitragsmethoden zur Vorhersage thermodynamischer Stoffgrößen unter Verwendung von Methoden der Computational Intelligence, Shaker, Aachen, 2000, ISBN 3-8265-7000-6.
Siehe auch
Einzelnachweise
- A. Tropscha, P. Gramatica, V.J. Gombar: The Importance of Being Earnest: Validation is the Absolute Essential for Successful Application and Interpretation of QSPR Models. In: QSAR & Combinatorial Science. 22, Nr. 1, S. 69–77. doi:10.1002/qsar.200390007.