Zahl

Zahlen sind abstrakte mathematische Objekte beziehungsweise Objekte des Denkens, die sich historisch aus Vorstellungen von Größe und Anzahl entwickelten. Durch eine Messung wird ein als Größe verstandener Aspekt einer Beobachtung mit einer Zahl in Verbindung gebracht, beispielsweise bei einer Zählung. Sie spielen daher für die empirischen Wissenschaften eine zentrale Rolle.[1]

Übersicht über einige gängige Zahlbereiche.

A\subset B

bedeutet, dass die Elemente des Zahlbereiches

A

unter Beibehaltung wesentlicher Beziehungen auch als Elemente des Zahlbereichs

B

aufgefasst werden können. Echte Klassen sind in blau markiert.

In der Mathematik, die Zahlen und ihre Struktur formal untersucht, schließt der Begriff verschiedenartige Konzepte mit ein. Diese entwickelten sich als Verallgemeinerungen bestehender intuitiver Zahlkonzepte, so dass man sie ebenfalls als Zahlen bezeichnet, obwohl sie wenig Bezug zu den ursprünglich mit Messungen verbundenen Konzepten haben. Manche dieser Konzepte sind in der Mathematik von grundlegender Bedeutung und finden Verwendung in nahezu allen Teilgebieten.

In die Urgeschichte zurück reicht das Konzept der natürlichen Zahlen, die zum Zählen verwendet werden können und grundlegende Bedeutung besitzen. Bereits die Neandertaler schufen vor ca. 68.000 Jahren in Höhlen abstrakte Zahldarstellungen (zwei senkrechte Striche bzw. rot markierte Finger von Stalagmiten-Händen[2]). Ab etwa 2000 v. Chr. rechneten Ägypter und Babylonier mit Bruchzahlen (rationalen Zahlen). In Indien entwickelte sich im 7. Jh. n. Chr. ein Verständnis der Null und der negativen Zahlen.[3] Irrationale Zahlen wie ${\sqrt {2}}$ oder ${\sqrt {5}}$ , deren Notwendigkeit sich aus Erkenntnissen aus dem antiken Griechenland ergab (spätestens ab dem 4. Jh. v. Chr.), wurden in der Blütezeit des Islam eingeführt.

Die Idee imaginärer Zahlen, durch die die reellen Zahlen später zu den bedeutenden komplexen Zahlen erweitert wurden, reicht in die europäische Renaissance zurück. Der Begriff der reellen Zahl konnte erst im 19. Jahrhundert hinreichend geklärt werden. Ende des 19. Jh. konnte erstmals auch unendlichen Größen ein präziser Sinn als Zahlen gegeben werden. Auch wurden erstmals die natürlichen Zahlen axiomatisch definiert. Mit den Anfang des 20. Jh. geschaffenen ersten zufriedenstellenden Grundlagen der Mathematik erfuhren auch die bedeutendsten Zahlbegriffe eine dem heutigen Stand entsprechende vollständig formale Definition und Bedeutung.

Vom Begriff der Zahl abzugrenzen sind Ziffern (spezielle Zahlzeichen; zur Darstellung bestimmter Zahlen verwendete Schriftzeichen), Zahlschriften (Schreibweisen von Zahlen z. B. mit Hilfe von Ziffern unter Verwendung bestimmter Regeln), Zahlwörter (Numerale, zur Benennung bestimmter Zahlen verwendete Wörter) und Nummern (Identifikatoren, die selbst Zahlen, oder aber – in der Regel Ziffern enthaltende – Zeichenketten sein können).

Etymologie

Das deutsche Wort Zahl geht vermutlich auf das urgermanische Wort *talō (Berechnung, Zahl, Rede)[4][5] zurück, das vermutlich Wurzel der althochdeutschen Wörter zala (Ordnung, geordnete Darlegung, Bericht, Aufzählung)[6] und zalōn (berichten, rechnen, zählen,[6] berechnen, zahlen[7]) ist. Aus zala wurde im Mittelhochdeutschen zale oder zal,[6] auf das das heutige Wort Zahl zurückgeht.

Das urgermanische Wort findet seinen Ursprung vermutlich in einem urindogermanischen Etymon *del- (zielen, berechnen, nachstellen).[7][4] Auch ein Zusammenhang mit dem urindogermanischen *del- (spalten)[7] ist möglich; die ursprüngliche Bedeutung wäre dann möglicherweise „eingekerbtes Merkzeichen“.[8][9]

Geschichte

Vorgeschichte

Über das Zahlenverständnis von Menschen in der Zeit vor einer ersten schriftlichen Überlieferung lässt sich wegen fehlender Belege kaum Sicheres sagen. Die Bedeutung regelmäßiger Anordnungen von Strichen oder Kerben, die sich aus dieser Zeit erhalten haben, kann in der Regel nur vermutet werden.

Hinweise zur Vorstellung von Zahlen in einer vorgeschichtlichen Kultur können hingegen die jeweiligen Sprachen möglichst früher, geschichtlich dokumentierter Nachfolgerkulturen oder auch heute noch existierende, verwandte Sprachen sowie die bekannten Sprachen von alten, ähnlichen Kulturen geben. Durch systematische Vergleiche verschiedener Sprachen können Übereinstimmungen und Unterschiede zwischen diesen festgestellt werden, so dass die Eigenheiten jeder Sprache und Sprachgruppe ermittelt sowie gemeinsame oder verschiedene Herkünfte in gewissem Umfang gefunden werden können. So ergeben sich auch bei den Zahlwörtern Strukturen, die Rückschlüsse auf das Zahlenverständnis erlauben.[10]

Der fundamentale und überall in menschlichen Sprachen erkennbare Zahlbegriff – die Vorstellung von Zahlen – ist der von der unterschiedlich großen Anzahl bzw. Menge bestimmter Gegenstände, was am ehesten in der heutigen Mathematik dem Begriff der Kardinalzahl entspricht.[11] Am Anfang wird wohl der elementare Gegensatz von Einzahl und Mehrzahl gestanden haben, dem die weitere Aufteilung der Mehrzahl folgte.[12] In der Sprache der Pirahã in Brasilien etwa sind lediglich drei oder sogar nur zwei Wörter („wenig“ und „viel“) für relative Größenangaben bekannt.[13] Versuche, manchen Vertretern dieses Volkes das Zählen beizubringen, schlugen fehl.[14] Es gibt auch ethnologische Berichte über ein Volk in Südafrika und von vielen Völkern australischer Ureinwohner,[15] die in ihren Sprachen jeweils nur die Zahlwörter „ein“, „zwei“ und „viel“ kennen. Das Gleiche findet sich auch in indoeuropäischen Sprachen in Form des Singulars, des Duals (z. B. im Griechischen, im Latein und früher auch in germanischen Sprachen) und des Plurals von Substantiven wieder.[16][17]

Um „viel“ weiter unterscheiden und genauere Anzahlen sagen zu können, bildeten andere Völker weitere Zahlwörter.[18] Bis höchstens zehn (für größere Zahlen würden die Zahlwörter zu lang werden) ist dies einfach dadurch möglich, dass „zwei“ additiv so oft wiederholt wird, wie sie in der entsprechenden Zahl enthalten ist, und bei einer ungeraden Zahl wird noch ein „ein“ hinzugefügt. Einen anderen Weg, Wörter für größere Zahlen zu erhalten, haben Sprachen beschritten, die für kleinere Zahlen zusätzliche eigene Worte wie „drei“, „vier“ oder „fünf“ erfanden und diese wiederum additiv oder multiplikativ, z. B. „vier-zwei“ für acht,[19] zu neuen größeren Zahlen verbanden. Für die Bildung von wesentlich größeren Zahlen als zehn wird es notwendig, große Zahlen zu neuen, größeren Einheiten zusammenzufassen und für diese neue Zahlworte zu finden,[20] etwa in Stufen zu „zehn“, „hundert“ usw.

Auf diese Art lassen sich so große Zahlen bilden, dass es für deren genaue Erfassung erforderlich wird, eine entsprechende Anzahl von Gegenständen zu zählen. Dabei muss jedoch noch keine Trennung der Zahlen von der Art der gezählten Gegenstände vorliegen: bei manchen Sprachen gibt es so genannte Zählklassen, die für die gleiche Zahl jeweils ein eigenes Zahlwort haben.[21] So benutzt man für die gleiche Anzahl Lebewesen ein anderes Wort als bei langen Gegenständen, bei runden Gegenständen ein drittes Wort und bei noch anderen Gegenständen weitere Wörter.

Mit der Loslösung von der Art der Gegenstände, also wenn unabhängig von den gezählten Gegenständen das gleiche Zahlwort für die gleiche Anzahl benutzt wird, erhalten Zahlen Selbstständigkeit und werden als etwas Eigenes aufgefasst. Bei indoeuropäischen Sprachen ist dies allgemein für Zahlen größer als vier zu beobachten. Hier scheint es ursprünglich eine Stufung mit vier gegeben zu haben,[22] später wurden die Zahlen offenbar noch in mehreren Schritten erweitert (das erkennt man z. B. im Deutschen am Unterschied zwischen „dreizehn“ und „dreiundzwanzig“). Neben Zusammenfassungen von jeweils zwei, drei oder vier treten weltweit auch häufig noch Sprachen auf mit Stufen von fünf, zehn, zwölf oder zwanzig sowie mit Mischformen von diesen.[23][24]

Erste Hochkulturen

Fragment des Papyrus Rhind, pBM 10057

Der nach der letzten Kaltzeit (nach 10.000 v. Chr.)[25] in der Mittelsteinzeit einsetzende Klimawandel[26] führte zur Austrocknung großer Gebiete von der Sahara im Westen bis zur Mongolischen Steppe im Osten. Die zunehmende Bevölkerung der betroffenen Gebiete wanderte in die Flussoasen, wo sich mit der Zeit differenziertere städtische Gesellschaften entwickelten. Mit der Erfindung der Schrift bei den frühen Hochkulturen an Euphrat und Tigris (Mesopotamien), am Nil (Altes Ägypten), am Indus (Indus-Kultur) und am Gelben Fluss (Altes China) begann zwischen dem Ende des 4. und dem Anfang des 3. Jahrtausends v. Chr. die geschichtliche Zeit.[27][28] Von Beginn an entstanden zusammen mit der Schrift auch Zahlzeichen, da offenbar beides zur Verwaltung der immer stärker organisierten Gesellschaften benötigt wurde.

Im alten Ägypten fand spätestens seit ca. 3000 v. Chr. zur Darstellung natürlicher Zahlen ein additives Zahlensystem zur Basis 10 Verwendung.[29] Dort wurden bereits die Grundrechenarten der Addition, Subtraktion, Multiplikation und Division betrieben. Für die ersteren beiden gab es besondere Schriftzeichen.[30] Besonders bedeutsame Zeugnisse mathematischer Fähigkeiten dieser Kultur sind der Moskauer Papyrus und der Papyrus Rhind – beide in hieratischer Schrift verfasst in der Zeit zwischen 2000 v. Chr. und 1800 v. Chr. Aus diesem lässt sich über die natürlichen Zahlen hinausgehend eine besondere Notation für Stammbrüche entnehmen. Andere Verhältnisse wurden systematisch in Summen von Stammbrüchen überführt ( ${\tfrac {2}{3}}$ besaß jedoch auch ein eigenes Zeichen).[31] Motivation der altägyptischen Mathematik waren meist Bauwesen, Landvermessung und Wirtschaft, Beweise finden sich nicht.[32] Jedoch finden sich auch Probleme, die als humorvoll oder unterhaltsam intendiert interpretiert werden.[33][34][35]

Ebenfalls gibt es reichhaltige mathematische Zeugnisse aus dem Mesopotamien des Altertums. In sumerischer Zeit entwickelte sich dort ein additives Zahlensystem, basierend auf den Basen 10 und 60. Aus altbabylonischer Zeit zwischen 1.800 und 1.600 v. Chr. gibt es zahlreiche Funde mit weitergehenden Errungenschaften: Es entstand ein sexagesimales Stellenwertsystem, jedoch mit der Einschränkung, dass es keine Ziffer Null gab und die Notation daher uneindeutig war. Innerhalb dieses Systems wurden auch allgemeinere rationale Zahlen in einer der heute gebräuchlichen Dezimalbruchentwicklung entsprechenden Weise dargestellt, d. h., es konnten etwa ${\tfrac {1}{60}}$ - und ${\tfrac {1}{3600}}$ -Stellen gebraucht werden. Auf diese Weise nicht darstellbare Brüche oder (in moderner Sprechweise) Logarithmen, wie sie bei der Zinsrechnung auftraten, wurden näherungsweise dargestellt. In Gestalt des babylonischen Wurzelziehens wurden auch systematische Approximationen vorgenommen.[36] Zudem wurden Lösungen für quadratische, kubische und biquadratische Gleichungen gefunden. Diese Gleichungen wurden mit geometrischen Begriffen beschrieben (ein in moderner Sprechweise in solchen Gleichungen auftretendes Quadrat wurde als Flächeninhalt beschrieben, von dem etwa eine Seitenlänge subtrahiert wird, dass als Flächeninhalte und als Längen bezeichnete Größen addiert werden konnten, legt jedoch ein recht abstraktes, algebraisches Verständnis nahe).[37][38] Diese Errungenschaften entstammten praktischen Bedürfnissen von Wirtschaft, Bauwesen und Astronomie.[39]

Antikes Griechenland

Aus dem antiken Griechenland sind eine Vielzahl mathematischer Erkenntnisse überliefert. Erstmals (soweit bekannt) kam es hier zum ausgeprägten Verständnis von Beweisen,[40] durch die die Ergebnisse in einer der heutigen Mathematik nahekommenden Strenge bewiesen wurden. Besondere Bedeutung hatte ab dem 6. Jahrhundert v. Chr. die Schule der Pythagoreer, gegründet von Pythagoras von Samos (ca. 570–510 v. Chr.), der vermutlich durch Reisen nach Ägypten, Mesopotamien und evtl. Indien beeinflusst war.[41] In dieser religiösen Gruppierung trennte sich die Mathematik vom aus den Notwendigkeiten des Alltags entspringenden Rechnen,[42] wobei (natürliche) Zahlen eine zentrale Rolle spielten. Die Überlieferungslage bezüglich dieser Zeit der Mathematikgeschichte, den mutmaßlich etwas früher lebenden Thales von Milet mit eingeschlossen, ist allerdings noch dünn, die meisten Dokumente stammen aus späterer Zeit, so dass sich nicht sicher sagen lässt, welche Konzepte dort schon bekannt waren, und mit welcher Methodik verfahren wurde.[43]

Aus nicht vollständig geklärten Gründen legte die darauffolgende griechische Mathematik großen Wert auf die Geometrie, trotz des Einflusses der Pythagoreer, unter denen die Arithmetik als grundlegend aufgefasst worden war.[44] Bedeutende Protagonisten waren hier Eudoxos von Knidos (* zw. ca. 397 und 390 v. Chr., † zw. ca. 345 und 338 v. Chr.) und Euklid (ca. 360–280 v. Chr.).

Bezüglich des Zahlbegriffs der Griechen muss festgestellt werden, dass sie nicht über ein Konzept rationaler Zahlen als algebraische Objekte oder Erweiterung der natürlichen Zahlen verfügten. Die aus moderner Sicht oft als Aussagen über solche interpretierten Ergebnisse wurden geometrisch als Aussagen über Längen- und Flächenverhältnisse formuliert: Eine Länge oder Fläche konnte ein ganzzahliges Vielfaches einer anderen sein, dementsprechend lassen sich Verhältnisse zwischen zwei solchen Vielfachen einer Länge oder Fläche im heutigen Verständnis als (positive – mit negativen Zahlen vergleichbare Konzepte waren nicht vorhanden) rationale Zahlen beschreiben, im griechischen Verständnis von Zahlen waren sie jedoch nicht enthalten. Erst recht gab es keine irrationalen Zahlen in der griechischen Mathematik – es traten lediglich geometrische Verhältnisse auf, die keinem Verhältnis von zwei ganzzahligen Vielfachen einer Größe entsprachen; man spricht von Inkommensurabilität.[45][46] Selbst die Eins wurde bei Euklid nicht zu den Zahlen gezählt.[47][48]

Die Existenz der inkommensurablen Verhältnisse war spätestens seit Aristoteles (384–322 v. Chr.), der einen recht allgemeinen Beweis lieferte, womöglich aber schon vor 400 v. Chr.[49] in Griechenland bekannt. Dies zeigte die Unmöglichkeit des pythagoreischen Ansatzes, die in der Geometrie auftretenden Verhältnisse mittels der Arithmetik zu beschreiben – in heutiger Begrifflichkeit eine Unzulänglichkeit der rationalen Zahlen.[50] Der Übergang zu einer geometrischen Grundlegung, die den Umgang mit solchen Verhältnissen erlaubte, wird maßgeblich auf Eudoxos zurückgeführt, der selbst noch Schüler des bedeutenden Pythagoreers Archytas von Tarent gewesen war, der die Arithmetik als einzige mögliche Grundlage für Beweise ansah.[51]

Eudoxos lieferte eine Definition der Gleichheit zweier geometrischer Verhältnisse (von Längen oder Flächen): Zwei Verhältnisse sind demzufolge gleich, wenn alle – in moderner Interpretation – rationalen Verhältnisse, die kleiner bzw. größer sind als das eine Verhältnis, auch kleiner bzw. größer sind als das andere.[52] Diese Definition gilt sogar analog für den heutigen Begriff der reellen Zahlen. Einige Stimmen sahen oder sehen hierin bereits ein Vorhandensein der reellen Zahlen in der griechischen Mathematik.[53][54][55] Diese Aussagen sind jedoch problematisch:[55] Zum einen war eben nicht einmal das Konzept der rationalen Zahlen vorhanden, zum anderen wurde nichts darüber ausgesagt, dass bestimmte Verhältnisse existieren, so dass diese etwa ordnungsvollständig sind, sondern vielmehr durch die Geometrie gegebene Verhältnisse untersucht. In jedem Fall ermöglichte diese Definition eine Vielzahl von Beweisen, deren Techniken wie die Exhaustionsmethode als Vorläufer heutiger Begriffe der Analysis gelten, wobei gewisse Abschätzungen bereits eine zentrale Rolle spielten. Zudem war Richard Dedekind bei seiner Definition der reellen Zahlen eigenen Angaben zufolge durch Eudoxos inspiriert.[55]

Archimedes, ein Gemälde von Domenico Fetti aus dem Jahr 1620

Archimedes von Syrakus (287–212 v. Chr.), der aufbauend auf Eudoxos besonders weitreichende Beweise für bestimmte geometrische Verhältnisse sowie bestimmte Näherungen lieferte, gilt auch als erste Person, die infinitesimale Größen einführte: Im Archimedes-Palimpsest wandte er ein Prinzip vergleichbar dem Prinzip von Cavalieri an, bei dem eine Fläche in unendlich viele infinitesimale Linien zerlegt wird. Eine solche Vorgehensweise entsprach schon damals nicht den Ansprüchen an einen mathematischen Beweis, Archimedes sah in diesem mechanisch motivierten Verfahren jedoch ein nützliches Werkzeug, um an ein Problem heranzugehen und später einfacher einen korrekten Beweis finden zu können.[56] Die Existenz von von Null verschiedenen infinitesimalen Größen widerspricht der Definition des Eudoxos von Gleichheit und auch dem von Archimedes selbst aufgestellten sogenannten Archimedischen Axiom.

Definition von Zahlen

Der Begriff der Zahl ist nicht mathematisch definiert, sondern ein gemeinsprachlicher Oberbegriff für verschiedene mathematische Konzepte. Daher gibt es im mathematischen Sinn keine Menge aller Zahlen oder dergleichen. Die Mathematik spricht, wenn sie sich mit Zahlen befasst, stets über bestimmte wohldefinierte Zahlbereiche, d. h. nur über bestimmte Objekte unseres Denkens mit festgelegten Eigenschaften, die zusammenfassend alle als Zahlen bezeichnet werden. Seit dem Ende des 19. Jahrhunderts werden in der Mathematik Zahlen rein mittels der Logik unabhängig von Vorstellungen von Raum und Zeit definiert. Grundsteine wurden hier von Richard Dedekind und Giuseppe Peano mit der Axiomatisierung der natürlichen Zahlen (Siehe Peano-Axiome) gelegt. Dedekind schreibt zu diesem neuen Ansatz:

„Was beweisbar ist, soll in der Wissenschaft nicht ohne Beweis geglaubt werden. So einleuchtend diese Forderung erscheint, so ist sie doch, wie ich glaube, selbst bei der Begründung der einfachsten Wissenschaft, nämlich desjenigen Theiles der Logik, welcher die Lehre von den Zahlen behandelt, auch nach den neuesten Darstellungen noch keineswegs als erfüllt anzusehen. […] die Zahlen sind freie Schöpfungen des menschlichen Geistes, sie dienen als ein Mittel, um die Verschiedenheit der Dinge leichter und schärfer aufzufassen. Durch den rein logischen Aufbau der Zahlen-Wissenschaft und durch das in ihr gewonnene stetige Zahlen-Reich sind wir erst in den Stand gesetzt, unsere Vorstellungen von Raum und Zeit genau zu untersuchen, indem wir dieselben auf dieses in unserem Geiste geschaffene Zahlen-Reich beziehen.“

– Richard Dedekind: Was sind und was sollen die Zahlen? Vorwort zur ersten Auflage.[57]

Zu unterscheiden sind axiomatische Definitionen von mengentheoretischen Definitionen von Zahlen: Im ersteren Fall wird die Existenz gewisser Objekte mit auf ihnen definierten Verknüpfungen mit bestimmten Eigenschaften in Form von Axiomen postuliert, so etwa auch bei den frühen Axiomatisierungen der natürlichen und der reellen Zahlen durch Peano und Dedekind. In der Folge der Entwicklung der Mengenlehre durch Georg Cantor ging man dazu über, zu versuchen, sich auf mengentheoretische Axiome zu beschränken, wie es in der Mathematik heute etwa mit der Zermelo-Fraenkel-Mengenlehre (ZFC) üblich ist. Die Existenz gewisser Zahlenmengen und Verknüpfungen über ihnen mit gewissen Eigenschaften wird dann aus diesen Axiomen gefolgert. Mitunter wird ein Zahlbereich als eine bestimmte Klasse definiert. Die axiomatische Mengenlehre versucht, eine einzige, einheitliche formale Grundlage für die gesamte Mathematik zu sein. Innerhalb ihrer lässt sich auf reichhaltige Weise mit den Zahlbereichen umgehen. Formuliert wird sie in der Regel in der Prädikatenlogik erster Stufe, die die Struktur der mathematischen Sätze sowie die Möglichkeiten zur Schlussfolgerung aus den Axiomen festlegt.

Elementares Beispiel einer mengentheoretischen Definition einer Menge von Zahlen ist die von John von Neumann eingeführte Definition der natürlichen Zahlen als die kleinste induktive Menge, deren Existenz im Rahmen der Zermelo-Fraenkel-Mengenlehre durch das Unendlichkeitsaxiom postuliert wird.

Als mengentheoretische Konzepte werden Ordinal- und Kardinalzahlen in aller Regel mengentheoretisch definiert, ebenso die Verallgemeinerung der surrealen Zahlen.

Die Peano-Axiome etwa und die auf Dedekind zurückgehende Definition der reellen Zahlen basieren im Gegensatz zu ZFC auf der Prädikatenlogik zweiter Stufe. Während die Prädikatenlogik erster Stufe eine klare, allgemein akzeptierte Antwort darauf liefert, wie gültige Schlüsse vorzunehmen sind, wobei diese sich systematisch berechnen lassen, führen Versuche, dies für die Prädikatenlogik zweiter Stufe zu klären, meist dazu, dass eine komplexe Metatheorie eingeführt werden muss, die ihrerseits mengentheoretische Begriffe metasprachlich einführt und von deren Details die in der Folge erschlossenen Möglichkeiten der Folgerung in der Prädikatenlogik zweiter Stufe abhängen. ZFC ist ein Kandidat für eine solche Theorie.[58] Diese Einschränkungen lassen die Prädikatenlogik zweiter Stufe in einem Teil der Philosophie der Mathematik ungeeignet erscheinen, auf grundlegender Ebene verwendet zu werden.[59] Die Prädikatenlogik erster Stufe dagegen ist nicht hinreichend, um gewisse wichtige intuitive Eigenschaften der natürlichen Zahlen zu formulieren und (bei Betrachtung dieser in einer mengentheoretischen Metatheorie, etwa aufgrund des Satzes von Löwenheim-Skolem die Abzählbarkeit) sicherzustellen.

Verknüpfungen von Zahlen

Die Mathematik untersucht Beziehungen zwischen mathematischen Objekten und beweist strukturelle Eigenschaften in diesen Beziehungen. Elementare Beispiele für zwischen Zahlen definierte Beziehungen sind etwa die allgemein bekannten Rechenoperationen (Grundrechenarten) über den rationalen Zahlen (Brüche), Vergleiche („kleiner“, „größer“, „größer gleich“ etc.) zwischen rationalen Zahlen und die Teilbarkeitsrelation zwischen ganzen Zahlen („3 ist ein Teiler von 9“). Zudem werden Eigenschaften über bestimmten Zahlen definiert, zum Beispiel ist über den ganzen Zahlen die Eigenschaft definiert, eine Primzahl zu sein.

Solche Verknüpfungen sind nicht als vom Zahlbegriff unabhängige willkürliche Operationen zu verstehen, vielmehr werden bestimmte Zahlbereiche meist untrennbar von bestimmten Verknüpfungen betrachtet, da diese die zu untersuchende Struktur maßgeblich bestimmen. Spricht man etwa über die natürlichen Zahlen, gebraucht man fast immer zumindest auch ihre Ordnung („ $1<5$ “, „ $12<19$ “), welche maßgeblich unseren Begriff von natürlichen Zahlen bestimmt.

In der Schulmathematik, der Informatik und der numerischen Mathematik befasst man sich mit Verfahren, um solche Verknüpfungen auf konkreten Darstellungen von Zahlen auszuwerten (Rechnen). Als Beispiel sei hier die schriftliche Addition genannt: Unter Verwendung der Darstellung von Zahlen in einem Stellenwertsystem ist es hier möglich, durch systematisches Abarbeiten der Ziffern eine Darstellung für die Summe der beiden Zahlen zu erlangen. In der Informatik und der numerischen Mathematik werden solche Verfahren entwickelt und auf ihre Leistungsfähigkeit hin untersucht. Einige solcher Verfahren sind von fundamentaler Bedeutung für die heutigen Computer.

In der abstrakten Algebra befasst man sich mit der Struktur von Verallgemeinerungen solcher Zahlbereiche, wobei nur noch das Vorhandensein von Verknüpfungen mit gewissen Eigenschaften über einer beliebigen Menge von Objekten vorausgesetzt wird, welche die Struktur der Verknüpfungen nicht eindeutig bestimmen, sondern viele verschiedene konkrete Strukturen mit diesen Eigenschaften (Modelle) zulassen (siehe algebraische Struktur). Ihre Resultate lassen sich auf konkrete Zahlbereiche anwenden, die wiederum in der abstrakten Algebra als Motivation und elementare Beispiele dienen können.

Die Zahlentheorie behandelt Eigenschaften (im weiteren Sinne) von Zahlen, etwa Existenz, Häufigkeit und Verteilung von Zahlen mit bestimmten Eigenschaften. Eigenschaften transfiniter (in bestimmten Sinnen „unendlicher“) Zahlen sind allerdings Gegenstand der Mengenlehre.

In der Mathematik werden solche Verknüpfungen, Beziehungen und Eigenschaften als Prädikate oder Relationen, einschließlich Funktionen, aufgefasst.

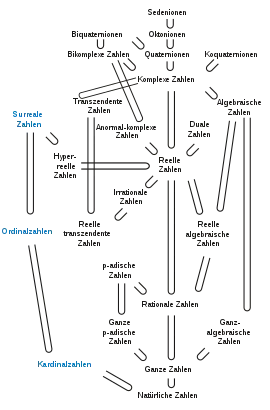
Zahlbereiche

Einige wichtige Zahlbereiche seien hier in ihrem mathematischen Kontext vorgestellt. Im Laufe der Geschichte der Mathematik wurden immer weitere Zahlbereiche eingeführt, um gegenüber bisherigen Zahlbereichen bestimmte Probleme allgemeiner behandeln zu können. Insbesondere wurden bestehende Zahlbereiche durch Hinzufügen zusätzlicher Elemente zu neuen Zahlbereichen erweitert, um über gewisse Operationen allgemeiner sprechen zu können, siehe hierzu auch den Artikel zur Zahlbereichserweiterung.

Zum Begriff des Zahlbereichs siehe den Abschnitt zur Definition.

Natürliche Zahlen

Die natürlichen Zahlen 1, 2, 3, 4, 5, … oder 0, 1, 2, 3, 4, 5, … bilden diejenige Menge von Zahlen, die üblicherweise zum Zählen verwendet wird, wobei je nach Definition die Null mit eingeschlossen wird oder nicht. Die natürlichen Zahlen sind mit einer Ordnung („kleiner“) versehen. Es gibt ein kleinstes Element (je nach Definition die Null oder die Eins), und jedes Element hat einen Nachfolger und ist kleiner als sein Nachfolger. Indem man ausgehend vom kleinsten Element immer wieder den Nachfolger bildet, erreicht man schließlich jede natürliche Zahl und sukzessive immer weitere, so dass es ihrer unendlich viele gibt. Die natürlichen Zahlen sind zudem mit Addition und Multiplikation versehen, je zwei natürlichen Zahlen lassen sich damit eine Summe und ein Produkt zuordnen, die wieder natürliche Zahlen sind. Diese Operationen sind assoziativ und kommutativ, zudem sind sie im Sinne des Distributivgesetzes miteinander verträglich: $a\cdot (b+c)=a\cdot b+a\cdot c$ . Diese drei Eigenschaften sind auch grundlegend für viele allgemeinere Zahlbereiche wie die ganzen, rationalen, reellen und komplexen Zahlen. Die Ordnung der natürlichen Zahlen ist in gewisser Hinsicht mit der Addition und Multiplikation verträglich: Sie ist verschiebungsinvariant, d. h., für natürliche Zahlen $m,n,o$ folgt aus $m\leq n$ auch $m+o\leq n+o$ , zusätzlich zur Verschiebungsinvarianz folgt auch $m\cdot o\leq n\cdot o$ .

Die Existenz der Menge aller natürlichen Zahlen wird in der Mengenlehre durch das Unendlichkeitsaxiom sichergestellt.

Diese Menge wird mit $\mathbb {N}$ oder $\mathbf {N}$ bezeichnet.

Ganze Zahlen

In der Menge der natürlichen Zahlen existiert für zwei Zahlen $n<m$ keine natürliche Zahl $d$ , sodass $m+d=n$ . Die ganzen Zahlen erweitern die natürlichen Zahlen so, dass für zwei beliebige Elemente eine solche Zahl $d$ existiert. Hierzu fügt man die negativen Zahlen den natürlichen Zahlen hinzu: Zu jeder natürlichen Zahl $n$ existiert eine zweite ganze Zahl $-n$ , so dass $n+(-n)=0$ , welche als additives Inverses bezeichnet wird. Die obige Zahl $d$ , genannt Differenz, ist dann als $n+(-m)$ , kurz $n-m$ , gegeben. Hierdurch ist die Subtraktion auf den ganzen Zahlen definiert, die jedoch im Wesentlichen eine Kurzschreibweise darstellt.

Die Ordnung über den natürlichen Zahlen wird auf die ganzen Zahlen erweitert. Hierbei gibt es kein kleinstes Element mehr; dafür hat jedes Element einen Vorgänger und einen Nachfolger (der Vorgänger der $0$ ist die $-1$ , der der $-1$ die $-2$ etc.). Die Verträglichkeit mit der Addition, die Verschiebungsinvarianz, bleibt dabei erhalten. Zudem ist das Produkt von zwei ganzen Zahlen größer Null stets wiederum größer Null.

Die ganzen Zahlen bilden einen Ring.

Die Menge der ganzen Zahlen wird mit $\mathbb {Z}$ oder $\mathbf {Z}$ bezeichnet.

Rationale Zahlen

Ebenso wie die natürlichen Zahlen zu den ganzen Zahlen erweitert werden, um ein additives Inverses und die Subtraktion zu erhalten, erweitert man die ganzen Zahlen zu den rationalen Zahlen, um ein multiplikatives Inverses und die Division zu erhalten. D. h., die rationalen Zahlen enthalten die ganzen Zahlen, und zu jeder ganzen Zahl $z\neq 0$ fügt man die ${\tfrac {1}{z}}$ genannte Zahl (Stammbruch) als multiplikatives Inverses hinzu, so dass $\textstyle z\cdot {\frac {1}{z}}=1$ . Zudem soll das Produkt zweier beliebiger rationaler Zahlen definiert sein, allgemein erhält man rationale Zahlen der Form $\textstyle {\frac {x}{y}}=x\cdot {\frac {1}{y}}$ , genannt Bruch, wobei eine ganze Zahl $z$ mit dem Bruch $\textstyle {\frac {z}{1}}$ identifiziert wird. Für ganze Zahlen $t\neq 0$ werden die Brüche $\textstyle {\frac {x}{y}}$ und $\textstyle {\frac {t\cdot x}{t\cdot y}}$ miteinander identifiziert; diese Identifizierung wird auch als Erweitern und Kürzen bezeichnet. Somit erhält man eine mit der Multiplikation ganzer Zahlen kompatible Multiplikation und Division.

Mittels der Dezimalbruchdarstellung lässt sich eine mit der Ordnung der ganzen Zahlen kompatible Ordnung definieren, die auch die Verträglichkeit mit Addition und Multiplikation erhält.

Die rationalen Zahlen bilden einen (geordneten) Körper. Die Konstruktion der rationalen Zahlen aus den ganzen Zahlen wird verallgemeinert als Quotientenkörperbildung zu einem Ring.

Die Menge der rationalen Zahlen wird mit $\mathbb {Q}$ oder $\mathbf {Q}$ bezeichnet. In der (deutschen) Schulmathematik kommt daneben die Bezeichnung $\mathbb {B} (:=\mathbb {Q} _{0}^{+})$ vor („Menge der (positiven) Bruchzahlen“), wenn die positiven Brüche vor den negativen ganzen Zahlen eingeführt werden.

Algebraische Erweiterungen

Mit der Addition und Multiplikation ganzer oder rationaler Zahlen lassen sich sogenannte Polynomfunktionen definieren: Jeder ganzen bzw. rationalen Zahl wird dabei eine Summe von Potenzen multipliziert mit konstanten Zahlen (Koeffizienten) zugeordnet. Etwa einer beliebigen Zahl $x$ der Wert $\textstyle 12\cdot x^{0}+4\cdot x^{2}+\left(-{\frac {1}{2}}\right)\cdot x^{3}$ definiert als $\textstyle 12+4\cdot x\cdot x+\left(-{\frac {1}{2}}\right)\cdot x\cdot x\cdot x$ . Für viele solcher Polynomfunktionen existiert keine rationale Zahl, so dass der Wert der Polynomfunktion an dieser Stelle gleich Null wird (Nullstelle). Fügt man nun Nullstellen bestimmter Polynomfunktionen den rationalen Zahlen hinzu, wobei Multiplikation und Addition wohldefiniert bleiben, erhält man eine algebraische Erweiterung. Erweitert man die rationalen Zahlen um solche Nullstellen für alle nicht-konstanten Polynome, erhält man die algebraischen Zahlen. Erweitert man die ganzen Zahlen um Nullstellen für alle nicht-konstanten Polynome, deren Koeffizienten ganzzahlig sind und deren Koeffizient zur höchsten Potenz $1$ ist, so erhält man die ganzalgebraischen Zahlen.

Algebraische Erweiterungen werden in der Körpertheorie, insbesondere in der Galois-Theorie, untersucht.

Reelle Zahlen

Betrachtet man Probleme wie etwa das Finden von Nullstellen von Polynomfunktionen über den rationalen Zahlen, stellt man fest, dass sich in den rationalen Zahlen beliebig gute Näherungen konstruieren lassen: Etwa findet sich bei zahlreichen Polynomfunktionen zu jeder festgelegten Toleranz eine rationale Zahl, so dass der Wert der Polynomfunktion an dieser Stelle höchstens um die Toleranz von der Null abweicht. Zudem kann man die Näherungslösungen so wählen, dass sie „nah beieinander“ liegen, denn Polynomfunktionen sind stetig („weisen keine ‚Sprünge‘ auf“). Dieses Verhalten tritt nicht nur bei Nullstellen von Polynomfunktionen auf, sondern auch bei zahlreichen weiteren mathematischen Problemen, die eine gewisse Stetigkeit aufweisen, so dass man dazu übergeht, die Existenz einer Lösung zu garantieren, sobald beliebig gute Näherungen durch nahe beieinander gelegene rationale Zahlen existieren. Eine solche Lösung nennt man eine reelle Zahl. Um die Existenz solcher Lösungen zu zeigen, reicht es, zu fordern, dass es zu jeder Menge rationaler Zahlen, die nicht beliebig große Zahlen enthält, unter den reellen Zahlen, die größer oder gleich als all diese Elemente der Menge sind, eine kleinste gibt. Alternativ lassen sich die reellen Zahlen explizit als Folgen von rationalen Zahlen, die sich einander „annähern“, definieren.

Die Menge der reellen Zahlen ist überabzählbar. Daher ist es nicht möglich, jede beliebige reelle Zahl sprachlich eindeutig zu beschreiben.

Die Abgeschlossenheit der reellen Zahlen unter solchen Näherungsprozessen bezeichnet man als Vollständigkeit. Diese erlaubt es, zahlreiche Begriffe aus der Analysis, wie den der Ableitung und den des Integrals, über Grenzwerte zu definieren. Grenzwerte erlauben zudem die Definition zahlreicher wichtiger Funktionen, etwa der trigonometrischen Funktionen (Sinus, Cosinus, Tangens etc.), was über den rationalen Zahlen nicht möglich ist.

Die reellen Zahlen behalten maßgebliche Eigenschaften der Addition, Multiplikation und der Ordnung in den rationalen Zahlen und bilden somit ebenfalls einen geordneten Körper. Sie lassen sich nicht erweitern, ohne diese Eigenschaft oder das archimedische Axiom zu verletzen, also „unendlich kleine strikt positive Zahlen“ einzuführen.

Die Idee des Übergangs von den rationalen zu den reellen Zahlen wird durch verschiedene Konzepte der Vervollständigung verallgemeinert.

Die Menge der reellen Zahlen wird mit $\mathbb {R}$ oder $\mathbf {R}$ bezeichnet.

Komplexe Zahlen

Manche Polynomfunktionen besitzen keine Nullstellen in den reellen Zahlen. Beispielsweise nimmt die Funktion $x\mapsto x^{2}+1$ für jede reelle Zahl $x$ einen Wert größer als Null an. Es lässt sich zeigen, dass durch Hinzufügen einer Zahl $i$ , genannt imaginäre Einheit, die die Gleichung $i^{2}+1=0$ erfüllt, wobei die grundlegenden Eigenschaften der Addition und Multiplikation erhalten bleiben sollen, bereits die reellen Zahlen zu den komplexen Zahlen erweitert werden, in denen alle nicht konstanten Polynomfunktionen eine Nullstelle besitzen. Die komplexen Zahlen bilden damit den algebraischen Abschluss der reellen Zahlen. Grenzwertprozesse sind in den komplexen Zahlen ebenso möglich wie in den reellen Zahlen, jedoch sind die komplexen Zahlen nicht mehr geordnet. Sie lassen sich als Ebene (zweidimensionaler Vektorraum über den reellen Zahlen) auffassen. Jede komplexe Zahl lässt sich eindeutig in der Form $a+b\cdot i$ „darstellen“, wobei $a$ und $b$ reelle Zahlen sind und $i$ die imaginäre Einheit bezeichnen.

Die Funktionentheorie ist das Teilgebiet der Analysis, das sich mit den analytischen Eigenschaften von Funktionen über den komplexen Zahlen befasst.

Die Menge der komplexen Zahlen wird mit $\mathbb {C}$ oder $\mathbf {C}$ bezeichnet.

Ordinalzahlen und Kardinalzahlen

Die Ordinal- und Kardinalzahlen sind Konzepte aus der Mengenlehre. In der Mengenlehre definiert man die Kardinalität einer Menge als Kardinalzahl, die Kardinalität ist eine Verallgemeinerung des Konzepts der „Anzahl der Elemente“ einer endlichen Menge auf unendliche Mengen. Die Kardinalitäten endlicher Mengen sind somit natürliche Zahlen, die auch in den Kardinalzahlen enthalten sind.

Ordinalzahlen verallgemeinern das Konzept der „Position in einer (wohlgeordneten) Menge“ auf unendliche Mengen. Ordinalzahlen beschreiben dann eindeutig die Position eines Elementes in einer solchen Wohlordnung. Die Ordinalzahlen sind selbst wohlgeordnet, so dass die Reihenfolge von wohlgeordneten Objekten der Reihenfolge der ihnen zugeordneten „Positionen“ (also Ordinalzahlen) entspricht. Für Positionen in Anordnungen endlich vieler Objekte lassen sich natürliche Zahlen verwenden, die den kleinsten Ordinalzahlen entsprechen.

Kardinalzahlen werden heutzutage als spezielle Ordinalzahlen definiert, wodurch sie ebenfalls eine Ordnung erhalten. Neben der Ordnung sind auf Kardinalzahlen und Ordinalzahlen auch Addition, Multiplikation und Potenzierung definiert, die eingeschränkt auf die natürlichen Zahlen mit den üblichen Begriffen für natürliche Zahlen übereinstimmen, siehe hierzu Kardinalzahlarithmetik und transfinite Arithmetik.

Sowohl die Ordinalzahlen als auch die Kardinalzahlen bilden echte Klassen, das heißt, sie sind im Sinne der modernen Mengenlehre keine Mengen.

Hyperreelle Zahlen

Die hyperreellen Zahlen sind eine Verallgemeinerung der reellen Zahlen und Untersuchungsgegenstand der Nichtstandardanalysis. Sie erlauben die Definition von Begriffen aus der Analysis, etwa die der Stetigkeit oder der Ableitung, ohne die Verwendung von Grenzwerten.

Hyperkomplexe Zahlen

Die komplexen Zahlen lassen sich als zweidimensionaler Vektorraum über den reellen Zahlen auffassen (siehe Gaußsche Zahlenebene), das heißt als zweidimensionale Ebene, bei der neben der üblichen koordinatenweisen Addition eine Multiplikation zwischen zwei Punkten der Ebene definiert ist. Es gibt zahlreiche ähnliche Strukturen, die man unter dem Begriff hyperkomplexe Zahlen zusammenfasst. Diese Strukturen sind in der Regel endlichdimensionale Vektorräume über den reellen Zahlen (vorstellbar als zwei- oder höherdimensionaler Raum) mit einer zusätzlichen Multiplikation. Oftmals lassen sich die reellen Zahlen selbst in diese Strukturen einbetten, wobei die Multiplikation eingeschränkt auf die reellen Zahlen der üblichen Multiplikation von reellen Zahlen entspricht.

Weitere Gruppen von Zahlen

p-adische Zahl, eine Verallgemeinerung der rationalen Zahlen unter Miteinbeziehung von unendlich vielen „Vorkomma-Stellen“, die in der Zahlentheorie Verwendung findet.
Surreale Zahl, eine Verallgemeinerung der hyperreellen Zahlen und der Ordinalzahlen mit Anwendungen in der Spieltheorie.
Restklassenringe können als Einschränkungen der ganzen Zahlen auf die ersten endlich vielen Elemente mit entsprechend definierter Arithmetik aufgefasst werden. Ihre Elemente werden mitunter auch als Zahlen bezeichnet.

Darstellung von Zahlen

In der Mathematik spricht man mittels der Sprache der Logik über in dieser definierte mathematische Objekte wie etwa Zahlen, mit ihr lassen sich auch konkrete Zahlen mitunter eindeutig beschreiben, unter Umständen mittels Formeln. Über die gängigen logischen Formalismen hinaus existieren jedoch systematische Bezeichnungen für bestimmte Zahlen, etwa in Form von speziellen Kombinationen von Schriftzeichen (mitunter eigens dafür verwendete Ziffern) oder mittels besonders konstruierter Wörter der natürlichen Sprache, wie etwa Numerale. Bezeichnungen für bestimmte Zahlen werden außerhalb der Mathematik verwendet, um konkrete Beobachtungen zu beschreiben, etwa eine Anzahl beobachteter Objekte (Ich sehe fünf Bananen) oder mittels eines anderen Messverfahrens bestimmte Messwerte (Der Türrahmen ist zwei Meter hoch). Des Weiteren erlauben solch systematische Zahldarstellungen mitunter einfaches, systematisches Rechnen mit konkreten Zahlen – gerade auch durch Rechenmaschinen und Computer. Die Rechenverfahren zur Berechnung gewisser Operationen zwischen konkreten Zahlen hängen von der gewählten Darstellung ab.

In der Kultur- und Mathematikgeschichte haben sich zahlreiche Zahlensysteme zu solchen systematischen Zahldarstellungen entwickelt. Belege für die Darstellung von Zahlen reichen bis in die späte Steinzeit zurück, wobei Schwierigkeiten bestehen, Zahlzeichen von bloßen Zählzeichen zu unterscheiden, das heißt zu erkennen, ob den Menschen Zahlen als abstrakte Bedeutung jener bewusst waren, oder nur eine werkzeugartige Verwendung vorlag, bei denen die physische Konstruktion des Zählzeichens, nicht aber eine Bedeutung relevant war, seine Aufgabe zu erfüllen. Zu dieser Problematik siehe etwa den Artikel zum Ishango-Knochen, einem Fund aus der späten Altsteinzeit, der verschiedenartige Interpretationen zulässt.

Beispiele für solche Darstellungen sind Strichlisten (Unärsystem) und die Ziffernfolgen verwendenden Stellenwertsysteme, wie sie heute für die Darstellung natürlicher Zahlen üblich sind und auch für die Zahldarstellung in Computern in Form des Dualsystems verwendet werden.

Betrachtet man sprachliche Darstellungen von Zahlen formal, so lässt sich nicht jeder Zahl eine solche Darstellung in einem formalen Sinne zuordnen, d. h., in einem mathematischen formalen Sinne existieren mehr Zahlen als mögliche Darstellungen in einer Sprache: Da sprachliche Formulierungen stets endlich sind, kann es von ihnen nur abzählbar viele verschiedene geben, während die Mathematik auch überabzählbare Zahlbereiche betrachtet. Man spricht dennoch auch von Darstellungen überabzählbarer Zahlbereiche, wenn man sich bei solchen formalen Darstellungen nicht mehr auf zu sprachlichen Formulierungen korrespondierende beschränkt, in ihrer Struktur können sie jedoch den Zahlensystemen ähneln, etwa lassen sich die reellen Zahlen als spezielle formale Reihen definieren, welche der Darstellung in Stellenwertsystemen strukturell ähneln.

Beispiele

Einige Beispiele für Darstellungen von Zahlen:

„Vier“ bezeichnet im Deutschen als Zahlwort eine Zahl.
Diese Zahl lässt sich als Strichliste |||| darstellen.
In der indisch-arabischen Zahlschrift wird sie als 4 dargestellt.
In der römischen Zahlschrift wird sie als IV dargestellt.
Als Formel lässt sie sich z. B. als $1+1+1+1$ darstellen, was einer mathematischen Definition gleichkommt, falls die Eins und die Addition zuvor definiert worden sind.
Fasst man die natürlichen Zahlen als algebraische Struktur versehen mit Multiplikation und Addition auf, so lässt sich die Eins als einzige natürliche Zahl $x$ definieren, so dass $x\cdot x=x$ und $x+x\neq x$ , das Symbol $1$ steht dann für eine beliebige natürliche Zahl, die diese Bedingung erfüllt, und ist damit eindeutig.
Definiert man natürliche Zahlen mengentheoretisch in der Variante von John von Neumann, so lässt sich die Vier über die übliche Darstellung endlicher Mengen als $\left\{\emptyset ,\left\{\emptyset \right\},\left\{\emptyset ,\left\{\emptyset \right\}\right\},\left\{\emptyset ,\left\{\emptyset \right\},\left\{\emptyset ,\left\{\emptyset \right\}\right\}\right\}\right\}$ darstellen.
Rationale Zahlen lassen sich als Brüche darstellen, z. B. ${\tfrac {1}{2}}$ .
Lösungen quadratischer Gleichungen über den rationalen Zahlen lassen sich als Formeln, bestehend aus Addition, Multiplikation und Quadratwurzelbildung rationaler Zahlen darstellen. Beispielsweise beschreibt die Formel ${\sqrt {2}}$ eine Lösung der Gleichung $x^{2}=2$ für die Variable $x$ .
Komplexe Zahlen werden oft als Summe von Realteil und dem Imaginärteil multipliziert mit der imaginären Einheit dargestellt, etwa $\textstyle -{\frac {4}{3}}+{\frac {9}{2}}\cdot i$ .
Im Dualsystem wird die natürliche Zahl Neun als $1001$ dargestellt, dies entspricht der Darstellung als Formel $1\cdot 2\cdot 2\cdot 2+0\cdot 2\cdot 2+0\cdot 2+1$ .
Jede reelle Zahl lässt sich als Reihe $\textstyle z+\sum _{i=1}^{\infty }a_{i}\cdot 2^{-i}$ mit einer ganzen Zahl $z$ und Koeffizienten $a_{i}\in \left\{0,1\right\}$ „darstellen“, solche Darstellungen sind jedoch im Allgemeinen nicht endlich beschreibbar, da es überabzählbar viele mögliche „Belegungen“ der Koeffizienten gibt. Falls $a_{i}$ für hinreichend große $i$ stets Null wird, entsprechen die $a_{i}$ dem Nachkommateil in einer Darstellung im Dualsystem (etwa $0{,}101$ für $0{,}625$ ).

Zahlen als Bezeichnung

Ebenso wie Zahlen sprachliche Ausdrücke, Zeichenketten oder dergleichen zugeordnet werden, können umgekehrt Zahlen bestimmten Objekten zugeordnet werden, zum einen für abstrakte Überlegungen, zum anderen, um Darstellungen von Zahlen konkret zur systematischen Bezeichnung von anderen Objekten einzusetzen, etwa Information mittels Zahlen zu kodieren. Solches Vorgehen erlaubt die Anwendung von den auf Zahlen definierten Operationen auf diese Bezeichnungen. Ein verbreitetes Beispiel ist die Nummerierung, bei der jedem Objekt einer bestimmten betrachteten Gesamtheit eine (meist natürliche) Zahl zugeordnet wird: Dies erlaubt zum einen die Benennung der Objekte mittels ihrer Nummern, und schafft zum anderen mittels der auf den natürlichen Zahlen definierten Ordnung („kleiner“) eine Ordnung der Objekte; dies erlaubt etwa im Falle natürlicher Zahlen ein sequentielles Durchgehen aller Objekte. Zu beachten ist, dass nicht jede Nummer eine Zahl als von der Darstellung unabhängiges mathematisches Objekt ist. Manche Nummern sind als spezielle Symbolfolgen zu verstehen, die als Identifikatoren dienen, selbst wenn sie nur aus Ziffern bestehen (z. B. ISB-, Versicherungs- oder Steuernummern).

Ein anderes Beispiel ist die Interpretation digitaler Information in der Datenverarbeitung: Als binäre Folge vorliegende Daten können auf natürliche Weise als natürliche Zahl, dargestellt im Dualsystem, interpretiert werden (Randfälle wie führende Nullen müssen dabei beachtet werden). Arithmetische Operationen über dieser Kodierung als Zahl werden u. a. in der Kryptographie und der Datenkompression eingesetzt.

Auch in der reinen Mathematik finden sich Anwendungen dieses Prinzips, wobei üblicherweise nicht als Zahlen aufgefassten mathematischen Objekten Zahlen zugeordnet werden, etwa in Form von Gödelnummern, die logische Formeln oder Algorithmen identifizieren.

Weitere Beispiele sind die Repräsentation von Spielsituationen mittels surrealer Zahlen in der Spieltheorie, die Darstellung von Drehstreckungen im zweidimensionalen euklidischen Raum durch komplexe Zahlen sowie Drehungen im Dreidimensionalen mittels Quaternionen.

Siehe auch

Literatur

Albrecht Beutelspacher: Zahlen – Geschichte, Gesetze, Geheimnisse. C. H. Beck, München 2013, ISBN 978-3-406-64871-7.
John D. Barrow: Pi in the sky. Oxford University Press, London 1992, deutsch von Anita Ehlers: Ein Himmel voller Zahlen Auf den Spuren mathematischer Wahrheit., Rowohlt, Reinbek 1999, ISBN 3-499-19742-1.
Jürgen Brater: Kuriose Welt der Zahlen, Eichborn Verlag, Frankfurt/Main 2005, ISBN 3-8218-4888-X.
Tobias Dantzig: Number. The Language of Science. Pi Press, New York 2005, ISBN 0-13-185627-8 (englisch, Originaltitel: Number, the language of science; a critical survey written for the cultured non-mathematician. Erstausgabe: Macmillan Co., New York 1930).
Heinz-Dieter Ebbinghaus et al.: Zahlen. 3. Auflage. Springer, Berlin 1992, ISBN 3-540-55654-0.
Graham Flegg (Hrsg.): Numbers Through the Ages. Macmillan Education, Basingstoke et al. 1989, ISBN 978-0-333-49131-7.
Georges Ifrah: Universalgeschichte der Zahlen. Parkland, Köln 1998, ISBN 3-88059-956-4.
Heinz Lüneburg: Von Zahlen und Größen. Dritthalbtausend Jahre Theorie und Praxis. Birkhäuser, Basel 2008, ISBN 978-3-7643-8776-1.
Uta Merzbach, Carl Benjamin Boyer: A History of Mathematics. John Wiley & Sons, 2011, ISBN 978-0-470-52548-7.
Albert J. Urban (Hrsg.): Zahlen – Maße, Einheiten und Symbole, area verlag gmbh, Erftstadt 2005, ISBN 3-89996-413-6.
Kurt Vogel: Vorgriechische Mathematik I: Vorgeschichte und Ägypten. Schroedel, Hannover und Schöningh, Paderborn 1958.
Kurt Vogel: Vorgriechische Mathematik II: Die Mathematik der Babylonier. Schroedel, Hannover und Schöningh, Paderborn 1959.
Hans-Ludwig Wußing: 6000 Jahre Mathematik. Eine kulturgeschichtliche Zeitreise. Von den Anfängen bis Leibniz und Newton. Springer, Berlin u. a. 2008, ISBN 978-3-540-77189-0.

Weblinks

Commons: Numbers – Album mit Bildern, Videos und Audiodateien

Wikibooks: ${\color {BlueViolet}{\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$ Mathematik für die Schule – Zahlenmengen

Wiktionary: Zahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Geschichte und Soziologie globaler Zahlen. Tagungsbericht auf H-Soz-Kult
Meyers Großes Konversations-Lexikon, Band 20. Leipzig 1909, S. 832-833, Henricus – Edition Deutsche Klassik GmbH

Einzelnachweise

John Bigelow, Sam Butchart: Number. In: Donald M. Borchert (Hrsg.): Encyclopedia of Philosophy. 2005, ISBN 0-02-866072-2.
Schon der Neandertaler war kreativ. RP online, abgerufen am 5. März 2022.
Merzbach, Boyer, S. 198.
Vladimir Orel: A Handbook of Germanic Etymology. Brill, Leiden 2003, S. 400 f.; archive.org
August Fick: Wörterbuch der Indogermanischen Sprachen. Dritter Teil: Wortschatz der Germanischen Spracheinheit. (PDF; 2,7 MB). Vandenhoeck & Ruprecht, Göttingen 1909.
Zahl. In: Jacob Grimm, Wilhelm Grimm (Hrsg.): Deutsches Wörterbuch. Band 31: Z–Zmasche – (XV). S. Hirzel, Leipzig 1956, Sp. 36–42 (woerterbuchnetz.de).
Julius Pokorny: Indogermanisches etymologisches Wörterbuch. Francke, Bern 1959, Band I, S. 193; archive.org, Datenbankeintrag
Friedrich Kluge, Elmar Seebold: Etymologisches Wörterbuch der deutschen Sprache. 24. Auflage. de Gruyter, Berlin 2002, ISBN 3-11-017472-3., S. 1002.
Zahl. In: Duden, abgerufen am 11. Juni 2012.
Flegg, S. 7 ff.
Ebbinghaus et al., S. 311
Vogel, I, S. 14
Michael C. Frank, Daniel L. Everett, Evelina Fedorenko, Edward Gibson: Number as a cognitive technology: Evidence from Pirahã language and cognition. In: Cognition. Band 108, Nr. 3. Elsevier, 2008, S. 819–824, doi:10.1016/j.cognition.2008.04.007 (stanford.edu [PDF; 328 kB; abgerufen am 23. Dezember 2012]).
Daniel L. Everett: Cultural Constraints on Grammar and Cognition in Pirahã. Another Look at the Design Features of Human Language. In: Current Anthropology. Band 46, Nr. 4. The Wenner-Gren Foundation for Anthropological Research, 2005 (pnglanguages.org [PDF; 961 kB; abgerufen am 23. Dezember 2012]).
Flegg, S. 7 ff.
Vogel, I, S. 14
Flegg, S. 56 ff.
Flegg, S. 7 ff.
Vogel, I, S. 15
Vogel, I, S. 15
Vogel, I, S. 14
Vogel, I, S. 15
Vogel, I, S. 15
Flegg, S. 7 ff.
Werner Hilgemann, Hermann Kinder: dtv-Atlas zur Weltgeschichte. 37. Auflage. Band 1. dtv, München 2004, ISBN 978-3-423-03001-4, S. 13 ff.
dtv-Atlas zur Weltgeschichte. Band 1, S. 17.
dtv-Atlas zur Weltgeschichte. Band 1, S. 16 f.
Dieter Vieweger: Archäologie der biblischen Welt. Vandenhoeck & Ruprecht, Göttingen 2003, ISBN 978-3-423-03001-4, S. 337 ff.
Merzbach, Boyer, S. 10
Howard Eves: An introduction to the history of mathematics. 3. Auflage. Saunders College Pub., Philadelphia 1990, ISBN 0-03-029558-0, S. 39.
Eves, S. 38.
Wußing, S. 121.
Wußing, S. 118.
Merzbach, Boyer, S. 14.
Eves, S. 40–41.
Merzbach, Boyer, S. 23–27.
Wußing, S. 140.
Merzbach, Boyer, S. 28–29.
Wußing, S. 142.
Merzbach, Boyer, S. 38.
Merzbach, Boyer, S. 44.
Merzbach, Boyer, S. 45.
Wußing, S. 174.
Merzbach, Boyer, S. 47.
Ebbinghaus, S. 26–27.
Matvievskaya, S. 253.
Wußing, S. 165.
David E. Joyce: Elemente – Buch 7, Definition 8.1. Abgerufen am 22. Dezember 2012.
Merzbach, Boyer, S. 70.
Merzbach, Boyer, S. 65–67.
Morris Kline: Mathematical Thought from Ancient to Modern Times. Band 1. Oxford University Press, New York / Oxford 1972, ISBN 0-19-506135-7, S. 48–49.
Ebbinghaus, S. 26–27.
Brad Rogers: A History of Real Numbers, and the First Crisis of Western Knowledge. (PDF; 94 kB) (Nicht mehr online verfügbar.) Archiviert vom Original am 3. Dezember 2011; abgerufen am 22. Dezember 2012.
Wußing, S. 263.
John J. O’Connor, Edmund F. Robertson: Eudoxus of Cnidus. In: MacTutor History of Mathematics archive.
Reviel Netz: Methods of Infinity. The Archimedes Palimpsest Project, abgerufen am 7. November 2012.
Richard Dedekind: Was sind und was sollen die Zahlen? 2. unv. Auflage. Verlag Friedrich Vieweg und Sohn, Braunschweig 1893, S. 7–8.
Jouko Väänänen: Second-Order Logic and Foundations of Mathematics. 2001, S. 19 (math.helsinki.fi [PDF; 194 kB; abgerufen am 2. Mai 2013]).
Stewart Shapiro: Foundations without Foundationalism. A Case for Second-order Logic. Oxford University Press, Oxford 1991, ISBN 0-19-853391-8, S. vii, 204 ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] John Bigelow, Sam Butchart: Number. In: Donald M. Borchert (Hrsg.): Encyclopedia of Philosophy. 2005, ISBN 0-02-866072-2.

[2] Schon der Neandertaler war kreativ. RP online, abgerufen am 5. März 2022.

[3] Merzbach, Boyer, S. 198.

[orel-4] Vladimir Orel: A Handbook of Germanic Etymology. Brill, Leiden 2003, S. 400 f.; archive.org

[fick-5] August Fick: Wörterbuch der Indogermanischen Sprachen. Dritter Teil: Wortschatz der Germanischen Spracheinheit. (PDF; 2,7 MB). Vandenhoeck & Ruprecht, Göttingen 1909.

[grimm-6] Zahl. In: Jacob Grimm, Wilhelm Grimm (Hrsg.): Deutsches Wörterbuch. Band 31: Z–Zmasche – (XV). S. Hirzel, Leipzig 1956, Sp. 36–42 (woerterbuchnetz.de).

[pokorny-7] Julius Pokorny: Indogermanisches etymologisches Wörterbuch. Francke, Bern 1959, Band I, S. 193; archive.org, Datenbankeintrag

[kluge"-8] Friedrich Kluge, Elmar Seebold: Etymologisches Wörterbuch der deutschen Sprache. 24. Auflage. de Gruyter, Berlin 2002, ISBN 3-11-017472-3., S. 1002.

[duden-9] Zahl. In: Duden, abgerufen am 11. Juni 2012.

[10] Flegg, S. 7 ff.

[11] Ebbinghaus et al., S. 311

[12] Vogel, I, S. 14

[13] Michael C. Frank, Daniel L. Everett, Evelina Fedorenko, Edward Gibson: Number as a cognitive technology: Evidence from Pirahã language and cognition. In: Cognition. Band 108, Nr. 3. Elsevier, 2008, S. 819–824, doi:10.1016/j.cognition.2008.04.007 (stanford.edu [PDF; 328 kB; abgerufen am 23. Dezember 2012]).

[14] Daniel L. Everett: Cultural Constraints on Grammar and Cognition in Pirahã. Another Look at the Design Features of Human Language. In: Current Anthropology. Band 46, Nr. 4. The Wenner-Gren Foundation for Anthropological Research, 2005 (pnglanguages.org [PDF; 961 kB; abgerufen am 23. Dezember 2012]).

[15] Flegg, S. 7 ff.

[16] Vogel, I, S. 14

[17] Flegg, S. 56 ff.

[18] Flegg, S. 7 ff.

[19] Vogel, I, S. 15

[20] Vogel, I, S. 15

[21] Vogel, I, S. 14

[22] Vogel, I, S. 15

[23] Vogel, I, S. 15

[24] Flegg, S. 7 ff.

[25] Werner Hilgemann, Hermann Kinder: dtv-Atlas zur Weltgeschichte. 37. Auflage. Band 1. dtv, München 2004, ISBN 978-3-423-03001-4, S. 13 ff.

[26] tv-Atlas zur Weltgeschichte. Band 1, S. 17.

[27] tv-Atlas zur Weltgeschichte. Band 1, S. 16 f.

[28] Dieter Vieweger: Archäologie der biblischen Welt. Vandenhoeck & Ruprecht, Göttingen 2003, ISBN 978-3-423-03001-4, S. 337 ff.

[29] Merzbach, Boyer, S. 10

[30] Howard Eves: An introduction to the history of mathematics. 3. Auflage. Saunders College Pub., Philadelphia 1990, ISBN 0-03-029558-0, S. 39.

[31] Eves, S. 38.

[32] Wußing, S. 121.

[33] Wußing, S. 118.

[34] Merzbach, Boyer, S. 14.

[35] Eves, S. 40–41.

[36] Merzbach, Boyer, S. 23–27.

[37] Wußing, S. 140.

[38] Merzbach, Boyer, S. 28–29.

[39] Wußing, S. 142.

[40] Merzbach, Boyer, S. 38.

[41] Merzbach, Boyer, S. 44.

[42] Merzbach, Boyer, S. 45.

[43] Wußing, S. 174.

[44] Merzbach, Boyer, S. 47.

[45] Ebbinghaus, S. 26–27.

[46] Matvievskaya, S. 253.

[47] Wußing, S. 165.

[48] David E. Joyce: Elemente – Buch 7, Definition 8.1. Abgerufen am 22. Dezember 2012.

[49] Merzbach, Boyer, S. 70.

[50] Merzbach, Boyer, S. 65–67.

[51] Morris Kline: Mathematical Thought from Ancient to Modern Times. Band 1. Oxford University Press, New York / Oxford 1972, ISBN 0-19-506135-7, S. 48–49.

[52] Ebbinghaus, S. 26–27.

[53] Brad Rogers: A History of Real Numbers, and the First Crisis of Western Knowledge. (PDF; 94 kB) (Nicht mehr online verfügbar.) Archiviert vom Original am 3. Dezember 2011; abgerufen am 22. Dezember 2012.

[54] Wußing, S. 263.

[mactutor-eudoxos-55] John J. O’Connor, Edmund F. Robertson: Eudoxus of Cnidus. In: MacTutor History of Mathematics archive.

[56] Reviel Netz: Methods of Infinity. The Archimedes Palimpsest Project, abgerufen am 7. November 2012.

[57] Richard Dedekind: Was sind und was sollen die Zahlen? 2. unv. Auflage. Verlag Friedrich Vieweg und Sohn, Braunschweig 1893, S. 7–8.

[58] Jouko Väänänen: Second-Order Logic and Foundations of Mathematics. 2001, S. 19 (math.helsinki.fi [PDF; 194 kB; abgerufen am 2. Mai 2013]).

[59] Stewart Shapiro: Foundations without Foundationalism. A Case for Second-order Logic. Oxford University Press, Oxford 1991, ISBN 0-19-853391-8, S. vii, 204 ff.