Geschichte der Wahrscheinlichkeitsrechnung

Die Geschichte der Wahrscheinlichkeitsrechnung oder Stochastik beschreibt die Entwicklung eines gleichzeitig alten und modernen Teilgebiets der Mathematik, das sich mit der mathematischen Analyse von Experimenten mit unsicherem Ausgang befasst. Während viele heute noch gebräuchliche Formeln zu einfachen Zufallsprozessen möglicherweise bereits im Altertum, spätestens jedoch im ausgehenden Mittelalter bekannt waren, hat sich das heute verwendete axiomatische Fundament der Wahrscheinlichkeitstheorie erst zu Beginn des 20. Jahrhunderts herausgebildet; als Schlüsselereignisse gelten dabei zum einen ein Briefwechsel zwischen Blaise Pascal und Pierre de Fermat im Jahr 1654, gemeinhin als Geburtsstunde der klassischen Wahrscheinlichkeitsrechnung angesehen, und zum anderen das Erscheinen von Andrei Kolmogorows Lehrbuch Grundbegriffe der Wahrscheinlichkeitsrechnung im Jahr 1933, das die Entwicklung der Fundamente moderner Wahrscheinlichkeitstheorie abschloss. Dazwischen war es über Jahrhunderte hinweg zur Aufspaltung der klassischen Wahrscheinlichkeitstheorie in separate Schulen gekommen; diese wurden in erster Linie von den damaligen wissenschaftlichen Zentren London und Paris dominiert.

Roulettespieler, um 1800. Das Glücksspiel war eine der frühesten Triebfedern der Wahrscheinlichkeitsrechnung.

Titelblatt der Ars Conjectandi von Jakob I Bernoulli aus dem Jahr 1713, eines der Werke zur Stochastik im 18. Jahrhundert

Im Laufe der Zeit wurde die Stochastik von einer Vielzahl unterschiedlicher Anwendungsgebiete geprägt. War es zunächst das Interesse der Griechen und Römer an Glücksspielen, welches die Entwicklung von Rechenmodellen vorantrieb, so kamen Anregungen später auch aus der Philosophie, der Rechtswissenschaft und aus dem Versicherungswesen, noch später aus der Physik und heute in erster Linie aus der Finanzmathematik. Auf dem Umweg über die Statistik hat die Wahrscheinlichkeitsrechnung letztendlich Anwendung in praktisch allen quantitativ arbeitenden Wissenschaften gefunden.

Ausgangslage

Die Stochastik entwickelte sich langsamer und weniger zielstrebig als andere mathematische Disziplinen wie etwa die Analysis. Von Anfang an hatte sie mit schwerwiegenden Problemen zu kämpfen, die teilweise auf die Eigentümlichkeiten des Wahrscheinlichkeitsbegriffs an sich, teilweise auf Vorbehalte von Seiten anderer Wissenschaften wie Theologie, Philosophie und sogar der Mathematik selbst zurückzuführen sind.

Definition der Wahrscheinlichkeit

Eine Möglichkeit der Anwendung von Mathematik ist der Versuch einer Erfassung der Welt in Zahlen. Während die Konkretisierung von Zahlkonzepten für Größen wie Länge, Masse oder Zeit durch eine Messung – also den Vergleich mit einer (normierten) Maßeinheit wie der standardisierten Einheit einer Basisgröße – gelingt, blieb die quantitative Erfassung von Wahrscheinlichkeiten lange Zeit problematisch. Ein Wahrscheinlichkeitsmaß exakt zu definieren und so auch den damit implizierten Begriff der Wahrscheinlichkeit, gelang erst 1933 durch die Axiome von Kolmogorow. Damit wurde jedoch nicht geklärt, was Wahrscheinlichkeit explizit wäre, sondern nur herausgearbeitet, welche strukturellen Merkmale ein Wahrscheinlichkeitsmaß erfüllen muss, um brauchbar zu sein. Die Interpretation der Axiome bleibt insoweit noch eine offene Frage und hier bestehen weiterhin unterschiedliche Auffassungen.

Im Laufe der Zeit bildeten sich zwei Denkschulen, die unabhängig voneinander bestanden, ohne sich gegenseitig auszuschließen. Der Frequentismus entstand im Zuge der Untersuchung von Glücksspielen als standardisierte und beliebig oft unter gleichbleibenden Bedingungen wiederholbare Zufallsexperimente. Hier zeigte die Beobachtung, dass die relative Häufigkeit eines Experimentsausgangs mit zunehmender Wiederholungsanzahl konvergiert. Nach frequentistischer Definition entspricht die Wahrscheinlichkeit eines Ereignisses genau diesem Grenzwert – oder wie es der französische Stochastiker Paul Lévy ausdrückte: „Die Wahrscheinlichkeit ist wie die Masse von Gegenständen eine physikalische Größe, und die Häufigkeit ist ein Messinstrument für diese Größe, die wie alle physikalischen Messinstrumente mit gewissen unvorhersehbaren Messfehlern behaftet ist.“[1] So einleuchtend diese Definition im Falle von Glücksspielen oder auch in der Physik ist, so unbrauchbar erscheint sie für Prozesse, die nicht wiederholt werden können.

Dieses Problem besteht nicht, wenn man die Wahrscheinlichkeitsauffassung der zweiten Denkschule, des Bayesianismus, heranzieht. Hier ist Wahrscheinlichkeit ein Maß dafür, wie sehr man vom Eintreten eines gewissen Ereignisses überzeugt ist. Dabei spielt es formal keine Rolle, ob das Ereignis tatsächlich zufällig ist, oder ob der Ausgang lediglich unbekannt ist. Dieser pragmatische Zugang ermöglicht es, auf philosophische Vorüberlegungen zum Wesen und zur Existenz des Zufalls zu verzichten – ein Umstand, der diese Auffassung vor allem in der Statistik beliebt macht. Ein wesentlicher Nachteil ist, dass die Definition über die Überzeugung des Betrachters eine unerwünschte Subjektivität einführt. Dazu kommt, dass die Wahrscheinlichkeit hier im Gegensatz zum Frequentismus nicht intuitiv auf eine mathematisch sinnvolle numerische Skala abgebildet werden kann. Zur Abbildung müssen Gedankenexperimente der Form „Wie viel wären Sie bereit, auf das Eintreffen dieses Ereignisses zu wetten?“ herangezogen werden, was wiederum unvermeidlich zu Schwierigkeiten beim Thema Risikoaversion führt.

Obwohl nicht grundsätzlich unvereinbar, so haben diese beiden ideologisch verschiedenen Ansätze doch lange Zeit verhindert, dass sich eine einheitliche mathematische Theorie und eine einheitliche Notation herausbildeten.

Skepsis von Seiten anderer Wissenschaften

Über Jahrhunderte zog sich die Wahrscheinlichkeitsrechnung immer wieder die Skepsis anderer wissenschaftlicher Disziplinen zu. Dies kann man auf zwei Aspekte oder Gründe zurückführen:

die Begriffe Zufall und Wahrscheinlichkeit lassen sich nur mit Mühe definieren und wissenschaftlich quantifizieren.
Jeder Versuch, andernfalls nicht oder nur unzureichend prognostizierbare Phänomene (etwa das Wetter, Börsenkurse oder den Ausgang eines Würfelwurfs) stochastisch zu deuten, konnte als Konkurrenz zu einer anderen Wissenschaft gesehen werden.

Von Seiten der Theologie und der Kirche etwa wurde der Versuch, mit Wahrscheinlichkeitsrechnung den „unergründlichen Wegen des Herrn“ näher zu kommen, die man tagtäglich in der Natur beobachten konnte, lange als Blasphemie bezeichnet – die Begriffe Zufall und Schicksal liegen nahe beisammen. Zusätzlich störte man sich von Seiten der Kirche daran, dass in frühen Jahren das Hauptanwendungsgebiet im Glücksspiel lag, das sie seit jeher ablehnte. Bemerkenswert erscheint, dass Zufallsprozesse sowohl im alten (Orakelsteine Urim und Tummim, Exodus 28,30) als auch im neuen Testament (bei der Wahl des Matthias als Nachfolger des Judas durch Losentscheid, Apostelgeschichte 1,23–26) eine Rolle spielen, wenn es darum geht, Gottes Willen zu ergründen. In der Tradition des Widerstreits zwischen Christentum und Stochastik steht letztendlich auch die andauernde Debatte um Evolution und Kreationismus beziehungsweise Intelligent Design. Die Evolutionstheorie sieht die Entwicklung der Lebewesen als Ergebnis eines durch zufällige Mutationen angetriebenen, randomisierten Optimierungsprozesses, während Kreationisten dahinter einen festen Schöpfungsplan vermuten.

Doch auch die Naturwissenschaftler der Aufklärung begegneten der Stochastik mit Skepsis, da sie sie als „Bankrotterklärung“ vor der Natur betrachteten. Schließlich seien alle Phänomene durch deterministische Naturgesetze vollständig erklärbar, wenn man nur genau genug messe und alle Gesetze durch Experimente ergründe.[2] Somit gebe es so etwas wie Zufall überhaupt nicht, was auch die Existenz einer seriösen Wahrscheinlichkeitsrechnung ausschließe.

Selbst innerhalb der Gemeinschaft der Mathematiker war die Idee einer Wahrscheinlichkeitstheorie nicht ganz unumstritten. Zu offensichtlich schien der Widerspruch zwischen der Stochastik als Wissenschaft unsicherer Ereignisse und dem Anspruch der Mathematik als Lehre wahrer Aussagen, unumstößlicher Schlussfolgerungen und gesicherter Erkenntnisse. Beispiel: Entweder hat eine Variable $X$ den Wert fünf, oder sie hat ihn nicht. Im ersten Fall ist die Wahrscheinlichkeit für das Ereignis $X=5$ gleich 1 oder 100 Prozent, ansonsten ist sie 0 Prozent, und für Werte dazwischen schien in der Mathematik kein Platz. Sogar Bertrand Russell, Literaturnobelpreisträger und Vordenker der Philosophie der Mathematik im frühen 20. Jahrhundert (Principia Mathematica, 1910), war dieser Ansicht: „Wie können wir nur von den Gesetzen der Wahrscheinlichkeit sprechen? Ist Wahrscheinlichkeit nicht die Antithese zu jeglichem Gesetz?“[3] Erst die exakte axiomatische Begründung der Stochastik in den Jahren 1901–1933 konnte diesen Widerspruch letztendlich auflösen.

Stochastische Paradoxa

Ein zusätzliches Hindernis bei der Entwicklung der Wahrscheinlichkeitsrechnung war es auch, dass die berechneten Ergebnisse oftmals der menschlichen Intuition zuwiderlaufen. Insbesondere im Zusammenhang mit stochastischer Unabhängigkeit und bedingter Wahrscheinlichkeit treten vielfach Fälle auf, die scheinbar widersprüchliche oder widersinnige Ergebnisse zur Folge haben. Solche Phänomene werden gemeinhin als stochastische Paradoxa bezeichnet, obwohl hier der Begriff des Paradoxons nicht immer zutreffend ist.[4]

Beim Gefangenenparadoxon sind die Personen A, B und C zum Tode verurteilt, jedoch wird einer der drei per Losverfahren begnadigt. Damit ist die Wahrscheinlichkeit für A, zu überleben, gleich ${\frac {1}{3}}$ . Nennt der Gefängniswärter A jedoch nach dem Losvorgang den Namen eines der beiden Mitgefangenen, der nicht begnadigt wird (mindestens eine der beiden anderen Personen wird garantiert hingerichtet), so bleiben nur noch zwei Kandidaten für die Begnadigung übrig und die Überlebenswahrscheinlichkeit für A müsste demnach auf ${\frac {1}{2}}$ steigen. Es ist allerdings kaum vorstellbar, dass diese Information (dass mindestens einer der anderen hingerichtet wird, wusste A schließlich schon vorher) tatsächlich die Chance von A auf eine Begnadigung erhöhen sollte, und in diesem Fall ist es auch nicht so: die Überlebenswahrscheinlichkeit beträgt weiterhin ${\frac {1}{3}}$ . Allerdings ist gleichzeitig die Überlebenswahrscheinlichkeit für den nicht-genannten Mitgefangenen auf ${\frac {2}{3}}$ gestiegen.

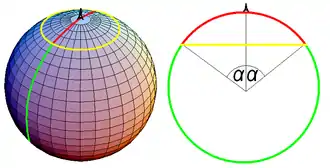
Bertrands Kugelparadoxon: Wie groß ist die Wahrscheinlichkeit, dass der Zufallspunkt oberhalb der gelben Linie (links) landet? Nach Bertrand entspricht sie dem Verhältnis der Länge der roten Linie (rechts) zur Länge des gesamten grünen Großkreises oder α/180°.

Das Kugelparadoxon, auch Bertrand-Paradoxon genannt, wurde 1889 in einem Lehrbuch[5] von Joseph Bertrand aufgestellt. Es lautet: wird ein Punkt zufällig gleichverteilt auf der Oberfläche einer Kugel (etwa der Einschlagpunkt eines Meteoriten auf der Erde) ausgewählt, wie groß ist dann die Wahrscheinlichkeit, dass dieser Punkt von einem vorher fest gewählten Punkt (etwa dem im selben Jahr fertiggestellten Eiffelturm) einen Abstand von weniger als 10 Winkelminuten hat, dass also der Eiffelturm und der Zufallspunkt mit dem Erdmittelpunkt einen Winkel von weniger als ${\frac {10}{60}}$ Grad einschließt? Eine Möglichkeit, diese Wahrscheinlichkeit zu berechnen, besteht darin, die Fläche der in Frage kommenden Punkte (also die Oberfläche der Kappe um den Eiffelturm mit Radius 10 Winkelminuten) durch die Gesamtoberfläche der Kugel zu teilen, was etwa $2{,}1\cdot 10^{-6}$ ergibt. Bertrand schlug aber noch eine zweite Lösung vor: da es für den Abstand irrelevant ist, auf welchem Großkreis durch den Eiffelturm der Punkt liegt und alle Großkreise gleich wahrscheinlich sind, genügt es, exemplarisch einen solchen Großkreis zu betrachten. Dann beträgt die Wahrscheinlichkeit einfach ${\frac {20}{360\cdot 60}}\approx 9{,}2\cdot 10^{-4}$ , da von 360 Grad genau 20 Bogenminuten oder ${\frac {20}{60}}$ Grad in Frage kommen. Bertrands Ansicht nach war keine der beiden Antworten falsch, sondern lediglich die Gleichverteilung auf der Mannigfaltigkeit der Kugeloberfläche nicht wohldefiniert.

Während das Gefangenenparadoxon noch mit verhältnismäßig einfachen stochastischen Hilfsmitteln auflösbar ist, beweist das zweite Problem, dass die Wahrscheinlichkeitstheorie auch zum Ende des 19. Jahrhunderts noch nicht weit genug entwickelt war, um Zufallsphänomene auf einem Kontinuum zweifelsfrei wiederzugeben.

Doch nicht nur die bedingte Wahrscheinlichkeit, die in der ein oder anderen Form der erwähnten Paradoxa eine Rolle spielt, verleitet bisweilen zu Trugschlüssen; auch der Begriff der stochastischen Unabhängigkeit läuft der Intuition oft zuwider. Als Beispiel sei das folgende einfache Spiel genannt: ein gewöhnlicher, sechsseitiger Würfel wird zweimal hintereinander geworfen und die Augenzahlen addiert. Das Spiel ist gewonnen, falls die Summe der Augen eine gerade Zahl ist, andernfalls verliert der Spieler. Nun ist der Ausgang des Spiels (also ob das Ereignis „Spiel gewonnen“ eintritt oder nicht) vom Ausgang des zweiten Wurfs unabhängig. Obwohl sich dieses Ergebnis anhand der Definition der stochastischen Unabhängigkeit leicht nachprüfen lässt, ist es insofern verblüffend, als der zweite Wurf das Spiel ja endgültig entscheidet.

Mögen diese Probleme heute eher wie mathematische Spielereien erscheinen, so darf dabei nicht vernachlässigt werden, dass heute bereits eine voll entwickelte und widerspruchsfreie Wahrscheinlichkeitstheorie zur Verfügung steht. Jedoch mussten erst Begriffe wie Unabhängigkeit und bedingte Wahrscheinlichkeit definiert werden, was schwerfällt, wenn die aus heutiger Sicht einzigen sinnvollen Definitionen zu Trugschlüssen wie den oben erwähnten führen können. Dies mag eine Erklärung dafür sein, dass sich eine konsistente mathematische Wahrscheinlichkeitstheorie nicht bereits früher entwickelte.

Wahrscheinlichkeitsrechnung im Altertum

Ein römischer Astragal

Ein Interesse am Zufall lässt sich bis in die früheste Menschheitsgeschichte zurückverfolgen. Archäologische Funde zeigen an mehreren Stellen auf der ganzen Welt eine auffällige Häufung an Sprunggelenksknöchelchen von Schafen und anderen ähnlich geformten Knochen.[6] Von diesen lateinisch Astragali genannten Knochen ist bekannt, dass sie im römischen Reich als Spielwürfel verwendet wurden – zum Glücksspiel um Geld, aber auch zu rituellen Zwecken, um Auskunft über die Laune der Götter zu erhalten. Solche und ähnliche Orakel, die sich natürlicher (etwa bei der Vogelschau) oder eben künstlicher Zufallsereignisse bedienen, lassen sich weltweit beobachten.

Auffällig ist dabei, dass bereits früh auch Würfel in der heute üblichen Kubusform oder als Tetraeder hergestellt wurden. Einer der frühesten Funde im heutigen Iran datiert etwa auf 3000 v. Chr. Dies bedeutet, dass bereits damals versucht wurde, Wahrscheinlichkeiten gezielt zu beeinflussen, um etwa faire und damit besonders interessante Spiele zu entwerfen. So gesehen kann man den Versuch, ideale Würfel – also solche, bei denen alle Seiten dieselbe Wahrscheinlichkeit aufweisen – zu schaffen, als Frühform stochastischen Kalküls bezeichnen. In Indien waren mindestens seit der vedischen Zeit vor 1000 v. Chr. rituelle und gesellige Spiele bekannt,[7] bei denen fünfseitige Nussfrüchte als Würfel Verwendung fanden, bevor (eingeschränkt ideale) Prismenwürfel entwickelt wurden. In der Geschichte Nala und Damayanti aus dem Epos Mahabharata werden neben Würfelspielen zwei stochastische Themen erwähnt : Zum einen die Kunst des raschen Zählens, eine Art Schluss von einer Stichprobe auf die Gesamtheit[8] sowie ein uns heute unbekannter Zusammenhang zwischen Würfelspielen und dieser Schlussweise.[9][10]

Obwohl das Glücksspiel auch mit idealen Würfeln in der hellenistischen Welt bekannt und verbreitet war und die mathematischen Grundkenntnisse bereits zu Zeiten Euklids oder Pythagoras’ dies durchaus ermöglicht hätten, fand man bisher keine überlieferten Hinweise auf konkrete stochastische Berechnungen aus dieser Zeit. Dies mag zum einen daran liegen, dass der Wahrscheinlichkeitsbegriff damals noch nicht so weit entwickelt war, dass es möglich gewesen wäre, Wahrscheinlichkeit auf einer numerischen Skala einzuordnen, wie es heute üblich ist und im allgemeinen Sprachgebrauch verstanden wird. Es mag aber auch eine Rolle gespielt haben, dass die antike Wissenschaftsphilosophie dem Empirismus stark abgeneigt war. Wahre Erkenntnis könne man nicht aus Experimenten, sondern lediglich aus logischer Argumentation gewinnen. Wahrscheinlichkeit lässt sich hingegen nur im Experiment erfahren und eindeutige Vorhersagen ermöglicht die Stochastik nur im Zusammenhang mit unendlich oft unabhängig wiederholten Vorgängen (etwa beim Gesetz der großen Zahlen), was aber wiederum einen frequentistischen Zugang zum Wahrscheinlichkeitsbegriff voraussetzt. Die in diesem Zusammenhang stehende Aussage von Aristoteles, dass der Zufall sich grundsätzlich der menschlichen Erkenntnis und damit auch der Wissenschaft entziehe, wurde von späteren Aristotelikern zum Dogma erhoben und verhinderte auf längere Zeit die Entstehung einer Wahrscheinlichkeitsrechnung im Abendland.[11]

Früher Fund alter idealer Würfel

Vom römischen Kaiser Claudius (10 v. Chr. – 54 n. Chr.) ist bekannt, dass er ein Freund des Spiels Duodecim Scripta war, eines Vorgängers des heutigen Backgammon, und darüber auch ein Buch verfasste. Da dieses jedoch heute nicht mehr erhalten ist, ist unklar, ob es sich dabei auch um eine stochastische Analyse des Spiels handelte. Es wäre die früheste bekannte Abhandlung dieser Art.

Neben dem Glücksspiel bot auch das Versicherungswesen ein frühes Betätigungsfeld für Wahrscheinlichkeitsabschätzungen. Versicherungsverträge insbesondere für Handelsreisen auf See lassen sich in Babylon und China mindestens bis ins zweite Jahrtausend v. Chr. zurückverfolgen. Beispielsweise werden solche Kontrakte im Codex Hammurapi (etwa 1760 v. Chr.) erwähnt. Im Römischen Reich gab es bereits eine Form von Leibrenten, bei der ein Vertragspartner gegen eine einmalige feste Einzahlung bis zu seinem Lebensende regelmäßige Auszahlungen erhielt. Verschiedene Formen von Krediten und Zinsen lassen sich sogar noch früher feststellen (Codex Ur-Nammu, 3. Jahrtausend v. Chr.) und es kann davon ausgegangen werden, dass solche mit Unsicherheiten behafteten Verträge ähnlich alt sind wie der Handel mit Gütern selbst.

Derartige Versicherungskontrakte sind sicher erst nach rudimentären probabilistischen Überlegungen bezüglich der aus dem Vertrag entstehenden Profite und Verpflichtungen zustande gekommen, bei denen ansatzweise die Wahrscheinlichkeit zukünftiger Ereignisse (etwa der Schiffbruch eines Handlungsreisenden, der frühe Tod eines Leibrentners oder der Ausfall eines Schuldners) geschätzt wurde. Von dieser frühen Form des Risikomanagements sind jedoch kaum Zeugnisse erhalten, was nicht verwunderlich ist, da Kaufleute zu allen Zeiten darauf bedacht waren, ihre Rechenmodelle geheim zu halten.

Mittelalter und frühe Neuzeit

In der christlichen Gesellschaft des Mittelalters waren Orakel und Glücksspiel, obwohl weiterhin verbreitet, doch öffentlich verpönt, sodass eine Forschung über den Zufall zumindest offiziell nicht stattfand, zumal die Wissenschaften zu jener Zeit von Klöstern dominiert wurden. So dauerte es bis ins 13. Jahrhundert, ehe wieder ein Kandidat für die erste stochastische Publikation auftauchte. Das in Hexametern formulierte und anonym veröffentlichte De vetula, heute dem Kanzler der Kathedrale von Amiens, Richard de Fournival (1201–1260), zugeschrieben,[12] beschreibt Spiele mit drei Würfeln und listet explizit die dabei möglichen 216 Kombinationen auf. Das verbotene Thema des Gedichtes mag der Grund für die anonyme Veröffentlichung gewesen sein. Andere Autoren wie der Mönch Jean Buteo (1492–1572, Logistica, um 1560) umgingen das kirchliche Verbot dadurch, dass sie anstatt von Würfeln von „Kombinationsschlössern“ sprachen, deren Schlüssel zum Beispiel 4 Bärte mit jeweils sechs Einstellungen besaßen, um so (6x6x6x6 =) 1296 verschiedene Möglichkeiten darstellen zu können.[13]

Cardanos Liber de Ludo Aleae

Gerolamo Cardano (1501–1576), der erste nachgewiesene Stochastiker

Es dauert bis ins 16. Jahrhundert, ehe die erste nachweisbare stochastische Publikation entstand. Gerolamo Cardano, italienischer Universalgelehrter und einer der einflussreichsten Mathematiker seiner Zeit, legte in seinem ab 1524 entstandenen Werk Liber de Ludo Aleae (das Buch vom Würfelspiel) den Grundstein der Theorie diskreter Zufallsprozesse. Spiele mit bis zu drei Würfeln werden hier (wie zu dieser Zeit üblich fast durchgehend in Prosa) beinahe vollständig besprochen, daneben finden sich aber auch philosophische Gedanken zu Glück (Kapitel XX: De fortuna in Ludo, über das Glück im Spiel), Risikofreude und -scheue (Kapitel XXI: De timore in iactu, über die Furcht vor dem Wurf), Spielsucht (Kapitel IV: Utilitas ludi, & damna, Nutzen und Schaden des Spiels) sowie auch ein eigenes Kapitel über effektive Wege des Betrugs (Kap. XVII: De dolis in huiusmodi Ludis, über die List in so gearteten Spielen). Zusätzlich werden auch Kartenspiele diskutiert, die in Europa ab dem 15. Jahrhundert immer beliebter geworden waren, die aber Cardanos Aufmerksamkeit weitaus weniger erregten als das Hazard, ein wahrscheinlich von Kreuzfahrern aus dem Orient importiertes Würfelspiel.

An einer Veröffentlichung seiner Ergebnisse war Cardano offenbar lange Zeit nicht gelegen, nutzte er doch einen Informationsvorsprung, um regelmäßig mehr zu gewinnen als er einsetzte, und dadurch zum Teil auch sein Studium zu finanzieren. Doch der notorische Spieler verfiel der Spielsucht und verspielte in seinem späteren Leben das meiste seines Vermögens und seines guten Rufes. Sein Buch wurde erst 1663 posthum veröffentlicht, als unlängst andere Gelehrte auf die Wahrscheinlichkeitstheorie aufmerksam geworden waren.

Das Teilungsproblem

Blaise Pascal (1623–1662)

Es sollte bis weit ins 17. Jahrhundert dauern, ehe sich wieder Mathematiker erfolgreich mit dem Zufall beschäftigten, und wie in vielen anderen Wissenschaften hatte sich das Zentrum mittlerweile von Italien nach Frankreich verlegt. Blaise Pascal, einer der einflussreichsten Mathematiker und Religionsphilosophen seiner Zeit, beschrieb am 29. Juli 1654 in einem Brief an seinen Kollegen Pierre de Fermat zwei Probleme, die ihm sein Freund Antoine Gombaud, Chevalier de Méré, zugetragen hatte und die seither als De-Méré- oder Würfelproblem (frz. problème des dés) und Teilungsproblem (problème de partis) bekannt sind:

Das Würfelproblem beschäftigt sich mit einem einfachen Glücksspiel. Die Wahrscheinlichkeit, mit einem Würfel in vier Versuchen mindestens eine Sechs zu werfen, beträgt mit ${\tfrac {671}{1296}}$ knapp mehr als 50 Prozent. Versucht man hingegen, mit zwei Würfeln eine Doppelsechs zu erzielen – wofür die Wahrscheinlichkeit jeweils ${\tfrac {1}{36}}$ , also nur ein Sechstel des Ein-Würfel-Falls beträgt – und macht dafür entsprechend sechsmal so viele, also 24 Würfe, so liegt die Siegchance knapp unter 50 Prozent. Nach de Méré hätte aber die gleiche Wahrscheinlichkeit wie zuvor herauskommen müssen, sodass er einen Rechenfehler vermutete.
Das Teilungsproblem behandelt ein fiktives Spiel, bei dem der Spieler, der zuerst eine festgesetzte Anzahl von fairen Runden für sich entscheidet (bei denen jeder Spieler also je eine Siegchance von 50 Prozent besitzt, unabhängig vom Ausgang der vorangegangenen Runden), einen Geldpreis gewinnt. Das Spiel wird aber durch höhere Gewalt vor der Entscheidung abgebrochen, sodass der Betrag nun abhängig vom derzeitigen Spielstand gerecht geteilt werden soll.

Pierre de Fermat (1607–1665)

Während sich die Partner des Briefwechsels beim ersten Problem schnell einig waren, dass de Mérés „Proportionalitätsansatz“ (sechsmal niedrigere Wahrscheinlichkeit, also sechsmal so viele Versuche für gleiche Siegeschancen) naheliegend, aber falsch sei und demnach kein Widerspruch bestünde, bereitete das zweite größere Schwierigkeiten, da hier die Frage der Gerechtigkeit vage gestellt war und erst sinnvoll mathematisch formuliert werden musste. Letztendlich kamen sie zu dem Entschluss, dass der Einsatz gemäß den Gewinnwahrscheinlichkeiten aufgeteilt werden müsse, und Pascal zeigte auf, wie diese mit Hilfe der Kombinatorik und speziell dem von ihm unlängst entwickelten Pascalschen Dreieck berechnet werden könnten. Die Wahrscheinlichkeit, dass ein Spieler von n ausstehenden Spielen genau k gewinnt, betrage demnach ${\tbinom {n}{k}}\cdot {\tfrac {1}{2^{n}}}$ , wobei der Binomialkoeffizient ${\tbinom {n}{k}}$ dem Pascalschen Dreieck zu entnehmen sei.

Leibniz hatte während seines Parisaufenthalts vom Teilungsproblem gehört und den Nachlass von Pascal eingesehen. Er kannte auch die Schriften von Christiaan Huygens zur Wahrscheinlichkeitsrechnung. 1678 formulierte er in „De incerti aestimatione“ einen eigenen Lösungsvorschlag zum Teilungsproblem. Diese Arbeit existierte nur als Handschrift und wurde erst 1957 veröffentlicht. Leibniz kam zu einem etwas anderen Ergebnis als Pascal und Fermat, obwohl er deren Lösung kannte. Leibniz hatte eine andere Gerechtigkeitsvorstellung als Pascal und Fermat, die heute so interpretiert und in Form eines Leistungsprinzips etwas vereinfacht so ausgedrückt werden kann: „Gleicher Lohn für gleiche Leistung“.[14]

Das Teilungsproblem war bereits vor de Méré bekannt und kann inzwischen bis 1380 zurückverfolgt werden[15] und auch schon Cardano, sowie seine Zeitgenossen Nicolo Tartaglia, Luca Pacioli und Giobattista Francesco Peverone hatten ihrerseits Lösungen angeboten. Die Lösungen von Cardano, Pacioli und Tartaglia unterscheiden sich von Pascals und Fermats aus heutiger Sicht richtigem Vorschlag teilweise stark, da sie mit Mitteln kaufmännischer Gewinn- und Verlustrechnung oder eher wie de Méré mit Proportionen denn kombinatorisch argumentierten. Peverone erhielt fast die nach heutiger Sicht richtige Lösung. Wie sie zustande gekommen ist, kann aber erst erforscht werden, wenn seine Schrift „Due breve e facili trattati“ öffentlich zugänglich gemacht wird. Die italienischen Mathematiker verloren um die Mitte des 16. Jahrhunderts die Überzeugung, dass es eine „richtige“ mathematisch ermittelbare Lösung gibt. Tartaglia äußerte die Meinung, das Problem könne eher juristisch als mit Vernunft gelöst werden.[16] Da Pascal und Fermat von den Bemühungen der Italiener aber nichts gewusst haben dürften, spätere Publikationen jedoch stets auf ihren Überlegungen aufbauten, gilt der Briefwechsel von 1654 vielen als Geburtsstunde der Stochastik.

Niederländische Schule

Christiaan Huygens (1629–1695) führte die Wahrscheinlichkeitsrechnung in den Niederlanden und in England ein

Stand der Briefwechsel von Pascal und Fermat auch am Anfang der Entwicklung modernen stochastischen Kalküls, so wurde dieser doch erst 1679, also nach dem Tod der beiden, veröffentlicht. Damit gebührt die Ehre der frühesten gedruckten stochastischen Publikation dem niederländischen Mathematiker und Physiker Christiaan Huygens, der schon 1655 bei einem Parisaufenthalt vom Diskurs der beiden Franzosen gehört hatte und daraufhin 1657 in Leiden seine Abhandlung De Ratiociniis in Ludo Aleae (Über Schlussfolgerungen im Würfelspiel) veröffentlichte. Huygens Einsicht in die Logik der Spiele und die Frage der Gerechtigkeit derselben geht dabei weit über das hinaus, was Cardano, Pascal und Fermat diskutierten. Auch für unsymmetrische Spiele mit unterschiedlichen Einsätzen oder Gewinnen fand er mit Hilfe eines Indifferenzprinzips (ein Spiel ist demnach gerecht, wenn alle Parteien bereit wären, ihre Rolle mit der der anderen zu tauschen) faire Einsätze und entwickelt dabei einen der bis heute zentralen stochastischen Begriffe: den Erwartungswert. Dadurch ließ sich die Frage nach der Gerechtigkeit auf das einfache Kriterium „erwarteter Gewinn = Einsatz“ reduzieren, womit auch das de-Mérésche Teilungsproblem gelöst war.

Mit den Niederlanden war die Wahrscheinlichkeitsrechnung in einem der Zentren der damaligen Finanzbranche angelangt und hielt dort bald Einzug in die Finanzmathematik. Der Ratspensionär Johan de Witt, eine der einflussreichsten Gestalten in Hollands goldenem Zeitalter und daneben Hobbymathematiker, diskutierte in Waardije van Lijf-renten naer Proportie van Los-renten (der Wert von Leibrenten verglichen mit Amortisationen, 1671) mit Huygens’ Methoden staatliche Leibrenten, die damals Witwen angeboten wurden. Er verwendete dabei das erste bekannte stochastische Mortalitätsmodell und kam zu dem Ergebnis, dass die ausgezahlten Renten aus Sicht des Staates unvernünftig hoch seien. Der Tatsache, dass de Witt als Beamter keine privaten finanziellen Interessen verfolgte, sondern seine Entscheidung der Öffentlichkeit gegenüber rechtfertigen musste, verdankt die Nachwelt wohl die Veröffentlichung seiner Berechnungen. Gerüchten zufolge soll die von ihm veranlasste Rentensenkung auch eine Ursache für einen Volksaufstand im folgenden Jahr gewesen sein, an dessen Ende de Witt gelyncht wurde.

Schisma der Stochastik im 18. und 19. Jahrhundert

Huygens wurde 1663 aufgrund seiner Leistungen auf dem Gebiet der Astronomie als erster Ausländer in die Londoner Royal Society aufgenommen. Nebenbei führte er aber auch die Wahrscheinlichkeitsrechnung in England ein, wo sie auf fruchtbaren Boden traf. Bereits ein Jahr später benutzte John Tillotson, Erzbischof von Canterbury, in On the Wisdom of Being Religious (Über die Weisheit, religiös zu sein) Huygens Erwartungswert, um zu beweisen, dass sich der Glaube an Gott lohne. Sei die Wahrscheinlichkeit, dass Gott tatsächlich existiert, noch so gering, so habe aufgrund des unendlichen Gewinns im Himmel das „Spiel Gottes“ einen unendlich hohen Erwartungswert. Unbeabsichtigterweise machte Tillotson seine Zeitgenossen dadurch auf ein Problem aufmerksam, das die Stochastik noch mehr als zweihundert Jahre lang nicht befriedigend lösen sollte. Wie ist mit Ereignissen umzugehen, deren Wahrscheinlichkeit Null ist? Stichhaltig ist sein Argument nämlich nur dann, wenn man der Existenz Gottes eine positive Wahrscheinlichkeit einräumt. Die Pascalsche Wette zielte auf ähnliche Überlegungen ab.

Erste Fundamentalsätze

Jakob I Bernoulli (1655–1705)

Die Wahrscheinlichkeitsrechnung im 18. Jahrhundert wurde durch zwei bedeutende Werke geprägt, wobei zum ersten Mal eine Abkehr vom Glücksspiel hin zu anderen Anwendungsbereichen deutlich wird. Zum einen erschien 1713 in Basel Ars conjectandi (Die Kunst des Vermutens) von Jakob I Bernoulli, eine unvollendete Abhandlung, die posthum (Bernoulli war bereits 1705 gestorben) aus seinen Tagebüchern veröffentlicht wurde. Aufbauend auf Huygens Vorarbeit finden sich hier bahnbrechende Erkenntnisse auf dem Gebiet der Kombinatorik (beispielsweise taucht hier erstmals der Begriff Permutation auf) und eine vollständige Diskussion der Binomialverteilung, aber es wurden auch erstmals unendliche Folgen von identischen Zufallsprozessen untersucht. Diese sind für den Spezialfall zweier möglichen Ausgänge noch heute als Bernoulli-Ketten bekannt. Die Konvergenz der relativen Häufigkeit gegen die Wahrscheinlichkeit eines Ereignisses wurde von Bernoulli nicht als Axiom vorausgesetzt, sondern in einem Satz geschlossen. Ausgehend davon formulierte er auch die früheste Version des Gesetzes der großen Zahlen, heute einer der zwei wichtigsten Sätze der Stochastik. Eine präzise Definition der Wahrscheinlichkeit blieb aber auch Bernoulli schuldig, er hielt diese aber auch nicht für nötig, da es seines Erachtens keinen Zufall gibt, nur unvollständige Information. Jemand, der um den Lauf der Gestirne nicht weiß, könne demnach auf eine Sonnenfinsternis ebenso wetten wie auf einen Münzwurf.[17] Diese Ansicht macht Bernoulli praktisch zum ersten erklärten Bayesianer. Bemerkenswert ist ferner die Tatsache, dass Bernoullis Hauptinteresse neben den erwähnten Konvergenzaussagen darin bestand, die Stochastik auf die Rechtsprechung anzuwenden, wo es schließlich gilt, aufgrund von unvollständiger Information die Glaubwürdigkeit einer Aussage zu beurteilen (also im bayesschen Sinne die Wahrscheinlichkeit einer wahren Aussage zu bestimmen). Dieser Versuch, mathematisches mit juristischem Schlussfolgern zu versöhnen, wurde allerdings nie ernsthaft praktiziert.

Abraham de Moivre (1667–1754)

Der zweite wesentliche Durchbruch dieser Zeit gelang Abraham de Moivre, einem nach England geflohenen Hugenotten. An der Royal Society veröffentlichte er 1718 The Doctrine of Chances (Die Lehre von der Wahrscheinlichkeit), ein Werk, das die neue englische Schule der Stochastik in den nächsten hundert Jahren wesentlich beeinflussen sollte. Die größte Leistung de Moivres war sicherlich die Formulierung eines zentralen Grenzwertsatzes (neben dem Gesetz der großen Zahlen der zweite fundamentale Satz der Stochastik), heute als Satz von Moivre-Laplace bekannt, und dadurch auch die Einführung der Normalverteilung. Letztere hatte hier allerdings noch nicht den Status einer eigenständigen Wahrscheinlichkeitsverteilung, sondern fungierte lediglich als Grenzwert von diskreten Wahrscheinlichkeiten. Als Hilfsmittel taucht hier erstmals die wahrscheinlichkeitserzeugende Funktion von Verteilungen auf.

Englische Statistiker und französische Probabilisten

Die Arbeiten Bernoullis und de Moivres legten den Grundstein für das, was in den Folgejahren als Theorie der Fehler und später als Statistik bekannt wurde. In den Naturwissenschaften, wo zumeist versucht wird, Gesetzmäßigkeiten zunächst durch Messungen aufzuspüren, kam man immer öfter in Situationen, wo Messungen mit zu großer Ungenauigkeit behaftet waren oder (insbesondere in der Astronomie) nicht beliebig oft wiederholt werden konnten, sodass man dazu übergehen musste, Fehler als Teil des Modells zu verstehen und sie mathematisch zu behandeln. Bernoulli hatte in Ars Conjectandi bereits gezeigt, dass die Wahrscheinlichkeitsrechnung dazu ein geeignetes Werkzeug ist – unabhängig davon, ob man an die zufällige Natur der Fehler glaubt oder nicht.

Der nächste bedeutende Schritt in diese Richtung gelang dem englischen Mathematiker und Pfarrer Thomas Bayes, dessen Hauptwerk An Essay towards solving a Problem in the Doctrine of Chances (Eine Abhandlung zur Lösung eines Problems durch die Wahrscheinlichkeitslehre) 1764 – ebenfalls posthum – veröffentlicht wurde. Darin wird zum einen die bedingte Wahrscheinlichkeit formal eingeführt – bisher war immer stillschweigend von Unabhängigkeit ausgegangen worden –, was in einen Spezialfall des heute sogenannten Satzes von Bayes mündete. Daneben zeigte Bayes als Erster die noch heute gültige Dualität von Stochastik und Statistik auf. Während die Stochastik auf Grundlage von gegebenen Verteilungen auf die Wahrscheinlichkeit zukünftiger Ereignisse zu schließen versucht (bei Bayes: forward probability), ist das Ziel der Statistik, auf Grundlage beobachteter Ereignisse Rückschlüsse auf die ursprüngliche Verteilung zu ziehen (backward probability). Dieses Paradigma legte den Grundstein für die Bayessche Statistik und läutete eine bis heute gültige Vorherrschaft der angelsächsischen Schule auf dem Gebiet der mathematischen Statistik ein (später vertreten durch Francis Galton, William „Student“ Gosset, Karl Pearson, R. A. Fisher oder Jerzy Neyman).

Währenddessen schien die Wahrscheinlichkeitsrechnung in ihrer damaligen Form, die immer noch auf dem Fundament von Pascal und Huygens beruhte, an ihre Grenzen zu stoßen. In immer mehr Anwendungsbereichen wurde es notwendig, sich mit stetigen Verteilungen auseinanderzusetzen, also solchen, die überabzählbar viele Werte annehmen können. Dies schließt aber aus, dass die einzelnen Werte alle mit positiver Wahrscheinlichkeit auftreten, und Ereignisse der Wahrscheinlichkeit null wurden zu jener Zeit als unmöglich interpretiert. Diesen scheinbaren Widerspruch, dass sich Zufallsexperimente aus lauter unmöglichen Ereignissen zusammensetzen sollten, konnten die Mathematiker noch bis ins zwanzigste Jahrhundert nicht völlig schlüssig ausräumen, obwohl sie bereits erste Erfahrungen mit Dichten von Verteilungen machten, soweit es die damalige Integrationstheorie zuließ.

Pierre-Simon Laplace (1749–1827), der wichtigste Vertreter der französischen Schule im 19. Jahrhundert

Derweil wandte sich die Forschung in der von Frankreich dominierten kontinentalen Schule mehr der Erfassung des Wesens von Zufall und Wahrscheinlichkeit zu. Daher verwundert es nicht, dass die wichtigsten Beiträge zu jener Zeit mit Marie Jean Antoine Nicolas Caritat, Marquis de Condorcet (Essai sur l’application de l’analyse à probabilité des décisions (1785), Abhandlung zur Anwendung der Wahrscheinlichkeitsrechnung in Entscheidungen) und Jean Baptiste le Rond d’Alembert (Beiträge über Wahrscheinlichkeit in der Encyclopédie) Autoren hatten, die heute gleichermaßen als Philosophen wie als Mathematiker gelten. Das Hauptwerk aus jener Zeit ist Théorie Analytique des Probabilités (Mathematische Wahrscheinlichkeitstheorie, 1812) von Pierre-Simon Laplace, das einerseits alle bis dahin erzielten Erfolge auf dem Gebiet der Stochastik zusammenfasst, andererseits auch den Versuch einer neuen Philosophie des Zufalls wagt. Laplaces Zugang zur Wahrscheinlichkeit war intuitiv, da er hinter allen Phänomenen eine Gleichverteilung vermutete (siehe Stetige Gleichverteilung, die nicht mit der nach Laplace benannten Laplace-Verteilung zu verwechseln ist). Bisweilen wird der Laplacesche Wahrscheinlichkeitsbegriff auch als autonomer, dritter Zugang neben Frequentismus und Bayesianismus angesehen.[18] Daneben deutete er auch Grenzen der menschlichen Erkenntnis auf dem Gebiet der Naturwissenschaft an (Laplacescher Dämon), womit er von der die letzten Jahrhunderte dominierenden Wissenschaftsphilosophie der Aufklärung zugunsten einer Physik des Zufalls abrückte.

Weitere bedeutende Durchbrüche verzeichneten dieser Jahre Carl Friedrich Gauß und Adrien-Marie Legendre, die 1795 beziehungsweise 1806 unabhängig voneinander die Methode der kleinsten Quadrate auf Grundlage normalverteilter Fehler entwickelten, Siméon Denis Poisson, ein Schüler Laplaces (Poisson-Verteilung), und Pafnuti Lwowitsch Tschebyschow (Tschebyschow-Ungleichung, Verallgemeinerung des Gesetzes der großen Zahlen), der, gefördert vom französischen Mathematiker Joseph Liouville und von Poisson, eine an die französische angelehnte russische Schule begründete. Daneben existierte gegen Ende des 19. Jahrhunderts auch eine wenig einflussreiche deutsche Schule, deren Hauptwerk Principien der Wahrscheinlichkeitsrechnung (1886) von Johannes von Kries die Stochastik mit den Ideen Kants zu vereinen versuchte und dazu eine mathematische Theorie der Spielräume heranzog, die sich aber nach von Kries Tod nicht weiter verbreiten konnte, obgleich von Kries Ideen die späteren Arbeiten Ludwig Wittgensteins beeinflussen sollten.

Axiomatisierung und Grundbegriffe

Die Wahrscheinlichkeitstheorie war gegen Ende des 19. Jahrhunderts unübersehbar in einer Sackgasse angelangt, da die seit Jahrhunderten in Stückarbeit zusammengetragene Theorie den immer komplexeren Ansprüchen der Anwendung nicht mehr gerecht wurde. In der Physik, früher Prototyp deterministischer Wissenschaft, setzte sich etwa vermehrt die Idee durch, Phänomene durch zufällige Prozesse auf molekularer oder atomarer Ebene zu erklären.

Drei eng beieinander liegende Ereignisse um die Jahrhundertwende führten die Stochastik jedoch aus diesem Dilemma heraus hin zu dem strukturellen Rahmen, der heute im engsten Sinne unter Wahrscheinlichkeitstheorie verstanden wird. Das war erstens die Entwicklung der modernen Mengentheorie durch Georg Cantor in den Jahren 1895–1897, die der Analysis einen bis dahin nicht bekannten Grad der Abstraktion erlaubte. Dazu kam zweitens die von David Hilbert auf dem internationalen Mathematikerkongress in Paris vorgestellte Liste von 23 Problemen, deren sechstes sich explizit mit der Axiomatisierung der Wahrscheinlichkeitstheorie und Physik befasste und damit ein breites Spektrum von Mathematikern auf dieses Problem aufmerksam machte. Der dritte und entscheidende Beitrag war die Entwicklung der Maßtheorie durch Émile Borel im Jahr 1901, woraus wenig später die Integrationstheorie nach Henri Léon Lebesgue entstand.

Obwohl es Borel und Lebesgue zunächst nur darum ging, die Integralrechnung konsistent auf Räume wie den $\mathbb {R} ^{n}$ oder allgemeinere Mannigfaltigkeiten auszuweiten, bemerkte man schnell, dass sich diese Theorie geradezu ideal für eine neue Form der Wahrscheinlichkeitsrechnung eignet. Beinahe alle Begriffe der Maßtheorie besitzen eine direkte logische Interpretation in der Stochastik:

Das Grundgerüst der maßtheoretischen Wahrscheinlichkeitstheorie bildet der Wahrscheinlichkeitsraum $(\Omega ,{\mathcal {A}},P)$ . Dabei bezeichnet $\Omega$ in der Integrationstheorie den Definitionsbereich der zu integrierenden Funktionen. Hier ist es die Menge aller elementaren Ereignisse, von denen nur jeweils genau eines gleichzeitig eintreten kann – etwa die sechs Ausgänge „1“, „2“, …, „6“ eines Würfelwurfes.
${\mathcal {A}}$ ist eine σ-Algebra auf $\Omega$ und enthält Teilmengen von $\Omega$ , also aus Elementarereignissen zusammengesetzte Ereignisse (beispielsweise das Ereignis, dass der Würfel eine gerade Augenzahl zeigt, also {2, 4, 6}). Die σ-Algebra (die Bezeichnung geht auf Felix Hausdorff zurück) muss jedoch nicht alle Teilmengen von $\Omega$ enthalten, sondern nur solche, für die eine sinnvolle Wahrscheinlichkeit definiert werden kann.
$P$ ist ein Maß, das jedem Ereignis $A\in {\mathcal {A}}$ eine Wahrscheinlichkeit $P(A)\geq 0$ zuordnet, sodass gewisse Bedingungen erfüllt sind. Da Maße von Borel ursprünglich geometrisch als Verallgemeinerung von Flächeninhalten motiviert waren, wird beispielsweise gefordert, dass die leere Menge das Maß Null hat, also $P(\emptyset )=0$ . In die Sprache der Stochastik übersetzt bedeutet das, dass die Wahrscheinlichkeit, dass keines der in $\Omega$ aufgeführten Ereignisse eintritt, gleich Null ist, $\Omega$ das Experiment also vollständig beschreibt. Des Weiteren wird sinnvollerweise gefordert, dass das Maß (die Fläche) der Vereinigung disjunkter Mengen gleich der Summe der einzelnen Maße (Flächen) ist. Hier bedeutet das, dass falls zwei Ereignisse nie gleichzeitig eintreten können (wie eine gerade und eine ungerade Augenzahl im selben Wurf: die Mengen {1, 3, 5} und {2, 4, 6} sind disjunkt), die Wahrscheinlichkeit dafür, dass eines der beiden auftritt, genau der Summe der einzelnen Wahrscheinlichkeiten entspricht. Das Gleiche wird auch für abzählbare, aber nicht für überabzählbare Vereinigungen gefordert. Der einzige Zusatz, der in der Wahrscheinlichkeitstheorie gegenüber der gewöhnlichen Maßtheorie gemacht werden muss, ist die Normierung des gesamten Raumes auf Wahrscheinlichkeit eins, also $P(\Omega )=1$ .
Mengen, deren Maß Null ist, werden als Nullmengen bezeichnet, wie etwa eine Gerade in der Ebene, die keine Fläche hat. In der Wahrscheinlichkeitstheorie sagt man von Nullmengen, dass sie fast sicher nicht eintreten. Dadurch wird das oben beschriebene Dilemma, dass sich Zufallsexperimente aus lauter unmöglichen Ereignissen zusammensetzen können, aufgelöst. Auch eine Ebene setzt sich aus vielen parallelen Geraden zusammen, von denen jede die Fläche Null hat. Da aber überabzählbar viele Geraden im Spiel sind, entsteht kein Widerspruch zu den von $P$ geforderten Eigenschaften. Dadurch kann erstmals klar zwischen einem Ereignis unterschieden werden, das zwar eintreffen kann, aber Wahrscheinlichkeit Null hat (das ist eine Nullmenge), und einem solchen, das überhaupt nicht eintreten kann (etwa die Augenzahl sieben beim Würfelwurf, die nicht in $\Omega$ enthalten ist).
Lebesgue erweiterte die Maßtheorie um sogenannte messbare Abbildungen. Das sind Funktionen mit Definitionsmenge $\Omega$ , die in gewisser Weise mit der Struktur der σ-Algebra verträglich sind (genaueres dazu siehe unter Maßtheorie), sodass für sie ein Integral definiert werden kann. In der Stochastik sind dies genau die Zufallsvariablen. Dadurch wird die mathematisch unbefriedigende Definition einer Zufallsvariablen als „Variable, die verschiedene Werte mit verschiedener Wahrscheinlichkeit annimmt“ durch eine handfeste mathematische Definition abgelöst.
Das (Lebesgue-)Integral $\textstyle \int _{\Omega }fdP\;$ einer Funktion f bezüglich eines Maßes P ist nichts anderes als der schon zu Huygens Zeiten bekannte Erwartungswert E(f) der Zufallsvariablen.
Misst man die Fläche einer Menge B nicht absolut (das heißt in Relation zu ganz $\Omega$ ), sondern nur relativ zu einer gewissen Teilmenge $A\subset \Omega$ , so entspricht das einfach der bedingten Wahrscheinlichkeit $P(B|A)$ .
Die Unkorreliertheit von Zufallsvariablen, eine abgeschwächte Form der stochastischen Unabhängigkeit, entspricht exakt der Orthogonalität von Funktionen im Lebesgue-Raum $L^{2}(P)$ .

Nachdem die Maßtheorie in den Folgejahren von Borel, Johann Radon (Satz von Radon-Nikodým) und Maurice René Fréchet noch wesentlich abstrahiert und verallgemeinert worden war, war damit beinahe als Nebenprodukt der ideale Rahmen für eine neue Wahrscheinlichkeitstheorie entstanden. In schneller Abfolge wurden in den ersten drei Jahrzehnten des 20. Jahrhunderts alte stochastische Sätze in die neue Wahrscheinlichkeitstheorie übersetzt und neue aufgestellt. Probleme ergaben sich jedoch zunächst bei der Einbettung der bedingten Erwartung in allgemeine Wahrscheinlichkeitsräume und der Frage, ob und wie zu gegebenen (unendlichdimensionalen) Verteilungen auch entsprechende Wahrscheinlichkeitsräume und Zufallsvariablen darauf gefunden werden können, die ebendiese Verteilung besitzen. Die größten Fortschritte auf diesem Gebiet steuerte der junge russische Mathematiker Andrei Kolmogorow bei, ein indirekter Nachkomme der Schule von Tschebyschow und dessen Schüler Andrei Markow (Markow-Ketten, Satz von Gauß-Markow). Vor allem Kolmogorows Konsistenz- oder Erweiterungssatz, der die zweite Frage beantwortet, wurde als entscheidender Durchbruch gefeiert.

Kolmogorows Lehrbuch Grundbegriffe der Wahrscheinlichkeitsrechnung, dessen Erstausgabe im Jahr 1933 erschien, fasste erstmals die gesamte bis dahin entwickelte axiomatische Wahrscheinlichkeitstheorie einschließlich Kolmogorows Erweiterungen lückenlos zusammen und avancierte schnell zum Standardwerk auf diesem Gebiet. Neben seinen eigenen Beiträgen bestand seine größte Leistung darin, alle erfolgversprechenden Ansätze in einem Werk zu bündeln und damit alle verschiedenen stochastischen Schulen – Franzosen, Deutsche, Briten, Frequentisten, Bayesianer, Probabilisten und Statistiker – mit einer einheitlichen Theorie zu versorgen. Deshalb gilt vielen das Jahr 1933 neben dem Jahr 1654 des Pascal-Fermat-Briefwechsels als mögliches Geburtsjahr der Wahrscheinlichkeitsrechnung.

Moderne Wahrscheinlichkeitstheorie

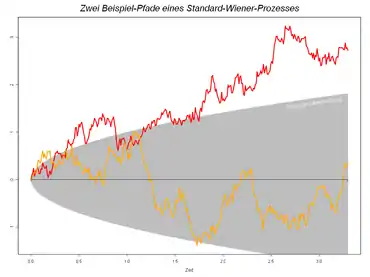
Zwei Pfade einer Brownschen Bewegung.

Nach Festlegung des Kolmogorowschen Axiomensystems konzentrierte man sich in den Folgejahrzehnten in erster Linie auf die Erforschung stochastischer Prozesse, die sich als Zufallsvariablen mit Werten in unendlichdimensionalen (Funktionen-)Räumen auffassen lassen. Eine wichtige Rolle spielte dabei die Brownsche Bewegung. Bereits 1785 von Jan Ingenhousz und später von Robert Brown bei der Beobachtung schwimmender Partikel in Flüssigkeiten beschrieben, wurde dieser Prozess im annus mirabilis 1905 von Albert Einstein verwendet, um die molekulare Struktur von Wasser zu erklären. Dieser damals sehr umstrittene Ansatz verhalf der Stochastik endgültig zum Durchbruch als Hilfsmittel in der Physik. Der Nachweis der Existenz der Brownschen Bewegung als stochastischer Prozess gelang aber erst 1923 dem Amerikaner Norbert Wiener, weshalb die Brownsche Bewegung unter Mathematikern heute auch als Wiener-Prozess und der von Wiener konstruierte Wahrscheinlichkeitsraum als Wiener-Raum bekannt ist. Die Brownsche Bewegung nimmt heute die zentrale Stellung in der stochastischen Analysis ein, doch auch die meisten anderen zu jener Zeit entdeckten Prozesse waren physikalisch motiviert, etwa der Ornstein-Uhlenbeck-Prozess oder das Ehrenfest-Modell.

Zu den am frühesten studierten Klassen von stochastischen Prozessen gehörten die Martingale, welche ursprünglich bereits im 18. Jahrhundert als Roulette-Strategien bekannt waren und nun von Paul Lévy (Lévy-Flüge, Lévy-Verteilung) und Joseph L. Doob (Doob-Meyer-Zerlegung, Doobsche Ungleichungen) in einem neuen Kontext untersucht wurden. Daraus ging später der Begriff der Semimartingale hervor, der heute das Grundgerüst der stochastischen Analysis bildet. Über den Begriff der Martingale wurde zudem eine völlig neue stochastische Interpretation für die σ-Algebra eingeführt, die zuvor bei Borel und Hausdorff nur den Rang eines technischen Hilfsmittels gehabt hatte. Die Menge aller Ereignisse, die zu einem bestimmten Zeitpunkt bekannt sind (bei denen also die Frage, ob sie eintreten, zu diesem Zeitpunkt bereits klar mit ja oder nein beantwortet werden kann), bildet ihrerseits wieder eine σ-Algebra. Deshalb kann mit einer Familie zeitlich angeordneter σ-Algebren, genannt Filtrierung, die zeitliche Informationsstruktur eines Prozesses dargestellt werden. Solche Filtrierungen sind heute ein unerlässliches Hilfsmittel in der stochastischen Analysis.

Eine weitere, bereits früh ausführlich studierte Klasse sind die Lévy-Prozesse, bei denen neben Lévy Alexandr Chintschin (Satz von Lévy-Chintschin, Gesetze des iterierten Logarithmus) die größten Erfolge verzeichneten. Chintschin hatte mit Kolmogorow den Doktorvater geteilt, Lévy mit Fréchet.

Louis Bachelier (1870–1946) gilt heute als erster Vertreter der modernen Finanzmathematik

Nach dem Zweiten Weltkrieg spielte die Finanzmathematik eine immer wichtigere Rolle in der stochastischen Grundlagenforschung. Schon 1900, fünf Jahre vor Einstein, hatte Louis Bachelier in seiner Dissertation Théorie de la Spéculation[19] mit Hilfe einer Brownschen Bewegung Optionspreise an der Pariser Börse zu berechnen versucht, damit allerdings wenig Aufsehen erregt. Ein wichtiger Durchbruch gelang dem Japaner Itō Kiyoshi (Lemma von Itō, Itō-Prozesse), als er in den 1940er Jahren die stochastische Integration begründete, ein in der modernen Finanzmathematik unerlässliches Hilfsmittel, ohne das bahnbrechende Beiträge wie die Entwicklung des Black-Scholes-Modells für Aktienkurse durch Fischer Black, Robert C. Merton und Myron Scholes (Wirtschaftsnobelpreis 1973) nicht möglich gewesen wären. Der Einzug der Brownschen Bewegung in die Finanzmathematik zeigte viele überraschende Parallelen zwischen Physik und Wirtschaftswissenschaften auf: So ist das Problem der Bewertung europäischer Optionen in den Modellen von Bachelier und Black-Scholes gleich dem Problem der Wärmeleitung in homogenen Materialien.

Ein weiteres mathematisches Hilfsmittel, das über die Finanzmathematik Einzug in die Stochastik gehalten hat, ist der Maßwechsel. Ging man zunächst stets von einem festen Wahrscheinlichkeitsmaß aus und konstruierte sich daraufhin stochastische Prozesse, die gewisse Eigenschaften erfüllen (die etwa Martingale sind), so wird nun auch zu bereits definierten Prozessen ein geeignetes Wahrscheinlichkeitsmaß gesucht, sodass der unter dem neuen Maß betrachtete Prozess die gewünschten Eigenschaften erfüllt. Ein zentraler Satz, der den Zusammenhang zwischen der Existenz und Eindeutigkeit gewisser Martingalmaße und der Möglichkeit der Arbitrage auf Aktienmärkten herstellt, ist heute als fundamental theorem of asset pricing (Fundamentalsatz der Aktienbewertung) bekannt.

Literatur

Quellen

Thomas Bayes, An Essay towards solving a problem in the Doctrine of Chance. London, 1763 PDF, 920 kB
Jakob Bernoulli, Ars Conjectandi. Basel, 1713. Übersetzung ins Deutsche von R. Haussner, Oswalds Klassiker der exakten Wissenschaften, Band 107, Leipzig 1899 (Kommentierter Ausschnitt, PDF, 100 kB)
Gerolamo Cardano, Liber de Ludo Aleae. Lyon 1663 (PDF, 1,57 MB)
Christiaan Huygens, De Ratiociniis in Aleae Ludo. Academia Lugduno-Batava (Universität Leiden), 1657 Englische Übersetzung von 1714, PDF, 96 kB
Andrei Kolmogorow, Grundbegriffe der Wahrscheinlichkeitsrechnung. Springer, Berlin 1933, Reprint 1974, ISBN 3-540-06110-X
Pierre-Simon Laplace, Théorie analytique des probabilités. 4. Auflage. Gabay, Paris 1825, Reprint 1995, ISBN 2-87647-161-2

Darstellungen

Rondo Cameron, Larry Neal, A Concise Economic History of the World. Oxford University Press 2002, ISBN 978-0-19-512705-8
Lorraine Daston, Classical Probability in the Enlightenment. Princeton University Press 1988, ISBN 978-0-691-00644-4
Michael Heidelberger, Origins of the logical theory of probability: von Kries, Wittgenstein, Waismann. International Studies in the Philosophy of Science, Band 15, Heft 2, 1. Juli 2001, ISSN 0269-8595 (PDF, 151 kB)
Robert Ineichen, Würfel und Wahrscheinlichkeit – Stochastisches Denken in der Antike, Spektrum Verlag 1996 ISBN 3-8274-0071-6
Ian C. Johnston, And still we evolve. A Handbook for the Early History of Modern Science. Malaspina University-College, British Columbia 1999.
Øystein Ore, Cardano. The gambling scholar. Princeton University Press 1953.
Glenn Shafer, Vladimir Vovk, The origins and legacy of Kolmogorovs Grundbegriffe. Probability and Finance project, Working paper, 2005 (PDF, 544 kB)
Helmut Wirths, Die Geburt der Stochastik. Stochastik in der Schule, Jahrgang 19, Heft 3, Oktober 1999

Weblinks

Einzelnachweise

Shafer/Vovk 2006, S. 12
Daston 1988, S. XV
Simon Singh: Fermats letzter Satz. 11. Auflage. Deutscher Taschenbuch Verlag, München 2006, S. 63 ISBN 978-3-423-33052-7
Gabor J. Szêkely: Paradoxa, Verlag Harri Deutsch, 1990.
Joseph Bertrand: Calcul de probabilités. Gauthier-Villars, Paris 1889
Richard J. Larsen, Morris L. Marx: An Introduction to Mathematical Statistics and its Applications. 3. Auflage. Prentice-Hall, London 2001, S. 3, ISBN 0-13-922303-7
R. Ineichen, S. 15ff
R. Haller, Zur Geschichte der Stochastik, In : Didaktik der Mathematik 16, S. 262–277.
I. Hacking, The emergence of probability. London : Cambridge Press, 1975, S. 7, ISBN 0-521-31803-3
R. Ineichen, S. 19
Wirths 1999, S. 10
Wirths 1999, S. 7.
Barth, Haller: Stochastik LK. Bayer. Schulbuchverlag, 6. Nachdruck der 3. Auflage 1985, S. 71
Wirths 1999, S. 14 und S. 29
Wirths 1999, S. 8.
Wirths 1999, S. 13
Johnston 1999, Section 4, Note 5
Siehe etwa Friedrich Fels: Anmerkungen zum Begriff der Wahrscheinlichkeit aus Praxisorientierter Sicht. Arbeitspapier 51/2000, FH Hannover 2000, ISSN 1436-1035
Englische Übersetzung in Paul Cootner: The Random Character of Stock Market Prices. MIT press, 1967, ISBN 0-262-53004-X

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Shafer/Vovk 2006, S. 12

[2] Daston 1988, S. XV

[3] Simon Singh: Fermats letzter Satz. 11. Auflage. Deutscher Taschenbuch Verlag, München 2006, S. 63 ISBN 978-3-423-33052-7

[4] Gabor J. Szêkely: Paradoxa, Verlag Harri Deutsch, 1990.

[5] Joseph Bertrand: Calcul de probabilités. Gauthier-Villars, Paris 1889

[6] Richard J. Larsen, Morris L. Marx: An Introduction to Mathematical Statistics and its Applications. 3. Auflage. Prentice-Hall, London 2001, S. 3, ISBN 0-13-922303-7

[7] R. Ineichen, S. 15ff

[8] R. Haller, Zur Geschichte der Stochastik, In : Didaktik der Mathematik 16, S. 262–277.

[9] I. Hacking, The emergence of probability. London : Cambridge Press, 1975, S. 7, ISBN 0-521-31803-3

[10] R. Ineichen, S. 19

[11] Wirths 1999, S. 10

[12] Wirths 1999, S. 7.

[13] Barth, Haller: Stochastik LK. Bayer. Schulbuchverlag, 6. Nachdruck der 3. Auflage 1985, S. 71

[14] Wirths 1999, S. 14 und S. 29

[15] Wirths 1999, S. 8.

[16] Wirths 1999, S. 13

[17] Johnston 1999, Section 4, Note 5

[18] Siehe etwa Friedrich Fels: Anmerkungen zum Begriff der Wahrscheinlichkeit aus Praxisorientierter Sicht. Arbeitspapier 51/2000, FH Hannover 2000, ISSN 1436-1035

[19] Englische Übersetzung in Paul Cootner: The Random Character of Stock Market Prices. MIT press, 1967, ISBN 0-262-53004-X