Flächeninhalt
Der Flächeninhalt ist ein Maß für die Größe einer Fläche. Unter Fläche versteht man dabei zweidimensionale Gebilde, das heißt solche, in denen man sich in zwei unabhängige Richtungen bewegen kann. Darunter fallen die üblichen Figuren der ebenen Geometrie wie Rechtecke, Polygone, Kreise, aber auch Begrenzungsflächen dreidimensionaler Körper wie Quader, Kugel, Zylinder usw. Für viele Anwendungen genügen diese Flächen bereits, komplexere Flächen lassen sich oft aus diesen zusammensetzen oder durch diese annähern.
| Physikalische Größe | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Flächeninhalt Oberfläche Querschnittsfläche | ||||||||||||
| Formelzeichen | (area) | ||||||||||||
| Abgeleitet von | Länge | ||||||||||||
| |||||||||||||

Der Flächeninhalt spielt in der Mathematik, bei der Definition vieler physikalischer Größen, aber auch im Alltag eine wichtige Rolle. So ist etwa Druck als Kraft pro Fläche definiert oder das magnetische Moment einer Leiterschleife als Strom mal umflossene Fläche. Grundstücks- und Wohnungsgrößen werden durch Angabe ihrer Grundfläche vergleichbar. Materialverbrauch, beispielsweise von Saatgut für ein Feld oder Farbe zum Anstreichen einer Fläche, kann mit Hilfe des Flächeninhalts abgeschätzt werden.
Der Flächeninhalt ist normiert in dem Sinne, dass das Einheitsquadrat, das heißt das Quadrat mit Seitenlänge 1, den Flächeninhalt 1 hat; in Maßeinheiten ausgedrückt, hat ein Quadrat mit der Seitenlänge 1 m den Flächeninhalt 1 m2. Um Flächen durch ihren Flächeninhalt vergleichbar zu machen, muss man fordern, dass kongruente Flächen denselben Flächeninhalt haben und dass sich der Flächeninhalt zusammengesetzter Flächen als Summe der Inhalte der Teilflächen ergibt.
Die Ausmessung von Flächeninhalten geschieht in der Regel nicht direkt. Stattdessen werden bestimmte Längen gemessen, woraus dann der Flächeninhalt berechnet wird. Zur Messung des Flächeninhalts eines Rechtecks oder einer Kugeloberfläche misst man üblicherweise die Seitenlängen des Rechtecks bzw. den Durchmesser der Kugel und erhält den gewünschten Flächeninhalt mittels geometrischer Formeln, wie sie unten aufgelistet werden.
In der Technik benutzt man zur näherungsweisen Flächenbestimmung mechanische Planimeter, bei denen bei Umfahren der Fläche die Summierung der Flächenelemente kontinuierlich erfolgt. Das Ergebnis kann an einer Skala abgelesen werden. Chemiker pflegten früher den Inhalt einer beliebigen Fläche mit Hilfe einer Analysenwaage oder Mikrowaage zu bestimmen: Die Fläche wurde sorgfältig aus Papier ausgeschnitten und gewogen, ebenso ein Stück des gleichen Papiers mit genau bekannter Fläche; eine Dreisatzrechnung führte zum Ergebnis.
Flächeninhalte einiger geometrischer Figuren
In nachfolgender Tabelle sind einige Figuren aus der ebenen Geometrie zusammen mit Formeln zur Berechnung ihres Flächeninhaltes aufgelistet.
| Figur/Objekt | Flächeninhalt | Bezeichnungen |
|---|---|---|
| Rechteck |  | |
| Dreieck |
|
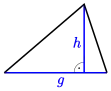 
|
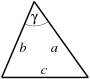
| gleichsch. Dreieck |  | |
| gleichseit. Dreieck |  | |
| Trapez | 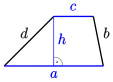 | |
| Raute |  | |
| Parallelogramm | 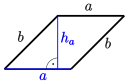 | |
| regul. Sechseck |  | |
| regul. Polygon ( Seiten) |
|
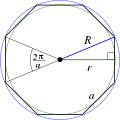 (Umfang) |
| Kreis |  | |
| Ellipse |  | |
| Integral |  | |
| Leibniz-Formel | 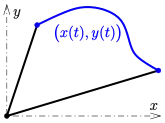 |
Zur Ermittlung des Flächeninhaltes eines Polygons kann man dieses triangulieren, das heißt, es durch Ziehen von Diagonalen in Dreiecke zerlegen, dann die Flächeninhalte der Dreiecke ermitteln und diese Teilflächen schließlich addieren. Sind die Koordinaten , , der Eckpunkte des Polygons in einem kartesischen Koordinatensystem bekannt, kann die Fläche mit der Gaußschen Trapezformel berechnet werden:
Dabei gilt hier für die Indizes: Mit ist und mit ist gemeint. Die Summe ist positiv, wenn die Eckpunkte entsprechend dem Drehsinn des Koordinatensystems durchlaufen werden. Eventuell ist bei negativen Ergebnissen der Betrag zu wählen. Speziell für polygonale Flächen mit Gitterpunkten als Ecken lässt sich der Satz von Pick anwenden. Andere Flächen lassen sich in der Regel leicht durch Polygone approximieren, so dass man leicht an einen Näherungswert kommen kann.
Berechnung einiger Oberflächen
Hier werden exemplarisch einige typische Formeln zur Berechnung von Oberflächen zusammengestellt:
| Figur/Objekt | Oberfläche | Bezeichnungen |
|---|---|---|
| Würfel | 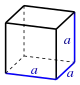 | |
| Quader |  | |
| Tetraeder |  | |
| Kugel (Kugeloberfläche) |
 | |
| Zylinder | 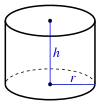 | |
| Kegel |  | |
| Torus |  | |
| Rotationsfläche | (Rotation um x-Achse) |
 |
Ein typisches Vorgehen zur Ermittlung solcher Oberflächen ist das sogenannte „Abrollen“ oder „Abwickeln“ in der Ebene, das heißt man versucht, die Oberfläche derart in die Ebene abzubilden, dass der Flächeninhalt dabei erhalten bleibt, und ermittelt dann den Flächeninhalt der so entstandenen ebenen Figur. Das gelingt aber nicht bei allen Oberflächen, wie das Beispiel der Kugel zeigt. Zur Ermittlung derartiger Oberflächen werden Methoden der Analysis verwendet, beim Beispiel der Kugel kann man etwa Rotationsflächen einsetzen. Oft führt auch die erste Guldinsche Regel zu einem raschen Erfolg, zum Beispiel beim Torus.
Integralrechnung
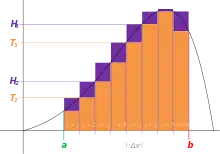
Die Integralrechnung wurde unter anderem zur Ermittlung von Flächeninhalten unter Kurven, das heißt unter Funktionsgraphen, entwickelt. Die Idee besteht darin, die Fläche zwischen Kurve und -Achse durch eine Reihe schmaler Rechtecke zu approximieren und dann die Breite dieser Rechtecke in einem Grenzprozess gegen 0 gehen zu lassen. Die Konvergenz dieses Grenzübergangs hängt von der verwendeten Kurve ab. Betrachtet man einen beschränkten Bereich, etwa die Kurve über einem beschränkten Intervall wie in nebenstehender Zeichnung, so zeigen Sätze der Analysis, dass die Stetigkeit der Kurve bereits ausreicht, um die Konvergenz des Grenzprozesses zu sichern. Dabei tritt das Phänomen auf, dass Flächen unterhalb der -Achse negativ werden, was bei der Bestimmung von Flächeninhalten unerwünscht sein kann. Will man dies vermeiden, muss man zum Betrag der Funktion übergehen.
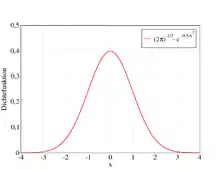
Will man auch die Intervallgrenzen und zulassen, so ermittelt man zunächst die Flächen für endliche Grenzen und wie gerade beschrieben und lässt dann in einem weiteren Grenzprozess , oder beides streben. Hier kann es vorkommen, dass dieser Grenzprozess nicht konvergiert, zum Beispiel bei oszillierenden Funktionen wie der Sinusfunktion. Beschränkt man sich auf Funktionen, die ihren Funktionsgraphen in der oberen Halbebene haben, so können diese Oszillationseffekte zwar nicht mehr auftreten, aber es kommt durchaus vor, dass der Flächeninhalt zwischen Kurve und -Achse unendlich wird. Da die Gesamtfläche eine unendliche Ausdehnung hat, ist das sogar ein plausibles und letztlich auch erwartetes Ergebnis. Wenn die Kurve sich allerdings für weit von 0 entfernte Stellen hinreichend schnell der -Achse nähert, so kann das Phänomen eintreten, dass auch einer unendlich ausgedehnten Fläche ein endlicher Flächeninhalt zukommt. Ein bekanntes und für die Wahrscheinlichkeitstheorie wichtiges Beispiel ist die Fläche zwischen der gaußschen Glockenkurve
und der -Achse. Obwohl die Fläche von bis reicht, ist der Flächeninhalt gleich 1.
Bei dem Versuch, weitere Flächen, etwa auch unter unstetigen Kurven, zu berechnen, stößt man schließlich auf die Frage, welchen Mengen in der Ebene denn überhaupt ein sinnvoller Flächeninhalt zukommen soll. Diese Frage erweist sich als schwierig, wie im Artikel zum Maßproblem ausgeführt wird. Es stellt sich heraus, dass der hier verwendete intuitive Flächeninhaltsbegriff nicht sinnvoll auf alle Teilmengen der Ebene ausgedehnt werden kann.
Differentialgeometrie
In der Differentialgeometrie wird der Flächeninhalt einer ebenen oder gekrümmten Fläche mit den Koordinaten als Flächenintegral berechnet:
Dabei entspricht das Flächenelement der Intervallbreite in der eindimensionalen Integralrechnung. Es gibt den Flächeninhalt des durch die Tangenten an die Koordinatenlinien aufgespannten Parallelogramms mit den Seitenlängen und an. Das Flächenelement ist abhängig vom Koordinatensystem und der Gaußschen Krümmung der Fläche.
In kartesischen Koordinaten ist das Flächenelement . Auf der Kugeloberfläche mit dem Radius und der Länge sowie der Breite als Koordinatenparametern gilt . Für die Oberfläche einer Kugel () erhält man damit den Flächeninhalt:
Zur Berechnung des Flächenelements ist es nicht zwingend erforderlich, die Lage einer räumlichen Fläche im Raum zu kennen. Das Flächenelement kann allein aus solchen Maßen abgeleitet werden, die innerhalb der Fläche gemessen werden können, und zählt damit zur inneren Geometrie der Fläche. Dies ist auch der Grund dafür, dass sich der Flächeninhalt einer (abwickelbaren) Fläche beim Abwickeln nicht ändert und damit durch Abwickeln in eine Ebene bestimmt werden kann.
Flächen in der Physik
Flächen treten naturgemäß auch in der Physik als zu messende Größe auf. Flächen werden in der Regel indirekt unter Verwendung obiger Formeln gemessen. Typische Größen, bei denen Flächen auftreten, sind:
- Druck = Kraft pro Fläche
- Intensität = Energie pro Zeit und Fläche
- Magnetisches Moment einer Leiterschleife = Strom mal umflossene Fläche
- Oberflächenspannung = Zur Flächenvergrößerung geleistete Arbeit pro zusätzlich entstandene Fläche
- Oberflächenladungsdichte = Ladung pro Fläche
- Stromdichte = Strom pro durchflossene Fläche
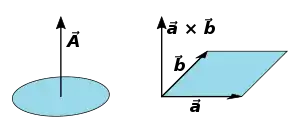
Oft wird der Fläche auch eine Richtung, die senkrecht zur Fläche verläuft, zugewiesen, was die Fläche zu einem Vektor macht und ihr wegen der zwei möglichen Wahlen der senkrechten Richtung eine Orientierung verleiht. Die Länge des Vektors ist dabei ein Maß für den Flächeninhalt. Bei einem durch Vektoren und begrenzten Parallelogramm ist dieser das Vektorprodukt
- .
Sind es Oberflächen, verwendet man in der Regel das Normalenvektorfeld, um ihnen an jeder Stelle lokal eine Richtung zuweisen zu können. Dies führt zu Fluss-Größen, die man als Skalarprodukt aus betrachtetem Vektorfeld und Fläche (als Vektor) definiert. So errechnet sich der Strom aus der Stromdichte gemäß
- ,
wobei im Integral das Skalarprodukt
gebildet wird. Zur Auswertung derartiger Integrale sind Formeln zur Berechnung von Oberflächen hilfreich.
Es treten in der Physik daneben auch Flächengrößen auf, die tatsächlich experimentell bestimmt werden, etwa Streuquerschnitte. Hierbei geht man von der Vorstellung aus, ein Teilchenstrom treffe auf ein festes Zielobjekt, auf das sogenannte Target, und die Teilchen des Teilchenstroms treffen mit gewisser Wahrscheinlichkeit auf die Teilchen des Targets. Das makroskopisch gemessene Streuverhalten lässt dann Rückschlüsse auf die Querschnittsflächen zu, welche die Targetteilchen den Stromteilchen entgegenhalten. Die so ermittelte Größe hat die Dimension einer Fläche. Da das Streuverhalten nicht nur von geometrischen Größen, sondern auch von anderen Wechselwirkungen der Streupartner untereinander abhängt, ist die gemessene Fläche nicht immer direkt mit dem geometrischen Querschnitt der Streupartner gleichzusetzen. Man spricht dann allgemeiner vom Wirkungsquerschnitt, der ebenfalls die Dimension einer Fläche hat.
Flächenberechnung im Vermessungswesen
Flächeninhalte von Grundstücken, Grundstücksteilen, Ländern oder anderen Gebieten können in der Regel nicht mit den Formeln für einfache geometrische Figuren ermittelt werden. Solche Flächeninhalte lassen sich graphisch, halbgraphisch, aus Feldmaßen oder aus Koordinaten berechnen.[1]
Bei den graphischen Verfahren muss eine Kartierung der Fläche vorliegen. Flächen, deren Grenzen durch ein Polygon gebildet werden, können in Dreiecke oder Trapeze zerlegt werden, deren Grundlinien und Höhen gemessen werden. Aus diesen Maßen werden dann die Flächeninhalte der Teilflächen und schließlich der Flächeninhalt der Gesamtfläche berechnet. Die halbgraphische Flächenberechnung wird angewendet, wenn die Fläche in schmale Dreiecke zerlegt werden kann, deren kurze Grundseite im Felde genau gemessen wurde. Da der relative Fehler des Flächeninhalts hauptsächlich durch den relativen Fehler der kurzen Grundseite bestimmt wird, kann durch die Messung der Grundseite im Felde statt in der Karte die Genauigkeit des Flächeninhalts gegenüber der rein graphischen Methode gesteigert werden.
Unregelmäßige Flächen lassen sich mit Hilfe einer Quadratglastafel erfassen. Diese trägt auf der Unterseite ein Gitter aus Quadraten, deren Seitenlänge bekannt ist (z. B. 1 Millimeter). Die Tafel wird auf die kartierte Fläche gelegt und der Flächeninhalt durch Auszählen der Quadrate, die innerhalb der Fläche liegen, ermittelt.
Bei langgestreckten Flächen kann eine Planimeterharfe eingesetzt werden. Diese besteht aus einem Blatt mit parallelen Linien, deren einheitlicher Abstand bekannt ist. Die Planimeterharfe wird so auf die Fläche gelegt, dass die Linien etwa senkrecht zur Längsrichtung der Fläche stehen. Dadurch wird die Fläche in Trapeze unterteilt, deren Mittellinien mit einem Stechzirkel addiert werden. Aus der Summe der Längen der Mittellinien und dem Linienabstand kann der Flächeninhalt berechnet werden.

Besonders bei Flächen mit krummliniger Begrenzung eignet sich das Planimeter, ein mechanisches Integrationsinstrument, zur Ermittlung des Flächeninhalts. Mit dem Fahrstift des Planimeters muss die Begrenzung abgefahren werden. Beim Umfahren der Fläche dreht sich eine Rolle und an einem mechanischen oder elektronischen Zählwerk können die Drehung der Rolle und die Größe der Fläche abgelesen werden. Die Genauigkeit hängt davon ab, wie genau der Bearbeiter mit dem Fahrstift den Flächenrand abfährt. Das Ergebnis ist umso genauer, je kleiner der Umfang im Verhältnis zum Flächeninhalt ist.
Die Flächenberechnung aus Feldmaßen kann angewendet werden, wenn sich die Fläche in Dreiecke und Trapeze zerlegen lässt und die zur Flächenberechnung benötigten Strecken im Felde gemessen sind. Wenn die Eckpunkte der Fläche im Orthogonalverfahren auf eine Messungslinie aufgewinkelt wurden, kann die Fläche auch mit der Gaußschen Trapezformel berechnet werden.
Heute werden Flächeninhalte häufig aus Koordinaten berechnet. Dies können beispielsweise die Koordinaten von Grenzpunkten im Liegenschaftskataster oder Eckpunkte einer Fläche in einem Geoinformationssystem sein. Oft sind die Eckpunkte durch gerade Linien, gelegentlich auch durch Kreisbögen verbunden. Daher kann der Flächeninhalt mit der Gaußschen Trapezformel berechnet werden. Bei Kreisbögen sind die Kreissegmente zwischen Polygonseite und Kreisbogen zu berücksichtigen. Ist in einem Geoinformationssystem der Inhalt einer unregelmäßigeren Fläche zu ermitteln, kann die Fläche durch ein Polygon mit kurzen Seitenlängen approximiert werden.
Siehe auch
Einzelnachweise
- Heribert Kahmen: Vermessungskunde I. Walter de Gruyter, Berlin 1988.
Weblinks
- Umrechnung: Rundes Kabel, Draht und Leitung – Durchmesser in Kreis-Querschnitt und Querschnitt in Durchmesser
- Eric W. Weisstein: Area. In: MathWorld (englisch).