Fehlschluss
Als Fehlschluss oder Trugschluss – lateinisch fallacia – bezeichnet man in der philosophischen Logik eine Schlussfolgerung, bei der die abgeleitete Aussage nicht aus den explizit angegebenen oder den implizit angenommenen Voraussetzungen folgt.
Das bedeutet nicht unbedingt, dass die abgeleitete Aussage auch falsch ist: Ein Fehlschluss bietet bloß keinen Aufschluss über den tatsächlichen Wahrheitsgehalt der abgeleiteten Aussage.
Im Argumentschema der Begriffslogik wird auch der Ausdruck Paralogismus für Fehlschlüsse verwendet. Ein Fehlschluss beruht auf einem Irrtum in der Anwendung von Schlussregeln; er ist nach den Regeln einer formalen Logik nicht korrekt. Gelegentlich werden aber auch formal gültige Schlüsse aus falschen Voraussetzungen als Fehlschlüsse bezeichnet.
Klassifizierung von Fehlschlüssen
Ein mit Absicht herbeigeführter Fehlschluss wird auch als Fangschluss, Scheinargument oder als Sophismus bezeichnet, ein unbeabsichtigter Fehlschluss wird auch Paralogismus genannt. Unbeabsichtigte Fehlschlüsse können psychologisch als Folge von bestimmten kognitiven Verzerrungen (engl. bias) erklärt werden oder durch Urteilsheuristiken, die in Sonderfällen nicht zum richtigen Ergebnis führen. Neben der Logik beschäftigt sich die Sozialpsychologie und die Denk- und Kognitionspsychologie mit Fehlschlüssen. Auch aus der Rhetorik sind umfangreiche Listen von Fehlschlüssen und Scheinargumenten bekannt.
Seit der Antike werden verschiedene Arten von Fehlschlüssen untersucht, etwa in Aristoteles’ Sophistischen Widerlegungen oder in den Texten der älteren Stoa. Moderne Klassiker, die Fehlschlüsse rhetorisch und philosophisch betrachten, sind Schopenhauers Eristische Dialektik[1] und das für den englischen Sprachraum maßgebliche System der deduktiven und der induktiven Logik[2] John Stuart Mills.
Seit der Entwicklung der klassischen formalen Logik beschäftigt sich die philosophische Logik deutlich seltener damit, Fehlschlüsse aufzulisten, zu klassifizieren und zu systematisieren. Stattdessen werden besonders in der Analytischen Philosophie einzelne Fehlschlüsse formalsprachlich rekonstruiert. Die Übersetzung in eine formale Sprache soll aufzeigen, wo der Fehlschluss einen Ableitungsschritt macht, der gegen die formalen Schlussregeln verstößt.
Ein berühmter Fehlschluss in der Philosophie ist der naturalistische Fehlschluss, bei dem es nach einer Lesart um die Frage geht, ob man von deskriptiven auf normative Aussagen, vom Sein auf das Sollen schließen darf. Philosophisch bedeutsam ist auch der intensionale Fehlschluss, der darauf beruht, dass in sogenannten intensionalen Kontexten (A glaubt, meint, weiß etc.) Ausdrücke, obwohl sie dasselbe bezeichnen, nicht ohne weiteres ausgetauscht werden dürfen.
Die folgende Aufzählung von Typen und Beispielen kann weder Vollständigkeit noch eine klare Systematik beanspruchen, da ein solcher Anspruch eine spezifische Theorie der Logik voraussetzen würde.
Mathematische Scheinbeweise
In der Mathematik entstehen Fehlschlüsse durch falsche Anwendung von Rechenregeln. Bekannt sind z. B. Scherzbeweise, die auf versteckter Division durch Null beruhen.
| Beispiele |
|---|
|
Die Gleichung ist eine wahre Aussage. Dividiert man beide Seiten durch und ignoriert dabei, dass dies in üblichen Rechensystemen kein weiterverwendbares Ergebnis liefert, so erhält man die falsche Aussage . Oft wird die Division durch Null verschleiert, indem statt z. B. der Faktor verwendet wird. |
Verwechslung von Begründung und Korrelation
Von einer Korrelation, dem gemeinsamen Auftreten zweier Sachverhalte (z. B. zeitlich oder statistisch, innerhalb einer Stichprobe), wird fälschlich auf ein Begründungsverhältnis geschlossen. Solche Schlüsse sind keine deduktiven oder zwingenden Schlussfolgerungen und keine wahrheitskonservierenden logischen Operationen: Aus wahren Prämissen kann kein falscher Schlusssatz hergeleitet werden. Im besten Fall kann die Verknüpfung zweier Tatsachen eine Hypothese über einen Zusammenhang liefern, die mit wissenschaftlichen Methoden weiter geprüft werden muss. Wenn man das Aufstellen einer solchen Hypothese als logisches Schlussfolgern ansieht, so spricht man von einer Abduktion. Für die übliche Logik ist der Begriff der Schlussfolgerung allerdings auf wahrheitskonservierende Operationen eingeschränkt.
Zeitlicher Zusammenhang von Ereignissen
Cum hoc, ergo propter hoc (lat. ‚mit diesem, also deswegen‘) bezeichnet einen logischen Fehler, bei dem zwei immer gemeinsam aufgetretene Ereignisse als Ursache und Wirkung erklärt werden. Auch der Sonderfall post hoc, ergo propter hoc (lat.: ‚danach, also deswegen‘) – das Ereignis A erfolgt zeitlich vor B – beweist keine Kausalität: Der Tag folgt stets auf die Nacht, aber nicht, weil diese die Ursache für jenen ist. Möglicherweise ist A eine notwendige, aber keine hinreichende Bedingung von B. Inwieweit Post hoc, ergo propter hoc gilt, war Gegenstand der Untersuchungen von David Hume und Immanuel Kant. Während Hume bestreitet, dass per post hoc, ergo propter hoc aus der Erfahrung Regeln gewonnen werden können, die mehr zum Ausdruck bringen als eine wiederholte Beobachtung und dadurch entstandene gedankliche Assoziation, darf laut Kant unter Berufung auf allgemeine Gesetze a priori eine Naturkausalität behauptet werden. Ein bekanntes Beispiel für dieses Problem betrifft die Übertragung kinetischer Energie: Wenn etwa eine Billardkugel eine andere trifft, so sieht ein Beobachter nichts als den zeitlichen Zusammenhang zwischen Auftreffen der ersten und Geschwindigkeitsänderung der zweiten. Die Übertragung der kinetischen Energie von einer Kugel auf die andere ist nicht beobachtbar, sondern nur die Geschwindigkeiten der Kugeln vor und nach dem Zusammenprall. Unter Einbeziehung der Newton’schen Gesetze der Bewegung aber muss hier sogar eine Kausalität angenommen werden.
Räumlicher Zusammenhang von Ereignissen
Dies ist die räumliche Variante von Cum hoc ergo propter hoc: Aus der räumlichen Nähe zweier Ereignisse wird (logisch falsch, aber plausibel) auf eine Ursache für diese Nähe geschlossen. So wählte Peirce folgendes Beispiel für eine Abduktion (siehe auch Beweis im schwachen Sinn):[3] Jemand findet einige weiße Bohnen und daneben einen Sack voller weißer Bohnen. Er schließt:
| Diese Bohnen sind weiß. | |
| Alle Bohnen in diesem Sack sind weiß. | |
| Abduktion: | Diese Bohnen stammen aus diesem Sack. |
Die gefolgerte Hypothese ist plausibel, aber nicht zwingend.
In der Gestaltpsychologie ist das Gesetz der Nähe bekannt: Elemente mit geringen Abständen voneinander werden als zusammengehörig wahrgenommen. Wird diese Zusammengehörigkeit als Unterordnungs- oder Kausalverhältnis interpretiert, so kommt es zu einem Fehlschluss.
Irrelevante Bezugsgröße
Ein verbreiteter Fehlschluss schließt von der Häufigkeit des Auftretens einer Eigenschaft F unter der Bedingung G in einer statistischen Erhebung darauf, dass das Vorliegen von F in Einzelfällen ein relevanter Indikator für G ist. Dabei wird jedoch oft eine falsche oder unpassende Bezugsgröße gewählt, so dass ein Prävalenzfehler auftritt. Liegt G zeitlich nach F und wird die statistische Korrelation als Kausalrelation interpretiert (etwa im Sinne einer hinreichenden, aber nicht notwendigen Bedingung), so handelt es sich um einen Sonderfall von post hoc, ergo propter hoc.
So wird beispielsweise gelegentlich vor Cannabis als Einstiegsdroge für Heroin gewarnt. Zwischen beiden Konsumentengruppen gibt es eine tatsächliche Überschneidung: Laut statistischen Erhebungen waren die meisten Heroinbenutzer (H) zuvor Cannabiskonsumenten (C). Daraus folgt jedoch nicht, dass Cannabiskonsum zur Heroinabhängigkeit führt: Tatsächlich hat die Mehrheit der Cannabisbenutzer kein Interesse an Heroin. So verweist Entscheidungstheoretiker Gerd Gigerenzer darauf, dass es, auch wenn die Aussage „Die meisten Heroinbenutzer waren früher Cannabisbenutzer“ stimmt, falsch wäre, daraus zu folgern „Die meisten Cannabisbenutzer werden Heroinbenutzer sein“.[4]
Da in diesem Beispiel eine bedingte Wahrscheinlichkeit mit ihrer Umkehrung gleichgesetzt wird, spricht man hier auch von Confusion of the Inverse.
Klapperstorch
| Im Frühjahr kehren die Störche nach Europa zurück. | |
| Im Frühjahr steigt in Europa die Geburtenzahl. | |
| Fehlschluss: | Die Rückkehr der Störche verursacht eine Steigerung der Geburtenzahl. |
Unter Beachtung der wirklichen Ursache für Geburten handelt es sich klar um einen Fehlschluss. Wird er naiv getroffen, handelt es sich um einen Paralogismus; wird er jedoch vorgebracht, um jemanden zu überzeugen, dass die Kinder vom Storch gebracht werden, handelt es sich um einen Sophismus.
Schnelldiagnose
| Patient XY hat Rückenschmerzen. | |
| Patient XY hat einen Bandscheibenvorfall. | |
| Fehlschluss: | Der Bandscheibenvorfall ist die Ursache für die Rückenschmerzen. |
Es handelt sich sogar dann um einen Fehlschluss, wenn die Konklusion wahr ist: Medizinisch ist es gut möglich, dass die Rückenschmerzen andere Ursachen haben, und es sollten weitere Untersuchungen vorgenommen werden, um sie auszuschließen. Wegen der naheliegenden möglichen Erklärung kommt es zu einer Fehlanwendung von Ockhams Rasiermesser. Dieser Fehlschluss lässt sich aber auch als einfachster Sonderfall einer falschen Disjunktion verstehen.
Syllogistische Fehlschlüsse
In der Tradition der Logik wurden nicht nur die gültigen Schlussfolgerungen untersucht, sondern auch logische Fehlschlüsse im Rahmen der bis Ende des 19. Jahrhunderts üblichen Syllogistik betrachtet und kategorisiert.
Quaternio Terminorum
(lat. Vierheit der Begriffe) Im kategorischen Syllogismus müssen genau drei verschiedene Begriffe vorkommen: Der Oberbegriff als Prädikat in Obersatz und Konklusion, der Mittelbegriff als Subjekt im Obersatz und als Prädikat im Untersatz und der Unterbegriff als Subjekt in Untersatz und Konklusion. Bei der quaternio terminorum treten jedoch zwei verschiedene Mittelbegriffe auf, wodurch der Schluss, ungeachtet der Wahrheit der Prämissen und der Konklusion, ungültig wird:
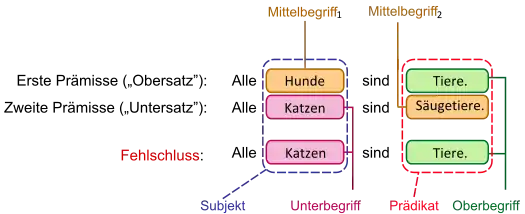
Quaternio-Terminorum-Fehlschlüsse sind selten so offensichtlich wie in dem Beispiel, da die Verschiedenheit der Begriffe oft durch eine echte oder durch Formalisierung entstandene Homonymie verborgen ist. Eine quaternio terminorum durch Homonymie verletzt die Form des Syllogismus, indem in Ober- und Untersatz an die Stelle des Mittelbegriffs ein mehrdeutiger Ausdruck gesetzt wird, der in einer Bedeutung den Obersatz, in einer anderen den Untersatz zu einer wahren Aussage macht. Ein Fehlschluss ist die Folge, da mit der alternativen Bedeutung des Ausdrucks in der Position des Mittelbegriffs ein vierter Begriff eingeführt wurde. Neben der Homonymie kann auch eine Amphibolie Ursache der Täuschung sein, oder eine Metábasis eis állo génos, also eine grammatische Vieldeutigkeit oder ein Wechsel des Bezugssystems der Begriffe. Die bewusste Verwendung wird auch als Erschleichung oder Subreption bezeichnet (Siehe auch: Fallacia falsi medii Falsche Disjunktion).
Echte Homonymie
Leicht zu entdecken ist die Homonymie in folgendem Beispiel:
| Was einen Bart hat, kann man rasieren. | |
| Schlüssel haben einen Bart. | |
| Fehlschluss: | Schlüssel kann man rasieren. |
(Schlüsselbart und Barthaar)
Homonymie durch Formalisierung
Komplexer ist folgendes Beispiel:
| Alle Eltern lieben ihre Kinder. | |
| Alle Kinder lieben Schokolade. | |
| Fehlschluss: | Alle Eltern lieben Schokolade. |
Wenn man die Wahrheit der Prämissen zugesteht, kommt dennoch ein Fehlschluss zustande, weil fälschlicherweise die Relation „x liebt y“ für das Prädikat gehalten wird. Für syllogistische Schlüsse sind aber nur einstellige Begriffe als Prädikate zulässig („x liebt Schokolade“, „x liebt ihre Kinder“). In diesem Syllogismus kommen also vier Begriffe vor, wenn die Prämissen syllogistisch formalisiert werden.
| Je mehr Gutes man tut, desto besser ist es. | |
| Die Arznei einzunehmen tut dem Kranken gut. | |
| Fehlschluss: | Je mehr Arznei man einnimmt, desto besser ist es. |
Das Problem dieses Schlusses ist nicht nur die Fragwürdigkeit der ersten Prämisse. Tatsächlich ist die Arznei nur unter der Bedingung hilfreich, dass man krank ist, und es wird auch in der zweiten Prämisse gar nicht über die Menge der Arznei quantifiziert, wie es die Konklusion tut. Tatsächlich gibt es Medikamente, die bei Überdosierung schädlich sind. Ein klügerer Schluss, der die Verwechslung von Guter Tat und einzelner Arzneidosis vermeidet, käme vielleicht zu dem Ergebnis: „Je mehr Kranken man eine Arznei gibt, desto besser“.
Klassische Fehlschlüsse nach Eubulides
Die Sophismen des Eubulides haben das Ziel, einen Gesprächspartner in seiner Gewissheit zu erschüttern oder vor einem Publikum zu diskreditieren, indem sie ihn dazu bringen, etwas Paradoxes zuzugeben.
| Was du nicht verloren hast, das hast du noch. | |
| Hörner hast du nicht verloren. | |
| Fehlschluss: | Du hast also Hörner. |
| Weißt du, wer dieser Verhüllte ist? – Nein! | |
| Es ist Dein Vater! | |
| Fehlschluss: | Du weißt nicht, wer dein Vater ist. |
Fehler der logischen Distribution
Wenn im Schlusssatz eines Syllogismus das syllogistische Subjekt distribuiert ist, das heißt, wenn über alle Mitglieder der vom Subjekt bezeichneten Klasse ein Urteil gefällt wird (z. B. „Alle S sind P“, „Keine S sind P“), dann muss auch der Untersatz (2. Prämisse, in der das Subjekt der Konklusion eingeführt wird) ein Urteil über alle Klassen-Mitglieder sein. In diesen Urteilen gilt das Prädikat bzw. der Mittelbegriff für jeden einzelnen Gegenstand, der unter den Subjektbegriff fällt, das Prädikat wird verteilt (distribuiert).
Nicht distribuiertes Subjekt
Fehlschlüsse entstehen, wenn in der zweiten Prämisse nur eine Teilmenge des Subjekts gemeint ist, die Konklusion sich aber auf alle Elemente der Kategorie bezieht. Zwei Beispiele:
| Alle Vegetarier sind gesund. | |
| Einige Menschen sind Vegetarier. | |
| Fehlschluss: | Alle Menschen sind gesund. |
Hier ist der Fehlschluss leicht zu entdecken. Komplizierter ist das folgende Beispiel:
| Omnivoren essen Fleisch. | |
| Menschen sind Omnivoren. | |
| Fehlschluss: | Alle Menschen essen Fleisch. |
Während im Schlusssatz jeder einzelne lebende Mensch im Besonderen gemeint ist (distributiv), sind die „Menschen“ im Untersatz allgemein die Vertreter des biologischen Gattungsbegriffes (kollektiv). Ebenso im Obersatz: Als Kollektiv kommt es den Omnivoren zu, dass sie Fleisch essen. Für den einzelnen Omnivoren ist damit nicht gesagt, dass er je Fleisch gegessen hat, sondern dass er zu einer Gattung gehört, die eine „Veranlagung“ dazu besitzt bzw. Fleisch verdauen kann.
Nicht distribuierter Mittelbegriff
Auch: Sophismus des kollektiven Mittelbegriffs (lat. non distributivi, sed collectivi medii)
In einem gültigen Syllogismus ist der Mittelbegriff in mindestens einer Prämisse distribuiert. Ist er es nicht, kann ein Fehlschluss wie der folgende auftreten:
| Alle Menschen sind Zweibeiner. | |
| Einige Zweibeiner sind Vögel. | |
| Fehlschluss: | Einige Menschen sind Vögel. |
Hier wird im Untersatz „x ist ein Vogel“ nicht über alle Zweibeiner distribuiert.
Falsche Disjunktion
Auch in Disjunktiven Syllogismus sind Fehlschlüsse im Sinne einer Erschleichung möglich, bei der das Verhältnis zwischen dem Mittelbegriff und den anderen Begriffen bei näherer Betrachtung nicht den Anforderungen des syllogistischen Schließens genügt. Dabei handelt es sich um die sogenannte Falsche Disjunktion (siehe dort).
Fehlschlüsse in der Kriminalistik
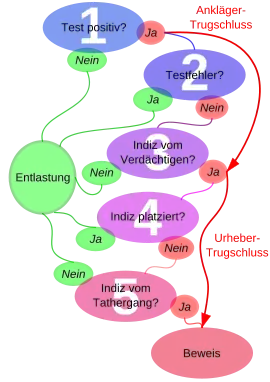
Das Ergebnis einer DNA-Analyse, eines Fingerabdrucks oder einer sonstigen Spur alleine kann nicht über Schuld oder Nichtschuld eines Verdächtigen entscheiden. Es wird nur als Indiz gewertet, das durch weitere ergänzt werden muss. Viele Verdächtige legen allerdings ein Geständnis ab, wenn man sie mit dem Ergebnis konfrontiert. Ist das nicht der Fall, muss das Ergebnis interpretiert werden, wobei Fehlschlüsse nicht auszuschließen sind. Im Folgenden wird der Spezialfall eines DNA-Tests betrachtet, die Mechanismen lassen sich aber auch auf andere Arten von Spuren übertragen. Ein ungültiger Schritt macht die gesamte Schlusskette ungültig:
- DNA-Test ergibt keine Übereinstimmung.
- Falsche Übereinstimmung durch falsch positive Testergebnisse.
- Zufällige Übereinstimmung. Der Verdächtigte muss nicht der Urheber der Spur sein, nur weil eine Übereinstimmung vorliegt.
- Das biologische Material kann von jemand anderem hinterlegt worden sein.
- Das biologische Material muss nicht zum Tatzeitpunkt hinterlegt worden sein.
Der Trugschluss des Anklägers (engl. prosecutor’s fallacy)[5] besteht aus einem doppelten Prävalenzfehler und einem resultierenden Bezugsgrößentrugschluss (s. o.). Dem Prävalenzfehler liegt dabei die Verwechslung zweier Wahrscheinlichkeiten zu Grunde: Die Wahrscheinlichkeit, dass der Urheber einer DNA-Spur bei einem DNA-Vergleichstest positiv getestet wird, mit der Wahrscheinlichkeit, dass jemand, der in einer DNA-Rasterfahndung positiv getestet wird, der Urheber der Spur sein muss (für ein Rechenbeispiel[6] siehe Prävalenzfehler). Dabei wird die A-priori-Wahrscheinlichkeit falsch positiver Testergebnisse ebenso ignoriert wie die natürliche Prävalenz eines bestimmten genetischen Fingerabdrucks in einer hinreichend großen Grundgesamtheit.
Eine DNA-Rasterfahndung allein ist aber ungeeignet, eine ansonsten unverdächtige Person zu belasten. Liegt bereits eine Verdächtigung aufgrund anderer, von der Spur unabhängiger Umstände vor, so kann der Test den Verdacht erhärten oder zerstreuen. Seine Aussagekraft steigert sich, je kleiner die Grundgesamtheit der in Frage kommenden Urheber wird – im Beispiel ist diese sehr groß –, aber nur so lange, wie sichergestellt werden kann, dass der Urheber der Spur aus der Grundgesamtheit stammt. Damit von einer Übereinstimmung auf eine Urheberschaft geschlossen werden kann („3“ in der Abb. „Fehlschlüsse im DNA-Beweis“), muss zuerst ein Kreis von Menschen gefunden werden, der objektiv in Frage kommt – vor Gericht kann eine subjektiv vermutete A-priori-Wahrscheinlichkeit nicht akzeptiert werden. Dieses prinzipielle Problem taucht sowohl bei einer gerichtlichen Untersuchung („Täterkreis“) als auch bei einem Vaterschaftstest auf. Wenn man dort liest „Die Wahrscheinlichkeit, dass das Blut (am Tatort) von einer anderen Person als dem Verdächtigen stammt, ist 1 zu eine Million“, ist das also ein Fehlschluss.
Im Urhebertrugschluss wird die Kette der Bedingungen übersprungen und geschlossen, dass der Urheber einer DNA-Spur auch der Schuldige sein muss. Die scheinbare Folgerung „Da beide Proben mit einer Wahrscheinlichkeit von eins zu einer Million zufällig übereinstimmen, ist auch die Wahrscheinlichkeit der Unschuld eins zu einer Million, oder die Wahrscheinlichkeit der Schuld eine Million zu eins“, verbindet den Trugschluss des Anklägers mit einem Urhebertrugschluss. Nicht nur wird die Urheberwahrscheinlichkeit fälschlich viel zu hoch („Urhebertrugschluss“) angegeben, die Spur könnte auch „gelegt“ worden sein (4 in der Abb.) oder in einem anderen als dem Tatzusammenhang entstanden sein (5 in der Abb.).
Liste individueller Fehlschlüsse (Auswahl)
| Name | Erläuterung | Beispiel | Anmerkungen |
|---|---|---|---|
| A dicto simpliciter ad dictum secundum quid | Die fehlerhafte Anwendung einer allgemeinen Regel auf unstrittige Ausnahmen. | „Ich glaube daran, dass man niemals jemanden verletzen darf. Darum könnte ich nicht Chirurg sein.“ | Informeller Fehlschluss |
| A nescire ad non esse | Vom Fehlen von Information über einen Sachverhalt wird auf sein Nichtbestehen geschlossen | ||
| Affirming a Disjunct | Konstruktion eines disjunktiven Syllogismus hinsichtlich zweier Mengen, die gar nicht disjunkt sind | „Um eine Freundin wie die von Tom zu haben, musst du entweder reich oder berühmt sein. Tom ist reich, also kann er nicht berühmt sein.“ | |
| Appeal to Probability | Fälschliche Annahme, dass ein wahrscheinliches oder mögliches Ereignis auf jeden Fall tatsächlich eintreten wird | „Im Universum gibt es Milliarden von Galaxien mit Milliarden von Sternen. Also muss es einen anderen Planeten mit intelligentem Leben geben.“ | Spezialfall von Non sequitur |
| Affirming the Consequent (dt. Bejahung des Nachsatzes) | Unzulässige Umkehrung von Antezedens und Konsequenz | „Wenn die Lampe kaputt ist, ist es dunkel. Es ist dunkel. Also ist die Lampe kaputt.“ | Formallogischer Fehler |
| Confusion of the Inverse | Verwechslung einer bedingten Wahrscheinlichkeit mit ihrer Umkehrung | „Die meisten Unfälle passieren zu Hause. Um sicher zu sein, sollte man sich möglichst wenig zu Hause aufhalten.“ | Fehlbeurteilung der Wahrscheinlichkeit |
| Conjunction Fallacy | Fälschliche Annahme, dass ein speziellerer Fall mit größerer Wahrscheinlichkeit vorliegt als ein allgemeinerer Fall | „Linda hat Philosophie studiert und nimmt großen Anteil an gesellschaftlichen Themen wie Diskriminierung und sozialer Gerechtigkeit. Was ist wahrscheinlicher? 1. Linda ist Bankbeamtin. 2. Linda ist Bankbeamtin und in der Frauenbewegung aktiv.“ – „Antwort 2 natürlich.“ | Formaler Fehlschluss |
| Genetischer Fehlschluss | Eine These wird akzeptiert, weil die Entstehungs - und Ursprungsbedingungen angegeben werden. | Das Kind ist sehr unzuverlässig. Es wuchs bei den Müllers auf. | genetic fallacy |
| Ignoratio elenchi | Eine andere Behauptung bewiesen als die zur Debatte stehende; das Argument verfehlt das Thema. | "Bären können nicht gefährlich sein. Sie sind so niedlich." | „Fallacy of Irrelevant Conclusion“. Spezialfall: Red Herring. |
| Illicit Major | Schlussfolgerung, in der der Oberbegriff eine Distribution aufweist, die er in der ersten Prämisse nicht hat | „Alle Hunde sind Tiere. Katzen sind keine Hunde. Also sind Katzen keine Tiere.“ | Spezialfall von Non sequitur |
| Intentionaler Fehlschluss | |||
| Moralistischer Fehlschluss | |||
| Non sequitur | Sammelbegriff für Schlussfolgerungen, die aus den Prämissen gar nicht abgeleitet werden können. | „Das Universum hatte einen Anfang. Also hat es auch ein Ende.“ | Formaler Fehlschluss |
| Ökologischer Fehlschluss | |||
| Petitio principii | Spezialfall eines Zirkelschlusses | ||
| Quaternio Terminorum | Fehlschluss, der sich ereignet, wenn in einem Syllogismus nicht drei, sondern vier Begriffe verwendet werden. | „Alle Bäume sind Pflanzen. Alle Vögel sind Tiere. Darum sind alle Bäume Tiere.“ | Formaler Fehlschluss; siehe auch oben |
| Spielerfehlschluss | Die falsche Annahme, dass ein zufälliges Ereignis, wenn es längere Zeit nicht eingetreten ist, mit größerer Wahrscheinlichkeit eintreten wird, als wenn es erst kürzlich eingetreten ist. | „Ich habe jetzt schon zwanzig Würfe lang keine Sechs mehr gewürfelt. Einer der nächsten Würfe muss eine Sechs sein.“ | Verwechslung von Wahrscheinlichkeit und relativer Häufigkeit |
| Zirkelschluss | Das zu Beweisende wird als Beweis herangezogen | „M. ist ein großartiger Vermittler, weil er ein Händchen dafür hat, Streitende zusammenzubringen.“ | Formaler Fehlschluss (In diesem Falle als idem per idem) |
Siehe auch
- Eristische Dialektik, ein Versuch zur Klassifizierung von Fehl- und Trugschlüssen durch Arthur Schopenhauer
- Paralogismus (Kant) für die Paralogismen der reinen Vernunft bei Immanuel Kant
- Aequat causa effectum
- Beurteilung eines Klassifikators
- error in forma
- Fallacia fictae necessitatis
- Humes Gesetz
- Trugschluss der Komposition
- Filterblase & Echokammer-Effekt
- Informaler Fehlschluss
Literatur
- Rudolf Eisler: Wörterbuch der philosophischen Begriffe, 2. Auflage, Berlin 1904
- Gerrit Haas: Fehlschluß. In: Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. Band 2, 2., neubearbeitete Auflage, Metzler, Stuttgart/Weimar 2005, ISBN 3-476-02101-7, S. 479 f.
- Charles Leonard Hamblin: Fallacies, London: Methuen 1970, ISBN 0-416-14570-1 (gebundene Ausgabe), ISBN 0-416-70070-5 (Taschenbuchausgabe) – Standardwerk
- Frank Kannetzky: Paralogismus. In: Hans Jörg Sandkühler (Hrsg.): Enzyklopädie Philosophie. Band 2, Meiner, Hamburg 2010, ISBN 978-3-7873-1999-2, S. 1908–1912.
- Klaus Konhardt: Paralogismus. In: Historisches Wörterbuch der Philosophie. Band 7, Schwabe, Basel 1989, Sp. 107–115.
Weblinks
- Leo Groarke: Informal Logic. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- Hans Hansen: Fallacies. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- Bradley Dowden: Fallacies. In: J. Fieser, B. Dowden (Hrsg.): Internet Encyclopedia of Philosophy.
- Timm Grams: Denkfallen und Paradoxa. 2012, abgerufen am 19. Juni 2014.
- Gary N. Curtis: Taxonomy of the Logical Fallacies. In: Fallacy Files. Abgerufen am 19. Juni 2014 (englisch, Taxonomie der logischen Fehlschlüsse).
- Jesse Richardson, Andy Smith, Som Meaden: thou shalt not commit logical fallacies. 2014, abgerufen am 19. Juni 2014 (englisch, Übersicht über die häufigsten Fehlschlüsse im religiös/spirituellen Kontext).
- Don Lindsay: A List Of Fallacious Arguments. In: The Don Lindsay Archive. Abgerufen am 19. Juni 2014 (englisch, Liste von Fehlschlüssen).
- Logical fallacies. Abgerufen am 13. Juli 2020 (englisch, Liste von Fehlschlüssen).
Einzelnachweise
- Arthur Schopenhauer: Eristische Dialektik oder die Kunst, Recht zu behalten, unvollendetes Manuskript von 1830/31, gedruckt in: Schopenhauer, Arthur: Der handschriftliche Nachlaß. Band 3., München 1985.
- John Stuart Mill: A System of Logic, Ratiocinative and Inductive, Being a Connected View of the Principles of Evidence, and the Methods of Scientific Investigation, 1843 ((5. Buch)) – deutsch: System der deduktiven und induktiven Logik, übersetzt von J. Schiel, Braunschweig 1868.
- Charles Sanders Peirce: Collected Papers Band 2: Elements of Logic. hrsg. v. Charles Hartshorne/Paul Weiss, Cambridge, Mass., Harvard University Press, 2. Aufl., The Belknap Press, Cambridge, Mass. 1960. (CP), S. 2.622 ff.
- Gerd Gigerenzer: Das Einmaleins der Skepsis. Über den richtigen Umgang mit Zahlen und Risiken, Berlin 2002, ISBN 3-8270-0079-3.
- Gerd Gigerenzer: Das Einmaleins der Skepsis. Über den richtigen Umgang mit Zahlen und Risiken, Berlin 2002, ISBN 3-8270-0079-3.
- Nach Lindsey, Samuel; Hertwig, Ralph; Gigerenzer, Gerd: Communicating Statistical DNA Evidence. In: 43 Jurimetrics, 2003, S. 147 ff., 2003 Artikel auf heinonline.org. Abgerufen am 23. November 2010.