Relative Häufigkeit

Die relative Häufigkeit ist eine Gliederungszahl und ein Maß der deskriptiven Statistik. Sie gibt den Anteil der Elemente einer Menge wieder, bei denen eine bestimmte Merkmalsausprägung vorliegt. Sie wird berechnet, indem die absolute Häufigkeit eines Merkmals in einer zugrundeliegenden Menge durch die Anzahl der Objekte in dieser Menge geteilt wird. Die relative Häufigkeit ist also eine Bruchzahl und hat einen Wert zwischen 0 und 1.

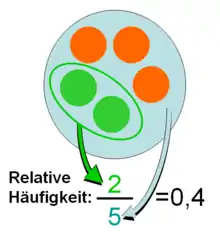
Berechnung der relativen Häufigkeit als Mengendiagramm

Allgemeine mathematische Definition

Relative Häufigkeiten werden bezüglich einer zugrundeliegenden Menge berechnet. Diese Menge kann sowohl eine Grundgesamtheit als auch eine Stichprobe sein. Um die relative Häufigkeit zu definieren, nehmen wir an, dass die zugrundeliegende Menge $n$ Elemente aufweist. Unter diesen $n$ Elementen tritt $H_{n}(A)$ -mal das Ereignis $A$ auf. Die relative Häufigkeit wird berechnet als die Anzahl der Beobachtungen mit dem Merkmal $A$ dividiert durch die Gesamtzahl aller Elemente in der zugrundeliegenden Menge.

Die relative Häufigkeit ergibt sich daher als

h_{n}(A)={\frac {H_{n}(A)}{n}}

.

$H_{n}(A)$ wird auch als absolute Häufigkeit bezeichnet. Im Gegensatz zur relativen Häufigkeit $h_{n}(A)$ sind sinnvolle Vergleiche zwischen Stichproben (oder Grundgesamtheiten) unterschiedlicher Größe mit der absoluten Häufigkeit $H_{n}(A)$ in der Regel nicht möglich.

Beispiele

Anteil der Mädchen in einer Schulklasse

In einer Klasse A sind 24 Schüler, davon 12 Mädchen. In Klasse B sind 18 Schüler, davon 9 Mädchen. Das heißt, in Klasse A sind mehr Mädchen (12) als in Klasse B (9), wenn man die absolute Häufigkeit betrachtet. Betrachtet man die Häufigkeit an Mädchen hingegen relativ zur jeweiligen Klassengröße, sieht man, dass in beiden Klassen der gleiche Anteil an Mädchen ist: In Klasse A ist die relative Häufigkeit an Mädchen 0,5 (= ¹²⁄₂₄) und in Klasse B ebenfalls 0,5 (= ⁹⁄₁₈). Die relative Häufigkeit lässt sich auch leicht in eine Prozentzahl umrechnen, indem man sie mit 100 % multipliziert. Somit bestehen beide Klassen zu 50 % (= 0,5 × 100 %) aus Mädchen.

Wahlumfragen

Bei einer Wahlumfrage werden 600 Wahlberechtigte in Bayern befragt, sowie 200 Wahlberechtigte in Berlin. In Bayern geben 120 Befragte an, die Partei A zu wählen. In Berlin sagen 100 Befragte, dass sie die Partei A wählen würden. Die absolute Häufigkeit für Wähler der Partei A ist also in Bayern höher als in Berlin, nämlich 120 Befragte in Bayern gegenüber 100 Befragten in Berlin. Dies ist jedoch auf den Umstand zurückzuführen, dass in Bayern drei Mal so viele Personen befragt wurden wie in Berlin. Ein Vergleich der absoluten Häufigkeiten ist daher nicht sinnvoll.

Im Gegensatz dazu ermöglicht die relative Häufigkeit einen Vergleich bezüglich der Popularität der Partei A zwischen Bayern und Berlin. In Bayern beträgt die relative Häufigkeit 0,2 (= ¹²⁰⁄₆₀₀). Für Berlin berechnet man als relative Häufigkeit 0,5 (= ¹⁰⁰⁄₂₀₀). Partei A ist in Berlin also wesentlich beliebter als in Bayern.

Eigenschaften

Im Gegensatz zur absoluten Häufigkeit bewegt sich die relative Häufigkeit immer zwischen 0 und 1. Dadurch kann man verschiedene relative Häufigkeiten miteinander vergleichen, obwohl sie sich auf eine unterschiedliche Bezugsgröße beziehen. In der deskriptiven Statistik werden relative Häufigkeiten daher verwendet, um Häufigkeitsverteilungen unabhängig von der Zahl der Elemente in der Grundgesamtheit (also unabhängig vom Stichprobenumfang) vergleichen zu können.

Im Rahmen der Inferenzstatistik und Stochastik wird die relative Häufigkeit als Maximum-Likelihood-Schätzer für den Parameter Erfolgswahrscheinlichkeit einer Binomialverteilung verwendet.

Für die relative Häufigkeit gelten folgende Rechenregeln:

$0\leq h_{n}(A)\leq 1$ aufgrund der Normierung auf die Anzahl $n$ der Wiederholungen.
$h_{n}(\Omega )=1\,$ für das sichere Ereignis.
$h_{n}(A\cup B)=h_{n}(A)+h_{n}(B)-h_{n}(A\cap B)$ für die Summe von Ereignissen.
$h_{n}({\bar {A}})=1-h_{n}(A)$ für das komplementäre Ereignis.

Relative Häufigkeit und Wahrscheinlichkeit

Frequentistischer Wahrscheinlichkeitsbegriff

Der frequentistische Wahrscheinlichkeitsbegriff interpretiert die Wahrscheinlichkeit eines Ereignisses als die relative Häufigkeit, mit der es in einer großen Anzahl gleicher, wiederholter, voneinander unabhängiger Zufallsexperimente auftritt. Dies ist die sogenannte ‚Limes-Definition‘ nach von Mises. Voraussetzung für diesen Wahrscheinlichkeitsbegriff ist die beliebige Wiederholbarkeit des Experiments; die einzelnen Durchgänge müssen voneinander unabhängig sein.[1]

Beispiel: Man würfelt 100 Mal und erhält folgende Verteilung: die 1 fällt 10 Mal (das entspricht einer relativen Häufigkeit von 10 %), die 2 fällt 15 Mal (15 %), die 3 ebenfalls 15 Mal (15 %), die 4 in 20 %, die 5 in 30 % und die 6 in 10 % der Fälle. Nach 10.000 Durchgängen haben die relativen Häufigkeiten sich – falls ein fairer Würfel vorliegt – in der Nähe der Wahrscheinlichkeiten stabilisiert, sodass z. B. die relative Häufigkeit für das Würfeln einer 3 ungefähr bei 16,6 % liegt.

Die heute als Grundlage der Wahrscheinlichkeitstheorie verwendete axiomatische Wahrscheinlichkeitsdefinition kommt ohne den Rückgriff auf den Begriff der relativen Häufigkeit aus.[2] Auch bei Verwendung dieser Wahrscheinlichkeitsdefinition existiert jedoch (mittels des Gesetzes der großen Zahlen) eine enge Beziehung zwischen Wahrscheinlichkeit und relativer Häufigkeit.[3]

Gesetz der großen Zahlen

Als Gesetze der großen Zahlen werden bestimmte Konvergenzsätze für die fast sichere Konvergenz und die Konvergenz in Wahrscheinlichkeit von Zufallsvariable bezeichnet.[3] In ihrer einfachsten Form besagen diese Sätze, dass sich die relative Häufigkeit eines Zufallsergebnisses in der Regel der Wahrscheinlichkeit dieses Zufallsergebnisses annähert, wenn das zu Grunde liegende Zufallsexperiment immer wieder durchgeführt wird.[3] Die Gesetze der großen Zahlen können von Kolmogorovs axiomatischer Wahrscheinlichkeitsdefinition ausgehend bewiesen werden. Somit existiert ein enger Zusammenhang zwischen relativer Häufigkeit und Wahrscheinlichkeit auch dann, wenn man kein Vertreter der objektivistischen Wahrscheinlichkeitsauffassung ist.

Literatur

Bernhard Rüger: Induktive Statistik. Einführung für Wirtschafts- und Sozialwissenschaftler. R. Oldenbourg Verlag, München Wien 1988, ISBN 3-486-20535-8.

Einzelnachweise

Bernhard Rüger (1988), S. 8 ff.
Bernhard Rüger (1988), S. 11 ff.
Bernhard Rüger (1988), S. 79 ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[rueger0-1] Bernhard Rüger (1988), S. 8 ff.

[rueger2-2] Bernhard Rüger (1988), S. 11 ff.

[rueger1-3] Bernhard Rüger (1988), S. 79 ff.