Elektromagnetische Welle

Eine elektromagnetische Welle, auch elektromagnetische Strahlung, ist eine Welle aus gekoppelten elektrischen und magnetischen Feldern. Bisweilen wird auch kurz von Strahlung gesprochen, wobei hier Verwechslungsgefahr zu anderer Teilchenstrahlung besteht. Beispiele für elektromagnetische Wellen sind Radiowellen, Mikrowellen, Wärmestrahlung, Licht, Röntgenstrahlung und Gammastrahlung (Aufzählung nach aufsteigender Frequenz). Elektromagnetische Wellen im Vakuum sind Transversalwellen. Die Wechselwirkung elektromagnetischer Wellen mit Materie hängt von ihrer Frequenz ab, die über viele Größenordnungen variieren kann.

Anders als zum Beispiel Schallwellen benötigen elektromagnetische Wellen kein Medium, um sich auszubreiten.[1] Sie können sich daher auch über weiteste Entfernungen im Weltraum ausbreiten. Sie bewegen sich im Vakuum unabhängig von ihrer Frequenz mit Lichtgeschwindigkeit fort. Elektromagnetische Wellen können sich aber auch in Materie ausbreiten (etwa einem Gas oder einer Flüssigkeit), ihre Geschwindigkeit ist dabei allerdings verringert. Der Brechungsindex gibt das Verhältnis an, um das die Phasengeschwindigkeit von elektromagnetischen Wellen in Materie geringer als die Lichtgeschwindigkeit im Vakuum ist.

Als Transversalwellen zeigen elektromagnetische Wellen das Phänomen der Polarisation. Im freien Raum stehen die Vektoren des elektrischen und des magnetischen Feldes senkrecht aufeinander und auf der Ausbreitungsrichtung. Die Transversalität ist unter Umständen verletzt, wenn – wie bei Plasmaschwingungen (Plasmonen) – Träger chemischer Eigenschaften, z. B. metallische oder gebundene Elektronen, beteiligt sind. Entsprechend unterscheiden sich die Quellen, Ausbreitungseigenschaften und Wirkungen der Strahlung in den verschiedenen Bereichen des elektromagnetischen Spektrums.

Entstehung

Elektromagnetische Wellen können durch unterschiedliche Ursachen entstehen:

Spontane Emission, wenn sich die Energie eines Atoms verringert. Dabei sind Energieänderungen der Atomhülle meist um Größenordnungen geringer als Energieänderungen des Atomkerns. Wird das Atom während der Zeitdauer der Energieabstrahlung „in Ruhe gelassen“ (wie in verdünnten Gasen), entsteht ein scharfes Linienspektrum. Das ist bei hohem Druck, wie in Höchstdrucklampen und beim Xenonlicht oder bei Atomen in Festkörpern nicht der Fall. Dort können wegen Druckverbreiterung keine wohldefinierten Spektrallinien mehr gemessen werden.
Bremsstrahlung: Elektromagnetische Wellen entstehen auch, wenn Ladungsträger beschleunigt werden. Das geschieht beispielsweise im Plasma der Sonne oder in der Röntgenröhre.
Molekülschwingungen (periodische Bewegungen von benachbarten Atomen in einem Molekül)
Larmorpräzession eines Teilchens mit einem magnetischen Dipolmoment um die Richtung eines von außen angelegten Magnetfelds.
Eine Bewegung von elektrisch geladenen Teilchen mit hoher Geschwindigkeit durch ein Medium. Wenn die Geschwindigkeit der Teilchen größer ist als die Phasengeschwindigkeit elektromagnetischer Wellen in diesem Medium, entsteht Tscherenkow-Strahlung.
Ein zeitlich veränderlicher elektrischer Strom gibt elektromagnetische Wellen ab. In der Funktechnik nutzt man dies mit Sende-Antennen zur drahtlosen Übertragung von Signalen.
Bei der Paarvernichtung wird Materie in elektromagnetische Strahlung verwandelt. Die Energie der Strahlung ergibt sich dabei aus der Masse und der kinetischen Energie der Teilchen.

Eigenschaften

Vorhandene elektromagnetische Wellen feststellen und messen

Empfänger für elektromagnetische Strahlung nennt man Sensoren oder Detektoren, bei Lebewesen Photorezeptoren. Radiowellen können durch Antennen detektiert werden.

An einer elektromagnetischen Welle lässt sich die Wellengeschwindigkeit messen, einerseits die im Vakuum universale Konstante Lichtgeschwindigkeit $c$ , sowie davon abweichende Werte für die Phasengeschwindigkeit $c_{\mathrm {med} }$ in einem durchlässigen (durchsichtigen) Medium. Messbar ist ferner die Intensität, gleichbedeutend mit der Leistung, bzw. mit der pro Zeit-Einheit durch einen bestimmten Querschnitt transportierten Energie.

Um die Wellenlänge zu messen, gibt es unterschiedliche Methoden, je nachdem, ob es sich um kürzere oder längere Wellenlängen handelt. Wellenlänge $\lambda$ und Frequenz $\nu$ lassen sich durch

\nu ={\frac {c_{\mathrm {med} }}{\lambda }}

ineinander umrechnen.

Wellencharakter

Physikalisch betrachtet handelt es sich bei elektromagnetischen Wellen um sich ausbreitende Schwingungen des elektromagnetischen Feldes. Hierbei stehen elektrisches und magnetisches Feld bei linear polarisierten Wellen senkrecht aufeinander und haben ein festes Größenverhältnis, welches durch die Wellenimpedanz gegeben ist. Insbesondere verschwinden elektrisches und magnetisches Feld an denselben Orten zur selben Zeit, so dass die häufig gelesene Darstellung, dass sich elektrische und magnetische Energie zyklisch ineinander umwandeln, im Fernfeld nicht richtig ist. Sie stimmt allerdings zum Beispiel für das Nahfeld eines elektromagnetische Wellen erzeugenden elektrischen Dipols oder Schwingkreises.

Die Entstehung elektromagnetischer Wellen erklärt sich aus den maxwellschen Gleichungen: Die zeitliche Änderung des elektrischen Feldes ist stets mit einer räumlichen Änderung des magnetischen Feldes verknüpft. Ebenso ist wiederum die zeitliche Änderung des magnetischen Feldes mit einer räumlichen Änderung des elektrischen Feldes verknüpft. Für periodisch (insbesondere sinusförmig) wechselnde Felder ergeben diese Effekte zusammen eine fortschreitende Welle.

Beispiele für Experimente, in denen der Wellencharakter zum Tragen kommt:

Erscheinungen wie Kohärenz und Interferenz lassen sich nur mit dem Wellenmodell erklären, weil dafür die Phase der Welle gebraucht wird.
Antennen für die von Rundfunksendern emittierte Strahlung sind auf die Größe der Wellenlänge abgestimmt. Beispielsweise ist eine effiziente Dipolantenne halb so lang wie die Wellenlänge. Eine Beschreibung der Strahlung als sehr große Anzahl an Photonen bietet keinen Vorteil, da es kein Messgerät gibt, um derart energiearme Photonen einzeln nachzuweisen.

Teilchencharakter

Für bestimmte Eigenschaften elektromagnetischer Wellen (z. B. photoelektrischer Effekt) genügt das oben beschriebene Wellenmodell nicht, um alle beobachtbaren Phänomene zu beschreiben, vielmehr treten die Teilcheneigenschaften einzelner Photonen, der Quanten des elektromagnetischen Feldes, in den Vordergrund. Der Wellencharakter (etwa Interferenz) bleibt aber voll erhalten. Man spricht deshalb vom Dualismus von Teilchen und Welle.

Im Rahmen dieser Teilchenvorstellung des Lichtes wird jeder Frequenz $f$ die Energie eines einzelnen Photons $h\cdot f$ zugeordnet, wobei $h$ das plancksche Wirkungsquantum ist. Andererseits haben auch Teilchen, wie zum Beispiel über mehrere Atome hinweg bewegte Elektronen, Welleneigenschaften (siehe auch Elektrischer Strom). Beide Aspekte elektromagnetischer Wellen lassen sich im Rahmen der Quantenelektrodynamik erklären.

Beispiele für Wirkungen, in denen der Teilchencharakter zum Tragen kommt:

Beim Compton-Effekt trifft eine elektromagnetische Welle mit etwa 20 pm Wellenlänge auf ein Elektron, dessen Wirkungsquerschnitt um etwa drei Größenordnungen kleiner ist. Zur Erklärung des physikalischen Ablaufes der Wechselwirkung muss also der Teilchencharakter des Lichts herangezogen werden. Jeder Versuch, die beobachtete Änderung der Wellenlänge mit dem Wellenmodell zu erklären, scheitert.
Beim photoelektrischen Effekt ist die kinetische Energie nicht von der Amplitude der Strahlung abhängig, sondern wächst linear mit der Frequenz. Dies ist nur über den Teilchencharakter erklärbar.
Die Erzeugung von Laserlicht beruht auf den Eigenschaften einzelner Atome, die jeweils kleiner sind als die erzeugte Wellenlänge. Deshalb muss man für die Erklärung der Herstellung auf das Photonenmodell zurückgreifen.

Photonen mit genügender Energie (etwa von einigen Elektronvolt aufwärts) wirken auf Materie ionisierend und können chemische (photochemische) Wirkungen auslösen, wenn die Bindungsenergien überschritten werden (Fotochemie). Diese chemische Wirksamkeit wird auch als Aktinität bezeichnet.

Wellen im Medium

Die Phasengeschwindigkeit $c_{\text{med}}$ mit der sich eine monochromatische Welle in einem Medium bewegt, ist typischerweise geringer als im Vakuum. Sie hängt in linearer Näherung von der Permittivität $\varepsilon$ und der Permeabilität $\mu$ des Stoffes ab,

c_{\text{med}}={\frac {1}{\sqrt {\mu \varepsilon }}}\,,

und ist damit abhängig von der Frequenz der Welle (siehe Dispersion) und bei doppelbrechenden Medien auch von ihrer Polarisation und Ausbreitungsrichtung. Die Beeinflussung der optischen Eigenschaften eines Mediums durch statische Felder führt zur Elektrooptik bzw. Magnetooptik.

Eine direkte Krafteinwirkung (z. B. Richtungsänderung) auf eine sich ausbreitende elektromagnetische Welle kann nur durch das Ausbreitungsmedium erfolgen (siehe Brechung, Reflexion, Streuung und Absorption) bzw. vermittelt werden (siehe Nichtlineare Optik und Akustooptischer Modulator).

Spektrum

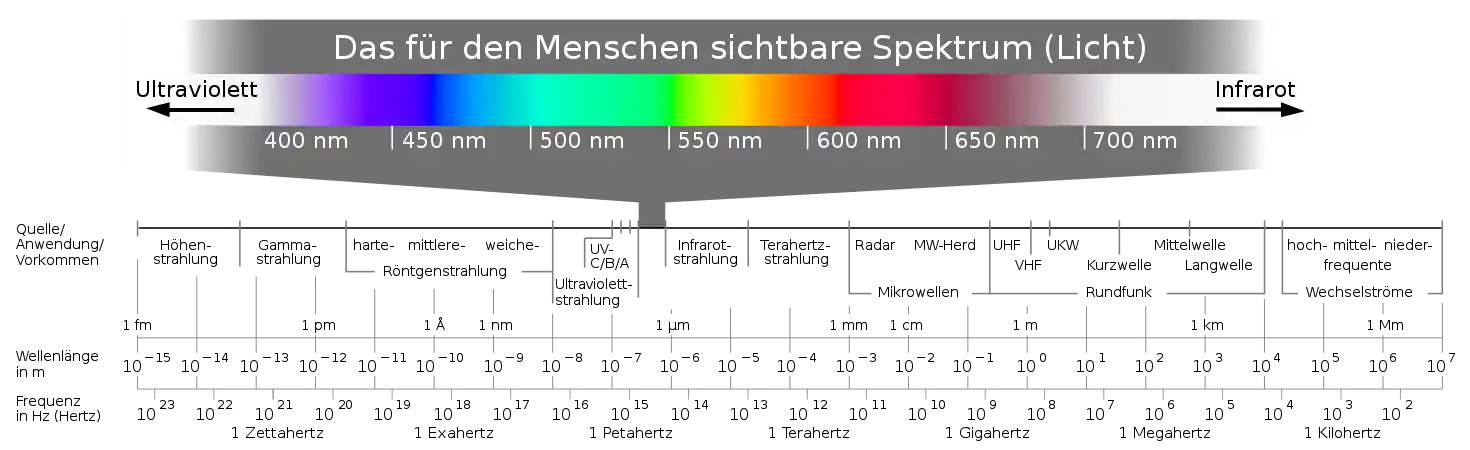
Elektromagnetische Wellen sind im elektromagnetischen Spektrum nach der Wellenlänge eingeteilt. Eine Liste von Frequenzen und Beispiele elektromagnetischer Wellen gibt es im entsprechenden Artikel.

Das sichtbare Licht stellt nur einen geringen Teil des gesamten Spektrums dar und ist, mit Ausnahme der Infrarotstrahlung (Wärme), der einzige Bereich, der von Menschen ohne technische Hilfsmittel wahrgenommen werden kann. Bei niedrigeren Frequenzen ist die Energie der Photonen zu gering, um chemische Prozesse auslösen zu können. Bei höheren Frequenzen hingegen beginnt der Bereich der ionisierenden Strahlung (Radioaktivität), bei der ein einziges Photon Moleküle zerstören kann. Dieser Effekt tritt bereits bei Ultraviolett-Strahlung auf und ist für die Bildung von Hautkrebs bei übermäßiger Sonnenexposition verantwortlich.

Beim Licht bestimmt die Frequenz die Farbe des Lichtes und nicht, wie oft fälschlicherweise angenommen, die Wellenlänge in einem Medium bei der Ausbreitung. Die Frequenz wird anders als die Wellenlänge beim Übergang in optisch dichtere Medien nicht beeinflusst. Da sich die Farbe aber beim Durchgang durch ein Medium nicht ändert, ist nur die Frequenz charakteristisch für die Farbe des Lichts. In Spektren wird aus historischen Gründen jedoch die Wellenlänge als charakteristische Eigenschaft angegeben. Der Zusammenhang zwischen Farbe und Wellenlänge gilt nur im Vakuum und in guter Näherung in Luft. Monochromatisches Licht, also Licht mit nur einer einzigen Wellenlänge, hat stets eine Spektralfarbe.

Übersicht über das elektromagnetische Spektrum, sichtbarer Anteil detailliert

Biologische und chemische Wirkung

Empfindlichkeitsverteilung der drei Zapfenarten beim Menschen: Schwarz gezeichnet ist die Empfindlichkeit der Stäbchen. Die Kurven sind jeweils so skaliert, dass ihr Maximum bei 100 % liegt.

Bei der Wechselwirkung von elektromagnetischer Strahlung mit biologischer Materie muss zwischen ionisierender Strahlung (größer 5 eV) und nicht-ionisierender Strahlung unterschieden werden. Bei der ionisierenden Strahlung reicht die Energie aus, um Atome oder Moleküle zu ionisieren, d. h. Elektronen herauszuschlagen. Dadurch werden freie Radikale erzeugt, die biologisch schädliche Reaktionen hervorrufen. Erreicht oder übersteigt die Energie von Photonen die Bindungsenergie eines Moleküls, kann jedes Photon ein Molekül zerstören, sodass beispielsweise eine beschleunigte Alterung der Haut oder Hautkrebs auftreten kann. Chemische Bindungsenergien stabiler Moleküle liegen oberhalb von etwa 3 eV pro Bindung. Soll es zu Moleküländerungen kommen, müssen Photonen mindestens diese Energie besitzen, was violettem Licht oder höherfrequenter Strahlung entspricht.

Bei der Wechselwirkung von nicht-ionisierender Strahlung unterscheidet man zwischen thermischen Effekten[2] (Strahlung wirkt erwärmend, weil sie durch das Gewebe absorbiert wird), direkten Feldeffekten (induzierte Dipolmomente, Änderung von Membran-Potentialen), Quanten-Effekten[3] und Resonanzeffekten (Synchronisation mit Schwingung der Zellstruktur).[4]

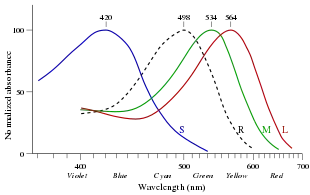
Ein Photon mit einer Wellenlänge von 700 nm oder kürzer kann im Molekül Rhodopsin die Änderung der Konformation hervorrufen. Im Auge wird diese Änderung aufgenommen und als Signal vom Nervensystem weiter verarbeitet. Die Empfindlichkeit für eine bestimmte Wellenlänge ändert sich bei Modifikationen des Rhodopsins. Dies ist die biochemische Grundlage des Farbsinns. Photonen von Licht mit einer Wellenlänge über 0,7 µm haben eine Energie unter 1,7 eV. Diese Wellen können keine chemischen Reaktionen an Molekülen bewirken, die bei Zimmertemperatur stabil sind. Aus diesem Grund können Tieraugen normalerweise keine Infrarot- oder Wärmestrahlung sehen. 2013 entdeckten Forscher jedoch, dass der Buntbarsch Pelvicachromis taeniatus im Nah-Infrarotbereich sehen kann.[5] Es gibt außerdem andere Sinnesorgane für Infrarotstrahlung, wie das Grubenorgan bei Schlangen.

Photonen können Schwingungen von Molekülen oder im Kristallgitter eines Festkörpers anregen. Diese Schwingungen machen sich im Material als thermische Energie bemerkbar. Zusätzliche durch elektromagnetische Wellen angeregte Schwingungen erhöhen die Temperatur des Materials. Anders als bei der Wirkung von einzelnen Photonen auf chemischen Bindungen, kommt es hierbei nicht auf die Energie der einzelnen Photonen an, sondern auf die Summe der Energie aller Photonen, also auf die Intensität der Strahlung. Durch Hitzedenaturierung kann langwellige elektromagnetische Strahlung auf indirekte Weise biologische Stoffe ändern.

Lichtgeschwindigkeit und spezielle Relativitätstheorie

Wie schnell sich Licht ungefähr ausbreitet, war seit 1676 bekannt. Allerdings fehlte bis 1865 jeder Zusammenhang zu anderen physikalischen Erscheinungen. Diesen konnte James Clerk Maxwell in den Jahren 1861 bis 1862 durch die von ihm gefundenen Maxwell-Gleichungen herstellen[6], welche die Existenz elektromagnetischer Wellen vorhersagen. Deren Geschwindigkeit stimmte mit der damals bekannten Lichtgeschwindigkeit so gut überein, dass sofort ein Zusammenhang hergestellt wurde. Diese Wellen konnte Heinrich Hertz in den 1880er-Jahren experimentell nachweisen.

In der klassischen Mechanik werden Wellen (in Ausbreitungsrichtung $x$ ) durch die Wellengleichung

{\frac {\partial ^{2}}{\partial t^{2}}}{\vec {f}}=c^{2}{\frac {\partial ^{2}}{\partial x^{2}}}{\vec {f}}

beschrieben. Hierbei bezeichnet ${\vec {f}}$ die Auslenkung der Welle und $c$ ihre Phasengeschwindigkeit, die hier als Ausbreitungsgeschwindigkeit der Welle interpretiert werden kann.

Aus den Maxwellgleichungen lässt sich im Vakuum für die elektrische Feldstärke ${\vec {E}}$ die Beziehung:

{\frac {\partial ^{2}}{\partial t^{2}}}{\vec {E}}={\frac {1}{\varepsilon _{0}\mu _{0}}}{\frac {\partial ^{2}}{\partial x^{2}}}{\vec {E}}

herleiten (in SI-Einheiten; siehe Abschnitt Mathematische Beschreibung). Die elektrische Feldstärke verhält sich in dieser Beziehung also wie eine Welle; die Größe

c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}

tritt als Ausbreitungsgeschwindigkeit auf. Diese Geschwindigkeit $c$ ist ausschließlich aus Naturkonstanten zusammengesetzt, die unabhängig vom Bezugssystem des Betrachters sind, was sich folglich auf die Größe $c$ überträgt.

Situation am Teich: Der bewegte Beobachter sieht die Ausbreitungsgeschwindigkeit einer Wasserwelle um seine eigene Geschwindigkeit verringert. Maxwell sagt für elektromagnetische Wellen voraus, dass die Ausbreitungsgeschwindigkeit c für beide Beobachter gleich ist.

Grundlage der klassischen Mechanik ist das galileische Relativitätsprinzip, das besagt, dass die Naturgesetze in allen Inertialsystemen – solchen Bezugssystemen, in denen Körper, auf die keine Kraft wirkt, sich geradlinig fortbewegen – dieselbe Form haben (Galilei-Invarianz). Ein sich zu einem Inertialsystem mit konstanter Geschwindigkeit fortbewegendes Bezugssystem ist ebenfalls ein Inertialsystem.

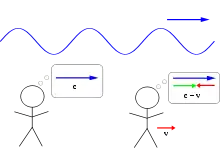
Nach diesem Relativitätsprinzip wäre nun zu erwarten, dass ein Beobachter, der sich mit einer konstanten Geschwindigkeit relativ zur elektromagnetischen Welle bewegt, eine unterschiedliche Ausbreitungsgeschwindigkeit misst, wie etwa ein mit konstanter Geschwindigkeit laufender Spaziergänger am Rande eines Teiches eine andere Ausbreitungsgeschwindigkeit einer Wasserwelle auf dem Teich feststellen würde als ein ruhender Beobachter. Die Maxwellgleichungen sagen aber für beide Beobachter die gleiche Ausbreitungsgeschwindigkeit voraus – sie sind nicht Galilei-invariant.

Dieser Widerspruch zur klassischen Mechanik löst sich zu Gunsten der Maxwellgleichungen auf: Die Tatsache, dass sich elektromagnetische Wellen in allen Inertialsystemen mit der gleichen Geschwindigkeit ausbreiten – die vielzitierte Konstanz der Lichtgeschwindigkeit – bildet ein Postulat in Einsteins 1905 veröffentlichter spezieller Relativitätstheorie. An Stelle der Galilei-Invarianz tritt die sogenannte Lorentz-Invarianz.

Mathematische Beschreibung

Die elektromagnetische Wellengleichung ergibt sich direkt aus den Maxwellgleichungen sowie der Divergenzfreiheit elektromagnetischer Wellen und lautet im Vakuum

\left(\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right){\vec {E}}({\vec {r}},t)=0

.

Betrachtet man die Ausbreitung elektromagnetischer Wellen in polarisierbaren Medien, so muss zusätzlich die Polarisation ${\vec {P}}$ betrachtet werden:

\left(\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right){\vec {E}}({\vec {r}},t)={\frac {1}{\varepsilon _{0}c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}{\vec {P}}

Herleitung der elektromagnetischen Wellengleichung

Die zur Wellenausbreitung gehörigen mathematischen Beziehungen lassen sich auf Basis der maxwellschen Gleichungen nachvollziehen. Insbesondere lässt sich dieselbe Form der Wellengleichung herleiten, mit der sich andere Arten von Wellen, beispielsweise Schallwellen, ausbreiten.

Im Vakuum, also im ladungsfreien Raum unter Ausschluss von dielektrischen, dia- und paramagnetischen Effekten sind die Materialgleichungen der Elektrodynamik ${\vec {D}}=\varepsilon _{0}{\vec {E}}$ und ${\vec {B}}=\mu _{0}{\vec {H}}$ . Außerdem sind die Stromdichte ${\vec {\jmath }}$ und Ladungsdichte $\varrho$ null.

Ausgehend von der dritten maxwellschen Gleichung

$\nabla \times {\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}$		(1)

wendet man auf beide Seiten den Rotationsoperator an. Dadurch erhält man:

\nabla \times (\nabla \times {\vec {E}})=-\nabla \times \left({\frac {\partial {\vec {B}}}{\partial t}}\right)=-\mu _{0}{\frac {\partial }{\partial t}}\left(\nabla \times {\vec {H}}\right)

.

Setzt man darin die vierte maxwellsche Gleichung (mit ${\vec {\jmath }}=0$ ) ein,

\nabla \times {\vec {H}}={\frac {\partial {\vec {D}}}{\partial t}}

,

ergibt sich

$\nabla \times (\nabla \times {\vec {E}})=-\mu _{0}{\frac {\partial }{\partial t}}\left({\frac {\partial {\vec {D}}}{\partial t}}\right)=-\mu _{0}\varepsilon _{0}{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}$ .		(2)

Dazu gilt ganz allgemein die vektoranalytische Beziehung

\nabla \times (\nabla \times {\vec {A}})=\nabla (\nabla \cdot {\vec {A}})-\Delta {\vec {A}}

.

Dabei ist mit $\Delta {\vec {A}}$ die Anwendung des vektoriellen Laplace-Operators auf das Vektorfeld ${\vec {A}}$ gemeint. In kartesischen Koordinaten wirkt der vektorielle Laplace-Operator wie der skalare Laplace-Operator $\textstyle \Delta ={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}$ auf jede Komponente von ${\vec {A}}$ .

Wendet man diese Beziehung auf ${\vec {E}}$ an und berücksichtigt, dass der ladungsfreie Raum betrachtet wird, in dem nach der ersten maxwellschen Gleichung die Divergenz von ${\vec {D}}$ null beträgt, so folgt:

$\nabla \times (\nabla \times {\vec {E}})=\nabla (\nabla \cdot {\vec {E}})-\Delta {\vec {E}}=-\Delta {\vec {E}}$ .		(3)

Setzt man nun (2) und (3) zusammen, ergibt sich folgende Wellengleichung:

$\Delta {\vec {E}}=\mu _{0}\varepsilon _{0}{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}$ .		(4)

Fast alle Wellen lassen sich durch Gleichungen der Form

{\frac {\partial ^{2}f}{\partial t^{2}}}=v^{2}\Delta f

beschreiben, wobei $v$ die Ausbreitungsgeschwindigkeit der Welle ist. Für die Ausbreitungsgeschwindigkeit elektromagnetischer Wellen, die Lichtgeschwindigkeit $c$ , gilt daher:

c^{2}={\frac {1}{\mu _{0}\varepsilon _{0}}}

.

Damit erhält man aus (4) die Gleichung

{\frac {\partial ^{2}{\vec {E}}}{\partial t^{2}}}=c^{2}\Delta {\vec {E}}

.

Analog kann man für die magnetische Flussdichte ${\vec {B}}$ die Beziehung

{\frac {\partial ^{2}{\vec {B}}}{\partial t^{2}}}=c^{2}\Delta {\vec {B}}

herleiten. Die Lösungen dieser Gleichungen beschreiben Wellen, die sich im Vakuum mit Lichtgeschwindigkeit $c$ ausbreiten. Breitet sich die elektromagnetische Welle in isotropem Material mit der Dielektrizitätskonstante $\varepsilon$ und der Permeabilität $\mu$ aus, beträgt die Ausbreitungsgeschwindigkeit

c_{\text{med}}={\frac {1}{\sqrt {\mu \varepsilon }}}

.

Darin sind aber im Allgemeinen die Materialkonstanten nicht linear, sondern können von der Feldstärke oder der Frequenz abhängen. Während Licht sich in der Luft fast mit Vakuumlichtgeschwindigkeit $c$ ausbreitet (die Materialkonstanten sind in guter Näherung 1), gilt das für die Ausbreitung in Wasser nicht, was unter anderem den Tscherenkow-Effekt ermöglicht.

Das Verhältnis der Vakuumlichtgeschwindigkeit zur Geschwindigkeit im Medium wird als Brechungsindex $n$ bezeichnet.

n={\sqrt {\frac {\mu \varepsilon }{\mu _{0}\varepsilon _{0}}}}={\sqrt {\mu _{r}\varepsilon _{r}}}

,

wo $\mu _{r}$ und $\varepsilon _{r}$ die relative Permeabilität und die relative Permittivität des Mediums bezeichnen.

Ausbreitung elektromagnetischer Wellen

Mit Hilfe der Maxwellgleichungen lassen sich aus der Wellengleichung noch weitere Schlüsse ziehen. Betrachten wir eine allgemeine ebene Welle für das elektrische Feld

{\vec {E}}={\vec {E}}_{0}f({\hat {k}}\cdot {\vec {x}}-ct)

,

wo ${\vec {E}}_{0}$ die (konstante) Amplitude ist, $f$ eine beliebige C²-Funktion, ${\hat {k}}$ ein Einheitsvektor, der in Propagationsrichtung zeigt, und ${\vec {x}}$ ein Ortsvektor. Zunächst sieht man durch Einsetzen in die Wellengleichung, dass $f({\hat {k}}\cdot {\vec {x}}-ct)$ die Wellengleichung erfüllt, dass also

\Delta f({\hat {k}}\cdot {\vec {x}}-ct)={\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}f({\hat {k}}\cdot {\vec {x}}-ct)

.

Damit ${\vec {E}}$ nun eine elektromagnetische Welle beschreibt, muss es aber nicht nur die Wellengleichung erfüllen, sondern auch die Maxwellgleichungen. Das bedeutet

\nabla \cdot {\vec {E}}={\hat {k}}\cdot {\vec {E}}_{0}{\frac {\partial f({\hat {k}}\cdot {\vec {x}}-ct)}{\partial ({\hat {k}}\cdot {\vec {x}})}}=0

,

{\vec {E}}\cdot {\hat {k}}=0

.

Das elektrische Feld steht also stets senkrecht zur Propagationsrichtung, es handelt sich also um eine Transversalwelle. Einsetzen von ${\vec {E}}$ in eine weitere Maxwellgleichung ergibt

\nabla \times {\vec {E}}={\hat {k}}\times {\vec {E}}_{0}{\frac {\partial f({\hat {k}}\cdot {\vec {x}}-ct)}{\partial ({\hat {k}}\cdot {\vec {x}})}}=-{\frac {\partial {\vec {B}}}{\partial t}}

und da $\textstyle -{\frac {\partial f({\hat {k}}\cdot {\vec {x}}-ct)}{\partial ({\hat {k}}\cdot {\vec {x}})}}={\frac {\partial f({\hat {k}}\cdot {\vec {x}}-ct)}{\partial (ct)}}$ ist, folgt daraus

{\vec {B}}={\frac {1}{c}}{\hat {k}}\times {\vec {E}}

.

Die magnetische Flussdichte in der elektromagnetischen Welle steht also ebenfalls senkrecht zur Propagationsrichtung und auch senkrecht zum elektrischen Feld. Außerdem stehen ihre Amplituden in einem festen Verhältnis. Ihr Quotient ist die Lichtgeschwindigkeit $c$

{\frac {E_{0}}{B_{0}}}\;=\;c

.

In natürlichen Einheiten ( $c=1$ ) haben beide Amplituden den gleichen Wert.

Mit dieser Beziehung lässt sich eine Aussage über die Energiedichte

w_{\mathrm {em} }={\frac {1}{2}}\varepsilon _{0}(E^{2}+c^{2}B^{2})

des elektromagnetischen Felds für den Fall der elektromagnetischen Welle herleiten:

w_{\mathrm {em} }=\varepsilon _{0}E^{2}={\frac {1}{\mu _{0}}}B^{2}

.

Nicht jede elektromagnetische Welle hat die Eigenschaft, dass ihre Ausbreitungsrichtung sowie die Richtungen des elektrischen als auch des magnetischen Feldes paarweise orthogonal zueinander sind, die Welle also eine reine Transversalwelle ist, auch TEM-Welle genannt. Die hier demonstrierten ebenen Wellen sind von diesem Typ, daneben existieren aber auch Wellen, in denen nur einer der beiden Feldvektoren senkrecht auf der Ausbreitungsrichtung steht, der andere aber eine Komponente in Ausbreitungsrichtung hat (TM- und TE-Wellen). Ein wichtiger Anwendungsfall für solche nicht rein transversale elektromagnetische Wellen sind zylindrische Wellenleiter. Das Gesagte gilt aber vor allem in Kristallen mit Doppelbrechung.[7] Allerdings gibt es keine rein longitudinalen elektromagnetischen Wellen.

Literatur

John David Jackson: Klassische Elektrodynamik. 4. Auflage. de Gruyter, Berlin u. a. 2006, ISBN 3-11-018970-4.
Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretische Elektrotechnik. Eine Einführung. 16. Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-20792-9.
Claus Müller: Grundprobleme der mathematischen Theorie elektromagnetischer Schwingungen (= Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen. 88, ISSN 0072-7830). Springer, Berlin u. a. 1957.
Eduard Rhein: Wunder der Wellen : Rundfunk u. Fernsehen, dargest. f. jedermann, Ausgabe 69.–80. Tsd., Deutscher Verl. d. Ullstein A.G., Berlin-Tempelhof 1954. DNB
Károly Simonyi: Theoretische Elektrotechnik. 10. Auflage. Barth, Leipzig u. a. 1993, ISBN 3-335-00375-6.

Weblinks

Commons: Elektromagnetische Welle – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Gerthsen Physik. 22., völlig neu bearbeitete Auflage. Springer, Berlin u. a. 2004, ISBN 3-540-02622-3, S. 177.
Kenneth R. Foster, Michael H. Repacholi: Biological Effects of Radiofrequency Fields: Does Modulation Matter? In: Radiation Research. Bd. 162, Nr. 2, 2004, S. 219–225, JSTOR 3581139.
Henrik Bohr, Søren Brunak, Jakob Bohr: Molecular wring resonances in chain molecules. In: Bioelectromagnetics. Bd. 18, Nr. 2, 1997, S. 187–189, doi:10.1002/(SICI)1521-186X(1997)18:2<187::AID-BEM13>3.0.CO;2-O.
Walter Hoppe, Wolfgang Lohmann, Hubert Markl, Hubert Ziegler (Hrsg.): Biophysik. 2., völlig neubearbeitete Auflage. Springer, Berlin u. a. 1982, ISBN 3-540-11335-5.
Reinhard Wandtner: Erster Nachweis bei Tieren: Infrarot beim Beutefang. In: Frankfurter Allgemeine Zeitung. 4. Februar 2013 (faz.net).
M. Guarnieri: Two Millennia of Light: The Long Path to Maxwell’s Waves. In: IEEE Industrial Electronics Magazine. 9, Nr. 2, 2015, S. 54–56+60. doi:10.1109/MIE.2015.2421754.
Näheres zur Kristalloptik (Doppelbrechung u. a.) in: W. Döring, Göschen-Bändchen zur Theoretischen Physik, Band „Optik“.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Gerthsen Physik. 22., völlig neu bearbeitete Auflage. Springer, Berlin u. a. 2004, ISBN 3-540-02622-3, S. 177.

[2] Kenneth R. Foster, Michael H. Repacholi: Biological Effects of Radiofrequency Fields: Does Modulation Matter? In: Radiation Research. Bd. 162, Nr. 2, 2004, S. 219–225, JSTOR 3581139.

[3] Henrik Bohr, Søren Brunak, Jakob Bohr: Molecular wring resonances in chain molecules. In: Bioelectromagnetics. Bd. 18, Nr. 2, 1997, S. 187–189, doi:10.1002/(SICI)1521-186X(1997)18:2<187::AID-BEM13>3.0.CO;2-O.

[4] Walter Hoppe, Wolfgang Lohmann, Hubert Markl, Hubert Ziegler (Hrsg.): Biophysik. 2., völlig neubearbeitete Auflage. Springer, Berlin u. a. 1982, ISBN 3-540-11335-5.

[5] Reinhard Wandtner: Erster Nachweis bei Tieren: Infrarot beim Beutefang. In: Frankfurter Allgemeine Zeitung. 4. Februar 2013 (faz.net).

[guarnieri_7-1-6] M. Guarnieri: Two Millennia of Light: The Long Path to Maxwell’s Waves. In: IEEE Industrial Electronics Magazine. 9, Nr. 2, 2015, S. 54–56+60. doi:10.1109/MIE.2015.2421754.

[7] Näheres zur Kristalloptik (Doppelbrechung u. a.) in: W. Döring, Göschen-Bändchen zur Theoretischen Physik, Band „Optik“.