Elastizität (Physik)
Elastizität ist die Eigenschaft eines Körpers oder Werkstoffes, unter Krafteinwirkung seine Form zu verändern und bei Wegfall der einwirkenden Kraft in die Ursprungsform zurückzukehren (Beispiel: Sprungfeder). Man unterscheidet dabei
- das linear-elastische Verhalten, das durch das Hookesche Gesetz beschrieben wird, es tritt generell bei kleinen Deformationen auf, sowie
- das nicht-linear-elastische Verhalten, bei dem die Spannung nichtlinear von der Deformation abhängt. Typisches Beispiel ist hier die Gummielastizität bei größeren Deformationen.
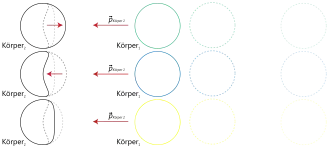
Bei allen Materialien gibt es eine Grenze des Elastizitätsbereichs, jenseits der ein plastisches Verhalten beobachtet wird. Dies ist der Fall, wenn nach Entfernen der auslenkenden Kräfte eine Deformation verbleibt.
Mechanismen
Wirkt auf einen Körper eine Kraft ein, so wird die Gleichgewichtslage seiner elementaren Bausteine (Atome oder Moleküle) gestört. Die Abstände zwischen ihnen werden um ein geringes Maß vergrößert oder verkleinert, die dazu aufgewendete mechanische Energie wird gespeichert und das Werkstück ändert seine äußere Form. Nach der Entlastung kehren die Atome bzw. Moleküle wieder an ihre Ausgangsplätze zurück und der Körper nimmt seine ursprüngliche äußere Form wieder an. Die Energie für die Verformung wird nur gespeichert und beim Entlasten wieder abgegeben.
Wird bei der Krafteinwirkung ein bestimmter Wert überschritten, so erfolgt zusätzlich zu der elastischen eine plastische Deformation. Dieser Wert ist jeweils materialabhängig und wird als Elastizitätsgrenze bezeichnet. Im Spannungs-Dehnungs-Diagramm ist es der Punkt, ab dem beim Entlasten eine Hysterese auftritt. Oft weicht hier die Spannungskurve auch vom linearen Verlauf ab. Dieser Punkt ist aber nicht eindeutig definiert, sondern von der Messmethode abhängig. Daher lässt sich u. a. eine zwingend eindeutige Zuordnung von Körpern und Materialien zu den Eigenschaften Elastizität und Plastizität häufig nicht durchführen, vielmehr gibt es nach Ausmaß, Art und Dauer der Krafteinwirkung eine Kombination aus beiden Eigenschaften oder einen Wechsel von elastischem zu plastischem Verhalten.
Eine besondere Form der Elastizität bildet die Viskoelastizität. Sie tritt vor allem bei Polymeren auf und ist durch ein teilweise elastisches, teilweise viskoses Verhalten geprägt. Das Polymer relaxiert nach Entfernen der externen Kraft nur unvollständig, die verbleibende Energie wird in Form von Fließvorgängen abgebaut. Hierbei bedeutet eine Erhöhung der Elastizität eine Verringerung des viskosen Verhaltens.
Modellierung
Die Elastizitätstheorie beschäftigt sich mit Materialmodellen mit denen die Eigenschaften von elastischen Körpern dargestellt werden können. Hierbei erlauben es Elastizitätsgesetze die im Material auftretenden Spannungen, aus den im Material erzwungenen Dehnungen zu berechnen. Es gibt Materialmodelle, die sowohl zur Hypo- als auch zur Cauchy-Elastizität gehören. Beide Theorien besitzen aber auch Mitglieder, die von der anderen Theorie nicht erfasst werden. Dissipative Vorgänge wie viskoses oder plastisches Fließen können meist nur bedingt oder gar nicht abgebildet werden.
Cauchy-Elastizität
In der Cauchy-Elastizität ist die Verformungsarbeit eines Körpers ausschließlich von der aktuellen Verformung bestimmt. Cauchy-Elastizität ist eine zeitunabhängige Materialeigenschaft. Die Elastizitätsgrenze kann in Feststoffen bei langsamen und hinreichend kleinen Verformungen eingehalten werden, wie sie in vielen technischen Anwendungen vorliegen.
Hyperelastizität
Die Hyperelastizität ist ein Spezialfall der Cauchy-Elastizität, der eintritt, wenn die Verformungsarbeit wegunabhängig ist. Durch das Modell der Hyperelastizität können nichtlineare elastische Verformungen dargestellt werden wie z. B. in Gummi oder organischem Gewebe.
Hypo-Elastizität
In Hypo-Elastischen Modellen ist die Änderung der Dehnungen eines Körpers eine ausschließlich von den Spannungen bestimmte lineare Funktion. Erst indem diese Funktion über die Zeit verfolgt wird, ergibt sich für das Materialgesetz die Spannungs-Dehnungs-Beziehung. Die Formulierung der Hypo-Elastizität ist derart allgemein, dass sie sogar Verbindungen zur Plastizitätstheorie aufweist.
Anwendungen
In der ingenieurwissenschaftlichen Festigkeitslehre, spezieller in der Baukonstruktion und der gerätetechnischen Konstruktion werden die elastischen Eigenschaften von Materialien dazu herangezogen, die Formstabilität von Bauwerken und Geräten unter Krafteinwirkung zu gewährleisten. In der Balkentheorie nimmt die Elastizität einen zentralen Bestandteil ein. Mit der Berechnung der Elastizität wird auch eine hohe Belastung tragender Konstruktionen bei gleichzeitiger Vermeidung von Bruchgefahren erreicht.
Um die Elastizität von Werkstoffen rechnerisch in linearer Näherung behandeln zu können, werden drei Moduli unterschieden, die über die Poissonzahl miteinander verknüpft sind:
- dem Elastizitätsmodul; es beschreibt den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers bei linear-elastischem Verhalten.
- dem Kompressionsmodul; mit seiner Hilfe wird berechnet, welche allseitige Druckänderung nötig ist, um eine bestimmte reversible Volumenänderung hervorzurufen.
- dem Schubmodul; es gibt Auskunft über die linear-elastische Verformung eines Bauteils infolge einer Scherkraft oder Schubspannung.
Das linear-elastische Verhalten einiger Materialien bei kleinen Verformungen wird für die Konstruktion und Anwendung von Federn ausgenutzt, siehe Federkonstante.
In der Rheologie ist die lineare Elastizität neben der Plastizität und der Viskosität eine der drei Grundeigenschaften und wird in den rheologischen Modellen durch eine Feder, das Hooke-Element, dargestellt.
Die Aeroelastizität und deren Simulation finden in der Luft- und Raumfahrt aber auch in Windkraftanlagen Anwendung.[1][2]
Siehe auch
- Ursache der Elastizität von Elastomeren zum Thema Energie- und Entropie-Elastizität
- Streuung (Physik) von Teilchen und/oder Quanten, die als elastisch oder unelastisch bezeichnet werden
- Stoß (Physik)
- Love-Zahlen
Literatur
- Wilhelm Westphal: Physik. Ein Lehrbuch für Studierende an den Universitäten und Technischen Hochschulen. 2. Auflage. Springer, Berlin 1930.
- Ernst Grimsehl: Grimsehl Lehrbuch der Physik. Band 1: Mechanik · Akustik · Wärmelehre. 27., unveränderte Auflage. Teubner, Leipzig 1991, ISBN 3-322-00812-6.
Weblinks
- Lexikon der Physik: Elastizität (abgerufen am 8. April 2016)
- Elastizität und Festigkeitslehre (abgerufen am 8. April 2016)
- Lehrbuch Festkörpermechanik (englisch)
Einzelnachweise
- Windenergieanlagen. DLR - Institut für Aeroelastik, abgerufen am 4. September 2021.
- Martin O. L. Hansen: Aerodynamics of Wind Turbines. Earthscan, 2008, abgerufen am 4. September 2021 (englisch).