Kernreaktion

Eine Kernreaktion ist ein physikalischer Prozess, bei dem ein Atomkern durch den Zusammenstoß mit einem anderen Atomkern oder Teilchen seinen Zustand oder seine Zusammensetzung ändert. Häufig werden die elastischen Stöße von Kernen nicht dazu gerechnet, weil sich dabei nur die Impulse der beiden Stoßpartner ändern, manchmal auch nicht die unelastischen Stöße, bei denen zusätzlich einer der Stoßpartner in einen angeregten Zustand versetzt wird. Bei den übrigen Fällen – den Kernreaktionen im eigentlichen Wortsinn – ändern die Kerne durch Abgeben oder Aufnehmen von Teilchen ihre Zusammensetzung. Die Gesamtzahl der vorhandenen Nukleonen bleibt aber stets erhalten, in den meisten betrachteten Fällen auch die Neutronen- und die Protonenzahl je für sich.

Nicht zu den Kernreaktionen zählt der radioaktive Zerfall, weil hier die Kernumwandlung spontan erfolgt, also nicht durch einen Stoß ausgelöst wird.

Mit der Erforschung von Kernreaktionen befassen sich vor allem die Kernphysik und die Teilchenphysik. Eine wichtige Rolle spielen Kernreaktionen bei der Entstehung der Nuklide, s. Astrophysik, Kosmochemie. Anwendungen gibt es z. B. in der Energietechnik (siehe Kernreaktor, Fusionsreaktor) und der Medizintechnik (Herstellung von Radionukliden für Nuklearmedizin und Strahlentherapie).

Aus Impulserhaltung und Energieerhaltung ergeben sich bei den Kernreaktionen bestimmte Beschränkungen. Sie werden im Artikel Kinematik beschrieben. Auch andere Erhaltungsgrößen wie die Baryonenzahl spielen eine Rolle.

Geschichte

Ernest Rutherford benutzte ab 1911 Alphateilchen aus einer radioaktiven Substanz in seinen Streuversuchen, bei denen er deren elastische Streuung an Gold-Atomkernen beobachtete. Die erste Beobachtung einer Kernreaktion im engeren Sinn, ebenfalls durch Rutherford, datiert von 1919: Alphateilchen wurden durch Stickstoff geschossen, was dahinter auf dem Zinksulfid-Schirm, der als Szintillator diente, auch Signale von Protonen ergab. Rutherford nahm dabei irrtümlich zuerst an, die Alphateilchen würden ein Proton aus dem Kern herausschlagen und so Kohlenstoff erzeugen.[1] Dass die Alphateilchen jedoch mit dem Kern verschmolzen, dabei ein Proton auslösten und so Sauerstoff erzeugten (Reaktion: ¹⁴N + α → ¹⁷O + p), wurde erst 1925 von Patrick Blackett nachgewiesen.[2]

Die weitere Erforschung und Nutzung von Kernreaktionen beruhte überwiegend auf künstlich beschleunigten Geschossteilchen und war daher eng verbunden mit der Entwicklung der Teilchenbeschleuniger. John Cockcroft und Ernest Walton gelang 1930 der erste Nachweis einer durch künstlich beschleunigte Teilchen ausgelösten Kernreaktion – damals stolz als Kernzertrümmerung bezeichnet. Sie bestrahlten Lithium mit Protonen der kinetischen Energie 300 keV; als Reaktionsprodukte wurden Helium-4-Atomkerne (Alphateilchen) beobachtet.[3] Es handelte sich also um die Reaktion ⁷Li + p → 2 ⁴He. Die von ihnen bestimmte Energie- und Massenbilanz wurde zum ersten experimentellen Nachweis der „Umwandlung von Masse in Energie“ nach Einsteins Gleichung E=mc².

Formelschreibweise und Beispiele

Beispiel einer Kernreaktion:

{}_{3}^{6}\mathrm {Li} +{}_{1}^{2}\mathrm {H} \rightarrow 2\ {}_{2}^{4}\mathrm {He}

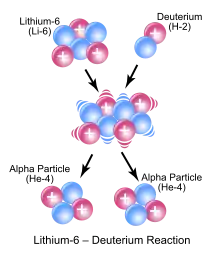
In dem als Beispiel gezeigten symbolischen Bild reagieren ein ⁶Li-Kern und ein Deuterium-Kern (ein Deuteron) und bilden den Zwischenkern ⁸Be, der unmittelbar darauf in zwei Alphateilchen zerfällt.

Eine Kernreaktion kann durch eine Formel ähnlich einer chemischen Gleichung dargestellt und überprüft werden. Kernzerfälle können ähnlich dargestellt werden, allerdings steht dann nur ein Kern auf der linken Seite. Jedes Teilchen, das an der Reaktion teilnimmt, wird mit seinem chemischen Symbol geschrieben, mit der Massenzahl links oben und der Ordnungszahl links unten. Da die Ordnungszahl durch das chemische Symbol eindeutig festgelegt ist, kann sie auch weggelassen werden.

Die Formel zum abgebildeten Beispiel lautet

{}_{3}^{6}\mathrm {Li} +{}_{1}^{2}\mathrm {H} \rightarrow {}_{2}^{4}\mathrm {He} +{}_{2}^{4}\mathrm {He}

oder vereinfacht

{}_{3}^{6}\mathrm {Li} +{}_{1}^{2}\mathrm {H} \rightarrow 2\ {}_{2}^{4}\mathrm {He}

.

Das Neutron wird als n geschrieben, das Proton kann als ¹H oder p geschrieben werden. Manche Teilchen kommen in so vielen betrachteten Reaktionen vor, dass man sie üblicherweise abkürzt. So wird beispielsweise der ⁴He-Kern mit dem griechischen Buchstaben α bezeichnet. Deuteronen (schwerer Wasserstoff, ²H) werden mit d bezeichnet.

Bei vielen interessierenden Reaktionen trifft ein relativ leichtes Teilchen (Nukleon oder leichter Kern, das Projektil) auf einen verhältnismäßig schweren Kern, ein Teilchen aus derselben „leichten“ Klasse (das Ejektil) wird emittiert, und ein anderer Kern bleibt zurück. In diesen Fällen kann die Reaktion vereinfacht folgendermaßen geschrieben werden

\mathrm {Ausgangskern} \;(\mathrm {Projektil} ,\mathrm {Ejektil} )\;\mathrm {Endkern}

.

Der Ausgangskern wird oft als Targetkern bezeichnet (von englisch target ‚Zielscheibe‘).
Projektil bzw. Ejektil sind meist Protonen, Deuteronen, Heliumkerne, Tritonen, Neutronen, Gammaquanten usw.

Mit Teilchensymbolen lautet die Formel dann beispielsweise

{}_{3}^{6}\mathrm {Li} +\mathrm {d} \rightarrow \alpha +\alpha

,

mit weggelassenen Ordnungszahlen

{}^{6}\mathrm {Li} +\mathrm {d} \rightarrow \alpha +\alpha

oder in komprimierter Form

{}^{6}\mathrm {Li} (\mathrm {d} ,\alpha )\alpha

.

Weitere Beispiele

Aus einem Atomkern von Silber-107 entsteht unter Einfang eines Neutrons und Aussendung eines γ-Quants Silber-108:

¹⁰⁷Ag(n,γ)¹⁰⁸Ag

¹⁴N wird durch ein Neutron der Höhenstrahlung in ¹⁴C verwandelt (durch diesen Prozess wird laufend ¹⁴C erzeugt, die Basis der Radiokohlenstoffdatierung):

¹⁴N(n,p)¹⁴C

Ein Lithium-6-Kern absorbiert ein Neutron und geht dadurch über in ein Triton und einen Helium-4-Kern:

⁶Li(n,t)⁴He

Die in den Beispielen angeführten Reaktionstypen (gleichgültig mit welchem Targetnuklid) bezeichnet man kurz als (d,α)-, (n,γ)-, (n,p)- bzw. (n,t)-Reaktionen.

Spezielle Arten von Kernreaktionen und Sonderfälle

Die komprimierte Schreibweise wird auch für Streuprozesse verwendet. Zum Beispiel steht ¹²C(n,n)¹²C oder kurz ¹²C(n,n) für die elastische Streuung eines Neutrons an einem Kohlenstoff-12-Kern. Eine unelastische Streuung wird durch einen Strich am ausfallenden Teilchen angedeutet, z. B. ¹²C(n,n') oder ¹²C(α,α').

Bei der insbesondere mit thermischen Neutronen wichtigen (n, $\gamma$ )-Reaktion spricht man von Neutroneneinfang oder Neutronenanlagerung, bei (p, $\gamma$ ) entsprechend von Protonenanlagerung.

Sonderfälle hinsichtlich der Schreibweise sind die induzierte Kernspaltung und die Spallation. Eine bestimmte Spaltungsreaktion, z. B. die erste bekannte, von Otto Hahn und Mitarbeitern entdeckte, lässt sich, je nach Anzahl der freigesetzten Neutronen, als ²³⁵U + n → ¹⁴⁰Ba + ⁹⁴Kr + 2n oder ²³⁵U + n → ¹⁴⁰Ba + ⁹³Kr + 3n schreiben (s. Entdeckung der Kernspaltung). Wenn jedoch – wie in der Praxis häufig – im Einzelfall nicht interessiert, welches der vielen möglichen Paare von Spaltprodukten entsteht und wie viele neue Neutronen emittiert werden, wird einfach ²³⁵U(n,f) geschrieben (f für engl. fission ‚Spaltung‘).

Bei der Spallationsreaktion wird, ausgelöst durch ein hochenergetisches Teilchen, ein Kern in viele Bruchstücke zerschlagen; hier ist die Schreibweise im genannten Formelstil offensichtlich wenig sinnvoll.

Reaktionsmechanismen

Kernreaktionen beruhen meist auf der starken und der elektromagnetischen Wechselwirkung, in bestimmten Fällen auch nur der letzteren allein. Die schwache Wechselwirkung spielt bei Kernreaktionen in der irdischen Umgebung praktisch keine Rolle, ist jedoch bei astrophysikalischen Vorgängen wichtig; in solchen Fällen kommt es auch zu Umwandlungen von Neutronen in Protonen oder umgekehrt.

Die experimentellen Beobachtungen legen nahe, dass Kernreaktionen je nach den beteiligten Kernen/Teilchen und je nach Stoßenergie auf sehr verschiedene Weise verlaufen können. Die nachstehend beschriebenen Typen, Zwischenkernreaktion und direkte Reaktion, sind nur idealisierte Grenzfälle; tatsächlich beobachtete Reaktionen sind meist Mischungen aus den Typen, d. h. die entstehenden Teilchen, Strahlungen usw. stammen anteilig aus den verschiedenen Prozessen.[4]

Zwischenkernreaktionen

Ist die Stoßenergie klein im Vergleich zur Bindungsenergie eines Protons oder Neutrons im Kern (diese beträgt im Durchschnitt über alle Nuklide etwa 9 MeV), lassen sich die Beobachtungen oft gut durch das Zwischenkernmodell erklären: Die beiden zusammenstoßenden Teilchen/Kerne verbinden sich zu einem neuen Kern, der dann unabhängig von der Art seiner Entstehung wieder in zwei oder mehr Teile zerfällt. Typische Kennzeichen einer Zwischenkernreaktion sind:

Resonanzen in der Anregungsfunktion
Vorwärts-Rückwärts-Symmetrie, d. h. Spiegelsymmetrie um die 90-Grad-Richtung der im Schwerpunktsystem betrachteten Winkelverteilung

Direkte Reaktionen

Bei höheren Stoßenergien treten dagegen direkte Reaktionsmechanismen in den Vordergrund. Dabei werden ein oder mehrere Nukleonen zwischen den Kernen ausgetauscht. Sie werden auch als Transferreaktionen bezeichnet.[5] Hierzu zählt z. B. die Strippingreaktion (engl. stripping ‚abstreifen‘), die besonders bei Deuteronen als Geschossen wichtig ist. Das relativ schwach gebundene Deuteron zerreißt dabei in seine beiden Bestandteile Neutron und Proton; dasjenige Teilchen, dass dem Targetkern nahe genug gekommen ist, wird absorbiert, während das andere weiterfliegt. Es ergibt sich also eine (d,n)- oder (d,p)- Reaktion. Auch die (d,np)-Reaktion ist als direkte Reaktion (engl. deuteron breakup ‚Aufbrechen des Deuterons‘) möglich, wenn das Deuteron im Kraftfeld des Targetkerns zerreißt, aber keine Absorption erfolgt. Strippingreaktionen spielen auch, wenngleich mit geringerer Wahrscheinlichkeit, z. B. als (³He,d)-, (⁶Li, d)-Reaktionen usw. eine Rolle.

Andere direkte Reaktionen sind die Pickup-Reaktion (engl. pick up ‚aufgreifen‘, ‚mitnehmen‘), bei der das Geschossteilchen ein Nukleon aus dem Targetkern absorbiert und mitnimmt, z. B. eine (p,d)- oder (d,³He)-Reaktion, und die Kickoff-Reaktion (engl. kick off ‚wegstoßen‘), z. B. vom Typ (n,p). (n,p)-Reaktionen tragen z. B. wesentlich zur Materialaktivierung durch schnelle Neutronen in Fusionsreaktoren bei.

Typisch für direkte Reaktionen sind

eine mit der Stoßenergie über einen größeren Bereich monoton ansteigende Anregungsfunktion
eine starke Bevorzugung kleiner Reaktionswinkel, also ein „Vorwärtspeak“ der Winkelverteilung.

Alle als direkte Reaktion möglichen Reaktionstypen sind, wie oben erwähnt, auch als Zwischenkernreaktion möglich. Oft sind Überlagerungen beider Grundtypen zu beobachten, z. B. eine Anregungsfunktion mit glattem, allmählich ansteigendem Untergrund und einzeln darauf sitzenden Resonanzen.

Q-Wert und Energiebilanz

Da die Bindungsenergie pro Nukleon in verschiedenen Kernen unterschiedlich ist, verlaufen manche Kernreaktionen exotherm, d. h. sie setzen Energie zusätzlich zur vorhandenen kinetischen Energie frei. Andere verlaufen endotherm, also unter Aufnahme von Energie; diese muss dann als kinetische Energie durch einen oder beide Reaktionspartner "mitgebracht" werden (Schwellenenergie), damit die Reaktion möglich ist (also ihr Wirkungsquerschnitt von Null verschieden ist). Energien werden in der Kernphysik meist in Megaelektronenvolt (MeV) angegeben.

Die überschüssige Energie exothermer Reaktionen kann als kinetische Energie der Reaktionsprodukte und/oder als Gammastrahlung freigesetzt werden.

Auch exotherme Reaktionen können eine Aktivierungsenergie benötigen. Dies gilt immer bei gleichnamig geladenen Reaktionspartnern, weil die elektrische Abstoßung überwunden werden muss; wegen des Tunneleffektes ist diese Aktivierungsenergie allerdings nicht scharf definiert. Wenn ein Stoßpartner ungeladen (Neutron oder Photon) ist, spielt die elektrische Abstoßung keine Rolle, aber auch dann kann eine Mindestenergie nötig sein, um etwa einen genügend hohen Anregungszustand des Zwischenkerns zu erreichen. Ein Beispiel hierfür ist die neutroneninduzierte Spaltung von Kernen mit gerader Neutronenzahl.

Bei der Schreibweise entsprechend einer chemischen Gleichung kann zusätzlich der Energiegewinn oder -verlust Q angegeben werden:

Anfangskern + Projektil → Endkern + Ejektil + Q.

Das letzte der oben genannten Beispiele, der Brutprozess im Blanket eines Fusionsreaktors, lautet so geschrieben:

\ {}_{3}^{6}\mathrm {Li} \ +\mathrm {n} \ \to \ {}_{2}^{4}\mathrm {He} \ +\ {}_{1}^{3}\mathrm {H} \ +\ 4{,}8\;\mathrm {MeV} \ \

Dieser Energiebetrag (in der Kernphysik üblicherweise nur „Q-Wert“ genannt) ist bei exothermer Reaktion positiv, bei endothermer negativ. Er gibt die Differenz zwischen der gesamten kinetischen Energie vor und nach der Reaktion an und lässt sich nach E = m c² aus der Differenz der Gesamtmassen auf der Anfangsseite und der Endseite ermitteln. Der Massenunterschied im oben angegebenen Beispiel ist

M\left(^{6}\mathrm {Li} \right)+M(\mathrm {n} )-M\left(^{4}\mathrm {He} \right)-\ M\left(^{3}\mathrm {H} \right)

=6{,}015122\ \mathrm {u} +1{,}008665\ \mathrm {u} -4{,}002603\ \mathrm {u} -3{,}016029\ \mathrm {u}

=0{,}005155\ \mathrm {u}

Die Atomare Masseneinheit u entspricht dem Energiebetrag

1\,\mathrm {u} \,c^{2}=931{,}49\ \mathrm {MeV}

,

daher ergibt sich der Q-Wert zu

Q=0{,}005155\ \mathrm {u} \cdot \left(931{,}49\ {\frac {\mathrm {MeV} }{\mathrm {u} }}\right)=4{,}802\ \mathrm {MeV}

, wie oben angegeben.

Man kann in den Kernmassen den Anteil $A\,\mathrm {u}$ ( $A$ ist die jeweilige Nukleonenanzahl) von vornherein weglassen, weil er sich in der Differenzbildung ohnehin heraushebt. Man verwendet also statt der Massen die Massenexzesse und vermeidet so die Ermittlung einer kleinen Differenz großer Zahlen. Dies ist bei nicht digitalen Berechnungen eine nützliche Erleichterung.

Statistische Schwankungen

Trifft ein gegebener, konstanter Strom von Projektilteilchen auf ein gegebenes Ziel, lässt sich aus dem Wirkungsquerschnitt der interessierenden Reaktion die Kernreaktionsrate (Anzahl der Reaktionen pro Zeitintervall) berechnen. Diese ist jedoch nur ein statistischer Mittelwert. Die tatsächlich in einer bestimmten Zeitdauer beobachtete Anzahl von Reaktionen schwankt zufällig um diesen Mittelwert; die Häufigkeit, mit der die einzelnen möglichen Anzahlen auftreten, folgt der Poisson-Verteilung. Somit ist Strahlung aus einer Kernreaktion (mit konstanter Reaktionsrate) auf die gleiche Art statistisch verteilt wie die aus einer radioaktiven Quelle.

Literatur

Herman Feshbach: Theoretical Nuclear Physics, Band 2: Nuclear Reactions, Wiley 1992

Weblinks

Wiktionary: Kernreaktion – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Tabelle der Atommassen
Script zur Berechnung von Energiebilanzen von Kernreaktionen
Q Value Calculator zur Q-Wert-Berechnung

Einzelnachweise

E. Rutherford: Collision of α particles with light atoms. IV. An anomalous effect in nitrogen. In: Philosophical Magazine. Band 37, 1919, S. 581–587. (Veröffentlichungstext)
Blackett, Patrick Maynard Stewart (2 Feb. 1925) "The Ejection of Protons From Nitrogen Nuclei, Photographed by the Wilson Method", Journal of the Chemical Society Transactions. Series A, 107(742), pp. 349–60
Eric B. Paul, Nuclear and Particle Physics, North-Holland Publ. Comp., 1969
Bethge, Walter, Wiedemann: Kernphysik. 2. Auflage, Springer Verlag 2001
Transferreaktionen, Lexikon der Physik, Spektrum Verlag

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] E. Rutherford: Collision of α particles with light atoms. IV. An anomalous effect in nitrogen. In: Philosophical Magazine. Band 37, 1919, S. 581–587. (Veröffentlichungstext)

[2] Blackett, Patrick Maynard Stewart (2 Feb. 1925) "The Ejection of Protons From Nitrogen Nuclei, Photographed by the Wilson Method", Journal of the Chemical Society Transactions. Series A, 107(742), pp. 349–60

[3] Eric B. Paul, Nuclear and Particle Physics, North-Holland Publ. Comp., 1969

[4] Bethge, Walter, Wiedemann: Kernphysik. 2. Auflage, Springer Verlag 2001

[5] Transferreaktionen, Lexikon der Physik, Spektrum Verlag