Elektrische Spannung

Die elektrische Spannung (oft auch vereinfacht nur als Spannung bezeichnet) ist eine grundlegende physikalische Größe der Elektrotechnik und Elektrodynamik. Ihr Formelzeichen ist das $U$ .[1] Sie wird im internationalen Einheitensystem in der Einheit Volt (Einheitenzeichen: V) angegeben. Zur Kennzeichnung einer Zeitabhängigkeit verwendet man den Kleinbuchstaben $u$ für den Augenblickswert der Spannung.[2][3] Im Angelsächsischen wird das Formelzeichen $V$ verwendet.[Anmerkung 1]

Physikalische Größe

Name

Elektrische Spannung

Formelzeichen

$U$

Größen- und Einheitensystem	Einheit	Dimension
SI	V	M·L²·I⁻¹·T⁻³
Gauß (cgs)	statV	M^½·L^½·T⁻¹
esE (cgs)	statV	M^½·L^½·T⁻¹
emE (cgs)	abV = erg·s⁻¹·Bi⁻¹	L^3/2·M^½·T

Vereinfacht gesagt – und in alltäglichen Stromkreisen passend – charakterisiert die Spannung die „Stärke“ einer Spannungsquelle; sie ist die Ursache für den elektrischen Strom, der die elektrische Ladung transportiert. Wenn beispielsweise die zwei Pole einer Batterie oder einer Steckdose durch ein elektrisch leitfähiges Bauelement miteinander verbunden werden, fließt Strom. Wie groß sich die elektrische Stromstärke dabei einstellt, hängt von der Größe der Spannung und von einer Eigenschaft des leitfähigen Bauelementes ab, die als elektrischer Widerstand bezeichnet wird. In umgekehrter Betrachtungsweise tritt an einem stromdurchflossenen Körper eine Spannung auf, die dann Spannungsabfall oder Spannungsfall genannt wird. Dieser hat am Verbraucher eine Energieabgabe nach außen zur Folge; dagegen ist eine Quellenspannung in der Regel mit einer Energiezufuhr in einen Stromkreis verbunden. Nach der elektro-hydraulischen Analogie kann man sich die Spannung, die die elektrische Ladung durch den Leiter treibt, durch die Druckdifferenz zwischen zwei Stellen einer Rohrleitung vorstellen, die die Flüssigkeit durch das Rohr treibt.

Nach den physikalischen Grundlagen drückt die Spannung die Fähigkeit aus, Ladungen zu verschieben, sodass durch den angeschlossenen Verbraucher ein Strom fließt und Arbeit verrichtet wird. Die elektrische Spannung zwischen zwei Punkten wird definiert als das Linienintegral der elektrischen Feldstärke längs eines festgelegten Weges von dem einen Punkt zum anderen.[4][5] Sie ist zugleich die Differenz der potentiellen elektrischen Energie, die eine Ladung an den zwei Punkten hat, bezogen auf diese Ladung. Das wird auch vereinfachend als „Spannung = Energie pro Ladung“ bezeichnet.[6][7]

Auf „natürliche“ Weise entsteht elektrische Spannung zum Beispiel durch Reibung, bei der Bildung von Gewittern, durch Ionentransport durch eine Biomembran und bei chemischen Redoxreaktionen. Zur technischen Nutzung werden Spannungen meistens durch elektromagnetische Induktion sowie durch Prozesse der Elektrochemie erzeugt.

Elektrische Spannungen gibt es in einem weiten Größenordnungsbereich. Sie können für den Menschen lebensgefährliche Ströme verursachen.

Alessandro Volta, Physiker und Namensgeber der Einheit der Spannung

Definition

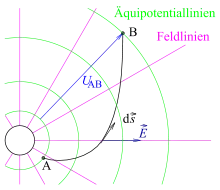
Bewegung einer Ladung im Feld eines Kugelkondensators

Die elektrische Spannung $U_{\mathrm {AB} }$ zwischen zwei Punkten A und B in einem elektrischen Feld mit der Feldstärke ${\vec {E}}$ ist definiert als räumliches Linienintegral längs eines festgelegten Weges von Punkt A zu Punkt B

U_{\mathrm {AB} }=\int _{\mathrm {A} }^{\mathrm {B} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}

.

In diesem Feld befinde sich eine Ladung $q$ , die als so klein angenommen wird, dass sie mit ihrem Feld das vorhandene Feld nicht verändert. Ein mit $q$ geladenes Objekt werde über einen gegebenen Weg von A nach B bewegt. Die Ursache für die Bewegung des Objekts spielt für die Definition keine Rolle.

Auf diese Ladung wirkt eine Kraft ${\vec {F}}=q\;{\vec {E}}$ , sodass bei der Bewegung eine Arbeit $W_{\mathrm {AB} }$ verrichtet wird. Mit „Arbeit gleich Kraft mal Weg“ gilt bei einer vom Ort abhängigen Kraft und Bewegungsrichtung für diese Arbeit $W_{\mathrm {AB} }=\int _{\mathrm {A} }^{\mathrm {B} }{\vec {F}}\cdot \mathrm {d} {\vec {s}}$ .

Damit ergibt sich eine zur Spannungs-Definition oben gleichwertige Aussage

U_{\mathrm {AB} }=\int _{\mathrm {A} }^{\mathrm {B} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}={\frac {1}{q}}\int _{\mathrm {A} }^{\mathrm {B} }{\vec {F}}\cdot \mathrm {d} {\vec {s}}={\frac {W_{\mathrm {AB} }}{q}}

.

Das Vorzeichen von $U_{\mathrm {AB} }$ ergibt sich aus den Vorzeichen von Arbeit und Ladung. Dabei ist die Arbeit negativ, wenn das Feld vom geladenen Objekt bei Verschiebung von A nach B Energie aufnimmt, sie ist positiv, wenn Feldenergie auf die Probeladung übergeht. Aufgrund des Bezugs der Spannung auf $q$ wird diese ein vom Betrag und vom Vorzeichen der Probeladung unabhängiger Parameter des elektrischen Feldes.

Diese Spannungsdefinition gilt für alle elektrischen Felder, also sowohl für Wirbelfelder wie für wirbelfreie (Potential-)Felder. Bei Wirbelfeldern hängt die Spannung $U_{\mathrm {AB} }$ im Allgemeinen vom Weg ab.

Wenn ein elektrisches Feld jedoch ein Quellen- oder Potentialfeld ist (siehe auch konservative Kraft), so ist die Arbeit für die Verschiebung einer Ladung von einem Ort zu einem anderen unabhängig vom Weg zwischen den zwei Orten. Die Spannung ist also nur von den Endpunkten des Integrationsweges abhängig. Das ist in der Elektrostatik und vielen Gebieten der Elektrotechnik der Fall, wodurch der Begriff der elektrischen Spannung erst seine typische praktische Bedeutung erlangt: Man spricht nicht nur von der elektrischen Spannung $U_{\mathrm {AB} }$ zwischen zwei Punkten A und B, sondern von der elektrischen Spannung $U_{\mathrm {AB} }$ zwischen zwei (idealen) Leitern oder Polen A und B. Allgemein gilt dann $U_{\mathrm {AB} }=-U_{\mathrm {BA} }$ .

Elektrisches Potential

Formelzeichen für das elektrische Potential sind $V$ und $\varphi$ .[1][2] Dieses Potential an einem Punkt P im Raum wird mittels der elektrischen Feldstärke ${\vec {E}}$ und des magnetischen Vektorpotentials ${\vec {A}}$ definiert durch[5][8][9]

-{\vec {\nabla }}V={\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}

mit der Anmerkung: Das elektrische Potential ist nicht eindeutig, weil zu einem gegebenen Potential eine beliebige konstante skalare Größe addiert werden kann, ohne seinen Gradienten zu ändern.

Zur Eindeutigkeit wird ein Bezugspunkt P₀ festgelegt, der das Nullpotential $V_{\mathrm {P_{0}} }=0$ erhält. Für die Wahl des Bezugspunkts bestehen in vielen Gebieten Konventionen, sodass er sprachlich oft nicht erwähnt wird. In der Elektrotechnik wird der Bezugspunkt auf dasjenige Leiterstück gelegt, das mit „Masse“ bezeichnet wird; in der Theorie der elektrischen Felder wird der Bezugspunkt oft „ins Unendliche“ gelegt.

Der Integralwert in Bezug auf den Bezugspunkt P₀ wird als elektrisches Potential bezeichnet.

V=-\int _{\mathrm {P_{0}} }^{\mathrm {P} }\left({\vec {E}}+{\frac {\partial {\vec {A}}}{\partial t}}\right)\cdot \mathrm {d} {\vec {s}}

.

Mit den Potentialen $V_{\mathrm {A} }$ und $V_{\mathrm {B} }$ an den Punkten A und B ergibt sich aus der Definition der Spannung

U_{\mathrm {AB} }=\int _{\mathrm {A} }^{\mathrm {B} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}=-(V_{\mathrm {B} }-V_{\mathrm {A} })-\int _{\mathrm {A} }^{\mathrm {B} }{\frac {\partial {\vec {A}}}{\partial t}}\cdot \mathrm {d} {\vec {s}}

.

In einem Potentialfeld ist ${\frac {\partial {\vec {A}}}{\partial t}}=0$ . In den folgenden Ausführungen wird ausschließlich von der elektrischen Spannung in einem Potentialfeld ausgegangen. Dort gelten

{\displaystyle V_{A}=-\int _{\mathrm {P_{0}} }^{\mathrm {A} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}=\int _{\mathrm {A} }^{\mathrm {P_{0}} }{\vec {E}}\cdot \mathrm {d} {\vec {s}}\quad

U_{\mathrm {AB} }=V_{\mathrm {A} }-V_{\mathrm {B} }

.

Die elektrische Spannung zwischen diesen Orten ist folglich gleich der Differenz der elektrischen Potentiale an diesen Orten.

Die Angabe einer Spannung an einem Punkt ist nur im Ausnahmefall möglich, wenn der zweite Punkt für die Spannung aus den Umständen bekannt ist; sonst lässt sich die Spannung immer nur zwischen zwei Punkten angeben. Im Gegensatz dazu hängt das Potential nur vom gewählten Punkt im Raum ab und kann deshalb als ortsabhängige Funktion angegeben werden. Es stellt damit ein Skalarfeld dar, welches (bis auf eine Konstante) aus dem elektrischen Feld ermittelt werden kann und umgekehrt das elektrische Feld eindeutig bestimmt.

Positive Ladungsträger bewegen sich – wenn keine weiteren Kräfte auf sie einwirken – in Richtung der Feldstärke. Weil sie dabei an potentieller Energie verlieren, sinkt in diese Richtung das elektrische Potential. Negativ geladene Objekte bewegen sich dagegen bei Abwesenheit anderer Kräfte entgegen der Feldstärke, in Richtung steigenden Potentials.

Bei einer Verschiebung längs einer Äquipotentiallinie ist das Integral gleich null, weil auf diesem Weg ${\vec {E}}\perp \mathrm {d} {\vec {s}}$ steht, so dass das Skalarprodukt gleich null ist.

Wird eine Ladung von A nach B und über einen beliebig anderen Weg wieder nach A transportiert, so verschwindet im Potentialfeld das Ringintegral über den geschlossenen Umlauf:

\oint {\vec {E}}\cdot \mathrm {d} {\vec {s}}=0

Zählrichtung

Wenn ein Gerät in der Lage ist, eine Spannung aufzubauen, spricht man von einer Spannungsquelle; die Spannung heißt auch Quellenspannung. Anderenfalls ist das Gerät ein elektrischer Verbraucher; die Spannung heißt dann auch Spannungsabfall. Da die Spannung eine skalare Größe ist, legen die in den Darstellungen verwendeten Spannungspfeile lediglich das Vorzeichen fest. Man kann in einer Masche einen Umlaufsinn willkürlich festlegen. Dann ist eine Spannung, deren Pfeil in Richtung des Umlaufs zeigt, positiv und sonst negativ anzusetzen.

Die zwei folgenden Zeichnungen kann man sich jeweils in den Punkten A mit A und B mit B zu einem Stromkreis verbunden denken, wodurch ein elektrischer Strom fließen kann.

Die Richtung der elektrischen Stromstärke wird als diejenige Richtung definiert, in die sich positive elektrische Ladung bewegt, siehe elektrische Stromrichtung. Auch bei Wechselstrom ist eine bestimmte Richtung sinnvoll, wenn Strompfeile die Richtung des Energieflusses anzeigen sollen; die Spannungspfeile ergeben sich sinngemäß wie bei Gleichgrößen.

Die folgende Tabelle zeigt die in der Elektrotechnik weitgehend übliche, im Prinzip willkürliche Richtungsfestlegung gemäß.[10][11] Es gibt durchaus Anwendungen, in denen es angebracht ist, die Spannungsrichtung (bei gegebener Stromrichtung) entgegengesetzt festzulegen, siehe Zählpfeil. So werden etwa in der Elektrokardiographie Spannungen in Richtung steigenden Potentials positiv gewertet, damit die Richtung des Spannungspfeils der Projektion des summierten Dipolmoments entspricht.

Bezeichnung	Schaltbild	Beschreibung
Quellenspannung		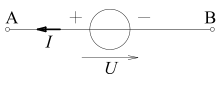Bei Gleichspannung ist die Trennung elektrischer Ladungen eine Ursache für das Auftreten einer elektrischen Quellenspannung zwischen den Polen der Spannungsquelle. Eine positiv gewertete Quellenspannung ist vom Plus- zum Minuspol gerichtet. Wenn aufgrund dieser Spannung ein Strom bei Punkt A herausfließen kann, dann ist die Stromstärke im Inneren der Quelle – positiv gewertet – der Spannung entgegengerichtet.
Spannungsabfall		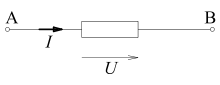Wird beim Fließen des Stromes in einem Leiter die zur Trennung der Ladungen benötigte Energie wieder frei, z. B. in Form von Wärme, spricht man von einem Spannungsabfall. Für einen ohmschen Widerstand (mit einem stets positiven Wert $R$ ) hat die positiv gewertete Stromstärke dieselbe Richtung wie der positiv gewertete Spannungsabfall.

Zusammenhänge

Sowohl die Spannung an sich als auch Zusammenhänge mit anderen Größen im elektrischen Stromkreis werden mithilfe didaktischer Modelle veranschaulicht. Für die Spannung ist vor allem die Analogie zur Höhenenergie (als „Antrieb“ hinabgleitender Kugeln oder Skifahrer) und die Elektro-Hydraulische Analogie (mit der Druckdifferenz zwischen zwei Stellen einer Rohrleitung als „Antrieb“ der Flüssigkeit)[12] verbreitet.[13]

Elektrische Spannung mit Stromstärke

Wenn zwischen zwei Punkten eine elektrische Spannung herrscht, existiert stets ein elektrisches Feld, das eine Kraft auf Ladungsträger ausübt. Befinden sich die Punkte auf einem elektrisch leitfähigen Material, in dem die Ladungsträger beweglich sind, so bewirkt die Spannung eine gerichtete Bewegung der Ladungsträger, und ein elektrischer Strom fließt. Ist die elektrische Stromstärke proportional mit der elektrischen Spannung verknüpft wie bei den meisten Metallen, also wenn

U\sim I,

dann erhält man mit dem Proportionalitätsfaktor $R$ das ohmsche Gesetz

U=R\cdot I.

Wo immer die Proportionalität für jeden Augenblickswert gilt, bei Gleichgrößen wie bei Wechselgrößen, heißt der Faktor Widerstand,[14] zur Betonung seiner Idealform als Konstante auch ohmscher Widerstand.

An Induktivitäten und Kapazitäten ist bei sinusförmiger Spannung die Stromstärke ebenfalls sinusförmig, aber gegenüber der Spannung ist die Stromstärke in ihrem Phasenwinkel verschoben. Das ohmsche Gesetz gilt bei diesen nicht für die Augenblickswerte, aber für die Effektivwerte und Scheitelwerte. Insoweit zählt ein solches Bauelement als linearer Widerstand. Der Proportionalitätsfaktor heißt hierbei Scheinwiderstand $Z$ . In Blick auf Augenblickswerte lässt sich zur Beschreibung ein ohmsches Gesetz der Wechselstromtechnik verwenden, wobei hier die komplexe Impedanz ${\underline {Z}}$ des Bauelements den Proportionalitätsfaktor liefert

{\underline {U}}={\underline {Z}}\cdot {\underline {I}}.

Nichtlineare Bauelemente, bei denen der Widerstand von der Momentanspannung abhängt, gehorchen entsprechend komplizierteren Gesetzen, beispielsweise bei der idealen Diode der Shockley-Gleichung.

Elektrische Spannung mit Leistung und Energie

Die elektrische Ladung kann als Eigenschaft eines Elementarteilchens und damit als quantisierte Größe angesehen werden oder außerhalb atomarer Strukturen in der Regel als stetige und differenzierbare Größe (siehe Elektrische Ladung#Quantencharakter). Beim Durchfluss einer Ladungsmenge $\mathrm {d} Q$ durch einen Widerstand wird infolge der Verschiebungsarbeit eine Energie $\mathrm {d} W$ umgesetzt. Aus der Definitionsgleichung für die Spannung

U={\frac {\mathrm {d} W}{\mathrm {d} Q}}

und aus dem Zusammenhang zwischen Ladung $Q$ und elektrischer Stromstärke $I$

I={\frac {\mathrm {d} Q}{\mathrm {d} t}}

ergibt sich

U\cdot I={\frac {\mathrm {d} W}{\mathrm {d} Q}}\cdot {\frac {\mathrm {d} Q}{\mathrm {d} t}}={\frac {\mathrm {d} W}{\mathrm {d} t}}\;;\quad \Delta W=\int _{t_{A}}^{t_{B}}U\cdot I\ \mathrm {d} t.

Aus der Definition der Leistung $P$ folgt weiter

P={\frac {\mathrm {d} W}{\mathrm {d} t}}\quad \Rightarrow \quad P=U\cdot I,

und speziell bei ohmschen Widerständen mit $I={\frac {U}{R}}$ ergibt sich

{\displaystyle P={\frac {U^{2}}{R}}\quad

Elektrische Spannung am Spannungs- und Stromteiler

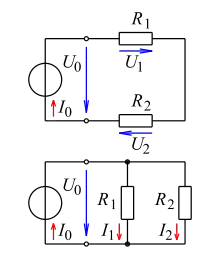
Schaltungen mit Spannungsteiler (oben) und Stromteiler (unten)

Spannungsteiler

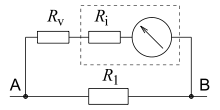
In nebenstehender Abbildung zeigt die obere Schaltung einen Spannungsteiler, der aus genau einem Umlauf besteht. Nach der Maschenregel gilt

U_{1}+U_{2}+(-U_{0})=0.

Die Quellenspannung ist gleich der Summe der Teilspannungen, und bei ohmschen Widerständen ist die Spannung an jedem der Widerstände kleiner als die Quellenspannung. Wie sich die Spannung an den Widerständen aufteilt, ergibt sich daraus, dass sich der Strom in dieser Schaltung nicht verzweigt und somit in der Masche überall mit derselben Stärke $I_{0}$ fließt. Dazu besagt das ohmsche Gesetz

I_{0}={\frac {U_{0}}{R_{1}+R_{2}}}={\frac {U_{1}}{R_{1}}}={\frac {U_{2}}{R_{2}}}.

Damit ist das Verhältnis der Teilspannungen gleich dem Verhältnis der zugehörigen ohmschen Widerstände

{\frac {U_{1}}{U_{2}}}={\frac {R_{1}}{R_{2}}}.

Stromteiler

Die untere Schaltung zeigt einen Stromteiler, bei dem die Quelle und jeder der Widerstände jeweils oben und unten an derselben Leitung liegen, so dass an allen drei Bauteilen dieselbe Spannung $U_{0}$ abfällt.

Messung von elektrischer Spannung

Das zur Messung einer Spannung verwendete Spannungsmessgerät wird parallel zu dem Objekt geschaltet, dessen Spannung gemessen werden soll.

Bei Verwendung eines Drehspulmesswerks, das von seiner Physik her ein Strommessgerät ist, entsteht zur Spannungsmessung eine Stromteiler-Schaltung. Gemessen wird der Strom durch den Innenwiderstand $R_{\text{i}}$ des Messgerätes als Maß für die Spannung. Da jedes Messgerät einen beschränkten Messbereich hat, muss bei Überschreitung des maximal messbaren Wertes über einen Vorwiderstand $R_{\text{v}}$ der Strom vermindert und so der Messbereich erweitert werden.

Die durch die Stromverzweigung entstehende Messabweichung (die Rückwirkungsabweichung durch das Messgerät) wird klein gehalten, wenn $R_{\text{i}}+R_{\text{v}}$ im Vergleich zum Messobjekt $R_{1}$ groß ist. Denn nur so bleibt der Gesamtwiderstand der Messschaltung annähernd unverändert, und die Messschaltung beeinflusst die restliche Schaltung vernachlässigbar wenig. Für den Vergleich wird hier der Faktor $x$ eingeführt

R_{\text{i}}+R_{\text{v}}=x\cdot R_{1}\ .

Bei einer Parallelschaltung addieren sich die Ströme in den Parallelzweigen zum Gesamtstrom und die Leitwerte der Zweige zum Gesamtleitwert.

Spannungsmessung an

R_{1}

mit Drehspulmessgerät

{\frac {1}{R_{\mathrm {ges} }}}={\frac {1}{R_{1}}}+{\frac {1}{R_{\text{i}}+R_{\text{v}}}}

und mit Verwendung von $x$ ergibt das

{\frac {1}{R_{\mathrm {ges} }}}={\frac {1}{R_{1}}}+{\frac {1}{x\cdot R_{1}}}\quad \Rightarrow R_{\mathrm {ges} }={\frac {x}{x+1}}\cdot R_{1}\ .

Wird der Begriff der relativen Messabweichung

f={\frac {x_{\text{a}}-x_{\text{r}}}{x_{\text{r}}}}

mit dem richtigen Wert $x_{\text{r}}$ und dem davon abweichenden Wert $x_{\text{a}}$ auf diese Schaltung übertragen, so ergibt sich

f={\frac {R_{\mathrm {ges} }-R_{1}}{R_{1}}}={\frac {x}{x+1}}-1={\frac {-1}{x+1}}\quad \Rightarrow \quad x={\frac {1}{-f}}-1\ .

Wird für diese stets negative Abweichung beispielsweise gefordert, dass $|f|<1\;\%=0{,}01$ sein soll, so muss $x>99$ sein. Wenn $R_{\text{i}}+R_{\text{v}}$ 100-mal so groß wie $R_{1}$ ist, dann ist $R_{\mathrm {ges} }$ um 1 % kleiner als $R_{1}$ .

Falls der Strom von A nach B aus einer Konstantstromquelle kommt, wird in diesem Fall die Spannung mit einer relativen Abweichung $f$ = −1 % gemessen. Falls zwischen A und B eine Konstantspannungsquelle anliegt, ist $f$ = 0. Bei jeder anderen Speisung liegt die Messabweichung dazwischen.

Wird die relative Abweichung $f$ vorgegeben, die jemand bereit ist zu akzeptieren, so lautet die Forderung an den Widerstand im Messzweig:

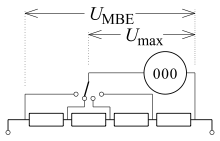
R_{\text{i}}+R_{\text{v}}\geq \left({\frac {1}{|f|}}-1\right)\cdot R_{1}\ .

Spannungsmessung mit digital-elektronischem Messgerät

Bei elektronischen Spannungsmessgeräten (Digitalmessgerät, Oszilloskop oder Kompensations-Messschreiber) ist die Messbereichserweiterung mit einem Vorwiderstand nicht üblich; der Innenwiderstand bei diesen Messgeräten liegt typisch bei 1 bis 20 MΩ in allen Bereichen. Der Vorwiderstand käme in eine Größenordnung, die nicht zuverlässig realisierbar wäre. Stattdessen muss bei Überschreitung des maximal messbaren Spannungswertes $U_{\mathrm {max} }$ ein Spannungsteiler verwendet werden. An einem in der nebenstehenden Schaltung weiter rechts liegenden Abgriff kann eine kleinere Spannung dem anzeigenden Teil zugeführt und so der Messbereichsendwert $U_{\mathrm {MBE} }$ vergrößert werden.

Das Problem, dass das Messgerät wie oben zu $R_{1}$ parallel geschaltet wird, und so der Gesamtwiderstand der Messschaltung verändert wird, ist dasselbe wie oben bei der Messung mit Drehspulmesswerk. Lediglich der je nach Messbereich unterschiedlich große Vorwiderstand $R_{\text{v}}$ entfällt.

Klassifizierung

Zeitabhängigkeit

Zeitabhängige Größen können periodisch zeitabhängige Größen, Übergangsgrößen oder Zufallsgrößen sein.[3] Periodische Spannungen treten in Form einer Wechselspannung oder Mischspannung auf. Nach einem anderen Gesichtspunkt unterscheidet man zwischen harmonischer Spannung (Sinusspannung) und nicht harmonischer Spannung (z. B. Rechteckspannung).[15]

Zu den nicht periodisch zeitabhängigen Größen gehören unter anderem Impulse, Schaltsprünge oder stochastische Größen. Sie lassen sich mathematisch meist nur schlecht oder gar nicht beschreiben.

Spannungen, die ihren Wert in einem größeren zeitlichen Rahmen nicht verändern, werden als Gleichspannung bezeichnet.

Spannungshöhe

Die Europäische Normung unterscheidet drei Spannungsebenen:[16]

Kleinspannung (Wechselspannung ≤ 50 V und Gleichspannung ≤ 120 V)
Niederspannung (Wechselspannung > 50 V bis ≤ 1000 V und Gleichspannung > 120 V bis ≤ 1500 V)
Hochspannung (Wechselspannung > 1000 V und Gleichspannung > 1500 V)

Die Angaben gelten bei Wechselspannung für den Effektivwert, sonst für oberschwingungsfreie Gleichspannung.

Innerhalb der Hochspannung wird weiter unterschieden zwischen Mittelspannung, Hochspannung und Höchstspannung.

Eingeprägte Spannung

Eine Spannung, die sich an einem Bauelement einstellt, hängt ab vom inneren Aufbau der Spannungsquelle. Ihr Quellenwiderstand bildet mit dem Bauelement-Widerstand einen Spannungsteiler. Die sich an der „Last“ der Quelle einstellende Spannung ist in einem ungewissen Maße kleiner als die Leerlaufspannung, solange man die Widerstände nicht kennt. Batterien, Akkumulatoren, fast alle Netzgeräte und sonstige elektronische Stromversorgungsschaltungen liefern eine konstante Spannung – im Sinne von lastunabhängiger Spannung –, beispielsweise 12 V (fest bis zu einer maximal zulässigen Stromstärke). In diesem Fall spricht man von eingeprägter Spannung.

Auch bei Wechselspannung spricht man von eingeprägter Spannung, beispielsweise 230 V im mitteleuropäischen Niederspannungsnetz, wenn sich bei einer Laständerung nur der Strom ändert.

Wechselspannungstechnik

Historischer 2-MVA-Generator (teil-geöffnetes Gehäuse)

Kurzwellen-Funkantenne

Wechselspannung ist definitionsgemäß periodisch und enthält keinen Gleichanteil. Die Wechselspannungstechnik beschäftigt sich hauptsächlich mit Anwendungen in der Energie- und der Nachrichtentechnik.

Die Angaben zur Definition und alle folgenden Größen entsprechen der Normung.[17]

Kennwerte

Zur Beschreibung einer Wechselspannung ist oft die Kenntnis des zeitlichen Verlaufs erforderlich; zu dessen Messung ist ein Oszilloskop notwendig. Daran sind ablesbar:

T

= Periodendauer oder kurz Periode;

bei nicht harmonischen Vorgängen: Periodendauer der Grundschwingung

{\hat {u}}=u_{\mathrm {max} }

= Maximalwert (allgemein), Scheitelwert (bei Wechselspannung)

{\check {u}}=u_{\mathrm {min} }

= Minimalwert

{\underset {{}^{\lor }}{\overset {{}_{\land }}{\!u}}}=u_{\mathrm {max} }-u_{\mathrm {min} }

= Spitze-Tal-Wert

oder elementar zu berechnen:

f=1/T

= Frequenz

\omega =2\pi f

= Kreisfrequenz (bei Sinusform)

Bei der Vielzahl zeitlicher Verläufe von Spannungen mit unterschiedlichen Kurvenformen dienen zu einer ersten Bewertung, wie sie in vergleichbaren Anwendungen wirken, gemittelte Werte, die mit einfacheren Spannungsmessgeräten bestimmbar sind. Ferner gibt es mehrere Bewertungsfaktoren.

Gemittelte Werte

Bezeichnung	Formel	Beschreibung
Gleichwert	${\overline {u}}=U_{-}={\frac {1}{T}}\int _{0}^{T}u(t)\mathrm {d} t$	Als Gleichwert einer Spannung bezeichnet man den arithmetischen Mittelwert dieser Spannung im Zeitintervall der Periode $T$ . Bei Wechselspannung ist dieser definitionsgemäß gleich null.
Gleichrichtwert	${\overline {\left\|u\right\|}}={\frac {1}{T}}\int _{0}^{T}\left\|u(t)\right\|\mathrm {d} t$	Als Gleichrichtwert einer Spannung bezeichnet man den arithmetischen Mittelwert des Betrages dieser Spannung.
Effektivwert	$U={\sqrt {{\frac {1}{T}}\int _{0}^{T}{u^{2}(t)\ \mathrm {d} t}}}$	Unter dem Effektivwert versteht man den quadratischen Mittelwert dieser Spannung.

Bewertungsfaktoren

Bezeichnung	Formel	Beschreibung	Bewertung
Scheitelfaktor	$k_{s}={\frac {\hat {u}}{U}}$	Der Scheitelfaktor (auch Crestfaktor genannt) beschreibt das Verhältnis zwischen Scheitelwert und Effektivwert einer elektrischen Wechselgröße.	Je größer der Scheitelfaktor ist, desto „bizarrer“ ist der Spannungsverlauf; $k_{s}\geq 1$
Formfaktor	$k_{f}={\frac {U}{\overline {\|u\|}}}$	Der Formfaktor bezeichnet das Verhältnis von Effektivwert zu Gleichrichtwert eines periodischen Signals.	Je größer der Formfaktor ist, desto „bizarrer“ ist der Spannungsverlauf; $k_{f}\geq 1$
Schwingungsgehalt	$s={\frac {U_{\sim }}{U}}$	Bei Mischspannung bezeichnet man als Schwingungsgehalt das Verhältnis des Effektivwertes des Wechselspannungsanteils $U_{\sim }$ zum Effektivwert der Gesamtspannung $U={\sqrt {{U_{-}}^{2}+{U_{\sim }}^{2}}}$ .	Je kleiner der Schwingungsgehalt ist, desto mehr nähert sich die Spannung einer Gleichspannung an; $0\leq s\leq 1$
Welligkeit	$w={\frac {U_{\sim }}{\|U_{-}\|}}$	Bei Mischspannung bezeichnet man als Welligkeit das Verhältnis der Effektivwertes des Wechselspannungsanteils zum Betrag des Gleichwertes.	Je kleiner die Welligkeit ist, desto mehr nähert sich die Mischspannung einer Gleichspannung an; $0\leq w<\infty$
Klirrfaktor	$k_{k}={\frac {\sqrt {U^{2}-U_{1}^{2}}}{U}}$	Bei nichtharmonischen Schwingungen gibt der Klirrfaktor an, in welchem Maße Oberschwingungen, die eine sinusförmige Wechselgröße überlagern, Anteil am Gesamtsignal haben. $U$ = Effektivwert der Gesamtspannung; $U_{1}$ = Effektivwert ihrer Grundschwingung.	Je kleiner der Klirrfaktor ist, desto „reiner“ ist die Schwingung sinusförmig; $0\leq k_{k}<1$

Harmonische Wechselspannung

In der Elektrotechnik hat die Sinusfunktion, die auch als harmonische Funktion bezeichnet wird, neben allen anderen möglichen Funktionen die größte Bedeutung. Gründe hierfür werden unter Wechselstrom aufgeführt.

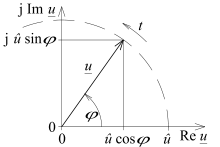
Rotierender Spannungszeiger in der komplexen Ebene als Modell einer harmonischen Wechselspannung

Zur mathematischen Beschreibung verwendet man die Darstellung als reellwertige Größe

u(t)={\hat {u}}\;\sin(\omega t+\varphi _{u})

oder

u(t)={\hat {u}}\;\cos(\omega t+\varphi _{u})

oder die – vielfach Berechnungen vereinfachende – Darstellung als komplexwertige Größe

{\underline {u}}(t)={\hat {u}}\ \mathrm {e} ^{\mathrm {j} \varphi (t)}={\hat {u}}\,(\cos \varphi (t)+\mathrm {j} \,\sin \varphi (t))

mit $\varphi (t)=\omega t+\varphi _{u}$ = Phasenwinkel; $\varphi _{u}$ = Nullphasenwinkel; $\mathrm {j}$ = imaginäre Einheit ( $\mathrm {j} ^{2}=-1$ )

Als gemittelte Werte ergeben sich unabhängig von Frequenz und Nullphasenwinkel

Gleichrichtwert der Sinusspannung: ${\overline {\left|u\right|}}={\frac {2}{\pi }}\;{\hat {u}}\approx 0{,}6366\cdot {\hat {u}}$

Effektivwert der Sinusspannung: $u_{\mathrm {eff} }={\frac {1}{\sqrt {2}}}\;{\hat {u}}\approx 0{,}7071\cdot {\hat {u}}$

Gefahren

Internationales Warnsymbol vor gefährlicher elektrischer Spannung

Obwohl für die Auswirkungen eines Stromunfalls die Stromstärke pro Körperfläche, also die Stromdichte, sowie deren Einwirkdauer verantwortlich sind, wird in der Regel die Spannung als Hinweis auf mögliche Gefahren angegeben. Bei Spannungsquellen lässt sich diese Spannung einfach beziffern, während die Stromstärke – beispielsweise durch einen Körper, der mit Leitungen in Kontakt kommt – nur indirekt (in einfachen Fällen mithilfe des ohmschen Gesetzes) berechnet werden kann und stark von der konkreten Situation abhängt (beispielsweise vom Körperwiderstand und der Frequenz). Außerdem bestimmt die Höhe der Spannung den Mindestabstand zu blanken, nicht isolierten elektrischen Leitern wegen potentiellen Überschlags.

Die allgemeine Regel lautet: 50 V Wechselspannung oder 120 V Gleichspannung sind jeweils die höchstzulässige Berührungsspannung.[18]

Spannung in der Chemie und Kernphysik

Elektrische Spannungen in der Elektrochemie liegen meist im unteren einstelligen Voltbereich. Für jede Reaktion besteht ein Standardpotential als Differenz der Elektrodenpotentiale. Deren Konzentrationsabhängigkeiten werden mit der Nernst-Gleichung beschrieben.

Elektrische Spannungen in der Kernphysik werden zur Beschleunigung von elektrisch geladenen Teilchen verwendet, die Spannungen liegen im Hochspannungsbereich von einigen 10 Kilovolt bis zu einigen Megavolt. Die in diesem Zusammenhang verwendete Maßeinheit „Elektronenvolt“ dagegen ist keine Spannungs-, sondern eine Energieeinheit: 1 Elektronenvolt (auch Elektronvolt; Einheitenzeichen eV) entspricht der (kinetischen) Energie der Elementarladung $e$ (z. B. eines einzelnen Elektrons), das in einem elektrischen Feld durch eine Spannung von 1 Volt beschleunigt wurde.

Literatur

Gert Hagmann: Grundlagen der Elektrotechnik. Aula-Verlag, Wiebelsheim 2006, ISBN 3-89104-707-X.
Helmut Lindner, Harry Brauer, Constans Lehmann: Taschenbuch der Elektrotechnik und Elektronik. 8., neu bearb. Auflage. Fachbuchverlag, Wien u. a. 2004, ISBN 3-446-22546-3.
Ralf Kories, Heinz Schmidt-Walter: Taschenbuch der Elektrotechnik. 7., erw. Auflage. Deutsch, Frankfurt am Main 2006, ISBN 3-8171-1793-0.
Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller: Grundlagen der Elektrotechnik. 20., überarb. Auflage. Teubner, Stuttgart u. a. 2005, ISBN 3-519-66400-3.
Siegfried Altmann, Detlef Schlayer: Lehr und Übungsbuch Elektrotechnik. 3., bearb. Auflage. Fachbuchverlag, Wien u. a. 2003, ISBN 3-446-22683-4.
Manfred Albach: Periodische und nichtperiodische Signalformen. Grundlagen der Elektrotechnik. Pearson Studium, München u. a. 2005, ISBN 3-8273-7108-2.

Weblinks

Wiktionary: Spannung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Anschauliche Erläuterung des Spannungsbegriffs mit einem Wassermodell
Elektrische Spannung auf Schülerniveau erklärt (LEIFI)
Multimediale Online-Lektion Elektrische Spannung (Telekolleg Physik 16, Bayerischer Rundfunk)

Einzelnachweise und Anmerkungen

Anmerkung: Hier besteht allerdings die Gefahr, dass das Formelzeichen V mit dem zugehörigen Einheitenzeichen V für Volt verwechselt wird.

DIN 1304-1:1994 Formelzeichen.
EN 60027-1:2007 Formelzeichen für die Elektrotechnik.
DIN 5483-2:1982 Zeitabhängige Größen.
IEC 60050, siehe DKE Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE: Internationales Elektrotechnisches Wörterbuch Eintrag 121-11-27.
DIN 1324-1:2017 Elektromagnetisches Feld – Teil 1: Zustandsgrößen.
Moeller: Grundlagen der Elektrotechnik. Springer-Verlag, 2013, ISBN 978-3-663-12156-5, S. 139 (google.com).
Ekbert Hering, Rolf Martin, Martin Stohrer: Physik für Ingenieure. Springer Vieweg, 12. Aufl. 2016, S. 241
IEC 60050, siehe Internationales Elektrotechnisches Wörterbuch Eintrag 121-11-25.
EN 80000-6:2008 Größen und Einheiten – Teil 6: Elektromagnetismus; Eintrag 6–11.
DIN EN 60375:2004 Vereinbarungen für Stromkreise und magnetische Kreise; Kap. 6.1 und 6.2.
IEC 60050, siehe Internationales Elektrotechnisches Wörterbuch Eintrag 131-12-04.
Helmut Haase, Heyno Garbe, Hendrik Gerth: Grundlagen der Elektrotechnik. 3. Auflage. Schöneworth, 2009, ISBN 978-3-9808805-5-8, 8.8 Analogie von Strom- und Pumpenkreis.
Weitere Veranschaulichungen siehe z. B. Jan-Philipp Burde (2018): Konzeption und Evaluation eines Unterrichtskonzepts zu einfachen Stromkreisen auf Basis des Elektronengasmodells; Studien zum Physik- und Chemielernen, Band 259, Logos-Verlag, Berlin, ISBN 978-3-8325-4726-4, Online, S. 62–72
EN 80000-6; Eintrag 6–46.
DIN 1311-1:2000 Schwingungen und schwingungsfähige Systeme.
DIN EN 50110-1:2005 (VDE 0105-1) Betrieb elektrischer Anlagen.
DIN 40110-1:1994 Wechselstromgrößen.
VDE 0100, vergleiche dazu TAEV 2004 IV/1.1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[4] Anmerkung: Hier besteht allerdings die Gefahr, dass das Formelzeichen V mit dem zugehörigen Einheitenzeichen V für Volt verwechselt wird.

[D04-1] DIN 1304-1:1994 Formelzeichen.

[D27-1-2] EN 60027-1:2007 Formelzeichen für die Elektrotechnik.

[D83-3] DIN 5483-2:1982 Zeitabhängige Größen.

[5] IEC 60050, siehe DKE Deutsche Kommission Elektrotechnik Elektronik Informationstechnik in DIN und VDE: Internationales Elektrotechnisches Wörterbuch Eintrag 121-11-27.

[D24-6] DIN 1324-1:2017 Elektromagnetisches Feld – Teil 1: Zustandsgrößen.

[Moeller2013-7] Moeller: Grundlagen der Elektrotechnik. Springer-Verlag, 2013, ISBN 978-3-663-12156-5, S. 139 (google.com).

[8] Ekbert Hering, Rolf Martin, Martin Stohrer: Physik für Ingenieure. Springer Vieweg, 12. Aufl. 2016, S. 241

[9] IEC 60050, siehe Internationales Elektrotechnisches Wörterbuch Eintrag 121-11-25.

[10] EN 80000-6:2008 Größen und Einheiten – Teil 6: Elektromagnetismus; Eintrag 6–11.

[11] DIN EN 60375:2004 Vereinbarungen für Stromkreise und magnetische Kreise; Kap. 6.1 und 6.2.

[IEV-12] IEC 60050, siehe Internationales Elektrotechnisches Wörterbuch Eintrag 131-12-04.

[13] Helmut Haase, Heyno Garbe, Hendrik Gerth: Grundlagen der Elektrotechnik. 3. Auflage. Schöneworth, 2009, ISBN 978-3-9808805-5-8, 8.8 Analogie von Strom- und Pumpenkreis.

[14] Weitere Veranschaulichungen siehe z. B. Jan-Philipp Burde (2018): Konzeption und Evaluation eines Unterrichtskonzepts zu einfachen Stromkreisen auf Basis des Elektronengasmodells; Studien zum Physik- und Chemielernen, Band 259, Logos-Verlag, Berlin, ISBN 978-3-8325-4726-4, Online, S. 62–72

[15] EN 80000-6; Eintrag 6–46.

[16] DIN 1311-1:2000 Schwingungen und schwingungsfähige Systeme.

[17] DIN EN 50110-1:2005 (VDE 0105-1) Betrieb elektrischer Anlagen.

[D110-18] DIN 40110-1:1994 Wechselstromgrößen.

[19] VDE 0100, vergleiche dazu TAEV 2004 IV/1.1.