Linienspektrum

Ein Linienspektrum ist ein physikalisches Spektrum, das voneinander getrennte (diskrete) Stellen erhöhter Intensität, sogenannte Spektrallinien, zeigt. Diese Stellen können unter Umständen neben oder überlagert mit kontinuierlichen Anteilen auftreten.

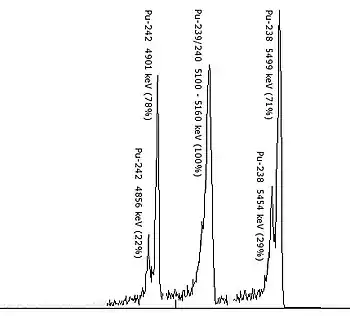
Alphaspektrum der Plutoniumisotope ²⁴²Pu, ²³⁹Pu/²⁴⁰Pu und ²³⁸Pu

Lichtspektren können Absorptions- oder Emissionslinien zeigen. Auch Teilchenstrahlung kann ein Linienspektrum haben; die Teilchen haben dann diskrete kinetische Energien, wie beispielsweise bei der Alphastrahlung.

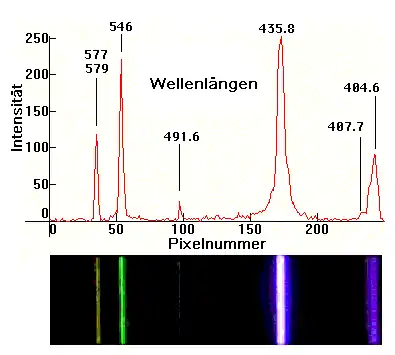
Spektrum einer Niederdruck-Quecksilberdampflampe. Obere Aufnahme mit einem 256-Pixel-Zeilensensor. Untere Aufnahme mit einer Kamera

Ursprung der Linien in Licht- und Röntgenspektren

Jedes Material und jedes Atom oder Molekül hat charakteristische, diskrete Energieniveaus, auf denen sich Elektronen „aufhalten“ können. Der Übergang von einem auf ein anderes Energieniveau erfolgt durch Aufnahme (Übergang vom tieferen auf höheren Zustand) oder Abgabe (Übergang vom höheren in tieferen Zustand) eines Photons mit der Energie

E=h\cdot \nu

(mit der Frequenz $\nu$ der Strahlung und dem Planckschen Wirkungsquantum $h$ ). Die Energiedifferenz zwischen den Energieniveaus entspricht genau der Energie des Photons, und die Energie eines Photons wiederum bestimmt zusammen mit der Lichtgeschwindigkeit $c$ dessen Wellenlänge

\lambda ={\frac {c}{\nu }}

.

Von allen möglichen Energiezuständen eines Materials sind im Allgemeinen nur wenige Paare von Energiezuständen bevorzugte Absorber oder Emitter.

Wenn sich zwischen einer Strahlungsquelle mit kontinuierlichem Spektrum und einem Spektrometer (etwa zum Messen des Spektrums) ein Material befindet, absorbiert es Photonen derjenigen Energien, die durch die Energiezustände des Materials gegeben sind. Die absorbierten Photonen fehlen dann im beobachteten Spektrum der Quelle; dadurch erscheinen dunkle Absorptionslinien.

Ein angeregtes Atom oder Molekül geht nach einer kurzen Zeitspanne wieder in einen tieferen Energiezustand zurück. Dabei wird ein Photon ausgesandt, dessen Energie der Energiedifferenz zwischen höherem und tieferem Energiezustand entspricht. Wenn man dieses Material von der Seite, das heißt ohne dass die Strahlungsquelle sichtbar ist, beobachtet, erscheinen diese Photonen einer bestimmten Energie (und somit Wellenlänge) als Emissionslinien im Spektrum.

Informationsgewinn aus Linienspektren

Linienspektren von Atomen waren eine wichtige Informationsquelle für die Entdeckung der Quantenmechanik. Das besonders einfache Spektrum des Wasserstoffatoms gab den Anstoß zum Bohrschen Atommodell. Genauere Untersuchungen der Wasserstoff-Spektren machten später deutlich, dass dieses Atommodell die Wirklichkeit nur unzureichend beschreibt und die Theorien von Werner Heisenberg und Wolfgang Pauli eine genauere Beschreibung liefern.

In der Astronomie sind Linienspektren eine Quelle für Information über das Universum. Die Linienspektren sind charakteristisch für das jeweilige Atom oder Molekül, daher lassen sich aus dem Licht die im All vorkommenden Elemente bestimmen. Auf diese Weise wurde zum Beispiel das Helium zunächst auf der Sonne gefunden, bevor man es auch auf der Erde nachweisen konnte.

Linienspektren haben in der Astronomie eine weitere Anwendung: Da die exakten Energien der Spektren der Elemente bekannt sind und die Elemente anhand des Musters der Linien identifiziert werden können, kann man aus dem Linienspektrum eines Sterns die Rotverschiebung seines Lichts bestimmen. Für nähere Objekte erlaubt dies über den Doppler-Effekt eine Bestimmung der Geschwindigkeit des Objekts in Richtung der Sichtlinie. Dieser Sachverhalt findet bei der Suche nach Exoplaneten als Radialgeschwindigkeitsmethode Anwendung. Für weiter entfernte Objekte erhält man aus der Rotverschiebung aufgrund des Hubble-Gesetzes die Entfernung des Objekts von der Erde.

Die Linienspektren der Gammastrahlung erlauben in vielen Fällen den Nachweis geringer Mengen eines Radionuklids.

Linienspektrum in der Akustik und Elektrotechnik

Ein akustisches Linienspektrum enthält eine oder mehrere diskrete Frequenzen (DIN 13320). Periodische Schallvorgänge erzeugen ein Linienspektrum, aperiodische oder stochastische Schallvorgänge ein kontinuierliches Spektrum (Bandenspektrum). Ein typisches Beispiel für ein Linienspektrum ist etwa das Klangspektrum oder ein periodisches Signal (Spannung bzw. Strom).

Beim Linienspektrum wird jede Teilfrequenz des Signals durch eine diskrete Spektrallinie symbolisiert. Die Frequenz wird durch die Lage auf der Abszisse (Frequenzachse) dargestellt; die Länge einer solchen Linie stellt die Amplitude der Schwingung (Amplitudenspektrum) oder die Stärke eines Schallvorgangs (Pegelspektrum) dar. Die Frequenzskala wird in der Regel logarithmisch unterteilt. Jede Spektrallinie (konstante Frequenz, konstante Amplitude) stellt für sich eine ideale harmonische (d. h. sinusförmige) Schwingung (also z. B. Spannung) dar. Das zugehörige Phasenspektrum stellt die Phaseninformation (Nullphasenwinkel) z. B. der Amplituden einer Spannung oder eines Stromes dar. Amplituden- und Phasenspektrum zusammen beschreiben ein Signal äquivalent zu seiner Zeitbereichsdarstellung.

Literatur

Dieter Meschede: Gerthsen Physik. 23. Auflage, Springer-Verlag, Berlin Heidelberg New York 2006, ISBN 978-3-540-25421-8.
Thomas Görne: Tontechnik. 1. Auflage, Carl Hanser Verlag, Leipzig 2006, ISBN 3-446-40198-9.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.