Feder (Technik)

Eine Feder ist ein in der Regel metallisches technisches Bauteil, das sich im praktischen Gebrauch ausreichend elastisch verformen lässt. Die am meisten verwendete Feder ist die Schraubenfeder, ein in Schraubenform gewickelter Draht.

Schraubenfeder eines Kugelschreibers (Schraubendruckfeder)

Schraubenzugfeder

Wirkprinzipien

Die elastische Verformung von Federn ist meistens eine Biegung oder eine Torsion. Ein Biegemoment führt zu Biegespannungen, oder ein Torsionsmoment führt zu Torsionsspannungen. Folglich sind Federn primär entweder Biegefedern oder Torsionsfedern. Die anderen Verformungen –

Dehnung (oder Stauchung) unter Normalkraft (Zugkraft (oder Druckkraft)), die zu Zugspannung (oder Druckspannung) führt und
Scherung unter Querkraft, die zu Scherspannung führt –

treten immer gleichzeitig, aber in untergeordnetem Maße auf. Die Biegung ist keine eigenständige Verformung, sondern einerseits eine Dehnung (im Bogen-äußeren Teil des Querschnitts) und andererseits eine Stauchung (im Bogen-inneren Teil des Querschnitts).

Bei Biegung und Torsion ist der Verformungsweg (oder -winkel), der aus der nicht durchgehend gleich starken Beanspruchung des Querschnitts resultiert (Beanspruchung im Zentrum gleich Null), relativ hoch, weshalb Biege- und Torsionsfedern bevorzugt technisch angewendet werden.

Geschichte

oben: Latènezeitliche Certosa-Fibel; unten: römische Zwiebelknopffibel

Einfach geformte federnde Körper, wie bspw. der hölzerne Bogen zum Abschießen von Pfeilen, wurden von den Menschen bereits in urgeschichtlichen Tagen verwendet. Im Bronzezeitalter gab es in vielen Kulturen bereits komplexere federnde Gebilde wie die Pinzette und die Fibel. Ktesibios von Alexandrien stellte Bronze mit besonderen federelastischen Eigenschaften als Legierung mit erhöhten Zinn-Anteil her, die nach dem Gießen durch Hämmern gehärtet wurde.

Vorspannbare (aufziehbare) aus Blechstreifen gewickelte Federn dienen seit dem frühen fünfzehnten Jahrhundert zum Antrieb von Tischuhren, ab dem Übergang zum sechzehnten Jahrhundert auch von Taschenuhren. Die Spiralfeder in der taktgebenden Unruh wurde ab 1673 von Salomon Coster in Taschenuhren eingebaut (Erfinder war Christiaan Huygens).

Im Jahr 1676 formulierte der britische Physiker Robert Hooke das der elastischen Verformung zugrunde liegende Hookesche Gesetz: Die Verformung ist der Belastung proportional.

Anwendungen

Alle Anwendungen der Feder beruhen auf deren Vermögen, potentielle Energie zu speichern.[1]

Antriebsenergie: Die Energie einer vorgespannten (aufgezogenen) Feder dient zum Antrieb beweglicher Geräte wie mechanische Uhren. Der Antrieb hört auf, wenn die Feder wieder entspannt ist.
Rückstellkraft: Federkraft als Gegenkraft zum Beispiel in Federwaagen, Drehspulmesswerken oder Drehmomentschlüsseln.
kraftschlüssige Verbindung: Für die bei einem Reibschluss erforderliche Normalkraft wird oft die Rückstellkraft einer vorgespannten Feder verwendet, zum Beispiel in Reibungskupplungen oder Türfeststellern.
Ausweichendes Teil bei Formänderung anderer Bauteile: Bauteile, deren Abmessungen sich im Betrieb ändern, werden oft federnd ausgebildet oder mit einer Feder kombiniert eingebaut, um Zwängungen, etwa bei thermischer Ausdehnung oder schädliches Spiel, zum Beispiel bei Verschleiß durch Abrieb zu vermeiden. Verschleiß in einer Reibungskupplung führt nur zu etwas geringerem Anpressen der Reibflächen aufeinander, nicht zur Kontaktunterbrechung. Bei Verwendung einer Dehnschraube wächst die Vorspannung bei Wärmedehnungen in verträglichem Maß. Beim plastischen Nachgeben (Setzen) des mit der Schraube befestigten Teils wird diese nicht locker.
Lastverteilung: Großflächige Lastübertragung zwischen Körpern ist gleichmäßiger, je elastisch nachgiebiger die Körper oder einer der Körper sind. Beispiel ist die Federkernmatratze, bei der mehrere Federn beim Belasten vorgespannt werden.
Teil eines schwingfähigen Feder-Masse-Systems: Kinetische Energie verformt die Feder, wonach diese Energie als potentielle Energie vorliegt. Die Masse schwingt aus, bis alle kinetische in potentielle Energie umgeformt ist. Danach wird die Energieumwandlung gegenläufig, und die Masse schwingt zurück in die entgegengesetzte Endlage.
- Ein Körper wird federnd gelagert, um die Wirkung von Stößen, das sind hohe, kurzzeitig auf ihn wirkende Kräfte, zu mildern. Damit die Schwingung schnell abklingt, wird sie gedämpft, wie zum Beispiel die Federung eines Fahrzeugs mit Stoßdämpfern.
- Das permanente Schwingen eines Körpers wird durch seine Kombination mit einer Feder erreicht, zum Beispiel das der mit einer Feder gekoppelten Unruhe einer mechanischen Uhr. Die Dämpfung durch Reibung in den Drehlagern der Unruhe wird kompensiert, indem dem schwingenden System bei jedem Ausschlag eine kleine Energiemenge aus der Antriebsfeder der Uhr zugeführt wird.

Materialien

Federn werden aus Stahl- (Federstahl) und Kupfer-Legierungen (meistens Berylliumkupfer) hergestellt. Die Halbzeuge sind vorwiegend schmale Bänder und Drähte. Aus anderen elastischen Werkstoffen wie Gummi und faserverstärktem Kunststoff gibt es keine typisierten Federn. Gasdruckfedern sind in der Regel auch Spezialanfertigungen.

Kenngrößen

Federkennlinien
1 progressiv
2 linear
3 degressiv
4 sehr weich, vorgespannt
5 linear mit Knickstelle

Zur Charakterisierung von Federn wird die Federkonstante (Federhärte) oder die Federkennlinie angegeben. Diese beschreiben den Zusammenhang zwischen Verformung (Weg s oder Winkel φ) und Kraft F oder Drehmoment M_t. Die Federkennlinie ist wie das ihr zugrundeliegende Hookesche Gesetz in guter Näherung linear (→ Feder-Konstante, siehe 2 in Abb.). Für besondere Zwecke werden nichtlineare, oft auf besondere Weise verwirklichte nichtlineare Kennlinien benutzt.

Kennlinien-Beispiele:

Gedrückte Gummifedern (Gummiklötze) haben prinzipiell eine progressive Kennlinie (1).
Moderne Sportbögen haben eine degressive Federkennlinie (3). Die Fläche unter der Kennlinie entspricht der gespeicherten Energie. Diese ist bei gleicher Haltekraft größer als bei einer linearen Kennlinie.
Bei einer KFZ-Kupplung soll die Pedalkraft über den Pedalweg nicht zu stark ansteigen (4), wofür eine vorgespannte Membranfeder geeignet ist.
Die Fahrzeugfederung ist häufig progressiv ausgelegt (1), um ein Durchschlagen bei hoher Last zu verhindern, während bei Normallast eine weiche, komfortable Federung gewünscht ist. Die Verhärtung der Feder tritt ein, indem die größeren Windungen sich aufeinander legen und damit die wirksame Federlänge verkürzen. Den gleichen Zweck erfüllt eine zweistufige Wicklung, die etwas einfacher herzustellen ist. Eine Annäherung kann auch erreicht werden, indem zwei unterschiedliche Federn hintereinander gesetzt werden (5).
Unstetige Verläufe entstehen auch bei Blattfedern mit gewölbtem Querschnitt wie dem Knackfrosch (5).

Verformungs-Gleichungen

Biegefeder

Ein in $x$ -Richtung ausgedehnter biegsamer Stab nimmt bei Beanspruchung durch das Biegemoment $M_{y}(x)$ in der $xz$ -Ebene die Krümmung $w''(x)$ an:

w''(x)=-{\frac {M_{y}(x)}{E\cdot I_{y}}}

(

E

: Elastizitätsmodul des Werkstoffs

I_{y}

: Flächenträgheitsmoment bei Biegung um die

y

-Achse)

Torsionsfeder

Der Verdrehwinkel $\phi$ eines Stabs der Länge $L$ bei Beanspruchung mit dem Torsionsmoment $M_{t}$ beträgt:

\phi ={\frac {M_{t}\cdot L}{G\cdot I_{p}}}

(

G

: Schubmodul des Werkstoffs

I_{p}

: polares Flächenträgheitsmoment des Querschnitts)

Biegefedern

Die meisten Biegefedern sind Blattfedern (rechteckiger Querschnitt), Drahtfedern sind in der Unterzahl. Gerade (gestreckte) Biegefedern lassen sich mit der für gerade Balken geltenden Balkentheorie behandeln. Für die überwiegend gekrümmten Biegefedern sind zwei Besonderheiten zu beachten:

Die Spannungsverteilung im Querschnitt ist nicht mehr wie bei den geraden Federn symmetrisch. Die Spannung der konkaven Randfaser ist erhöht, was mit Hilfe von Korrekturfaktoren berücksichtigt werden muss.
Bei der Herstellung der Krümmung wird die zulässige Spannung gemindert, wenn keine Wärmenachbehandlung erfolgt.[2]
Spiralfeder und schwingende Unruh

Spiralfedern

Antriebsfeder einer Paillard-Bolex-Schmalfilmkamera, entspannt

Spiralfedern sind in einer Ebene in Schneckenlinie aufgewickelte und dadurch stark gekrümmte Metallbänder. Sie sind Hauptbestandteil von Uhren mit Federantrieb. Ihr gleichmäßiger Ablauf wird mit mechanischen Hilfseinrichtungen (Hemmung, reibende Drehzahl-Regler) erreicht. Später wurden sie auch in Grammophone, Filmkameras und Telephone mit Wählscheibe eingebaut. In Spielzeugen werden sie Federmotoren, die i. d. R. einfacher konstruiert sind und ungleichmäßig schnell ablaufen oder durch eine Schwungmasse geregelt sind, genannt.

In der Hemmung der mechanischen Uhr ist die Spiralfeder als Unruh-Feder enthalten.[3] Ein besonderer Spiralfeder-Antrieb ist der Rollfeder-Antrieb, bei dem eine Spiralfeder zwischen zwei Gehäusen (Trommeln) hin- und herbewegt wird. In bevorzugter Ausführung hat die Feder in beiden Trommeln unterschiedliche Krümmung und speichert somit mehr Energie als bei einseitiger Krümmung. Beim Aufziehen des Antriebs wird die Feder in der Abtriebsstrommel aufgewickelt. Beim Ablauf zieht sich die Feder in die Vorratstrommel zurück, um ihre ursprüngliche Form anzunehmen, und treibt dabei die Abtriebstrommel an.[4] Dieser Federantrieb wird z. B. zum Aufrollen von Netzkabeln in Staubsaugern benutzt.

Auch in anderen Feder-Antrieben wird die Spiralfeder oft Rollfeder genannt.

Prellfeder

Die Prellfeder am Schlagwerk-Ende unter dem hellen Flachstahl-Bogen ist eine dauerbelastete Blattfeder

Prellfedern gibt es seit dem frühen Mittelalter für den gemeindeweit hörbaren Anschlag an eine Glocke. Sie ermöglicht den Einzelschlag und verhindert dann falschen Nachschlag des Hammers an die Glocke. Die U-förmig abgewinkelte Prellfeder wird „Anschlagfeder“ bezeichnet. Bis ca. 1920 bildete die Prellfeder mit Anschlaghammer das Schlagwerks-Ende der rein mechanischen Räderuhr (Turmuhr) – ab ca. 1930 besitzen elektrische Turmuhren kompakte Hammerwerke, bei denen meistens eine eingespannte Prellfeder integriert ist.

Elliptikfeder

Die seit den gefederten Kutschen in Fahrzeugen verwendeten schwach gebogenen Blattfedern wurden oft paarweise gegeneinander montiert verwendet. Diese Paarung zu einer ellipsenartigen Form ergab die Bezeichnung Elliptikfeder. Die beiden gegenüberliegenden Federn sind meist Federpakete, das heißt aufeinander liegende einzelne Federblätter. Wegen der mittigen Belastung ist das Biegemoment in der Mitte der Federlänge am größten. Dem dreieckigen Momentenverlauf angepasst ist die abgestufte Längsform des Federpakets: Die Länge der zugefügten Blätter nimmt von Stück zu Stück ab.

Dass die Blätter (vorwiegend an den Enden) gegeneinander reiben, kann zur Schwingungs-Dämpfung des Feder-Fahrzeugaufbau-Systems ausgenutzt werden.

Wird die Vollelliptikfeder „beschnitten“, entstehen die ebenfalls angewendeten Formen:
Dreiviertelelliptikfeder (von einem der beiden Pakete ist die Hälfte entfernt, die verbliebene Hälfte ist fest eingespannt),
Halbelliptikfeder (nur eins der ursprünglich beiden Pakete wird verwendet),
Viertelelliptikfeder (von der Halbelliptikfeder ist die Hälfte entfernt, die verbliebene Hälfte ist fest eingespannt, für das an ihr aufgehängte Rad wirkt sie als Kragträger → Cantileverfeder)

Vollelliptikfeder an einer Kutsche
im Classic Car Museum Malta
Dreiviertelelliptikfeder, De Dion-Bouton
Viertelelliptikfeder als Querlenker
Tatsächlich wird i. d. R. eine Halbelliptikfeder eingebaut, deren Hälften für je ein Rad je eine Viertelelliptikfeder sind.

Trapezförmige Blattfeder als Ventil-feder („valve spring“)

Konstruktion einer geschichteten Blattfeder (grün) aus einer doppeltrapezförmigen Feder (blau)

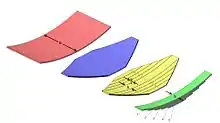
Parabelfeder

Anstatt ein abgestuftes Federpaket zu bilden, kann eine Blattfeder mit parabelförmig von der Mitte zu den Enden hin abnehmender Stärke verwendet werden.

Auf ähnliche Weise wirkt ein in der Fläche trapezförmiges Federblatt (nebenstehende Abbildung).

Wellenfeder

Wellenfedern sind gewellte Ringe aus Flachdraht. Bei Belastung werden die Wellen eingeebnet. Die Federn können zu Paketen übereinander geschichtet als Ersatz für Schraubenfedern dienen (bis halb so hoher Einbauraum, aber gleichem Durchmesser). Einlagig werden sie zum Beispiel in Bajonettverschlüssen und Wellenlagerungen zum axialen Spielausgleich verwendet.

Drahtfeder

Für die oben beschriebenen Anwendungen der Blattfedern (rechteckiger Querschnitt) werden Drähte (runder Querschnitt) wegen der allseitigen Biegenachgiebigkeit kaum verwendet.[5]

Nadelfeder

Die Nadelfeder ist ein gerades oder nur leicht gebogenes flexibles kurzes Drahtstück. Nadelfedern finden unter anderem im Musikinstrumentenbau Verwendung, beispielsweise in der Konstruktion der Klappenmechanik von Holzblasinstrumenten.[6]

Eine Sicherheitsnadel wird durch eine vorgespannte Schenkelfeder geschlossen gehalten.

Wellenfeder

Ausnahmsweise werden Wellenfedern (s. o.) auch aus Draht mit rundem Querschnitt gefertigt.

Schenkelfeder

Schenkelfedern sind schraubenförmig gewickelte (gewundene) Drahtfedern mit abstehenden geraden Enden (Schenkeln). Die Schenkel dienen zur Einleitung des den Draht biegenden Drehmoments. Bei vielen Windungen wird sie auf einem eingesteckten Zylinder oder mit Halbschalen (siehe Wäscheklammer) von außen gegen das sich einstellende Kippmoment geführt

Anwendungsbeispiele sind: Sicherheitsnadel (nebenstehende Abbildung), Wäscheklammer, Mausefalle mit Schlagbügel.

Torsionsfedern

Die meisten Torsionsfedern bestehen aus Stäben oder Draht mit rundem Querschnitt. Andere Querschnitte (quadratisch, rechteckig usw.) sind in der Minderheit. Im Unterschied zu den geraden (gestreckten) Torsionsfedern (Drehstabfeder) sind bei der Behandlung der gewundenen Torsionsfedern (Schraubenfedern) zwei Besonderheiten zu beachten:

Die Spannungsverteilung im Querschnitt ist nicht mehr wie bei den geraden Federn rotationssymmetrisch. Die Spannung ist in den inneren Randfasern gegenüber der in den äußeren erhöht, was mit Hilfe von Korrekturfaktoren berücksichtigt werden muss.
Bei der Herstellung der Krümmung wird die zulässige Spannung gemindert, wenn keine Wärmenachbehandlung erfolgt.[7]

Stabfeder

Beispiele für angewendete Drehstäbe sind das Torsionspendel in mechanischen Uhren, das Torsionsband in Drehspulmessinstrumenten (zur Erzeugung des Reaktionsmomentes und als Lagerelement für die Drehspule) sowie der Stabilisator und die Drehstabfeder zur Fahrzeugfederung.

Schraubenfeder

Bei der Schraubenfeder ist der Federdraht in Schraubenform aufgewickelt (gewunden). Es wird zwischen Schraubenzug- und -druckfedern unterschieden. Die Federn werden in Richtung der Schraubenachse auseinandergezogen oder zusammengedrückt und kurz als Zug- oder Druckfedern bezeichnet. In Schraubenfedern entstehen vorwiegend Torsionsspannungen, nicht Zug- oder Druckspannungen, was fälschlicherweise aus den Bezeichnungen Zug- und Druckfeder gefolgert werden könnte.

Die äußere Kontur weist in den meisten Fällen einen zylindrischen Körper auf, der jedoch für manche Anwendungen gekrümmt (bogenförmig) sein kann, um z. B. ein Drehmoment um eine Achse übertragen zu können: Bogenfeder.

Des Weiteren gibt es kegel- oder tonnenförmige Konturen. Eine Druckfeder in diesen Formen kann stark zusammengedrückt werden, weil die Windungen teilweise ineinander zu liegen kommen: Miniblock-Feder.

Damit die Endwindungen bei Belastung nicht kippen, muss die Kraft mittig eingeleitet werden. Die Ösen der Zugfedern werden so gebogen, dass sie in einer Mittelebene liegen. Bei Druckfedern werden meistens etwa 3/4 der beiden Endwindungen an die je benachbarte Windung angelegt (nichtfedernde Windungen) und rechtwinklig zur Federachse abgeschliffen. So entsteht eine dreiviertelkreisförmige ebene Auflage.[8]

In sicherheitskritischen Anwendungen werden nur zylindrische Druckfedern verwendet, da bei ihnen bei entsprechender konstruktiver Gestaltung der Bruch der Feder dazu führt, dass nur eine Federwindung weniger die Federkraft aufbringt, sodass der Großteil der Federwirkung erhalten bleibt.

Auf gedrückten Schraubenfedern abgestützter Teil eines Eisenbahnwagens
Kegelfedern (Sprungfedern)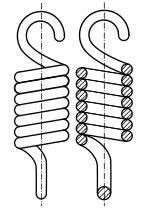
Zugfeder mit mittigen Ösen
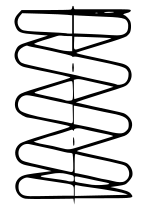Druckfeder, Endwindungen angebogen und abgeschliffen
Bogenfedern und Bogenfedersysteme (Set aus Innen- und Außenbogenfeder)

Die Schraubenfeder ist ein gewundener Drehstab. Die Federwindungen werden in vernachlässigbarem Maße gebogen. Bei ihrer Auslegung wird ausschließlich die Torsionsbeanspruchung beachtet (die Biegebeanspruchung ist vernachlässigbar klein). Die für den Drehstab oben angegebene Gleichung

\phi ={\frac {M_{t}\cdot L}{G\cdot I_{p}}}

ist in der bekannten „Handgleichung“ für Federn aus rundem Draht[9]

c={\frac {F}{s}}={\frac {G\cdot d^{4}}{8\cdot D^{3}\cdot i}}

(mit

c

: Federkonstante,

F

: belastende Kraft,

s

: Federweg,

G

: Schubmodul,

d

: Drahtdurchmesser,

D

: mittlerer Federdurchmesser,

i

: Zahl der federnden Windungen)

für die Behandlung der Schraubenfeder enthalten, wie die folgenden Umstellungen zeigen.

Zwischen Verdrehung $\phi$ und dem Federweg $s$ besteht die Beziehung: $\phi =2s/D$
Das belastende Drehmoment $M_{t}$ wird von der mittig wirkenden Kraft $F$ erzeugt: $M_{t}=F\cdot D/2$ .
Die gestreckte Länge $L$ des gewundenen Drahts ist der Umfang einer Windung $D\pi$ multipliziert mit der Windungszahl $i$ : $L=D\cdot \pi \cdot i$ .
Das polare Flächenträgheitsmoment $I_{p}$ der Kreisfläche ist: $I_{p}=d^{4}\pi /32$ .

Diese vier Ausdrücke in die Drehstab-Gleichung eingesetzt ergibt:

{\frac {2s}{D}}={\frac {(F\cdot D/2)\cdot (D\cdot \pi \cdot i)}{G\cdot (d^{4}\pi /32)}}

,

was mit der gesuchten „Handgleichung“ identisch ist.

Tellerfedern

Spannungen im radialen Querschnitt (19,75 mm × 2 mm, r_a= 30 mm) einer flach gedrückten Tellerfeder aus Stahl, Werte in kp/mm²

Form und Funktion

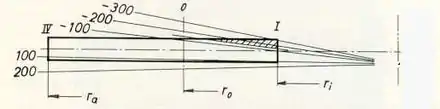
Eine Tellerfeder hat die Form des Mantels eines flachen Kegelstumpfs. Sie wird zwischen ihren Randkreisen elastisch zusammengedrückt (theoretisch, bis sie maximal zu einer ebenen Scheibe verformt ist), wobei sich als Reaktion auf die eingeleiteten Kräfte Normalspannungen (Druck- und Zugspannungen) im Material bilden.[10][11]

Bei üblicher Anordnung von Tellerfedern tritt bei Federwegen über 75 % abweichend von der Rechnung ein progressiver Anstieg der Federkraft ein. Dieser entsteht durch die Verschiebung der Kraftangriffspunkte zu kleineren Hebelarmen, weil sich die Tellerfedern aufeinander oder auf der Anlagefläche abwälzen. Das kann im Federwerkstoff lokale Überbeanspruchungen begünstigen und zu Federbrüchen führen. Deshalb wird empfohlen, den Federweg nur zu ca. 75 bis 80 % auszunutzen. In der DIN 2093 werden aus diesem Grund die Federkräfte nur bei 75 % des Federwegs angegeben. Der nicht-lineare Zusammenhang zwischen Federweg und Federkraft[12] wird unter anderem bei der Verwendung für Kraftfahrzeugkupplungen gezielt ausgenutzt.

Da bei r_i (oben in neben stehender Abbildung) Druckspannungen (-) auftreten, bei r_a aber Zugspannungen (+), ist die verformte Tellerfeder nicht nur ein flacher, sondern entlang einer Mantellinie auch ein leicht gewölbter Kegelstumpf. Bei r₀ ist der Übergang von Druck- zu Zugspannung, dort treten keine Spannungen auf.

Sechs Tellerfedern in „Reihenschaltung“

Zweimal drei Tellerfedern in „Parallelschaltung“, zwei Federpakete in „Reihenschaltung“

Kombinationen

Die einzelne Tellerfeder ist eine relativ harte Feder und wird dementsprechend verwendet. Eine weichere Feder entsteht durch wechselsinniges Aufeinanderschichten der Teller (Reihenschaltung). Das ist ein Anwendungsvorteil, wenn es darum geht, eine weichere Feder aus „Katalog-Teilen“ zu erzeugen. Durch gleichsinniges Aufeinanderschichten (Parallelschaltung) entsteht eine Feder, die härter als die Einzelfeder ist.

Werkstoffe

ausgewiesene Federstähle in Blechform wie C60S (1.1211), C67S (1.1231) und C75S (1.1248) oder 51CrV4 (1.8159)
korrosionsbeständige Stähle wie X10CrNi18-8, X7CrNiAl17-7, X5CrNiMo17-12-2, X5CrNi18-10
warmfeste Stähle wie X22CrMoV121 oder X39CrMo17-1
Kupfer- (CuSn 8, CuBe 2) und Nickel-Legierungen (Nimonic, Inconel, Duratherm)
faserverstärkte Kunststoffe (FVK) in Einzelfällen.

Damit Tellerfedern überhaupt ihre Federeigenschaften (hohe Elastizität bzw. Zähigkeit bei hoher Festigkeit) erhalten, werden Tellerfedern aus üblichen Federstählen nach ihrer Fertigung wärmebehandelt (vergütet) oder direkt aus federhartem Werkstoff gefertigt (Gruppe 1 aus Bandmaterial, s. u.). Nach DIN 2093 muss die Härte zwischen 42 und 52 HRC liegen.

Herstellung

Nach DIN 2093 werden drei Fertigungsgruppen unterschieden:

Gruppe 1: Tellerfedern mit Tellerdicke <1,25 mm: gestanzt oder feingeschnitten aus Bandmaterial
Gruppe 2: Tellerfedern mit Tellerdicke von 1,25 bis 6 mm: gestanzt oder feingeschnitten. Bei gestanzten Tellerfedern werden Innen- und Außendurchmesser nach dem Stanzen gedreht, um Stanzriefen (Kerbwirkung) zu entfernen.
Gruppe 3: Tellerfedern mit Tellerdicke über 6 mm: aus warmgeformten Platinen, die Oberfläche wird komplett gedreht.

Bei kleinen Stückzahlen können Tellerfedern auch aus Bandmaterial gelasert werden.

Normen

DIN EN 16984 – Berechnung (bis 2/2017: DIN 2092)
DIN EN 16983 – Qualitätsanforderungen, Maße (bis 2/2017: DIN 2093)

Anwendungsbeispiele

in Reibungskupplungen zur Erzeugung der Normalkraft (s. auch unten Membranfeder)
in Scheibenbremsen als Rückstellfedern
zum Spielausgleich, z. B. axial bei Kugellagerringen, die mit losem Sitz eingebaut sind
als Antrieb für Leistungsschalter in der Hochspannung.

Andere metallische Federn

Die folgenden Federn sind Ausführungen, die für bestimmte Zwecke entwickelt wurden und kaum allgemein verwendet werden.

Evolutfeder

Die Evolutfeder, auch Pufferfeder, Wickelfeder, Schneckenfeder oder Kegelstumpffeder genannt,[13] ist aus einem flachen Band schraubenförmig überlappt[14] gewickelt. Der dabei entstandene Kegelstumpf wird axial (in Längsrichtung des Bandquerschnitts) elastisch zusammen gedrückt. Der Bandquerschnitt wird tordiert, weshalb eine relativ harte Feder entsteht. Die Federkennlinie ist nichtlinear.

Sie wurde 1846 von John Baillie erfunden und als Eisenbahn-Puffer-Feder verwendet. Sie löste die ältere Schraubenfeder (s. o.) ab und wurde später durch Ringfedern (s. u.) ersetzt.

Heute kommt sie nur noch als Doppel-Evolutfeder (Blechabwicklung ist ein V-förmiger Blechausschnitt) in Gartenscheren häufig vor.

Evolutfeder
Evolutfeder in einem Eisenbahn-Puffer
Doppel-Evolutfeder (Serienschaltung)
Doppel-Evolutfeder in einer Gartenschere

Ringfeder

Ringfeder-Prinzip

Ringfedern in Eisenbahn-Puffer,
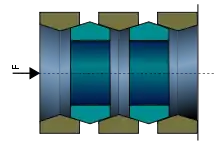
sichtbar sind nur die äußeren Ringe

Die Ringfeder ist heute Standardfeder in Eisenbahn-Puffern. Sie ist äußerst hart. Eine anwendbare Feder ist deshalb ein Stapel aus inneren und äußeren wechselseitig aneinander gereihten Ringen.

Beim Zusammendrücken werden die größeren äußeren Ringe gedehnt und die kleineren inneren Ringe gestaucht. Sie rutschen an den stumpfen kegelförmigen Kontaktstellen ineinander, wobei die federnde Bewegung durch Reibung gedämpft wird. Durch die zusätzliche Dämpfung kann ein Ringfederpaket einen Artnutzungsgrad (η_A) von mehr als eins erreichen.[15]

Kraftfahrzeugkupplung mit Membranfeder

Dosenbarometer mit Dose aus zwei gewellten Membranen

Membranfeder

Membranfedern sind dünne elastische, meist kreisförmige Platten.

Im Automobilbau versteht man unter der Membranfeder die in einer mechanischen Kupplung eines Kraftfahrzeugs verwendete Bauart. Im inneren Bereich ist der leicht kegelige Ring in radiale Zungen aufgelöst. Diese dienen als Betätigungshebel, um zum Lösen der Kupplung den Randbereich umzustülpen. Im nicht umgestülpten Zustand stellt der einer Tellerfeder vergleichbare, vorgespannte Randring die Normalkraft dieser reibschlüssigen Kupplung dar.

Eine Barometerdose besteht aus zwei konzentrisch gewellten kreisförmigen Membranen, die bei Veränderung des Luftdrucks außerhalb der Dose elastisch gegeneinander bewegt werden.

Dehnschraube

Eine Dehnschraube ist relativ lang und hat einen schlanken Schaft. Sie ist ein elastisches Bauteil, das wie eine relativ harte Zugfeder funktioniert, aber nicht als Feder bezeichnet wird.

Nichtmetallische Federn

Gummifeder

Gummifedern sind oft massive Blöcke – manchmal auch Bänder – aus Gummi oder elastischem Kunststoff (Elastomer). Diese Werkstoffe haben eine im Vergleich zu Metall um Größenordnungen kleinere Federhärte bzw. kleineren Elastizitätsmodul. Ihre dämpfenden Eigenschaften sind höher, weshalb man sie häufig zum Entkoppeln von mechanischen und Schallschwingungen verwendet. Sogenannte Silentblöcke haben meistens an zwei gegenüberliegende Seiten anvulkanisierte metallische Teile, mit deren Hilfe sie zwischen zwei gegeneinander gefederte Bauteile befestigt werden. Eine sogenannte Silentbuchse bildet zusammen mit einer metallischen Achse ein Gummilager, d. h. ein elastisches Drehlager, z. B. bei Radaufhängungen von Kraftfahrzeugen.

Bei der Fahrzeugfederung des BMC Mini wurden Gummifedern verwendet. In Kraftfahrzeugen sind neben den eigentlichen (metallischen) Federn Zusatzfedern aus Polyurethan (PUR) oder Microcellular Urethane (MCU) für die Endanschläge der Radaufhängungen zu finden. Es handelt sich hier um einen Kunststoffschaum, der unter Last komprimiert wird. Die Charakteristik einer solchen Zusatzfeder wird maßgeblich durch die Formgebung, sowie durch zusätzliche Stützelemente wie Kunststoffringe bestimmt. Der gängige Werkstoff der Gummifedern ist nicht komprimierbar. Das Dickerwerden eines gedrückten Gummiblocks darf am Einbauort nicht behindert werden.

Luftfeder, geschnitten
mit Schlauchrollbalg

Luftfeder

Bei einer Luftfeder wird die Kompressibilität von Luft ausgenutzt. Einfache Beispiele sind die Luftmatratze und der Luftreifen, ein komplexeres sind die zur Fahrzeugfederung verwendeten Systeme.

Bei Fahrzeugen kommen folgende Vorteile im Vergleich mit metallischen Federn zum Tragen:

Feinfühliges Ansprechen, da fast keine Eigendämpfung.
Vorwählbare und/oder automatisch einstellbare Vorspannung mittels Kompressor an Bord: Dadurch kann die Höhe des Fahrzeugkörpers eingestellt, bzw. unabhängig von der Zuladung gehalten werden. Zu beachten ist allerdings, dass die Federung bei großer Vorspannung härter wird.

Gasdruckfeder

Gasdruckfedern sind abgeschlossene gasgefüllte Federn mit erhöhtem Innendruck (Vorspannung). Sie werden beispielsweise an der Kofferraumklappe bei Automobilen und in gefederten Bürostühlen verwendet.

Siehe auch

Steifigkeit, Elastizitätsmodul, Schubmodul
Gummimotor (Gummiband als Federspeicher)
Federspeicher (Federspeicherbremse)
Federwerk (Antrieb, besonders von mechanischen Uhren)
Bimetalle werden gelegentlich als Bimetallfeder bezeichnet.
Slinky (Schraubenfeder als Spielzeug)

Weblinks

Commons: Feder – Album mit Bildern, Videos und Audiodateien

Verband der deutschen Federnindustrie, mit bebilderter Federtypenliste
Mechanical spring calculators, Berechnung von mechanischen Federn (englisch)

Einzelnachweise

Siegfried Hildebrand: Feinmechanische Bauelemente. Hanser 1968, S. 289, Speicherelemente: Federn.
Hildebrand, 1968, S. 299.
Helmut Kahlert, Richard Mühe, Gisbert L. Brunner: Armbanduhren: 100 Jahre Entwicklungsgeschichte. Callwey, München 1983; 5. Auflage ebenda 1996, ISBN 3-7667-1241-1, S. 36–38.
Hildebrand, 1968, S. 306–308.
Hildebrand, 1968, S. 309.
Günter Dullat: Holzblasinstrumentenbau. In: Edition Moeck. Band 4040. Moeck, 1990, ISBN 978-3-87549-032-9, S. 52 (google.de [abgerufen am 22. Oktober 2017]).
Hildebrand, 1968, S. 315.
Bei der Federung von Fahrzeugen werden schraubenförmig endende Druckfedern oft in Tellern mit schraubenförmiger Vertiefung im Boden gestützt. Lange Druckfedern brauchen eine Führung, damit sie nicht ausknicken können.
Bosch: Kraftfahrtechnisches Taschenbuch. 19. Auflage. VDI-Verlag, 1984, S. 228.
F. Dubois: Über die Festigkeit der Kegelschale. Dissertation an der ETH Zürich, 1913.
P. Bühl: Spannungsberechnung von Tellerfedern. DRAHT 22 (1971) 11, S. 760–763.
Neue Kupplungen für Trabant 601 und Wartburg 353. In: Kraftfahrzeugtechnik 4/1969, S. 120–121.
Bischoff (ein Federhersteller): Technische Zeichnung (Blechabwicklung und zwei Ansichten) einer Kegelstumpffeder .
In der Art einer Bandage um Finger, Arm oder Bein.
Albert Albers: Grundlagen der Berechnung und Gestaltung von Maschinen. In: Waldemar Steinhilper (Hrsg.): Konstruktionselemente des Maschinenbaus. 8. Auflage. Band 1. Springer-Verlag, Berlin/Heidelberg 2012, ISBN 978-3-642-24300-4, 5.1.2.3 Nutzungsgrad, S. 206, 224.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[:0-1] Siegfried Hildebrand: Feinmechanische Bauelemente. Hanser 1968, S. 289, Speicherelemente: Federn.

[HI299-2] Hildebrand, 1968, S. 299.

[3] Helmut Kahlert, Richard Mühe, Gisbert L. Brunner: Armbanduhren: 100 Jahre Entwicklungsgeschichte. Callwey, München 1983; 5. Auflage ebenda 1996, ISBN 3-7667-1241-1, S. 36–38.

[4] Hildebrand, 1968, S. 306–308.

[5] Hildebrand, 1968, S. 309.

[6] Günter Dullat: Holzblasinstrumentenbau. In: Edition Moeck. Band 4040. Moeck, 1990, ISBN 978-3-87549-032-9, S. 52 (google.de [abgerufen am 22. Oktober 2017]).

[HI315-7] Hildebrand, 1968, S. 315.

[8] Bei der Federung von Fahrzeugen werden schraubenförmig endende Druckfedern oft in Tellern mit schraubenförmiger Vertiefung im Boden gestützt. Lange Druckfedern brauchen eine Führung, damit sie nicht ausknicken können.

[9] Bosch: Kraftfahrtechnisches Taschenbuch. 19. Auflage. VDI-Verlag, 1984, S. 228.

[10] F. Dubois: Über die Festigkeit der Kegelschale. Dissertation an der ETH Zürich, 1913.

[11] P. Bühl: Spannungsberechnung von Tellerfedern. DRAHT 22 (1971) 11, S. 760–763.

[12] Neue Kupplungen für Trabant 601 und Wartburg 353. In: Kraftfahrzeugtechnik 4/1969, S. 120–121.

[Bisch-13] Bischoff (ein Federhersteller): Technische Zeichnung (Blechabwicklung und zwei Ansichten) einer Kegelstumpffeder .

[14] In der Art einer Bandage um Finger, Arm oder Bein.

[15] Albert Albers: Grundlagen der Berechnung und Gestaltung von Maschinen. In: Waldemar Steinhilper (Hrsg.): Konstruktionselemente des Maschinenbaus. 8. Auflage. Band 1. Springer-Verlag, Berlin/Heidelberg 2012, ISBN 978-3-642-24300-4, 5.1.2.3 Nutzungsgrad, S. 206, 224.