Parameter (Statistik)

In der Statistik fassen aggregierende Parameter oder Maßzahlen die wesentlichen Eigenschaften einer Häufigkeitsverteilung, z. B. einer längeren Reihe von Messdaten, oder einer Wahrscheinlichkeitsverteilung zusammen.

Einige Parameter der deskriptiven Statistik entsprechen den Momenten von Zufallsvariablen.

Der Begriff Parameter wird auch bei Verteilungsmodellen verwendet, man spricht dann von Verteilungsparametern. Er ist dann meist eine von mehreren Größen, die zusammen mit der Verteilungsklasse die genaue Form einer Verteilung festlegen.

Lageparameter

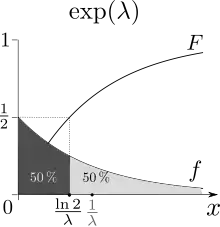Der Median (hier ${\tfrac {\ln 2}{\lambda }}$ ) teilt die Masse der Verteilung
Der Erwartungswert (hier ${\tfrac {1}{\lambda }}$ ) ist der Schwerpunkt der Verteilung

Lageparameter dienen dazu, die Lage der Gesamtheit der Stichprobenelemente beziehungsweise der Elemente der Grundgesamtheit in Bezug auf die Messskala pauschal zu beschreiben. Ein Lageparameter fasst die Gesamtheit der betrachteten Werte zu einer repräsentativen Zahl – der zentralen Tendenz – zusammen.

Definition

Sei $x_{1},\dots ,x_{n}\in \mathbb {R}$ eine Stichprobe. Eine Funktion $l:x_{1},\dots ,x_{n}\mapsto \mathbb {R}$ heißt Lagemaß, wenn sie translationsäquivariant ist:[1][2]

l(x_{1}+a,\dots ,x_{n}+a)=l(x_{1},\dots ,x_{n})+a

mit

a\in \mathbb {R}

Beispiele

In der deskriptiven Statistik nutzt man als Lageparameter einer Verteilung:

Arithmetisches Mittel: $l_{\text{arithm.}}(x_{1},\dots ,x_{n})={\frac {1}{n}}(x_{1}+\cdots +x_{n})$
empirische Quantile: Median, Quartile, Dezile, Perzentile
Modus

Für die drei zuerst genannten Lageparameter sowie Modus und Median siehe auch Mittelwert.

Bei Zufallsvariablen spricht man vom Erwartungswert.

Nach der obigen Definition sind folgende Kenngrößen keine Lagemaße:

Geometrisches Mittel: $l_{\text{geom.}}(x_{1},\dots ,x_{n})={\sqrt[{n}]{x_{1}\cdot x_{2}\dotsm x_{n}}}$
Harmonisches Mittel: $l_{\text{harm.}}(x_{1},\dots ,x_{n})={\frac {n}{{\frac {1}{x_{1}}}+\cdots +{\frac {1}{x_{n}}}}}$

Streuungsparameter

Unter einem Streuungsmaß oder Dispersionsmaß (auch Streuungsparameter) versteht man statistische Kennziffern, durch deren Ermittlung sich Aussagen über die Verteilung von zum Beispiel aus Wägungen und Zählungen stammenden Messwerten um den Mittelpunkt treffen lassen. In der Deskriptiven Statistik beschreibt man die Streuung (oder Dispersion; auch Variation) mit folgenden Maßen:

empirische Varianz, auch (mehrdeutig) Stichprobenvarianz genannt, die mittlere quadrierte Abweichung vom arithmetischen Mittel
Empirische Standardabweichung, die Wurzel aus der empirischen Varianz
Spannweite, die Differenz zwischen größter und kleinster Beobachtung (englisch range)
Mittlere absolute Abweichung vom arithmetischen Mittel
Interquartilsabstand, der die mittleren 50 % der Beobachtungen enthält (engl. interquartile range)

Konzentrationsparameter

Gestaltmaße bzw. -parameter

Einzelnachweise

Norbert Henze: Maß- und Wahrscheinlichkeitstheorie (Stochastik II). Karlsruhe 2010, S. 127.
Andreas Büchter, H.-W. Henn: Elementare Stochastik - Eine Einführung. 2. Auflage. Springer, 2007, ISBN 978-3-540-45382-6, S. 71.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Norbert Henze: Maß- und Wahrscheinlichkeitstheorie (Stochastik II). Karlsruhe 2010, S. 127.

[2] Andreas Büchter, H.-W. Henn: Elementare Stochastik - Eine Einführung. 2. Auflage. Springer, 2007, ISBN 978-3-540-45382-6, S. 71.