Hyperexponentialverteilung

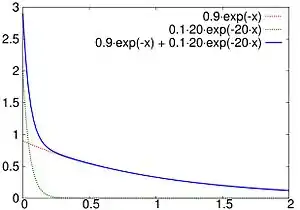
Die Hyperexponentialverteilung ist eine stetige Wahrscheinlichkeitsverteilung. Anschaulich gesprochen ist sie eine Überlagerung mehrerer Exponentialverteilungen.

Die durchgezogene, blaue Linie zeigt die Wahrscheinlichkeitsdichte einer Hyperexponentialverteilung am Beispiel p₁=0.9, p₂=0.1, λ₁=1 und λ₂=20.

Definition

Seien ${\displaystyle Y_{i}}$ (mit ${\displaystyle i=1,\dotsc ,N}$) unabhängige, exponentialverteilte Zufallsvariablen mit Raten ${\displaystyle \lambda _{i}}$ und seien ${\displaystyle p_{i}}$ Wahrscheinlichkeiten, deren Summe 1 ergibt. Dann heißt die Zufallsvariable ${\displaystyle X}$ hyperexponentialverteilt, wenn sie folgende Wahrscheinlichkeitsdichte besitzt:[1]

${\displaystyle f_{X}(x)=\sum _{i=1}^{N}p_{i}f_{Y_{i}}(x)={\begin{cases}\sum \limits _{i=1}^{N}p_{i}\lambda _{i}e^{-\lambda _{i}\,x}&x\geq 0,\\0&x<0.\end{cases}}}$

Einordnung und Bemerkungen

Bei einer Exponentialverteilung ist der Variationskoeffizient (Standardabweichung geteilt durch Erwartungswert) gleich 1. Die Bezeichnung „hyper“-exponential rührt daher, dass der Variationskoeffizient hier größer als 1 ist (sofern verschiedene ${\displaystyle \lambda _{i}}$ auftreten). Im Unterschied dazu ist er bei der Hypoexponentialverteilung kleiner als 1. Während die Exponentialverteilung das stetige Analogon zur geometrischen Verteilung ist, ist die Hyperexponentialverteilung kein Analogon zur hypergeometrischen Verteilung. Die Hyperexponentialverteilung ist ein Beispiel für eine Mischverteilung.

Als Anwendungsbeispiel kann die Auslastung eines Internetanschlusses dienen, über welchen entweder (mit Wahrscheinlichkeit ${\displaystyle p}$ und Rate ${\displaystyle \lambda _{1}}$) Internettelefonie oder (mit Wahrscheinlichkeit ${\displaystyle q}$ und Rate ${\displaystyle \lambda _{2}}$) Dateiübertragungen laufen, wobei ${\displaystyle p+q=1}$. Die Gesamtauslastung ist dann hyperexponentialverteilt.

Eine gegebene Wahrscheinlichkeitsverteilung, inklusive endlastiger Verteilungen, kann durch eine Hyperexponentialverteilung angenähert werden, indem rekursiv verschiedene Zeitskalen (${\displaystyle \lambda _{i}}$) mittels der sogenannten Prony-Methode angefittet werden.[2]

Eigenschaften

Aus d​er Linearität d​es Integrals ergibt sich:

${\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }xf(x)\,dx=\sum _{i=1}^{N}p_{i}\int _{0}^{\infty }x\lambda _{i}e^{-\lambda _{i}x}\,dx=\sum _{i=1}^{N}{\frac {p_{i}}{\lambda _{i}}}}$

und

${\displaystyle \operatorname {E} \left[X^{2}\right]=\int _{-\infty }^{\infty }x^{2}f(x)\,dx=\sum _{i=1}^{N}p_{i}\int _{0}^{\infty }x^{2}\lambda _{i}e^{-\lambda _{i}x}\,dx=\sum _{i=1}^{N}{\frac {2}{\lambda _{i}^{2}}}p_{i}\;.}$

Mit Hilfe d​es Verschiebungssatzes ergibt s​ich daraus d​ie Varianz:[3]

${\displaystyle \operatorname {Var} [X]=\operatorname {E} \left[X^{2}\right]-\operatorname {E} \left[X\right]^{2}=\sum _{i=1}^{N}{\frac {2}{\lambda _{i}^{2}}}p_{i}-\left[\sum _{i=1}^{N}{\frac {p_{i}}{\lambda _{i}}}\right]^{2}=\left[\sum _{i=1}^{N}{\frac {p_{i}}{\lambda _{i}}}\right]^{2}+\sum _{i=1}^{N}\sum _{j=1}^{N}p_{i}p_{j}\left({\frac {1}{\lambda _{i}}}-{\frac {1}{\lambda _{j}}}\right)^{2}\;.}$

Sofern nicht alle ${\displaystyle \lambda _{i}}$ gleich groß sind, ist die Standardabweichung größer als der Erwartungswert.

Die momenterzeugende Funktion i​st

${\displaystyle \operatorname {E} \left[e^{tX}\right]=\int _{-\infty }^{\infty }e^{tx}f(x)\,dx=\sum _{i=1}^{N}p_{i}\int _{0}^{\infty }e^{tx}\lambda _{i}e^{-\lambda _{i}x}\,dx=\sum _{i=1}^{N}{\frac {\lambda _{i}}{\lambda _{i}-t}}p_{i}\;.}$

Siehe auch

• Phasenverteilung

Fußnoten und Einzelnachweise

1. L. N. Singh, G. R. Dattatreya: Estimation of the Hyperexponential Density with Applications in Sensor Networks. In: International Journal of Distributed Sensor Networks. 3, Nr. 3, 2007, S. 311. doi:10.1080/15501320701259925.
2. A. Feldmann, W. Whitt: Fitting mixtures of exponentials to long-tail distributions to analyze network performance models. In: Performance Evaluation. 31, Nr. 3–4, 1998, S. 245. doi:10.1016/S0166-5316(97)00003-5.
3. H. T. Papadopolous, C. Heavey, J. Browne: Queueing Theory in Manufacturing Systems Analysis and Design. Springer, 1993, ISBN 9780412387203, S. 35.