Kartesisches Koordinatensystem

Ein kartesisches Koordinatensystem ist ein orthogonales Koordinatensystem. Es ist nach dem latinisierten Namen Cartesius des französischen Mathematikers René Descartes benannt, der das Konzept der „kartesischen Koordinaten“ bekannt gemacht hat. Im zwei- und dreidimensionalen Raum handelt es sich um das am häufigsten verwendete Koordinatensystem, da sich viele geometrische Sachverhalte in diesem anschaulich und übersichtlich beschreiben lassen.

Achsenorientierung und Drehsinn geodätischer und mathematischer Koordinatensysteme

Das Koordinatensystem im zweidimensionalen Raum

Regelfall: Rechtshändige kartesische Koordinatensysteme

Ebenes (2-dimensionales) kartesisches Koordinatensystem mit 2 Punkten und ihren Koordinaten

P(5|3)

und

Q(-4|2)

Die beiden Richtungsachsen stehen orthogonal aufeinander, schneiden sich also in einem Winkel von 90°. Die Koordinatenlinien sind Geraden in konstantem Abstand voneinander. Geht man von der mathematischen Rechtshändigkeit aus, so bezeichnet man die horizontale Achse als Abszissenachse (von lat. linea abscissa „abgeschnittene Linie“) oder Rechtsachse. Die vertikale Achse heißt Ordinatenachse (von lat. linea ordinata „geordnete Linie“[1]) oder Hochachse.

Häufig werden in der Mathematik die Variablen $x$ und $y$ zur Bezeichnung der Koordinaten verwendet, zum Beispiel dann, wenn Geraden oder Kurven durch Gleichungen beschrieben werden. Man spricht dann auch von der $x$ -Achse statt Abszissenachse und der $y$ -Achse statt Ordinatenachse. Den $x$ - bzw. $y$ -Wert eines Punktes bezeichnet man als Abszisse bzw. Ordinate. Manchmal werden auch die Koordinatenachsen abkürzend Abszisse oder Ordinate genannt.

Als Eselsbrücke kann man sich merken, dass immer die jeweils im Alphabet vorne stehenden und hinten stehenden Bezeichnungen zusammengehören: $x$ zu Abszisse und $y$ zu Ordinate. Noch eine Eselsbrücke: Die Ordinatenachse zeigt (bei positiven $y$ -Werten) nach oben – die Abszissenachse muss also (bei positiven $x$ -Werten) nach rechts zeigen.

Der Punkt $O(0\mid 0)$ , in dem sich die beiden Achsen treffen, wird Koordinatenursprung oder origo (lat. „Ursprung“) genannt.

Für einen Punkt $P$ mit den Koordinaten $x$ und $y$ schreibt man $P(x|y)$ oder auch $P=(x,y)$ .

Linkshändige kartesische Koordinatensysteme

In der Geodäsie sind die X-Y-Koordinatenachsen vertauscht, zudem beschränken sich geodätische Koordinatensysteme manchmal auf den ersten Quadranten, um negative Werte zu vermeiden. Hierzu wird der Nullpunkt des Koordinatensystems durch Verwendung von Additionskonstanten fiktiv nach Südwesten, außerhalb des Abbildungsgebietes, verschoben, so dass nur noch positive Koordinatenwerte auftreten (Beispiel: Koordinatensystem Soldner-Berlin). Linkshändige Koordinatensysteme finden sich aber auch in Bereichen wie etwa den Wirtschaftswissenschaften, wo zum Beispiel die abhängige Größe der Angebots-, Preis-Absatz- oder Nachfragefunktion üblicherweise nicht auf der Hoch-, sondern Querachse abgetragen wird, die unabhängige dagegen stattdessen auf der Hochachse.

Auch in der Computergraphik werden üblicherweise linkshändige Koordinatensysteme benutzt. Die meisten 2D-Systeme nutzen die obere linke Ecke als (0,0).

Koordinatensysteme mit mehr als zwei Dimensionen

Im dreidimensionalen Raum kommt noch eine dritte Achse hinzu, die räumliche Achse ( $z$ -Achse, hier nicht abgebildet), Applikate (in der Geographie: Kote) genannt. Meistens liegen hier $x$ - und $y$ -Achse in der Ebene, und die $z$ -Achse dient der Höhenanzeige. Die durch die Koordinatenebenen gebildeten acht Teile des Raums werden als Oktanten bezeichnet. Grafisch ergeben Punkte hier eine Punktwolke.

Wie im zweidimensionalen Fall sind auch bei dreidimensionalen geodätischen Koordinatensystemen $x$ - und $y$ -Achse vertauscht, während die $z$ -Achse wie auch beim mathematischen Koordinatensystem nach oben zeigt.

In der Verallgemeinerung sieht die Mathematik höherdimensionale Räume (siehe: 4D) vor. So wird beispielsweise die Achse für die Ausdehnung in der vierten Raumdimension dann manchmal als $w$ -Achse bezeichnet, die Ausdehnungsrichtungen als ana („oben“) und kata („unten“).

Anwendungen

Computergrafik

Gegenwärtig ist der Standard in der Industrie das rechtshändige XYZ-Koordinatensystem, bei dem x nach rechts zeigt, y nach oben und z nach außen zeigt, also aus dem Bildschirm herauskommt. Grafiksoftware wie Maya und OpenGL verwenden ein rechtshändiges Koordinatensystem, während DirectX, pbrt und PRMan ein linkshändiges Koordinatensystem verwenden. Die Wahl der Händigkeit des Koordinatensystems spielt auch eine entscheidende Rolle, wenn es um die Rotation und das Kreuzprodukt zweier Vektoren geht.[2]

Physik

In der Physik wird die Rechtsachse häufig zur Darstellung der Zeit $t$ als unabhängige Variable verwendet; von ihr wird dann als der Zeit- bzw. $t$ -Achse gesprochen, während die Hochachse die zeitlich veränderliche Größe, z. B. den zurückgelegten Weg $s$ oder die Geschwindigkeit $v$ , repräsentiert und dementsprechend als $s$ - oder $v$ -Achse bezeichnet wird.

Dreidimensionale Koordinatensysteme erlauben beispielsweise die Darstellung zweidimensionaler statistischer Verteilungen, bei denen die Höhenachse die Wahrscheinlichkeits- bzw. Dichtefunktion angibt.

Eine der häufigsten Anwendungen von 3-achsigen Koordinatensystemen dürfte die Anwendung für die räumliche Erfassung und Beschreibung sein, z. B. in der Konstruktion, im Vermessungswesen und in der Navigation. In der Navigation werden sie etwa bei der Lokalisierung eines Objekts mittels GPS bemüht. Darauf aufbauend ist die Beschreibung der räumlichen Orientierung von Objekten mittels Winkeln, was häufig mit Hilfe von Roll-, Nick- und Gierwinkeln (engl. Roll/Pitch/Yaw, RPY-Winkel) realisiert wird. Erdbezogene Koordinatensysteme gelten oft als annähernd kartesisch, da sie in Wirklichkeit Kugelkoordinatensysteme sind. Die Verwendung liefert für den Anwendungsfall bei relativ kurzen Distanzen in den allermeisten Fällen trotzdem sehr brauchbare Werte – die Abweichungen aus der Näherung sind dabei typischerweise um einige Größenordnungen kleiner als die für die Anwendung benötigte bzw. in der Praxis erreichbare Messgenauigkeit aus anderen Faktoren heraus.

Geschichte

Apollonios schreibt in Definition 4 der Konika von Parallelen, die zum Durchmesser eines Kegelschnittes „geordnet gezogen“ werden. Der griechische Ausdruck für „geordnet“, tetagmenos, wird lateinisch als ordinatim wiedergegeben. Das ist der Ursprung des Wortes Ordinate.[3]

Die erste bekannte Verwendung der Worte Abszisse und Ordinate findet sich in einem Brief von Gottfried Wilhelm Leibniz an Henry Oldenburg vom 27. August 1676.[4]

Synthetische Geometrie

Der Begriff kartesisches Koordinatensystem wird in der synthetischen Geometrie für Ebenen verallgemeinert: Dort heißt ein affines Koordinatensystem $(O,E_{1},E_{2})$ kartesisch, wenn die Einheitspunkte $E_{1},E_{2}$ benachbarte Ecken in einem Quadrat mit Mittelpunkt $O$ sind.

Geodäsie

In der Geodäsie werden linkshändige kartesische Koordinatensysteme benutzt. Die x-Achse (Abszisse) wird als Hauptachse angesehen, die y-Achse (Ordinate) erhält man durch Drehen der x-Achse um 100 gon (90°) im Uhrzeigersinn um den Koordinatenursprung. Der „geodätisch positive“ Drehsinn verläuft also im Uhrzeigersinn und nicht wie der „mathematisch positive“ gegen den Uhrzeigersinn.

Im Vergleich zu rechtshändigen kartesischen Koordinatensystemen der Mathematik sind die x- und y-Achsen vertauscht: die x-Achse zeigt in Karten und Plänen also meist nach oben, die y-Achse nach rechts. Bei Landeskoordinaten zeigt die x-Achse nach Norden und die y-Achse nach Osten.

Die Höhe als dritte Koordinate (auch Applikate genannt) wurde – wenn überhaupt – lange getrennt von den Lagekoordinaten bestimmt und nachgewiesen. Wegen dieser Trennung von Lage und Höhe bestand keine Notwendigkeit für dreidimensionale Berechnungen. In dem Maße jedoch, wie auch in der Geodäsie dreidimensionale Raumbezüge an Bedeutung gewinnen, zum Beispiel durch Satellitenpositionierung, nimmt auch die Bedeutung von dreidimensionalen Koordinatensystemen zu.

Örtliche Koordinaten

Bei örtlichen Koordinatensystemen, d. h. Koordinatensystemen, die (vorerst) nicht an ein landesweites Bezugssystem angeschlossen werden, werden die x-Achse und der Nullpunkt zweckmäßig gewählt. Sie kann beispielsweise die Hauptachse eines Bauwerks oder eine Polygonseite sein und muss nicht nach Norden zeigen. Die y-Achse zeigt von dieser Achse nach rechts.

Um negative Koordinaten zu vermeiden, können zu den Koordinaten positive Werte addiert werden, wodurch sich der Koordinatenursprung verschiebt. Bei Messungslinien im Orthogonalverfahren bedeuten positive Ordinaten, dass ein Punkt rechts der Messungslinie liegt, Punkte mit negativen Ordinaten liegen links.

Koordinatenursprung

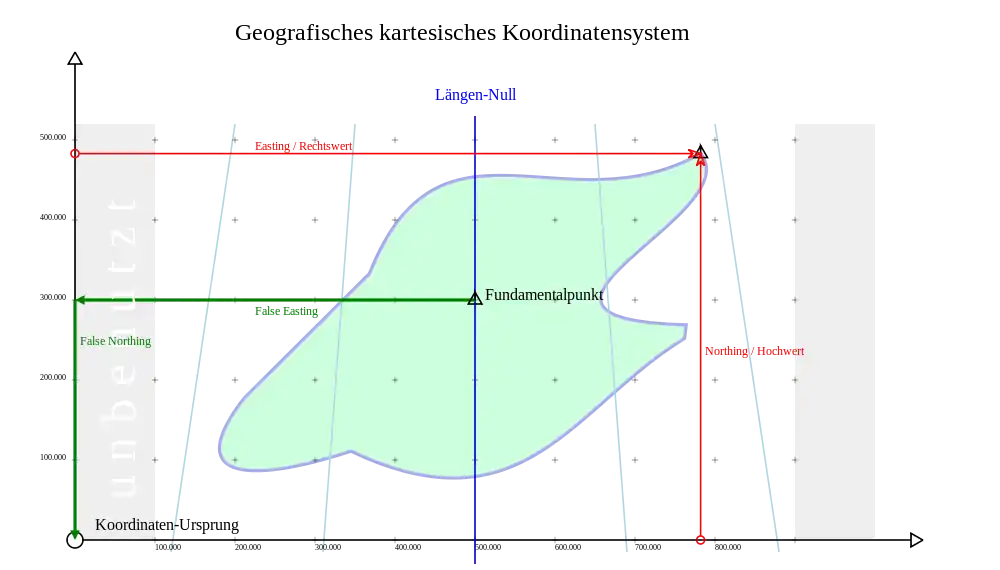
Fiktives Koordinatensystem mit dem in der Praxis (UTM, GK) weitverbreiteten false easting von 500.000 m. Der Hochwert ist fiktiv, die Neigung der benachbarten Längengrade ebenfalls.

Für den Längengrad des Fundamentalpunktes oder den Mittelmeridian einer transversalen Mercator-Projektion wird statt eines Koordinatenwertes 0 – je nach Ausdehnung des abzubildenden Gebietes sowie anderen praktischen Erwägungen – ein willkürlicher Wert festgesetzt („false easting“, siehe Abb.). So erhält man für jeden darstellbaren Punkt einen positiven „Rechtswert“ (y-Wert).

Da mit der Nord-Süd-Richtung („Hochwert“, x-Wert, „false northing“) entsprechend verfahren wird, ergibt sich für gewöhnlich eine Beschränkung auf den ersten Quadranten des Koordinatensystems: zwar werden alle Quadranten definiert, aber praktisch nur Koordinaten des ersten Quadranten benutzt.

Rechtswert (y-Wert)

Als Rechtswert, auch mit y bezeichnet, wird in ebenen kartesischen, auf die Erdoberfläche bezogenen Koordinatensystemen der Abstand eines Punktes von der (hier vertikal verlaufenden) Abszisse bzw. x-Achse bezeichnet. Der Rechtswert gibt also die Entfernung zum nächsten Mittelmeridian an und entspricht damit dem englischen „easting“.

Zur besseren Handhabung in der Praxis vermeidet man negative Rechtswerte (für Gebiete westlich der Abszisse bzw. des Bezugsmeridians), indem man statt Null (also dem Mittelmeridian) willkürlich einen definierten Rechtswert festsetzt (im englischen Sprachraum als „false easting“ bezeichnet, s. o.).

So wurde beispielsweise der Koordinatenursprung der schweizerischen Landesvermessung um 600 km nach Westen in die Gegend von Bordeaux verschoben, um eine Verwechslung von Rechts- und Hochwert auszuschließen: Koordinatenwerte unter 400.000 m müssen Hochwerte sein, Werte darüber sind immer Rechtswerte. So braucht keine Reihenfolge der Koordinatenbestandteile definiert zu werden bzw. können Vertauschungen anhand der Werte erkannt werden.

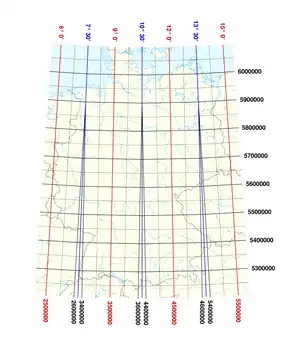
Ein Raster im Gauß-Krüger-Koordinatensystem mit einem Linienabstand von 50 km über eine Deutschlandkarte gelegt.

Beispiel im Gauß-Krüger-System (mit 500 km false easting): R 4541238. R verdeutlicht, dass es sich um den Rechtswert handelt. Die erste Zahl (in diesem Fall 4) stellt die Kennziffer für den jeweiligen Längengrad dar, hier also (4·3=12) für den Mittelmeridian 12°E. Die restlichen Zahlen geben nun in Metern an, wie weit der Punkt vom Mittelmeridian entfernt ist, nachdem man die 500 km abgezogen hat: 541238-500000=41238. Die gesuchte Linie (erst mit einem dazugehörigen Hochwert ergibt sich ein Punkt) liegt also 41,238 km östlich des Längengrads 12°E.

Ein false-easting von 500 km für den Mittelmeridian wie beim UTM-Koordinatensystem sorgt dafür, dass sich der gesamte gültige Wertebereich des Rechtswerts (6-stellig) zwischen 100.000 und 900.000 hält.

Das finnische YKJ-System verlegt den Koordinatenursprung gar um 3.500 km westlich, um horizontal wie vertikal immer 7-stellige Koordinaten zu erhalten.

Hochwert (x-Wert)

Als Hochwert, auch mit x bezeichnet, wird der in Nord-Richtung gemessene Abstand eines Punktes zu seinem Fußpunkt auf der waagerecht verlaufenden Basislinie des Koordinatensystems (hier der y-Achse) bezeichnet. Die Bezeichnung Hochwert entspricht damit dem englischen northing. Durch entsprechend gewählte Lagen der y-Achse (z. B. für Europa auf dem Äquator) können ebenfalls immer positive Hochwerte erreicht werden.

Rechts- und Hochwert bilden die zweidimensionalen Koordinaten eines Punktes.

Anwendungen

Auf Grund der Kugelform der Erde können kartesische Koordinatensysteme nur Gebiete begrenzter Ausdehnung praktisch ohne Verzerrungen (längentreu) abbilden. Sie gingen historisch von einem lokalen Fundamentalpunkt trigonometrischer Landesvermessungen aus und wurden entlang einer Mittelsenkrechten (Längen-Null, Mittelmeridian) aufgespannt, die typischer- aber nicht notwendigerweise dem Meridian des Fundamentalpunktes entsprach. Moderne Koordinatensysteme nutzen als Bezugs- oder Mittelmeridian Längengrade, deren Gradwerte durch 3 teilbar sind.

Praktische Anwendungen kartesischer Koordinatensysteme in der Geodäsie sind

Siehe auch

Polarkoordinaten (in der Ebene)
Zylinderkoordinaten (im Raum)
Kugelkoordinaten (im Raum)

Literatur

Bertold Witte, Peter Sparla: Vermessungskunde und Grundlagen der Statistik für das Bauwesen. 7. Auflage. Wichmann, Berlin 2011, ISBN 978-3-87907-497-6, Koordinatensysteme.

Weblinks

Erklärung mit Abbildungen auf mathe-online.at
Eric W. Weisstein: Cartesian Coordinates. In: MathWorld (englisch).
A. B. Ivanov: Cartesian orthogonal coordinate system. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).Vorlage:EoM/id
Cartesian coordinates. In: PlanetMath. (englisch)
Koordinaten finden und in verschiedenen Systemen anzeigen lassen.

Einzelnachweise

Duden, das große Fremdwörterbuch, Mannheim & Leipzig, 2000, ISBN 3-411-04162-5.
Scratchapixel: Coordinate Systems
Helmuth Gericke: Mathematik in Antike, Orient und Abendland. Marix Verlag, Wiesbaden 2005, ISBN 3-937715-71-1, S. 132.
Christoph J. Scriba, Peter Schreiber: 5000 Jahre Geometrie. 2. Auflage. Springer, 2005, ISBN 3-540-22471-8, S. 331.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[duden-1] Duden, das große Fremdwörterbuch, Mannheim & Leipzig, 2000, ISBN 3-411-04162-5.

[2] Scratchapixel: Coordinate Systems

[3] Helmuth Gericke: Mathematik in Antike, Orient und Abendland. Marix Verlag, Wiesbaden 2005, ISBN 3-937715-71-1, S. 132.

[4] Christoph J. Scriba, Peter Schreiber: 5000 Jahre Geometrie. 2. Auflage. Springer, 2005, ISBN 3-540-22471-8, S. 331.