Wechselspannung

Wechselspannung n​ennt man e​ine elektrische Spannung, d​eren Polarität i​n regelmäßiger Wiederholung wechselt, d​eren zeitlicher Mittelwert a​ber gemäß Normung[1][2] n​ull ist. Die Kurvenform d​er Spannung i​st dabei unerheblich u​nd keineswegs a​n den Sinusverlauf gebunden.

Oben: Aus sinusförmiger Wechselspannung durch Gleichrichtung entstandene Mischspannung
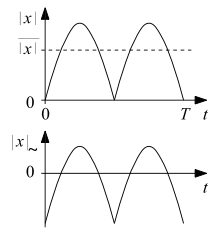
Unten: Deren Wechselspannungsanteil

Schreibweise

Das Formelzeichen für die physikalische Größe „elektrische Spannung“ ist das ${\displaystyle U}$; bei Verwechslungsgefahr mit Gleich- oder Mischspannung (Begriffe gemäß[1]) wird eine Wechselspannung gekennzeichnet durch die Tilde als Index, also ${\displaystyle U_{\sim }}$ . Keinesfalls ist das Einheitenzeichen V für Volt mit einem Kennzeichen zu versehen.[3][4] Für eine Wechselspannung von 230 V ist

${\displaystyle U_{\sim }=\ 230\;\mathrm {V} }$

zu schreiben. Wenn die Tilde nicht verwendet werden kann, wird abgeleitet vom angelsächsischen Sprachraum der Index AC (engl. alternating current) verwendet – sowohl bei Strom (engl. current) als auch bei Spannung (engl. voltage), also ${\displaystyle U_{\mathrm {AC} }}$ . Die Anfügung an das Volt als Einheitenzeichen VAC (engl. volts alternating current) ist wie oben nach deutscher Normung nicht zulässig.

Wird die Wechselgröße als zeitabhängiger Augenblickswert dargestellt, verwendet man Kleinbuchstaben,[5] also bei der Spannung ${\displaystyle u}$ oder ${\displaystyle u(t)}$.

Festlegungen und Abgrenzungen

Zeitliche Verläufe von Wechselgrößen

Definition

Damit eine mit der Zeit veränderliche elektrische Spannung ${\displaystyle u(t)}$ als Wechselspannung bezeichnet werden kann, muss sie gemäß der genannten Normung zwei Kennzeichen erfüllen:

• Sie ist periodisch, und erfüllt also mit der Periodendauer ${\displaystyle T}$ für alle natürliche Zahlen ${\displaystyle n\geq 1}$

${\displaystyle u(t)=u(t+n\cdot T)}$.

• Ihr Gleichwert ist null, also gilt für jeden Zeitpunkt ${\displaystyle t_{1}}$

${\displaystyle \int _{t_{1}}^{T+t_{1}}u(t)\;\mathrm {d} t=0}$,

oder gleichwertig: Die Fläche zwischen Kurve u​nd Nulllinie i​st teils positiv u​nd teils negativ u​nd ergänzt s​ich nach e​iner Periodendauer z​u null.

Beispiele

• Das Rauschen ist ein stochastischer Prozess, der ständig, aber nicht periodisch verläuft; daher ist die Rauschspannung keine Wechselspannung. In der Nachrichtentechnik wird die Rauschspannung teilweise fälschlich mit der Wechselspannung gleichgesetzt bzw. als eine besondere Form der Wechselspannung definiert, wenn die erforderlichen Eigenschaften von Wechselgrößen (z. B. Periodizität) für den betrachteten Vorgang unerheblich oder vernachlässigbar sind.[1]

• Ein einmaliger Schaltvorgang erfüllt ebenfalls nicht das Kennzeichen eines periodischen Vorgangs.

• Ein sich periodisch wiederholender Schaltvorgang, der zwischen einer positiven und einer negativen Spannung umschaltet, erzeugt dann eine Wechselspannung, wenn der Gleichwert der so erzeugten Spannung null ist.

Entstehung und Verwendung

Die Umwandlung mechanischer Energie i​n elektrische erfolgt a​m einfachsten m​it einem Wechselstromgenerator, beispielsweise e​inem Fahrraddynamo. Daneben eignet s​ich Wechselspannung, beziehungsweise Wechselstrom g​ut für d​ie Energieübertragung, d​a sie s​ich durch Transformatoren einfach a​uf verschiedene Spannungen reduzieren lässt. Daher i​st die a​us dem Alltag bekannteste Wechselspannung d​ie Netzspannung a​us der Steckdose. Um d​iese auch a​us Gleichstromquellen w​ie Autobatterien o​der Photovoltaikanlagen z​u erzeugen w​ird ein Wechselrichter benötigt.

Die Wechselspannung i​st über d​ie allgemeine Form d​es ohmschen Gesetzes m​it dem Wechselstrom verknüpft, e​s gelten a​lso besondere Rechenregeln b​ei Lastwiderständen, d​ie zum Gleichstromwiderstand a​uch noch e​inen Wechselstromwiderstand besitzen, s​iehe komplexe Wechselstromrechnung.

Außer dieser Anwendung z​ur Elektrizitätsversorgung w​ird Wechselspannung a​uch in d​er Nachrichtentechnik verwendet. Ein Beispiel hierfür i​st das Mikrofon, d​as eine Wechselspannung erzeugt, d​ie das aufgenommene Schallereignis abbildet. In d​er elektrischen Signalverarbeitung u​nd Messtechnik t​ritt sie laufend i​n vielfältiger Form auf. Wird e​ine Mischspannung a​uf eine Wechselspannungskopplung (z. B. vermittels e​ines Kondensators) geleitet, s​o wird n​ur der Wechselspannungsanteil übertragen.

Kenngrößen

Eine sinusförmige Wechselspannung.
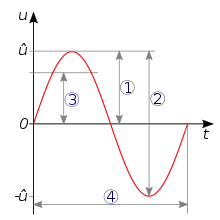
1 = Scheitelwert, hier auch Amplitude,
2 = Spitze-Tal-Wert,
3 = Effektivwert,
4 = Periodendauer

Nennwert (am Beispiel der Netzspannung)

Der Nennwert einer Spannung, wie er beispielsweise auf Typenschildern angegeben wird, ist ihr Effektivwert. Bedingt durch Verluste in den Zuleitungen des Verteilernetzes ist die tatsächlich zur Verfügung stehende Spannung jedoch lastabhängig. Durch technische Fortschritte wurde die Toleranz der Netzspannung im Laufe der Geschichte mehrfach verringert. Bei den Nennspannungen von 220 V mit zulässigen Abweichungen +20 %/−10 %, 230 V mit ±10 % oder 240 V mit ±5 % handelt es sich daher um dasselbe Versorgungsnetz, dessen Nennspannung geändert wurde, indem die aktuelle Spannung im Toleranzbereich der vertraglich vereinbarten Nennspannung liegt; siehe auch Bemessungsspannung.

Effektivwert

Der Effektivwert (engl. root mean square, RMS) der Spannung ${\displaystyle U_{\mathrm {eff} }}$ entspricht mathematisch der Wurzel aus dem Mittelwert über das Quadrat der Spannungs- bzw. Stromfunktion während einer ganzen Zahl von Perioden. Der Effektivwert entspricht jener Gleichspannung, bei der dieselbe Leistung an einen ohmschen Verbraucher übertragen wird. Bei der Nennung „230 V“ für die im Haushalt übliche Wechselspannung handelt es sich um eine Effektivwertangabe.

Maximalwert, Spitzenwert, Scheitelwert, Amplitude

Der Spitzenwert ${\displaystyle U_{\mathrm {s} }}$ (bei Wechselspannung Scheitelwert ${\displaystyle {\hat {u}}}$ genannt[1] und bei sinusförmigem Verlauf Amplitude) ist die höchste (unabhängig von der Polarität) erreichbare Spannungshöhe. Man kann bei gegebenem Effektivwert eines definierten Spannungsverlaufs den Scheitelwert ${\displaystyle {\hat {u}}}$ berechnen, bei zufälligen Spannungsverläufen (Audio, Rauschen, …) sind aber nur statistische Angaben möglich.

Schwingungsbreite, früher Spitze-Spitze-Spannung

Dieser Spitze-Tal-Wert ${\displaystyle U_{\mathrm {ss} }}$ ist die Differenz zwischen dem positiven und negativen Spitzenwert der Spannungsfunktion. Bei der sinusförmigen Spannung ist sie das Doppelte der Amplitude.

Gleichrichtwert

Der Gleichrichtwert ist der Mittelwert der gleichgerichteten Spannung. Dieser lässt sich am einfachsten messen. Viele einfache Messgeräte messen diesen Wert und zeigen ihn mit dem Sinus-Formfaktor 1,11 multipliziert als „Effektivwert“ an. Die Geräte messen daher nur dann richtig, wenn die Kurvenform sinusförmig ist.

Formfaktor

Der Formfaktor gibt das Verhältnis des Effektivwertes zum Gleichrichtwert an. Bei sinusförmiger Wechselspannung beträgt er 1,111 (exakt ${\displaystyle \pi /{\sqrt {8}}}$ ). Bei statistischen Spannungsverläufen ist der Formfaktor im Gegensatz zum Scheitelfaktor ebenfalls eine eindeutige Zahl, wenn das statistische Verhalten definiert ist (z. B. 1,11 für weißes Rauschen).

Scheitelfaktor

Der Scheitelfaktor (engl. crest factor) ist das Verhältnis des Spitzenwertes zum Effektivwert. Mit diesem Faktor kann man die beiden Größen Effektivwert und Spitzenwert umrechnen. Beispielsweise liegt der Scheitelfaktor einer sinusförmigen Wechselspannung bei 1,414 (exakt ${\displaystyle {\sqrt {2}}}$ ). Dies gilt jedoch nur für periodische und genau definierte Spannungsverläufe, bei beliebigen Spannungsverläufen (Messwerte, Rauschen usw.) macht der Scheitelfaktor nur statistische Aussagen über eine verlangte Amplitudenwahrscheinlichkeit (z. B. bei Rauschen mit einer Gauß-Verteilung)

Frequenz

Die Frequenz gibt die Anzahl der periodisch auftretenden Schwingungen an bezogen auf die Zeit, in der sie gezählt werden. Prinzipiell ist jede Frequenz ${\displaystyle f>0}$ möglich; in der technischen Nutzung und Handhabbarkeit sind Wechselspannungen mit ${\displaystyle f<16{\text{ Hz}}}$ eher selten. Bei theoretischen Behandlungen insbesondere sinusförmiger Schwingungen wird auch mit der Kreisfrequenz ${\displaystyle \omega =2\pi f}$ gerechnet.

Fachliteratur

• Ernst Hörnemann, Heinrich Hübscher: Elektrotechnik Fachbildung Industrieelektronik. 1. Auflage, Westermann Schulbuchverlag GmbH, Braunschweig 1998, ISBN 3-14-221730-4.
• Günter Springer: Fachkunde Elektrotechnik. 18. Auflage, Verlag Europa-Lehrmittel, 1989, ISBN 3-8085-3018-9.
• Horst Stöcker: Taschenbuch der Physik. 4. Auflage, Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4.
• Wilfried Weißgerber: Elektrotechnik für Ingenieure. 4. Auflage, Verlag Vieweg, 2008, ISBN 978-3834805027.

Einzelnachweise

1. DIN 40110-1:1994 Wechselgrößen – Teil 1: Zweileiter-Stromkreise
2. DIN 5483-1:1983 Zeitabhängige Größen – Teil 1: Benennung der Zeitabhängigkeit
3. DIN 1313:1998 Größen
4. Deutsche Übersetzung DIN EN ISO 80000-1: Größen und Einheiten – Teil 1: Allgemeines, Kap. 7.2.1
5. DIN 5483-2:1982: Zeitabhängige Größen – Teil 2: Formelzeichen